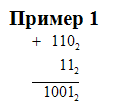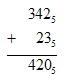Как найти сумму чисел в пятеричной системе

Арифметические
операции в рассматриваемых позиционных
системах счисления выполняются по
законам, известным из десятичной
арифметики. Двоичная система счисления
имеет основание 2, и для записи чисел
используются всего две цифры 0 и 1 в
отличие от десяти цифр десятичной
системы счисления.

Рассмотрим
сложение одноразрядных чисел: 0+0=0, 0+1=1,
1+0=0. Эти равенства справедливы как для
двоичной системы, так и для десятичной
системы. Чему же равно 1+1? В десятичной
системе это 2. Но в двоичной системе нет
цифры 2! Известно, что при десятичном
сложении 9+1 происходит перенос 1 в старший
разряд, так как старше 9 цифры нет. То
есть 9+1=10. В двоичной системе старшей
цифрой является 1. Следовательно, в
двоичной системе 1+1=10, так как при сложении
двух единиц происходит переполнение
разряда и производится перенос в старший
разряд. Переполнение разряда наступает
тогда, когда значение числа в нем
становится равным или большим основания.
Для двоичной системы это число равно 2
(10₂=2₁₀).

Продолжая
добавлять единицы, заметим: 10₂+1=11₂,
11₂+1=100₂
— произошла «цепная реакция», когда
перенос единицы в один разряд вызывает
перенос в следующий разряд.

Сложение
многоразрядных
чисел происходит по этим же правилам с
учетом возможности переносов из младших
разрядов в старшие.

Вычитание
многоразрядных
двоичных чисел производится с учетом
возможных заёмов
из старших разрядов.

Действия
умножения и деления чисел в двоичной
арифметике можно выполнять по общепринятым
для позиционных систем правилам.

В
основе правил арифметики любой позиционной
системы лежат таблицы
сложения и умножения одноразрядных
чисел.

Таблицы,
аналогичные таблицам арифметических
операций в двоичной системе счисления
(см. п.1.3), составляются для любой
позиционной системы счисления. Пользуясь
такими таблицами, можно выполнять
действия над многозначными числами.

Пример
4.Выполнить
действия в пятеричной системе счисления:
342₅+23₅;
213₅^.5₅.
     Решение:
     Составим
таблицы сложения и умножения для
пятеричной системы счисления:

Рассуждаем
так: два плюс три равно 10 (по таблице); 0
пишем, 1 — в уме. Четыре плюс два равно 11
(по таблице), да еще один, 12. 2 пишем, 1 — в
уме. Три да один равно 4 (по таблице).
Результат — 420.

Рассуждаем
так: трижды три — 14 (по таблице); 4 пишем,
один — в уме. Трижды один дает 3, да плюс
один, — пишем 4. Дважды три (по таблице) —
11; 1 пишем, 1 переносим влево. Окончательный
результат — 1144.
     Если
числа, участвующие в выражении,
представлены в разных системах, нужно
сначала привести их к одному основанию.

Пример
5.Сложить
два числа: 17₈
и 17₁₆.
     Решение:
     Приведем
число 17₁₆
к основанию 8 посредством двоичной
системы (пробелами условно обозначено
деление на тетрады и триады):
17₁₆=10111₂=10111₂=27₈.
     Выполним
сложение в восьмеричной системе:

     

     Таким
образом, арифметические действия в
позиционных системах счисления
выполняются по общим правилам. Необходимо
только помнить, что перенос в следующий
разряд при сложении и заем из старшего
разряда при вычитании определяются
величиной основания системы счисления.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Объяснение:

а) Переведем 221 в 10-ю систему:

221(5)=2•5^2 +2•5^1 +1•5^0=50+10+1=61(10)

Переведем 104 в 10-ю систему:

104(5)=1•5^2 +0•5^1 +4•5^0=25+0+4=29(10)

Сумма в 10-й системе:

61+29=90

Переведем 90 в 5-ю систему:

90/5=18 остаток 0

18/5=3 остаток 3

3/5=0 остаток 3

90(10)=330(5)

Сумма в 5-й системе:

221+104=330

б) Перевод 432 в 10-ю систему:

432(5)=4•5^2 +3•5^1 +2•5^0=100+15+2=117(10)

Перевод 114 в 10-ю систему:

114(5)=1•5^2 +1•5^1 +4•5^0=25+5+4=34(10)

Сумма в 10-й системе:

117+34=151

Перевод 151 в 5-ю систему:

151/5=30 остаток 1

30/5=6 остаток 0

6/5=1 остаток 1

1/5=0 остаток 1

151(10)=1101(5)

Сумма в 5-й системе:

432+114=1101

Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.

Вам необходимо определиться сколько чисел вам необходимо посчитать и выбрать это количество в графе количество чисел.

Далее Вам необходимо ввести каждое число и выбрать его систему счисления. Если в указанном списке Вы не нашли нужной СС, то выберите пункт другая и введите числом основание вашей системы счисления.

После ввода всех чисел и выбора арифметических операций нажмите кнопку рассчитать.