Как найти сумму числовых рядов - Исправление недочетов и поиск решений вместе с Examum.ru

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $.

Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

Источник

Нахождение суммы числового ряда. Первая часть.

В теме про основные понятия числовых рядов было указано определение суммы ряда. Вот оно:

Если существует конечный предел $S=lim_{ntoinfty}S_n$, то его называют суммой ряда $sumlimits_{n=1}^{infty}u_n$ и сам ряд именуют сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд называют расходящимся.

Если понятие «частичная сумма» вызывает вопросы, то советую посмотреть раздел про частичную сумму ряда, обратив внимание на пример №4. В этом примере подробно раскрывается суть частичной суммы и остатка.

В данной теме нас будет интересовать вопрос нахождения сумм числовых рядов по определению. Определение суммы ряда опирается на значение $lim_{ntoinfty}S_n$, поэтому для нахождения суммы нам нужно выполнить два шага:

Составить n-ю частичную сумму $S_n$;
Найти $lim_{ntoinfty}S_n$ (если он существует).

Если конечный $lim_{ntoinfty}S_n$ существует, то его значение и будет суммой рассматриваемого ряда, а сам ряд будет именоваться сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд будет расходиться. Есть несколько стандартных приёмов, которые применяются для нахождения суммы числовых рядов. Например, для нахождения суммы ряда, общий член которого имеет вид рациональной дроби $u_n=frac{P(n)}{Q(n)}$, вполне подходит такой алгоритм:

Разложить дробь $frac{P(n)}{Q(n)}$ на элементарные дроби (процедура разложения описана тут).
Записать выражение для частичной суммы $S_n$, используя результаты предыдущего пункта.
Перегруппировать слагаемые в выражении для $S_n$, приведя их к удобному для сокращения виду.
Используя результат предыдущего пункта, найти $lim_{ntoinfty}S_n$.

Для нахождения суммы ряда нередко удобно использовать и такое свойство:

Пусть общий член ряда $sumlimits_{n=1}^{infty}u_n$ можно представить в виде $u_n=b_{n+1}-b_n$. Если существует конечный предел $lim_{ntoinfty}b_n=b$, то ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом частичная сумма ряда равна $S_{n}=b_{n+1}-b_1$, а сумма ряда $S=b-b_1$.

Доказательство этого свойства может быть интересно не всем читателям, поэтому я скрою его под примечание.

Доказательство свойства: показатьскрыть

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Пример №1

Найти сумму ряда $sumlimits_{n=1}^{infty}(-1)^{n+1}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=(-1)^{n+1}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=\=(-1)^2+(-1)^3+(-1)^4+(-1)^5+ldots+(-1)^{n+1}=1-1+1-1+ldots+(-1)^n.
$$

Вопрос в следующем: чему равна эта сумма? Если в частичных суммах мы станем брать чётное количество слагаемых, они попарно сократятся:

begin{aligned}
& S_2=1-1=0;\
& S_4=1-1+1-1=0;\
& S_6=1-1+1-1+1-1=0;\
& S_8=1-1+1-1+1-1+1-1=0.
end{aligned}

Итак, частичная сумма, содержащая чётное количество слагаемых, равна 0. Т.е. если $n$ – чётное число, то $S_n=0$. Фразу «n – чётное число» можно записать так: $n=2k$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1=2$, $n=2cdot 2=4$, $n=2cdot 3=6$, $n=2cdot 4=8$ и так далее. Итак, $S_{2k}=0$.

Если мы станем брать нечётное количество слагаемых (1, 3, 5 и т.д.), то сумма станет равна 1:

begin{aligned}
& S_1=1;\
& S_3=1-1+1=1;\
& S_5=1-1+1-1+1=1;\
& S_7=1-1+1-1+1-1+1=1.
end{aligned}

Таким образом, если $n$ – нечётное число, то $S_n=1$. Фразу «n – нечётное число» можно записать так: $n=2k-1$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1-1=1$, $n=2cdot 2-1=3$, $n=2cdot 3-1=5$, $n=2cdot 4-1=7$ и так далее. Итак, $S_{2k-1}=1$.

Формально равенство $S_{2k-1}=1$ можно доказать с помощью формулы $S_{2k}=S_{2k-1}+u_{2k}$. Так как $S_{2k}=0$, то $S_{2k-1}+u_{2k}=0$, т.е. $S_{2k-1}=-u_{2k}$. Так как $u_{2k}=(-1)^{2k+1}=left((-1)^2right)^kcdot (-1)^1=-1$, то $S_{2k-1}=-(-1)=1$.

Возникает вопрос: как быть с пределом $lim_{ntoinfty}S_n$? Ведь если $n$ – чётное число, т.е. $n=2k$, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k}=lim_{ktoinfty}0=0.
$$

С другой стороны, если $n$ – нечётное число, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k-1}=lim_{ktoinfty}1=1.
$$

Что мы получили? А получили мы следующее: последовательность частичных сумм ${S_n}$ имеет две подпоследовательности: ${S_{2k-1}}$ и ${S_{2k}}$, пределы которых различны. Следовательно, последовательность ${S_n}$ не имеет предела. Вывод: ряд не имеет суммы, т.е. расходится.

Здесь стоит обратить внимание вот на что: следует различать случаи, когда предел равен бесконечности (см. следующий пример №2), и когда предела попросту не существует. Хотя и в том и в другом случаях ряд будет расходиться.

Ответ: ряд расходится.

Пример №2

Найти сумму ряда $sumlimits_{n=1}^{infty}(3n+1)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=3n+1$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=4+7+10+13+ldots+3n+1.
$$

Эту сумму можно записать в более коротком виде. Дело в том, что последовательность 4, 7, 10, 13 и т.д. есть арифметическая прогрессия, первый член которой равен 4, а разность равна 3. Сумма первых n членов этой прогрессии такова:

$$
4+7+10+13+ldots+3n+1=frac{4+3n+1}{2}cdot n=frac{3n+5}{2}cdot{n}.
$$

Итак, $S_n=frac{3n+5}{2}cdot n$. Найдем $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{3n+5}{2}cdot nright)=+infty.
$$

Так как $lim_{ntoinfty}S_n=+infty$, то ряд расходится.

Если немного выйти за рамки данной темы, то стоит отметить, что расходимость этого ряда легко доказывается с помощью необходимого признака сходимости.

Ответ: ряд расходится.

Пример №3

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{2}{(2n+1)(2n+3)}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2}{(2n+1)(2n+3)}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}.
$$

Почему я пишу именно $frac{2}{3cdot 5}$, а не $frac{2}{15}$, будет ясно из дальнейшего повествования. Однако запись частичной суммы ни на йоту не приблизила нас к цели. Нам ведь нужно найти $lim_{ntoinfty}S_n$, но если мы просто запишем:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}right),
$$

то эта запись, совершенно верная по форме, ничего нам не даст по сути. Чтобы найти предел, выражение частичной суммы предварительно нужно упростить.

Для этого есть стандартное преобразование, состоящее в разложении дроби $frac{2}{(2n+1)(2n+3)}$, которая представляет общий член ряда, на элементарные дроби. Вопросу разложения рациональных дробей на элементарные посвящена отдельная тема (см., например, пример №3 на этой странице). Раскладывая дробь $frac{2}{(2n+1)(2n+3)}$ на элементарные дроби, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}=frac{Acdot(2n+3)+Bcdot(2n+1)}{(2n+1)(2n+3)}.
$$

Приравниваем числители дробей в левой и правой частях полученного равенства:

$$
2=Acdot(2n+3)+Bcdot(2n+1).
$$

Чтобы найти значения $A$ и $B$ есть два пути. Можно раскрыть скобки и перегруппировать слагаемые, а можно просто подставить вместо $n$ некие подходящие значения. Сугубо для разнообразия в этом примере пойдём первым путём, а следующем – будем подставлять частные значения $n$. Раскрывая скобки и перегруппировывая слагаемые, получим:

$$
2=2An+3A+2Bn+B;\
2=(2A+2B)n+3A+B.
$$

В левой части равенства перед $n$ стоит ноль. Если угодно, левую часть равенства для наглядности можно представить как $0cdot n+ 2$. Так как в левой части равенства перед $n$ стоит ноль, а в правой части равества перед $n$ стоит $2A+2B$, то имеем первое уравнение: $2A+2B=0$. Сразу разделим обе части этого уравнения на 2, получив после этого $A+B=0$.

Так как в левой части равенства свободный член равен 2, а в правой части равенства свободный член равен $3A+B$, то $3A+B=2$. Итак, имеем систему:

$$
left{begin{aligned}
& A+B=0;\
& 3A+B=2.
end{aligned}right.
$$

Можно решать эту систему методом Крамера, методом Гаусса или с помощью обратной матрицы. Однако проще всего банально выразить из первого уравнения $A=-B$ и подставить во второе:

$$
3cdot (-B)+B=2;; -2B=2; ; B=-1.
$$

Так как $B=-1$, то $A=-B=1$. Подставляя найденные значения $A=1$ и $B=-1$ в формулу $frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}$, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{1}{2n+1}+frac{-1}{2n+3}=frac{1}{2n+1}-frac{1}{2n+3}.
$$

Итак, $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Используем полученное разложение для того, чтобы упростить формулу частичной суммы ряда. Покажу сначала решение стандартным путём, принятым в большинстве решебников и методичек.

Первый способ упрощения формулы для частичной суммы.

Мы получили разложение общего члена ряда на две дроби: $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:

begin{aligned}
& u_1=frac{2}{3cdot 5}=frac{1}{3}-frac{1}{5};\
& u_2=frac{2}{5cdot 7}=frac{1}{5}-frac{1}{7};\
& u_3=frac{2}{7cdot 9}=frac{1}{7}-frac{1}{9};\
& u_4=frac{2}{9cdot 11}=frac{1}{9}-frac{1}{11}.
end{aligned}

Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}.
$$

Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.

Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны «увидеть» (как любят писать некоторые авторы – «легко увидеть»), что слагаемые сокращаются. А если мы «увидим» не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.

Формулу $S_n=frac{1}{3}-frac{1}{2n+3}$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.

Доказательство формулы $S_n=frac{1}{3}-frac{1}{2n+3}$: показатьскрыть

В стандартном курсе высшей математики обычно довольствуются «вычёркиванием» сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac{1}{3}-frac{1}{2n+3}$. Найдём значение $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Вывод: заданный ряд сходится и сумма его $S=frac{1}{3}$.

Второй способ упрощения формулы для частичной суммы.

Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:

$$
u_n=frac{1}{2n+1}-frac{1}{2n+3}
=frac{-1}{2n+3}-frac{-1}{2n+1}
$$

Обозначим $b_n=frac{-1}{2n+1}$, тогда $b_{n+1}=frac{-1}{2(n+1)+1}=frac{-1}{2n+3}$. Таким образом, $u_{n}=b_{n+1}-b_{n}$. При этом $lim_{ntoinfty}b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом его сумма равна $S=0-b_1=frac{1}{3}$. Если есть необходимость, можно записать и частичную сумму ряда:

$$
S_n
=b_{n+1}-b_1
=frac{-1}{2n+3}-left(-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Третий способ упрощения формулы для частичной суммы.

Честно говоря, я сам предпочитаю большей частью именно этот способ Давайте запишем частичную сумму в сокращённом варианте:

$$
S_n=sumlimits_{k=1}^{n}u_k=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}.
$$

Мы получили ранее, что $u_k=frac{1}{2k+1}-frac{1}{2k+3}$, поэтому:

$$
S_n=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right).
$$

Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac{1}{2k+1}$, а уж затем переходить к слагаемым вида $frac{1}{2k+3}$. Это означает, что частичную сумму мы представим в таком виде:

$$
S_n
=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}=\
=frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+1}-left(frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+3}right).
$$

Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:

$$
S_n=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}.
$$

Теперь преобразуем выражения $frac{1}{2k+1}$ и $frac{1}{2k+3}$ к одному виду. Приведём, например, дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Выражение в знаменателе дроби $frac{1}{2k+3}$ я представлю в таком виде:

$$
frac{1}{2k+3}=frac{1}{2k+2+1}=frac{1}{2(k+1)+1}.
$$

И сумму $sumlimits_{k=1}^{n}frac{1}{2k+3}$ теперь можно записать так:

$$
sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Если равенство $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.

Как мы получили преобразованную сумму? показатьскрыть

Таким образом, частичную сумму можно представить в следующем виде:

$$
S_n=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Заметьте, что суммы $sumlimits_{k=1}^{n}frac{1}{2k+1}$ и $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.

Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac{1}{2k+1}=frac{1}{2n+3}$. Прибавляя и вычитая из первой суммы $frac{1}{2n+3}$, получим:

$$
sumlimits_{k=1}^{n}frac{1}{2k+1}
=sumlimits_{k=1}^{n}frac{1}{2k+1}+frac{1}{2n+3}-frac{1}{2n+3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}
$$

Для второй суммы $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac{1}{2k+1}=frac{1}{3}$. Прибавляя и вычитая $frac{1}{3}$, получим:

$$
sumlimits_{k=2}^{n+1}frac{1}{2k+1}
=sumlimits_{k=2}^{n+1}frac{1}{2k+1}+frac{1}{3}-frac{1}{3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}
$$

С учётом полученных результатов, выражение для $S_n$ примет такой вид:

$$
S_n
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:

$$
S_n=sumlimits_{k=1}^{n}u_k
=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}
=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=\

=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}
=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}=\

=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Напомню, что мы приводили дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac{1}{2k+1}$ в виде $frac{1}{2k+3}$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.

Как найти $S_n$, если приводить к виду иной дроби? показатьскрыть

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Находим предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Заданный ряд сходится и сумма его $S=frac{1}{3}$.

Ответ: $S=frac{1}{3}$.

Продолжение темы нахождения суммы ряда будет рассмотрено во второй и третьей частях.

Источник

Вычисление
суммы сходящегося числового ряда.

Прежде чем приступить к решению задач
дадим основные определения.

Определение 1.Пусть—
последовательность действительных
чисел. Выражение вида:

называется числовым рядом.

Сумму
первых
слагаемых называют
-ой
частичной суммойряда и обозначают:

К примеру,

Частичные суммы ряда
образуют бесконечную числовую
последовательность.

Выражение само по себе определенного смысла не
имеет, потому что действие сложения
производится над конечным числом
слагаемых. Этот смысл выражению предстоит
приписать нам самим.

Введем понятие суммы ряда.

Определение 2.Суммойчислового
ряданазывается предел последовательности
частичных сумм ряда,
если этот предел существует и конечен:

Числовой ряд при этом называется
сходящимся.

В противном случае, т.е. если
равен бесконечности или не существует,
то

ряд называется расходящимся.

Определение 3.Пусть дан ряд.

Ряд
,
полученный из исходного отбрасываниемпервых членов называется
-м
остатком ряда.

Можно доказать, что если
,
то ряд сходится (существует конечная
сумма)
и наоборот: остатоксходящегося
ряда стремится к нулю с увеличением
номера.

Основной целью теории числовых
рядов является установление факта
сходимости или расходимости тех или
иных рядов и вычисление суммы сходящихся
рядов. При этом найти точное значение
суммы ряда удается далеко не всегда. В
этом случае используются методы
приближенного вычисления суммы
ряда.
Существует довольно много
приемов, позволяющих устанавливать
сходимость или расходимость рядов.
Такие приемы называются признаками
сходимости. К рассмотрению некоторых
из них мы и приступаем.

Теорема (необходимый признак
сходимости числового ряда).

Если ряд
сходится,
то его общий член стремиться к нулю,
т.е.

Из необходимого признака следует,
что если
-ый
член ряда не стремиться к нулю, то ряд
расходиться. Именно это утверждение
удобно использовать для решения задач.

Отметим, что необходимый признак
не является достаточным, т.е. если
,
то о сходимости ряда ничего сказать
нельзя: он может быть как сходящимся,
так и расходящимся.

Задача №1.Исследовать ряд на
сходимость.

Решение.

Используя необходимый признак сходимости,
делаем вывод о том, что ряд расходиться,
поскольку
-ый
член ряда не стремиться к нулю.

Ответ: ряд
расходится.

Задача №2.Исследовать ряд на
сходимость.

Решение.Общий член ряда

Следовательно, ряд расходиться по
необходимому признаку. Здесь для
вычислений использовали первый
замечательный предел:
.

Ответ: ряд расходится.

Задача №3.Исследовать ряд на
сходимость.

Решение.

не существует. Ряд расходится по
необходимому признаку.

Ответ: ряд расходится.

Приведем пример ряда, для которого
необходимый признак не дает ответа о
его сходимости:

Задача №4. Исследовать ряд на
сходимость.

Решение.

Необходимый признак для данного ряда
выполняется, поэтому он может быть или
сходящимся, или расходящимся. Докажем,
что этот ряд на самом деле расходится.
Оценим частичную сумму ряда
снизу:

Таким образом,

и.

Тогда по определению суммы ряда имеем:

Ответ: ряд расходится.

Задача №5.Исследовать ряд на
сходимость.

Решение.Воспользуемся необходимым
признаком и найдем предел-го
члена ряда:

Ответ: ряд расходится.

В предыдущих задачах нашей целью
было установить сам факт существования
суммы ряда. Рассмотрим задачи, в которых
удается вычислить точное значение суммы
ряда.

Пусть дан числовой ряд
,
составленный из членов геометрической
прогрессии. Здесь—
первый член прогрессии,—
знаменатель прогрессии. Если знаменатель
прогрессии удовлетворяет условию,
то прогрессия называется бесконечно
убывающей, а ряд, составленный из членов
такой прогрессии, сходится, причем
сумма ряда равна:

Задача №6.Найти сумму ряда.

Решение.

Этот ряд составлен из членов бесконечно
убывающей геометрической прогрессии,
.

Сумма ряда равна:

Ответ:
.

Задача №7. Найти сумму ряда.

Решение.

Здесь первый член геометрической
прогрессии
,
знаменатель.
Тогда.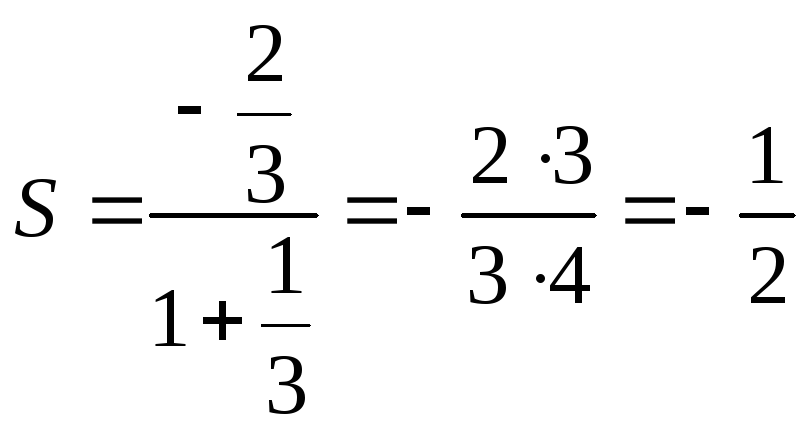

Ответ:
.

Задача №8.Найти сумму ряда.

Решение.

. Для этого ряда
.

Находим сумму:

Ответ:
.

Задача №9. Найти сумму ряда.

Решение.Для того чтобы найти сумму
этого ряда, представим общий член ряда
в виде суммы дробей:

Найдем неизвестные коэффициенты
следующим образом:

отсюда

При
из
последнего равенства получаем.

При
.

Таким образом

Найдем
-ую
частичную сумму ряда:

После сокращения противоположных
слагаемых получим

откуда

Ответ:
.

Соседние файлы в папке Ряды

Источник

Содержание:

Понятие суммы ряда
Вычисление суммы ряда почленным интегрированием
Вычисление суммы ряда почленным дифференцированием

Понятие суммы ряда

Постановка задачи. Найти сумму ряда

где — целые числа.

План решения. Суммой ряда называется предел последовательности его частичных сумм , т.е.

где

1. По условию задачи

Если корни знаменателя различаются на целое число, т.е. где — натуральное число, то члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

2. Разлагаем общий член ряда на элементарные дроби:

и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.

3. Находим -ю частичную сумму ряда:

сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле (1)

и записываем ответ.

Пример:

Найти сумму ряда

Решение:

1. Корни знаменателя и различаются на целое число, т.е. Следовательно, члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

2. Разлагаем общий член ряда на элементарные дроби

и выписываем несколько членов ряда:

3. Сокращая все слагаемые, какие возможно, находим -ю частичную сумму ряда:

4. Вычисляем сумму ряда по формуле (1):

Ответ:

Возможно вам будут полезны данные страницы:

Вычисление суммы ряда почленным интегрированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится. Если , ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами

2. Делаем в исходном ряде замену , получим степенной ряд

с областью сходимости .

3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то сумма ряда непрерывна в этой точке (справа). Следовательно,

6. Вычисляем интеграл, делаем замену на и записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:

и вычисляем сумму каждого ряда почленным интегрированием.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

В граничных точках при ряд расходится, при ряд сходится условно.

Следовательно, данный ряд сходится при всех .

2. Сделаем замену Получим геометрический ряд (1) с областью сходимости

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех .

6. Заменяя на , получаем при

Ответ.

Вычисление суммы ряда почленным дифференцированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем

6. Вычисляем производную и делаем замену на . Записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то вычисляем сумму трех рядов, причем при вычислении суммы ряда

применяем теорему о почленном дифференцировании степенного ряда дважды.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством . Отсюда . В граничных точках ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале .