Найти сумму целых решений неравенства:|x+2|*(x²+3x-4)<0
Решение:
Рассмотрим первый множитель произведения левой части неравенства
|x+2|≥0 для всех значений х∈R
х+2=0 при х=-2
Следовательно при х=-2 неравенство не имеет смысла.
Поэтому можно записать, что
x² + 3x — 4 < 0
Решим неравенство по методу интервалов. Разложим квадратный трехчлен на множителя решив квадратное уравнение
x² + 3x — 4 = 0
D =3²-4*(-4) = 9 + 16 = 25
х₁=(-3-5)/2=-4
х₂=(-3+5)/2=1
Поэтому x² + 3x — 4 =(х+4)(x-1)
Заново запишем неравенство
(х + 4)(x — 1) < 0
На числовой прямой отобразим точки где левая часть неравенства меняет свои знаки. По методу подстановки определим знаки левой части неравенства и отобразим их на числовой прямой. Например при х=0 (х + 4)(x — 1)=4*(-1)=-4<0
+ 0 — 0 +
———————!————————!—————
-4 1
Следовательно x² + 3x — 4 < 0 при х∈(-4;1)
Учитывая что х≠-2 можно записать что исходное неравенство
|x+2|*(x²+3x-4)<0 истинно для всех значений х∈(-4;-2)U(-2;1).
Целых решений неравенства три: -3; -1; 0.
Сумма целых решений неравенства равна 0 — 1 — 3 = -4
Ответ:-4
Отметим множество решений неравенства на числовой прямой и запишем ответ в виде числового промежутка.
Алгебраические неравенства.
Квадратные неравенства. Рациональные неравенства высших степеней.
Дробно-рациональные неравенства.
Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.
- I. Квадратные неравенства, то есть неравенства вида
ax2 + bx + c > 0 (< 0), a ≠ 0.
Будем считать, что a>0. Если это не так, то умножив обе части неравенства на -1 и изменив знак неравенства на противоположный, получим желаемое.
Чтобы решить неравенство можно:
- Квадратный трехчлен разложить на множители, то есть неравенство записать в виде
a (x — x1) (x — x2) > 0 (< 0).
- Корни многочлена нанести на числовую ось. Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
- Определить знак a (x — x1) (x — x2) в каждом промежутке и записать ответ.
Если квадратный трехчлен не имеет корней, то при D<0 и a>0 квадратный трехчлен при любом x положителен.
Примеры:
- Решить неравенство. x2 + x — 6 > 0.
Решение.
Разложим квадратный трехчлен на множители (x + 3) (x — 2) > 0
Ответ: x (-∞; -3) (2; +∞).
2) (x — 6)2 > 0
Решение:
Это неравенство верно при любом х, кроме х = 6.
Ответ: (-∞; 6) (6; +∞).
3) x² + 4x + 15 < 0.
Решение:
Здесь D < 0, a = 1 > 0. Квадратный трехчлен положителен при всех х.
Ответ: x Î Ø.
Решить неравенства:
- 1 + х — 2х² < 0. Ответ:
- 3х² — 12х + 12 ≤ 0. Ответ:
- 3х² — 7х + 5 ≤ 0. Ответ:
- 2х² — 12х + 18 > 0. Ответ:
- При каких значениях a неравенство
x² — ax > выполняется для любых х? Ответ:
- II. Рациональные неравенства высших степеней, то есть неравенства вида
anxn + an-1xn-1 + … + a1x + a0 > 0 (<0), n>2.
Многочлен высшей степени следует разложить на множители, то есть неравенство записать в виде
an (x — x1) (x — x2) ·…· (x — xn) > 0 (<0).
Отметить на числовой оси точки, в которых многочлен обращается в нуль.
Определить знаки многочлена на каждом промежутке.
Примеры:
1) Решить неравенство x4 — 6x3 + 11x2 — 6x < 0.
Решение:
x4 — 6x3 + 11x2 — 6x = x (x3 — 6x2 + 11x -6) = x (x3 — x2 — 5x2 + 5x +6x — 6) =x (x — 1)( x2 -5x + 6) =
x (x — 1) (x — 2) (x — 3). Итак, x (x — 1) (x — 2) (x — 3)<0
Ответ: (0; 1) (2; 3).
2) Решить неравенство (x -1)5 (x + 2) (x — ½)7 (2x + 1)4 <0.
Решение:
Отметим на числовой оси точки, в которых многочлен обращается в нуль. Это х = 1, х = -2, х = ½, х = — ½.
В точке х = — ½ смены знака не происходит, потому что двучлен (2х + 1) возводится в четную степень, то есть выражение (2x + 1)4 не меняет знак при переходе через точку х = — ½.
Ответ: (-∞; -2) (½; 1).
3) Решить неравенство: х2 (х + 2) (х — 3) ≥ 0.
Решение:
Данное неравенство равносильно следующей совокупности
Решением (1) является х (-∞; -2) (3; +∞). Решением (2) являются х = 0, х = -2, х = 3. Объединяя полученные решения, получаем х Î (-∞; -2] {0} [3; +∞).
Ответ: х (-∞; -2] {0} [3; +∞).
Решить неравенства:
- (5х — 1) (2 — 3х) (х + 3) > 0. Ответ:
- x3 + 5x2 +3x — 9 ≤ 0. Ответ:
- (x — 3) (x — 1)² (3x — 6 — x²) < 0. Ответ:
- (x² -x)² + 3 (x² — x) + 2 ≥ 0. Ответ:
III. Дробно-рациональные неравенства.
При решении таких неравенств можно придерживаться следующей схемы.
- Перенести все члены неравенства в левую часть.
- Все члены неравенства в левой части привести к общему знаменателю, то есть неравенство записать в виде
> 0 (<0).
- Найти значения х, при которых функция y=может менять свой знак. Это корни уравнений
- Нанести найденные точки на числовую ось. Эти точки разбивают множество действительных чисел на промежутки, в каждом их которых функция будет знакопостоянной.
- Определить знак в каждом промежутке, вычисляя, например, значение данного отношения в произвольной точке каждого промежутка.
- Записать ответ, обращая особое внимание на граничные точки промежутков. При решении строгого неравенства >0 (<0) граничные точки в ответ не включаются. При решении нестрогого неравенства ≥ 0 ( ≤ 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.
Примеры.
1). Решить неравенство .
Решение: > 0, > 0, > 0
Найдем нули числителя и знаменателя. Это х = 3, х = 5, х=1. Наносим найденные точки на числовую ось и определяем знаки в каждом промежутке
Выбираем любой х(5; +), например х = 10. Тогда < 0.
Выбираем х = 4 (3; 5).
Получаем > 0. При х = 2 (1; 3). Получаем > 0.
Наконец, при х = 0 (-; 1). Вычисляем < 0.
Ответ: х (1; 3) (3; 5).
2). Найти сумму целых решений неравенства.
Решение. Найдем нули числителя и знаменателя дроби. Это х = -1, х=8, х = 3, х= 5.
Нанесем найденные точки на числовую ось и определим знак дроби в каждом промежутке, вычисляя значение этой дроби в произвольной точке каждого промежутка.
Решением исходного неравенства является
х [-1, 3) (3; 5) {8}. Найдем сумму целых решений: -1 +1+0+ 2 + 4 + 8 = =14.
Ответ: 14.
Что значит найдите сумму целых решений неравенства
Обновлено 5 марта, 2022
Сумма целых решений неравенства
Нужно найти сумму целых решений неравенства 
Не пойму с чего начать. И не пойму как выразить x 🙁
Допустим знак корня распространяется на оба множителя
Замена 7–3x=u
√((u+2)(u–2)) ≥ 0
(u+2)(u–2) ≥ 0
u ≤ –2 ∨ u ≥ 2
7–3x ≤ –2 ∨ 7–3x ≥ 2
–3x ≤ –9 ∨ –3x ≥ –5
x ≥ 3 ∨ x ≤ 5/3
Если добавить условие x ≥ -1, то решение будет составлять множество [-1;5/3]∪[3;+∞), в котором бесконечно много целых решений.
При таком условии вопрос некорректен.
Значит имелось в виду, что знак корня распространяется только на первый множитель
√(u+2) (u-2) ≥ 0
число под корнем должно быть неотрицательным
второй множитель может быть отрицательным, только если первый равен нулю
u+2 ≥ 0 ∧ ((u–2) ≥ 0 ∨ u+2 = 0)
u ≥ –2 ∧ (u ≥ 2 ∨ u = –2)
(u ≥ –2 ∧ u = –2) ∨ (u ≥ –2 ∧ u ≥ 2)
u=–2 ∨ u ≥ 2
7–3x = –2 ∨ 7–3x ≥ 2
–3x=–9 ∨ –3x ≥ –5
x=3 ∨ x ≤ 5/3
с добавлением условия x≥–1 решение будет составлять множество [–1;5/3]∪ <3>
целые решения это числа –1,0,1,3
их сумма равна 2
!поправочка, их сумма равна 3, конечно
Выпишите ОДЗ: x ≤ 3; Затем методом интервалов найдите решения. Должно получиться так:
Сумма целых решений, удовлетворяющих условию: -1 + 0 + 1 + 3 = 3
Источник
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Люди которые понимают в матем.
Скажите, что значит найти
сумму целых решений неравенства.
Приложения:
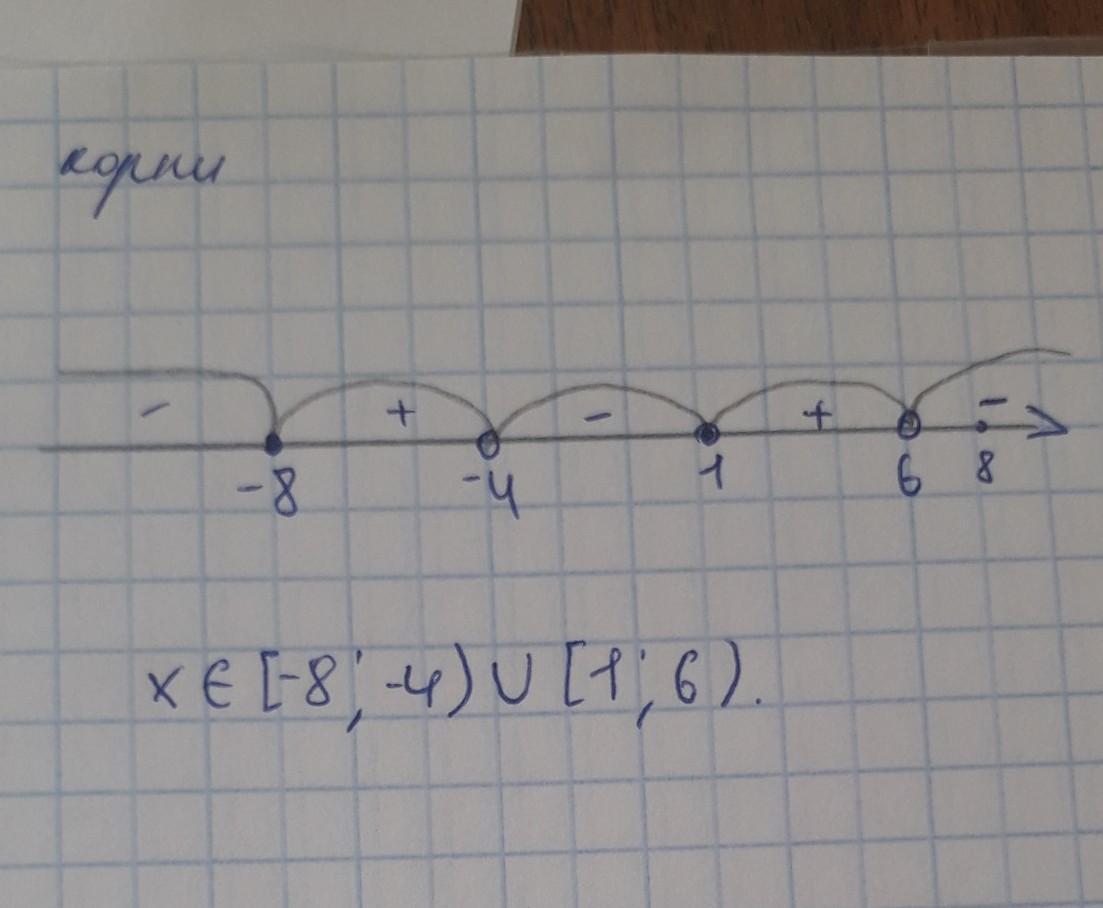
Ответы
Автор ответа: zinaidazina
5
1) Перечислим все целые из первого промежутка [-8; -4)
-8; -7; -6; -5
всего четыре числа.
2) Перечислим все целые из второго промежутка [1; 6)
1; 2; 3; 4; 5
всего 5 чисел.
3) А теперь их сложим — это и будет сумма целых решений неравенства.
-8+(-7) +(-6) + (-5 ) + 1+2+3+4+5 = — 11
dushkaaa:
Спасибо большое, наконец-то поняла)
Интересные вопросы
Предмет: Физика,
автор: kirillkarasev290606


















