Сумма и произведение цифр числа
Одной из часто используемых задач для начинающих изучать программирование является нахождение суммы и произведения цифр числа. Число может вводиться с клавиатуры или генерироваться случайно. Задача формулируется так:
Дано число. Найти сумму и произведение его цифр.
Например, сумма цифр числа 253 равна 10-ти, так как 2 + 5 + 3 = 10. Произведение цифр числа 253 равно 30-ти, так как 2 * 5 * 3 = 30.
В данном случае задача осложняется тем, что количество разрядов числа заранее (на момент написания программы) не известно. Это может быть и трехзначное число, как в примере выше, и восьмизначное, и однозначное.
Обычно предполагается, что данная задача должна быть решена арифметическим способом и с использованием цикла. То есть с заданным число должны последовательно выполняться определенные арифметические действия, позволяющие извлечь из него все цифры, затем сложить их и перемножить.
При этом используются операции деления нацело и нахождения остатка. Если число разделить нацело на 10, произойдет «потеря» последней цифры числа. Например, 253 ÷ 10 = 25 (остаток 3). С другой стороны, эта потерянная цифра есть остаток от деления. Получив эту цифру, мы можем добавить ее к сумме цифр и умножить на нее произведение цифр числа.
Пусть n – само число, suma – сумма его цифр, а mult – произведение. Тогда алгоритм нахождения суммы и произведения цифр можно словесно описать так:
- Переменной suma присвоить ноль.
- Переменной mult присвоить единицу. Присваивать 0 нельзя, так как при умножении на ноль результат будет нулевым.
- Пока значение переменной n больше нуля повторять следующие действия:
- Найти остаток от деления значения n на 10, то есть извлечь последнюю цифру числа.
- Добавить извлеченную цифру к сумме и увеличить на эту цифру произведение.
- Избавиться от последнего разряда числа n путем деления нацело на 10.
В языке Python операция нахождения остатка от деления обозначается знаком процента — %. Деление нацело — двумя слэшами — //.
Код программы на языке Python
n = int(input()) suma = 0 mult = 1 while n > 0: digit = n % 10 suma = suma + digit mult = mult * digit n = n // 10 print("Сумма:", suma) print("Произведение:", mult)
Пример выполнения:
253 Сумма: 10 Произведение: 30
Изменение значений переменных можно записать в сокращенном виде:
... while n > 0: digit = n % 10 suma += digit mult *= digit n //= 10 ...
Приведенная выше программа подходит только для нахождения суммы и произведения цифр натуральных чисел, то есть целых чисел больше нуля. Если исходное число может быть любым целым, следует учесть обработку отрицательных чисел и нуля.
Если число отрицательное, это не влияет на сумму его цифр. В таком случае достаточно будет использовать встроенную в Python функции abc, которая возвращает абсолютное значение переданного ей аргумента. Она превратит отрицательное число в положительное, и цикл while с его условием n > 0 будет работать как и прежде.
Если число равно нулю, то по логике вещей сумма его цифр и их произведение должны иметь нулевые значения. Цикл срабатывать не будет. Поскольку исходное значение mult — это 1, следует добавить проверку на случай, если заданное число — это ноль.
Программа, обрабатывающая все целые числа, может начинаться так:
n = abs(int(input())) suma = 0 mult = 1 if n == 0: mult = 0 ...
Заметим, если в самом числе встречается цифра 0 (например, 503), то произведение всех цифр будет равно нулю. Усложним задачу:
Вводится натуральное число. Найти сумму и произведение цифр, из которых состоит это число. При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
Для решения такой задачи в цикл добавляется проверка извлеченной цифры на ее неравенство нулю. Делать это надо до умножения на нее значения переменной-произведения.
n = int(input()) suma = 0 mult = 1 while n > 0: digit = n % 10 if digit != 0: suma += digit mult *= digit n = n // 10 print("Сумма:", suma) print("Произведение:", mult)
Обратим внимание, что заголовок условного оператора if digit != 0: в Python можно сократить до просто if digit:. Потому что 0 — это False. Все остальные числа считаются истиной.
Приведенный выше математический алгоритм нахождения суммы и произведения цифр числа можно назвать классическим, или универсальным. Подобным способом задачу можно решить на всех императивных языках, независимо от богатства их инструментария. Однако средства языка программирования могут позволить решить задачу другим, зачастую более простым, путем. Например, в Python можно не преобразовывать введенную строку к числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу int:
a = input() suma = 0 mult = 1 for digit in a: suma += int(digit) mult *= int(digit) print("Сумма:", suma) print("Произведение:", mult)
Если добавить в код проверку, что извлеченный символ строки действительно является цифрой, то программа станет более универсальной. С ее помощью можно будет считать не только сумму и произведение цифр целых чисел, но и вещественных, а также цифр, извлекаемых из произвольной строки.
n = input() suma = 0 mult = 1 for digit in n: if digit.isdigit(): suma += int(digit) mult *= int(digit) print("Сумма:", suma) print("Произведение:", mult)
Пример выполнения:
это3 чи3с9ло! Сумма: 15 Произведение: 81
Строковый метод isdigit проверяет, состоит ли строка только из цифр. В нашем случае роль строки играет одиночный, извлеченный на текущей итерации цикла, символ.
Глубокое знание языка Python позволяет решить задачу более экзотическими способами:
import functools n = input() n = [int(digit) for digit in n] suma = sum(n) mult = functools.reduce(lambda x, y: x*y, n) print("Сумма:", suma) print("Произведение:", mult)
Выражение [int(digit) for digit in n] представляет собой генератор списка. Если была введена строка "234", будет получен список чисел: [2, 3, 4].
Встроенная функция sum считает сумму элементов переданного ей аргумента.
Функция reduce модуля functools принимает два аргумента — лямбда-выражение и в данном случае список. Здесь в переменной x происходит накопление произведения, а y принимает каждое следующее значение списка.
Больше задач в PDF
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a number, we need to find sum of its digits using recursion.
Examples:
Input : 12345
Output : 15
Input : 45632
Output :20
The step-by-step process for a better understanding of how the algorithm works.
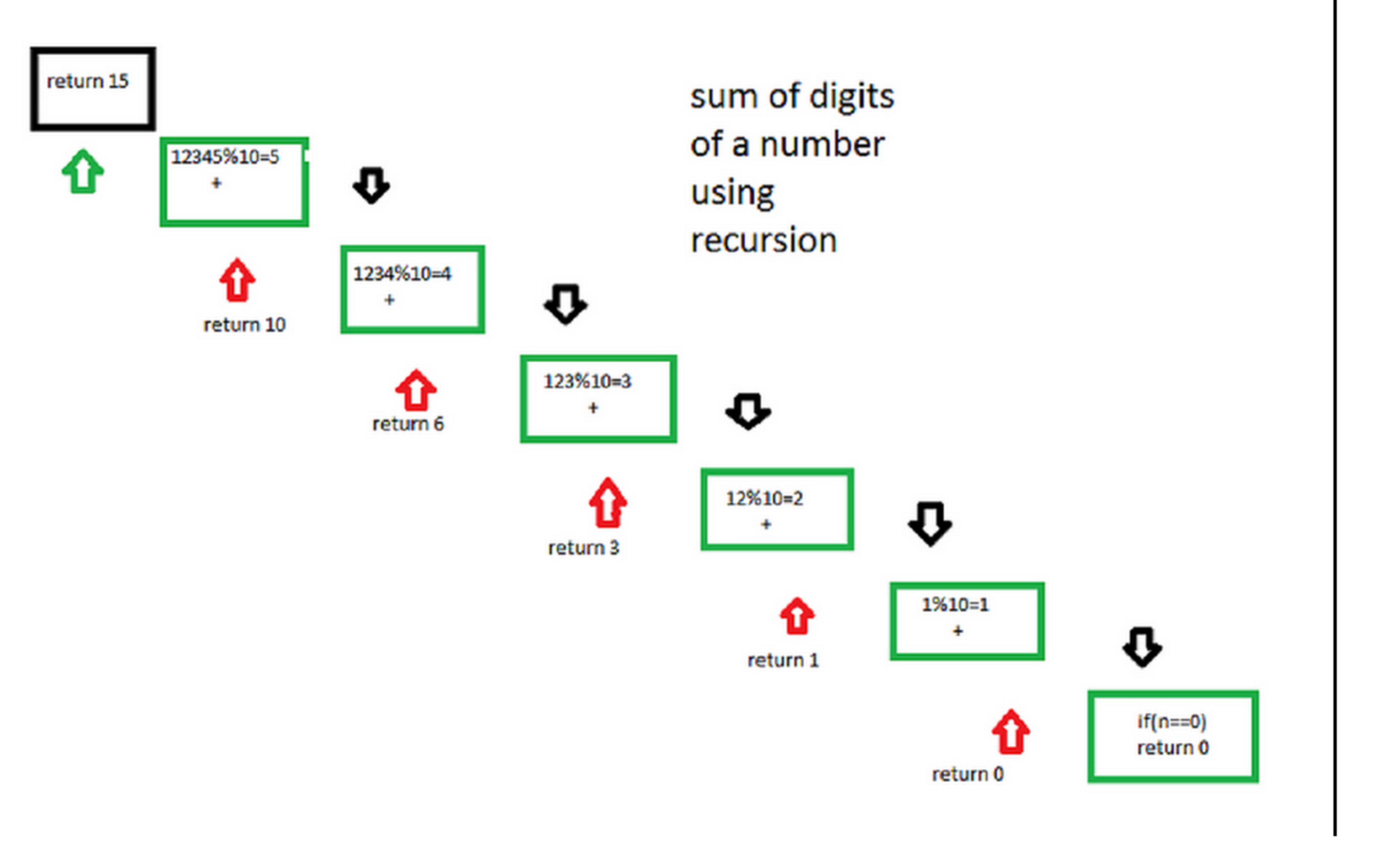
Let the number be 12345.
Step 1-> 12345 % 10 which is equal-too 5 + ( send 12345/10 to next step )
Step 2-> 1234 % 10 which is equal-too 4 + ( send 1234/10 to next step )
Step 3-> 123 % 10 which is equal-too 3 + ( send 123/10 to next step )
Step 4-> 12 % 10 which is equal-too 2 + ( send 12/10 to next step )
Step 5-> 1 % 10 which is equal-too 1 + ( send 1/10 to next step )
Step 6-> 0 algorithm stops
following diagram will illustrate the process of recursion
C++
#include <bits/stdc++.h>
using namespace std;
int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
int main()
{
int num = 12345;
int result = sum_of_digit(num);
cout << "Sum of digits in "<< num
<<" is "<<result << endl;
return 0;
}
C
#include <stdio.h>
int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
int main()
{
int num = 12345;
int result = sum_of_digit(num);
printf("Sum of digits in %d is %dn", num, result);
return 0;
}
Java
import java.io.*;
class sum_of_digits
{
static int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
public static void main(String args[])
{
int num = 12345;
int result = sum_of_digit(num);
System.out.println("Sum of digits in " +
num + " is " + result);
}
}
Python3
def sum_of_digit( n ):
if n == 0:
return 0
return (n % 10 + sum_of_digit(int(n / 10)))
num = 12345
result = sum_of_digit(num)
print("Sum of digits in",num,"is", result)
C#
using System;
class GFG {
static int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
public static void Main()
{
int num = 12345;
int result = sum_of_digit(num);
Console.WriteLine("Sum of digits in " +
num + " is " + result);
}
}
PHP
<?php
function sum_of_digit($n)
{
if ($n == 0)
return 0;
return ($n % 10 +
sum_of_digit($n / 10));
}
$num = 12345;
$result = sum_of_digit($num);
echo("Sum of digits in " . $num . " is " . $result);
?>
Javascript
<script>
function sum_of_digit(n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(parseInt(n / 10)));
}
var num = 12345;
var result = sum_of_digit(num);
document.write( "Sum of digits in "+ num
+" is "+result );
</script>
Output:
Sum of digits in 12345 is 15
Besides writing (n==0 , then return 0) in the code given above we can also write it in this manner , there will be no change in the output .
if(n<10) return n; By writing this there will be no need to call the function for the numbers which are less than 10
Time complexity : O(logn) where n is the given number.
Auxiliary space : O(logn) due to recursive stack space.
Last Updated :
16 Jun, 2022
Like Article
Save Article
На чтение 4 мин Просмотров 13к. Опубликовано
Нахождение суммы цифр в числе — одна из базовых операций, которую может потребоваться выполнить в процессе программирования. Она может быть использована в различных задачах, например, при работе с кредитными картами, номерами телефонов и другими идентификаторами. Кроме того, вычисление суммы цифр может быть полезно для анализа данных, обработки информации и решения различных математических задач. В Python существует несколько способов нахождения суммы цифр в числе, которые мы рассмотрим в этой статье.
Содержание
- Способы нахождения суммы цифр в числе
- Способ 1: Использование цикла и операции взятия остатка от деления
- Способ 2: Преобразование числа в строку и использование цикла
- Способ 3: Использование рекурсии
Способы нахождения суммы цифр в числе
Существует несколько способов нахождения суммы цифр в числе с использованием языка Python. Один из самых простых способов — это использование цикла и арифметических операций. Второй способ — это преобразование числа в строку и последующее суммирование цифр с помощью цикла. Также можно использовать рекурсию для нахождения суммы цифр в числе. В этой статье мы рассмотрим все эти методы подробнее и покажем, как их использовать в Python.
Способ 1: Использование цикла и операции взятия остатка от деления
Один из наиболее простых способов найти сумму цифр в числе заключается в использовании цикла и операции взятия остатка от деления. Идея заключается в том, чтобы последовательно извлекать цифры из числа путем нахождения остатка от деления на 10 и добавлять их в сумму. Затем нужно целочисленно разделить число на 10 и продолжить процесс до тех пор, пока число не станет равным 0. Когда число станет равным 0, сумма цифр в числе будет содержаться в переменной суммы, которую мы и будем возвращать.
Приведём пример:
number = 12345
sum = 0
while number > 0:
digit = number % 10
sum += digit
number //= 10
print("Сумма цифр числа:", sum)В этом примере мы начинаем с числа number и инициализируем переменную sum нулевым значением. Затем мы запускаем цикл, который будет выполняться, пока number больше нуля.
На каждой итерации цикла мы используем операцию взятия остатка от деления на 10, чтобы получить последнюю цифру числа. Мы добавляем эту цифру к переменной sum, чтобы накапливать сумму цифр, и затем целочисленно делим number на 10, чтобы удалить последнюю цифру числа.
Когда цикл завершается, мы выводим значение переменной sum, которое представляет собой сумму цифр числа.
Способ 2: Преобразование числа в строку и использование цикла
Другой способ нахождения суммы цифр в числе состоит в преобразовании числа в строку и последующем проходе по каждому символу в строке с целью получения числа и добавления его в общую сумму. Данный подход может показаться более интуитивным, так как позволяет оперировать с каждой цифрой непосредственно как с символом. Однако, для больших чисел, этот подход может занять больше времени и занимать больше памяти, чем использование операции взятия остатка от деления.
Приведём пример:
num = 12345
sum_digits = 0
for digit in str(num):
sum_digits += int(digit)
print("Сумма цифр числа", num, "равна", sum_digits)В этом примере мы сначала определяем исходное число num. Затем мы инициализируем переменную sum_digits нулем, которая будет использоваться для хранения суммы цифр в числе. Мы затем используем цикл for для перебора каждой цифры в числе num, которое мы преобразуем в строку с помощью функции str(). Внутри цикла мы преобразуем каждую цифру обратно в целое число с помощью функции int() и добавляем его к сумме цифр sum_digits.
Наконец, мы выводим сообщение, которое отображает исходное число num и его сумму цифр.
Способ 3: Использование рекурсии
Еще одним способом нахождения суммы цифр числа в Python является использование рекурсии. Рекурсивная функция — это функция, которая вызывает саму себя. Для решения этой задачи мы можем написать рекурсивную функцию, которая будет находить сумму цифр числа, путем разделения числа на цифры и вызова функции для каждой цифры. На каждом уровне рекурсии мы будем добавлять текущую цифру к сумме, а затем вызывать функцию с оставшейся частью числа.
Преимущество рекурсивного подхода заключается в том, что он более компактен и элегантен, чем циклический подход, и может использоваться для решения широкого спектра задач.
Приведём пример:
def sum_of_digits(n):
if n < 10:
return n
else:
return n % 10 + sum_of_digits(n // 10)Эта функция принимает целое число n и рекурсивно находит сумму его цифр. Если число n меньше 10, то оно возвращается, так как оно само по себе является суммой своих цифр. В противном случае, функция находит последнюю цифру числа n с помощью операции взятия остатка от деления на 10 (n % 10), а затем вызывает себя же для нахождения суммы оставшихся цифр числа (sum_of_digits(n // 10)). Результатом работы функции является сумма всех цифр числа n.
Например, вызов sum_of_digits(123) вернет 6, так как сумма цифр числа 123 равна 1 + 2 + 3 = 6.
Перейти к содержанию
Сумма и произведение цифр числа
Просмотров 8.4к. Обновлено 29 октября 2021
Если трехзначное число нацело разделить на 100, то получим число сотен, т.е. первую цифру этого числа.
Если найти остаток от деления на 10 любого целого числа, то этот остаток покажет число единиц в этом числе. Таким образом извлекается последняя цифра числа.
Чтобы извлечь среднюю цифру трехзначного числа (показывающую количество десятков), можно выполнить два действия:
- Разделить число нацело на 10. Тем самым избавиться от последней цифры трехзначного числа, превратив его в двузначное.
- Найти остаток от деления полученного двузначного числа на 10. Этот остаток и будет средняя цифра первоначального трехзначного числа.
Извлекая вышеописанным способом цифры числа их надо присвоить переменным. Т.к. цифр три, то и переменных будет три. После этого выполнить сложение и умножение значений переменных.
Pascal
произведение цифр числа паскаль и сумма цифр числа паскаль
var
n: integer;
a,b,c: byte;
begin
readln(n);
a := n div 100;
b := n div 10 mod 10;
c := n mod 10;
writeln('Сумма: ',a+b+c);
writeln('Произведение: ',a*b*c);
end.
Язык Си
произведение цифр числа си и сумма цифр числа си
#includemain() {
int n,a,b,c;
scanf("%d", &n);
a = n / 100;
b = n / 10 % 10;
c = n % 10;
printf("Сумма: %dn", a+b+c);
printf("Произведение: %dn", a*b*c);
}
349
Сумма: 16
Произведение: 108
Целочисленное деление выполняется в том случае, если оба операнда целые. Т.е. у целочисленного деления нет специального знака, а выбор между ним и обычным делением зависит от операндов. Если хотя бы один из операндов вещественное число, то и деление будет обычным.
Python
произведение цифр числа Python и сумма цифр числа Python
n = input("Введите трехзначное число: ")
n = int(n)d1 = n % 10
d2 = n % 100 // 10
d3 = n // 100print("Сумма цифр числа:", d1 + d2 + d3)
print("Произведение цифр числа:", d1 * d2 * d3)
Введите трехзначное число: 742
Сумма цифр числа: 13
Произведение цифр числа: 56
КуМир
алг сумма цифр
нач
ввод n
a := div(n,100)
b := mod(div(n,10),10)
c := mod(n,10)
вывод "Сумма: ", a+b+c, нс
вывод "Произведение: ", a*b*c, нс
кон
Basic-256
input na = n 100
b = n 10 % 10
c = n % 10print a+b+c
print a*b*c
Обратите внимание на знак целочисленного деления. Это обратный слэш (), в то время как обычное деление обозначается обычным слэшем (/).
В этой статье мы разберем, как определяется сумма цифр числа при помощи кода на Python. Давайте сразу на простом примере поясним, что имеется в виду. Для вычисления такой суммы мы просто складываем цифры, которыми записано число, и при этом игнорируем их разряды. Допустим, у нас есть число 567. Мы можем вычислить сумму его цифр как 5 + 6 + 7 и получить ответ 18.
Наша цель состоит в том, чтобы определить сумму цифр числа, переданного в качестве входных данных в коде на Python.
Пример:
n = 54 Результат: 9 n = 121 Результат: 4
Сначала мы разбиваем число на отдельные цифры, а затем в качестве результата получаем сумму этих цифр. Чтобы разбить число на цифры, мы можем использовать оператор деления по модулю %, а затем, чтобы сократить число на разряд, можем использовать оператор целочисленного деления //.
Различные способы нахождения суммы цифр числа
Использование встроенных функций str() и int()
Чтобы преобразовать число в строку, используется функция str(). Для преобразования цифровых символов в целое число используется функция int().
Мы преобразуем число в строку и при помощи цикла перебираем все цифровые символы этой строки. В каждой итерации число, обозначаемое текущей цифрой, прибавляется к общей сумме.
Порядок алгоритма:
- Принимаем введенное пользователем значение числа
- Создаем переменную, в которой будем хранить результат
- Преобразуем число в строку
- Создаем цикл для итерации по полученной строке
- Внутри цикла преобразуем каждое строковое значение числа в целочисленный тип и добавляем в переменную, в которой хранится результат.
Код примера:
# Функция для получения суммы цифр числа
def getSum(n):
sum = 0
for digit in str(n):
sum += int(digit)
return sum
n = 569
print(getSum(n))
# Результат
# 20
Использование итерации
Здесь сумма цифр числа вычисляется при помощи цикла. Циклы используются для непрерывного выполнения определенного фрагмента кода. В языке Python циклы создаются при помощи операторов for и while.
Чтобы получить крайнюю правую цифру нашего числа, мы можем использовать тот факт, что она равна остатку от деления на 10. В Python для получения остатка от деления используется оператор %. Далее, чтобы перейти к следующей цифре, мы производим целочисленное деление на 10.
Порядок алгоритма:
- Создаем функцию для нахождения суммы цифр числа
n - Объявляем переменную
sumдля хранения суммы цифр - Создаем цикл
while, который будет работать, пока значениеnбудет больше 0 - Остаток от деления числа на 10 прибавляем к переменной
sum - Меняем
nнаn // 10(результат целочисленного деления на 10) - Получаем число от пользователя
- Вызываем созданную ранее функцию и передаем ей в качестве аргумента полученное на предыдущем шаге число
- Выводим в консоль результат работы данной функции.
Пример кода:
# Функция для получения суммы цифр числа
def getSum(n):
sum = 0
while (n != 0):
sum = sum + (n % 10)
n = n//10
return sum
n = 569
print(getSum(n))
# Результат
# 20
Использование рекурсии
Рекурсия – это процесс решения задачи при помощи определения более простой версии этой самой задачи. Соответствующая функция называется рекурсивной. Использование рекурсии позволяет обойтись без применения циклов.
Алгоритм поиска суммы цифр числа при помощи рекурсии:
- Создаем функцию для нахождения суммы цифр числа
n - Если число
nменьше 10, то в качестве значения возвращаетсяn - В противном случае находим остаток от деления на 10 и производим целочисленное деление на 10
- Рекурсивно вызываем нашу функцию, передавая ей в качестве аргумента
n // 10 - Добавляем остаток от деления на 10 к значению, которое возвращает функция
- Получаем число от пользователя
- Вызываем созданную ранее функцию и передаем ей в качестве аргумента полученное на предыдущем шаге число
- Выводим в консоль результат работы данной функции.
Пример кода:
# Функция для получения суммы цифр числа
def sumDigits(no):
return 0 if no == 0 else int(no % 10) + sumDigits(int(no / 10))
# Работа кода
n = 569
print(sumDigits(n))
# Результат
# 20
Использование метода sum()
Метод sum() используется для нахождения суммы всех чисел в переданном списке.
Сначала мы преобразуем число в строку при помощи метода str(). Затем мы разбиваем строку и преобразуем ее в список чисел при помощи методов split() и map() соответственно. А потом вычисляем сумму всех чисел данного списка при помощи метода sum().
Порядок алгоритма:
- Создаем функцию для нахождения суммы цифр числа
n - Преобразуем число в строку при помощи метода
str() - Затем разбиваем строку и преобразуем ее в список чисел при помощи методов
split()иmap()соответственно - Для вычисления суммы чисел, входящих в список, вызывается метод
sum().
Пример кода:
# Функция для получения суммы цифр числа
def getSum(n):
strr = str(n)
list_of_number = list(map(int, strr.strip()))
return sum(list_of_number)
n = 569
print(getSum(n))
# Результат
# 20
Заключение
Сумма цифр числа — это сумма всех чисел, обозначаемых цифрами, которыми записано это число. Например, сумма цифр десятичного числа 9045 будет равна сумме чисел 9, 0, 4 и 5. То есть 9 + 0 + 4 + 5 = 18.
Найти сумму цифр числа можно разными способами. Мы разобрали использование встроенных функций, применение рекурсии и циклов.
Перевод статьи “Sum of Digits of a Number in Python”.