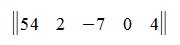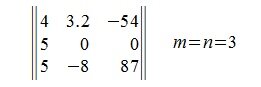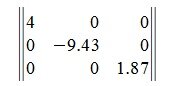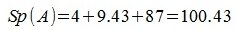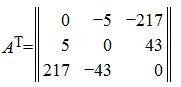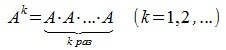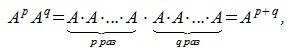|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
1 |
|
Найти суммы элементов диагонали в матрице23.06.2017, 21:17. Показов 13347. Ответов 15
Помогите пожалуйста, в MathCAD с помощью какой формулы можно найти сумму элементов диагоналей?
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
23.06.2017, 21:43 |
2 |
|
Вот так можно Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
23.06.2017, 21:50 [ТС] |
3 |
|
Спасибо за быстрый ответ!
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
23.06.2017, 22:05 |
4 |
|
Эти формулы без всяких изменений работают для всех шести диагоналей при переходе к матрице любого размера n=9. А в одну формулу все шесть сумм воткнуть невозможно, но можно оформить в виде одной функции Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
23.06.2017, 22:14 [ТС] |
5 |
|
Большое спасибо!!! Если Вам не сложно, можете мне подсказать как можно оформить в виде одной функции суммы элементов основных диагоналей? Вот эти три суммы внести в функцию…
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
28.06.2017, 10:06 |
6 |
|
РешениеВот так можно Миниатюры
0 |
Сообщение было отмечено VSI как решение
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
28.06.2017, 19:56 [ТС] |
7 |
|
Вы не могли бы взглянуть, что у меня получилось… Миниатюры
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
29.06.2017, 07:12 |
8 |
|
РешениеЕсли требуется найти суммы всех диагоналей (включая отдельные угловые клетки), то задача даже упрощается Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
29.06.2017, 08:57 [ТС] |
9 |
|
Мне нужно найти суммы элементов диагоналей.
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
29.06.2017, 09:15 |
10 |
|
Вы, что не видите, что это у меня сделано в виде функции, которая работает абсолютно для любой матрицы и выводит эти суммы в два столбца (две строки), что касается угловых клеток (соответствующих первому и последнему элементам выводимых строк), то их можно просто не использовать.
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
29.06.2017, 09:30 |
11 |
|
Вот скрин для матрицы 9 на 9, где показан порядок нумерации диагоналей (прямых и побочных), начиная от соответствующих углов, который всегда можно изменить по своему вкусу Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
29.06.2017, 09:57 [ТС] |
12 |
|
А что бы исключить угловые клетки, Нужно изменить for K= 1..2n-3?
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
29.06.2017, 10:07 |
13 |
|
Внутри функции, которая сейчас имеет максимально краткий код, придется вносить дополнительно условные операторы. Проще просто вырезать из получившегося массива нужный фрагмент без крайних элементов (мне лично непонятно, почему эти угловые клетки мешают Вам?). Кроме этого усложняется зависимость между индексом k и индексами столбцов и строк i, j — Вы же собираетесь использовать эти суммы в итерационном алгоритме восстановления матрицы.
0 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
29.06.2017, 10:30 [ТС] |
14 |
|
Да верно, я использую эти суммы для итерации матрицы.
0 |
|
0 / 0 / 0 Регистрация: 22.06.2017 Сообщений: 19 |
|
|
29.06.2017, 21:12 [ТС] |
15 |
|
Все же проблема у меня с этой итерацией.. Миниатюры
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
30.06.2017, 14:53 |
16 |
|
У Вас никакой итерации по диагоналям нет. Должна восстанавливаться двухмерная матрица, а у Вас какие-то непонятные действия с одномерным массивом! Вернитесь в соседнюю ветку Реконструкция матрицы итерационным методом
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
30.06.2017, 14:53 |
|
Помогаю со студенческими работами здесь В заданной матрице вычислить отношение суммы элементов побочной диагонали к количеству положительных элементов
В заданной матрице вычислите две суммы элементов, расположенных выше и ниже побочной диагонали Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 16 |
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a 2D square matrix, find the sum of elements in Principal and Secondary diagonals. For example, consider the following 4 X 4 input matrix.
A00 A01 A02 A03 A10 A11 A12 A13 A20 A21 A22 A23 A30 A31 A32 A33
The primary diagonal is formed by the elements A00, A11, A22, A33.
- Condition for Principal Diagonal: The row-column condition is row = column.
The secondary diagonal is formed by the elements A03, A12, A21, A30. - Condition for Secondary Diagonal: The row-column condition is row = numberOfRows – column -1.
Examples :
Input : 4 1 2 3 4 4 3 2 1 7 8 9 6 6 5 4 3 Output : Principal Diagonal: 16 Secondary Diagonal: 20 Input : 3 1 1 1 1 1 1 1 1 1 Output : Principal Diagonal: 3 Secondary Diagonal: 3
Method 1: In this method, we use two loops i.e. a loop for columns and a loop for rows and in the inner loop we check for the condition stated above:
Implementation:
C
#include <stdio.h>
const int M = 4;
const int N = 4;
void printDiagonalSums(int mat[M][N])
{
int principal = 0, secondary = 0;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
if (i == j)
principal += mat[i][j];
if ((i + j) == (N - 1))
secondary += mat[i][j];
}
}
printf("%s", "Principal Diagonal:");
printf("%dn", principal);
printf("%s", "Secondary Diagonal:");
printf("%dn", secondary);
}
int main()
{
int a[][4] = {{1, 2, 3, 4},
{5, 6, 7, 8},
{1, 2, 3, 4},
{5, 6, 7, 8}};
printDiagonalSums(a);
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
void printDiagonalSums(int mat[][MAX], int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j)
principal += mat[i][j];
if ((i + j) == (n - 1))
secondary += mat[i][j];
}
}
cout << "Principal Diagonal:" << principal << endl;
cout << "Secondary Diagonal:" << secondary << endl;
}
int main()
{
int a[][MAX] = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 },
{ 1, 2, 3, 4 }, { 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
return 0;
}
Java
import java.io.*;
public class GFG {
static void printDiagonalSums(int [][]mat,
int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j)
principal += mat[i][j];
if ((i + j) == (n - 1))
secondary += mat[i][j];
}
}
System.out.println("Principal Diagonal:"
+ principal);
System.out.println("Secondary Diagonal:"
+ secondary);
}
static public void main (String[] args)
{
int [][]a = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
}
}
Python3
MAX = 100
def printDiagonalSums(mat, n):
principal = 0
secondary = 0;
for i in range(0, n):
for j in range(0, n):
if (i == j):
principal += mat[i][j]
if ((i + j) == (n - 1)):
secondary += mat[i][j]
print("Principal Diagonal:", principal)
print("Secondary Diagonal:", secondary)
a = [[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ]]
printDiagonalSums(a, 4)
C#
using System;
public class GFG {
static void printDiagonalSums(int [,]mat,
int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j)
principal += mat[i,j];
if ((i + j) == (n - 1))
secondary += mat[i,j];
}
}
Console.WriteLine("Principal Diagonal:"
+ principal);
Console.WriteLine("Secondary Diagonal:"
+ secondary);
}
static public void Main ()
{
int [,]a = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
}
}
PHP
<?php
$MAX = 100;
function printDiagonalSums($mat, $n)
{
global $MAX;
$principal = 0;
$secondary = 0;
for ($i = 0; $i < $n; $i++)
{
for ($j = 0; $j < $n; $j++)
{
if ($i == $j)
$principal += $mat[$i][$j];
if (($i + $j) == ($n - 1))
$secondary += $mat[$i][$j];
}
}
echo "Principal Diagonal:" ,
$principal ,"n";
echo "Secondary Diagonal:",
$secondary ,"n";
}
$a = array (array ( 1, 2, 3, 4 ),
array ( 5, 6, 7, 8 ),
array ( 1, 2, 3, 4 ),
array ( 5, 6, 7, 8 ));
printDiagonalSums($a, 4);
?>
Javascript
<script>
const MAX = 100;
void printDiagonalSums(mat, n)
{
let principal = 0, secondary = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
if (i == j)
principal += mat[i][j];
if ((i + j) == (n - 1))
secondary += mat[i][j];
}
}
document.write("Principal Diagonal:" + principal + "<br>");
document.write("Secondary Diagonal:" + secondary + "<br>");
}
let a = [ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ],
[ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ];
printDiagonalSums(a, 4);
</script>
Output
Principal Diagonal:18 Secondary Diagonal:18
Time Complexity: O(N*N), as we are using nested loops to traverse N*N times.
Auxiliary Space: O(1), as we are not using any extra space.
Method 2( Efficient Approach): In this method, we use one loop i.e. a loop for calculating the sum of both the principal and secondary diagonals:
Implementation:
C
#include <stdio.h>
#include <stdlib.h>
const int M = 4;
const int N = 4;
void printDiagonalSums(int mat[M][N])
{
int principal = 0, secondary = 0;
for (int i = 0; i < N; i++)
{
principal += mat[i][i];
secondary += mat[i][N - i - 1];
}
printf("%s","Principal Diagonal:");
printf("%dn", principal);
printf("%s", "Secondary Diagonal:");
printf("%dn", secondary);
}
int main()
{
int a[4][4] = {{1, 2, 3, 4},
{5, 6, 7, 8},
{1, 2, 3, 4},
{5, 6, 7, 8}};
printDiagonalSums(a);
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
void printDiagonalSums(int mat[][MAX], int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
principal += mat[i][i];
secondary += mat[i][n - i - 1];
}
cout << "Principal Diagonal:" << principal << endl;
cout << "Secondary Diagonal:" << secondary << endl;
}
int main()
{
int a[][MAX] = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 },
{ 1, 2, 3, 4 }, { 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
return 0;
}
Java
import java.io.*;
public class GFG {
static void printDiagonalSums(int [][]mat,
int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
principal += mat[i][i];
secondary += mat[i][n - i - 1];
}
System.out.println("Principal Diagonal:"
+ principal);
System.out.println("Secondary Diagonal:"
+ secondary);
}
static public void main (String[] args)
{
int [][]a = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
}
}
Python3
MAX = 100
def printDiagonalSums(mat, n):
principal = 0
secondary = 0
for i in range(0, n):
principal += mat[i][i]
secondary += mat[i][n - i - 1]
print("Principal Diagonal:", principal)
print("Secondary Diagonal:", secondary)
a = [[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ]]
printDiagonalSums(a, 4)
C#
using System;
public class GFG {
static void printDiagonalSums(int [,]mat,
int n)
{
int principal = 0, secondary = 0;
for (int i = 0; i < n; i++) {
principal += mat[i,i];
secondary += mat[i,n - i - 1];
}
Console.WriteLine("Principal Diagonal:"
+ principal);
Console.WriteLine("Secondary Diagonal:"
+ secondary);
}
static public void Main ()
{
int [,]a = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 } };
printDiagonalSums(a, 4);
}
}
PHP
<?php
$MAX = 100;
function printDiagonalSums($mat, $n)
{
global $MAX;
$principal = 0; $secondary = 0;
for ($i = 0; $i < $n; $i++)
{
$principal += $mat[$i][$i];
$secondary += $mat[$i][$n - $i - 1];
}
echo "Principal Diagonal:" ,
$principal ,"n";
echo "Secondary Diagonal:" ,
$secondary ,"n";
}
$a = array(array(1, 2, 3, 4),
array(5, 6, 7, 8),
array(1, 2, 3, 4),
array(5, 6, 7, 8));
printDiagonalSums($a, 4);
?>
Javascript
<script>
function printDiagonalSums(mat,n)
{
let principal = 0, secondary = 0;
for (let i = 0; i < n; i++) {
principal += mat[i][i];
secondary += mat[i][n - i - 1];
}
document.write("Principal Diagonal:"
+ principal+"<br>");
document.write("Secondary Diagonal:"
+ secondary);
}
let a = [[ 1, 2, 3, 4 ],
[5, 6, 7, 8 ],
[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ]];
printDiagonalSums(a, 4);
</script>
Output
Principal Diagonal:18 Secondary Diagonal:18
Time Complexity: O(N), as we are using a loop to traverse N times.
Auxiliary Space: O(1), as we are not using any extra space.
This article is contributed by Mohak Agrawal. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Last Updated :
27 Sep, 2022
Like Article
Save Article
Сумма — диагональный элемент — матрица
Cтраница 1
Сумма диагональных элементов матрицы называется следом матрицы. Индексы S или / ( Trs, Tr) означают, что берется след по состояниям спина S или /, соответственно.
[1]
Суммы диагональных элементов матриц АВ и ВА равны.
[2]
Сумма диагональных элементов матрицы представления называется характером и обозначается х — Из табл. 3 видно, что характер каждого элемента, принадлежащего к одному и тому же классу, один и тот же.
[3]
Суммы диагональных элементов матриц АВ и ВА равны.
[4]
Сумма диагональных элементов матрицы тензора второго ранга называется его линейным инвариантом.
[5]
Хотя характеры — суммы диагональных элементов матриц; представления — не содержат всей информации, имеющейся в матрицах, они все же содержат достаточно информации, чтобы играть важную роль в химии. Одна из причин состоит в том, что-таблицы характеров позволяют с первого взгляда сказать, будет ли интеграл равен нулю без детального его вычисления. Это экономит много времени и позволяет быстро качественно оценить свойства молекул.
[6]
Поскольку характеры представлений равны сумме диагональных элементов матрицы преобразования, то при вычислении характеров всех возможных движений ядер надо учитывать только те ядра, положения равновесия которых остаются на месте при данном преобразовании. Ядрам, которые меняются местами при данном преобразовании, соответствуют недиагональные элементы матрицы преобразования, не дающие вклада в характер представления.
[7]
Поскольку характеры представлений равны сумме диагональных элементов матрицы преобразования, то при вычислении характеров всех возможных движений ядер надо учитывать только те ядра, положения равновесия которых остаются на месте при данном преобразовании.
[8]
В некоторых приложениях важную роль играет сумма диагональных элементов матрицы, именуемая часто шпуром ( нем.
[9]
Докажите, что tr А равен сумме диагональных элементов матрицы оператора А в любом базисе.
[10]
След линейного преобразования линейного пространства над полем С равен сумме диагональных элементов матрицы этого линейного преобразования в любой базе.
[11]
Отмеченная выше связь между суммой корней векового уравнения и суммой диагональных элементов матрицы полного взаимодействия, а также произведением корней и определителем указанной матрицы имеет место для уравнений любого порядка и позволяет вывести полезные соотношения между частотами изотопоза-мещенных молекул.
[12]
Заметим одно важное свойство унитарного преобразования: унитарное преобразование оставляет неизменным сумму диагональных элементов матрицы.
[13]
В (2.54) if А обозначает след матрицы А, который равен сумме диагональных элементов матрицы А.
[14]
Докажите матричное тождество a Matr А аа, где след 1тА есть сумма диагональных элементов матрицы А.
[15]
Страницы:
1
2
3
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
(i=1,2,…m; j=1,2,…n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
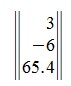
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a11, a22 ,…, ann образуют главную диагональ матрицы. Например:
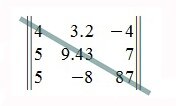
В случае m×n -матриц элементы aii ( i=1,2,…,min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a1n, a2n-1 ,…, an1 образуют побочную диагональ матрицы. Например:
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n, где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
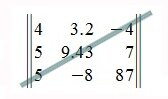
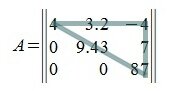
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
|
|
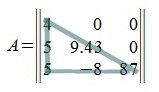
Верхняя треугольная матрица
Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. aij=0, при всех i>j . Например:
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i<j. Например:
Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(AT).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
AT=−A.
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
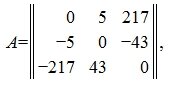
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
C=A+(-1)B.
Для обозначения разности двух матриц используется запись:
C=A-B.
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
A0=E,
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=AT называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
aij=aji ; i=1,2,…n, j=1,2,…n
Как найти сумму элементов матрицы
Матрица или массив элементов представляет собой таблицу определенных значений с фиксированным размером в m строк и n столбцов. Множество выполняемых над матрицей и ее элементами операций позволяет решать различные математические задачи. В частности, одной из таких задач является поиск суммы элементов матрицы. Причем рассматриваемые значения могут быть расположенны как по диагонали, так и в других частях заданного математического объекта.
Запишите матрицу размерностью mхn, где m – число строк, а n – число столбцов объекта. В наиболее простом случае поиска суммы всех элементов матрицы выполните последовательное сложение ее значений. В первой строке первый элемент сложите со вторым, к получившемуся результату прибавьте третий и т.д. до последнего значения строки. Далее к сумме элементов первой строки таким же образом прибавляйте значения второй и всех последующих строк матрицы. Причем при сложении чисел учитывайте их знак. Так, значения -4 и 5 дадут в сумме 1, а -5 + -6 = -11.
Определите сумму элементов на главной диагонали заданной матрицы. Главная диагональ матрицы проходит от ее верхнего левого угла до нижнего правого. Все элементы, стоящие на этой «прямой» сложите между собой. Определив сумму всех чисел на главной диагонали, запишите окончательный результат.
Аналогичным образом вычислите сумму элементов на побочной диагонали рассматриваемой матрицы. Побочной диагональю называется «прямая» проходящая от верхнего левого угла матрицы в нижний правый. Все значения объекта, лежащие на данной диагонали, сложите между собой и запишите результат.
Найдите сумму элементов, стоящих ниже главной диагонали. Для этого проведите по главной диагонали матрицы прямую, отсекающую значения самой диагонали и верхней части объекта. Найдите сумму элементов, расположенных ниже прямой. Для этого желательно складывать значения построчно. Из первой строки ниже главной диагонали возьмите единственный стоящий там элемент, сложите его с первым элементом следующей строки, затем к полученной сумме прибавьте значение второго элемента. Далее перейдите к элементам на третьей строке и т.д., пока не будет произведено сложение последнего, не зачеркнутого элемента матрицы ниже главной диагонали.
Для вычисления суммы элементов матрицы, стоящих выше главной диагонали, выполните аналогичные действия, только в качестве слагаемых рассматривайте элементы стоящие выше зачеркнутой диагонали.