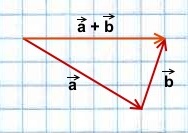
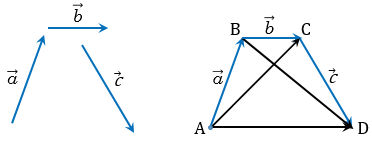
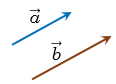Как найти сумму двух векторов правило параллелограмма - Исправление недочетов и поиск решений вместе с Examum.ru

Сложение векторов по правилу параллелограмма

Даны векторы

a→

b→

. Если векторы

a→

b→

исходят из одной точки, то вектор суммы

c→

исходит из общей начальной точки векторов и является диагональю параллелограмма, сторонами которого являются векторы

a→

b→

Запись:

a→+b→=c→

или

AB→+AD→=AC→

Такой приём сложения векторов называется правилом параллелограмма.

Так как

DC→=AB→=b→

, то

a→+b→=AD→+DC→=AC→=c→

; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор

c→

. Поэтому оба способа сложения равноценны.

1. Для любых двух векторов

a→

b→

в силе равенство

a→+b→=b→+a→

(коммутативный, или переместительный, закон сложения).

2. Для любых трёх векторов

a→

b→

c→

в силе равенство

a→+b→+c→=a→+b→+c→

(ассоциативный, или сочетательный, закон сложения).

Источник

Определение

Сумма векторов

— это вектор

с координатами c₁=a₁+b₁, c₂=a₂+b₂, то есть

или

$[(overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 ;b_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Свойства сложения векторов:

Для любых векторов

верны свойства:

1) переместительное:

2) сочетательное:

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Доказательство:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

$[1)overrightarrow a (a_1 ;a_2 ) + overrightarrow b (b_1 ;b_2 ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ),]$

$[overrightarrow b (b_1 ;b_2 ) + overrightarrow a (a_1 ;a_2 ) = (overrightarrow {b_1 + a_1 ;b_2 + a_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Так как соответствующие координаты равны, то эти векторы равны.

Аналогично

$[2)overrightarrow a (a_1 ;a_2 ) + (overrightarrow b (overrightarrow {b_1 ;b_2 } ) + overrightarrow c (c_1 ;c_2 )) = ]$

$[= (overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 + c_1 ;b_2 + c_2 } ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } ),]$

$[(overrightarrow a (a_1 ;a_2 ) + overrightarrow b (overrightarrow {b_1 ;b_2 } )) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } );]$

$[3)overrightarrow a (a_1 ;a_2 ) + overrightarrow 0 (0;0) = (overrightarrow {a_1 + 0;a_2 + 0} ) = (overrightarrow {a_1 ;a_2 } ) = overrightarrow a .]$

Теорема

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Доказательство:

Для точек A (x₁;y₁), B (x₂;y₂), C (x₃;y₃)

$[overrightarrow {AB} (x_2 - x_1 ;y_2 - y_1 ),]$

$[overrightarrow {BC} (x_3 - x_2 ;y_3 - y_2 ),]$

$[overrightarrow {AC} (x_3 - x_1 ;y_3 - y_1 ).]$

Тогда

$[overrightarrow {AB} + overrightarrow {BC} = (overrightarrow {x_2 - x_1 + x_3 - x_2 ;y_2 - y_1 + y_3 - y_2 } ) = ]$

$[= (overrightarrow {x_3 - x_1 ;y_3 - y_1 } ) = overrightarrow {AC} .]$

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

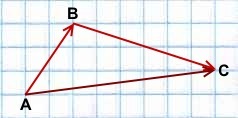
(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

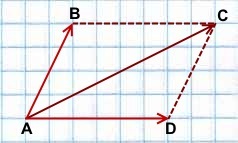
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Пример.

Построить сумму векторов

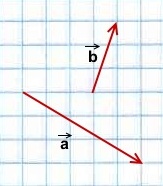
Решение:

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

вектор

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

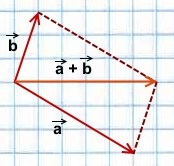
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

Сложение коллинеарных векторов

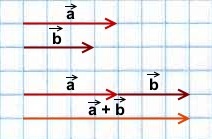
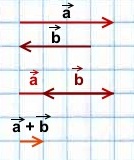
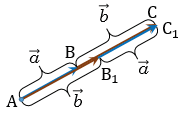
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Источник

В статье Понятие вектора мы сказали, что векторы можно складывать друг с другом. Рассмотрим этот вопрос подробнее.

Пусть нам даны два вектора a⃗vec{a} и b⃗vec{b}. Что понимать под суммой этих двух векторов, то есть под a⃗+b⃗vec{a}+vec{b}? Во первых, сумма двух векторов это вектор. То есть, если мы складываем два вектора (две стрелки) то снова получаем вектор (стрелку). Существуют два способа (или правила) как можно складывать векторы. Они, конечно, дают один и тот же самый результат. Говорят о правиле треугольника и правиле параллелограмма. Оба эти правила графические, то есть сумма векторов находится путем геометрического построения. О сумме векторов, выраженной через координаты векторов речь пойдет в другой статье.

Правило треугольника

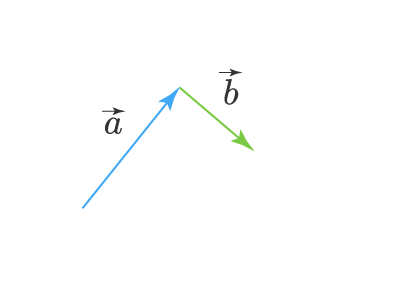
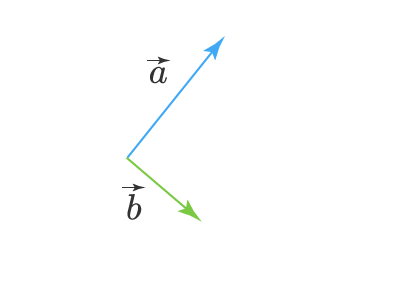
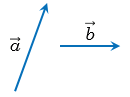
Вот нам даны два вектора a⃗vec{a} и b⃗vec{b}. Для того чтобы найти их сумму, пользуясь правилом треугольника, нужно чтобы начало одного из векторов находилось в точке конца другого вектора. То есть, чтобы точки начала одного вектора и конца другого вектора совпадали. Но что делать, если это не так? Для этого нужно параллельно перенести любой из векторов так чтобы это условие выполнялось. Например, пусть вначале векторы у нас расположены так:

Перенесем теперь вектор b⃗vec{b} параллельно самому себе так чтобы его начало совпало с концом вектора a⃗vec{a}. Получим:

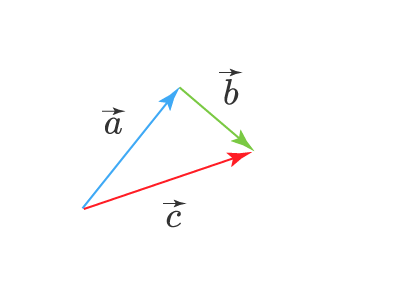
Теперь, чтобы найти сумму этих векторов, нужно провести вектор (стрелку) из начала вектора a⃗vec{a} в конец вектора b⃗vec{b}. Получим вектор c⃗=a⃗+b⃗vec{c}=vec{a}+vec{b}:

Правило параллелограмма

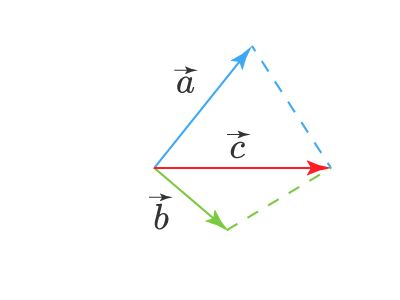
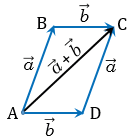
Решим ту же задачу вторым способом. Для этого нам нужно сделать так чтобы векторы a⃗vec{a} и b⃗vec{b} исходили из одной точки, то есть, чтобы точки начала этих векторов совпали. Получим:

Теперь построим на этих двух векторах параллелограмм. Суммой векторов a⃗vec{a} и b⃗vec{b} будет вектор, совпадающий с диагональю этого параллелограмма, и начало этого суммарного вектора c⃗vec{c} будет совпадать с началом векторов a⃗vec{a} и b⃗vec{b}:

На самом деле, по своему смыслу, оба эти правила это одно и то же правило. Просто так уж вышло, что в зависимости от построения треугольника или параллелограмма, говорят о соответствующем правиле складывания векторов.

Сумма любого числа векторов

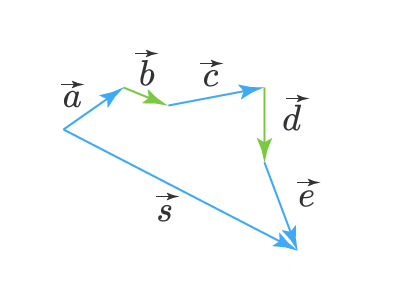
Складывать между собой можно не только два вектора, но и любое их количество. Для этого удобно воспользоваться правилом треугольника. Пусть у нас есть векторы a⃗,b⃗,c⃗,d⃗,e⃗vec{a}, vec{b}, vec{c}, vec{d}, vec{e}. Пусть мы перенесли параллельно векторы так, что начало каждого последующего вектора берет свое начало в конце предыдущего вектора, тогда сумма этих векторов, вектор s⃗vec{s} — это вектор с началом, совпадающим с началом первого вектора (вектора a⃗vec{a}) и концом, совпадающим с концом последнего вектора (вектора e⃗vec{e}):

Тест по теме “Сумма векторов”

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Векторы
Законы сложения векторов. Правило параллелограмма

Теорема

Доказательство

Дано: , и .

Доказать: 1⁰. + = + ; 2⁰. ( + ) + = + ( + ).

Доказательство:

1⁰. Пусть векторы и коллинеарны.

От произвольной точки А отложим векторы = и = , т.е. векторы и будут лежать на одной прямой и на той же прямой от точки А отложим векторы = и = .

+ = , + = , тогда , , при этом , так как модуль вектора — это длина отрезка, следовательно, . Поэтому точки С и С₁ совпадают, значит, = (по определению равных векторов), значит, + = + .

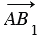
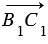
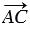
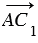
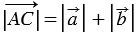
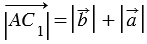
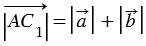
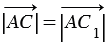
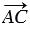
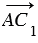
Пусть теперь векторы и не коллинеарны.

От произвольной точки А отложим векторы = и = и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы и сонаправлены, следовательно, = = (по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы и сонаправлены, следовательно, = = .

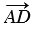
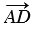
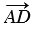
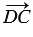
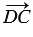
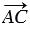
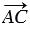
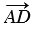
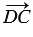
По правилу треугольника = + = + . Аналогично = + = + , поэтому + = + .

2⁰. От произвольной точки А отложим вектор = , от точки В — вектор = , а от точки С — вектор = .

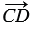
Применяя правило треугольника, получим:

( + ) + = ( + ) + = + = ,

+ ( + ) = + ( + ) = + = .

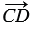
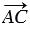
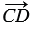
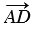
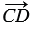
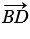
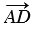
Следовательно, ( + ) + = + ( + ).

Теорема доказана.

Правило параллелограмма

Советуем посмотреть:

Понятие вектора

Равенство векторов

Откладывание вектора от данной точки

Сумма двух векторов

Сумма нескольких векторов

Вычитание векторов

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции

Векторы

Правило встречается в следующих упражнениях:

7 класс

Задание 784,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 802,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 808,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 906,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 907,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 909,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 8,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1050,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1067,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).

Проиллюстрируем сложение. Пусть даны вектора и , попытаемся найти вектор displaystyle vec{c}=vec{a}+vec{b} .

Способ 1. Метод сложения треугольником

Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора () и начало второго ( displaystyle vec{b} ) (рис. 1)

Рис. 1. Сложение векторов (правило треугольника)

Тогда вектор, соединяющий начальную точку первого вектора () и конец второго (), является вектором ( displaystyle vec{c} ).

Способ 2. Метод сложения параллелограммом

Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора () и начало второго ( displaystyle vec{b} ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.

Рис. 2. Сложение векторов (правило параллелограмма)

Тогда вектор, соединяющий общую начальную точку первого () и второго () векторов и общий конец данных векторов, является вектором суммы ( displaystyle vec{c} ).

Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.

Источник