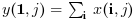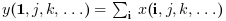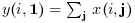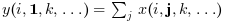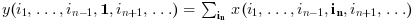Как найти сумму элементов массива scilab

Специальные матричные функции

Основные функции для работы с матрицами рассмотрены в статье Массивы в Scilab.
Другие полезные функции рассмотрены в статье Функции для решения задач линейной алгебры в Scilab

Ниже остановимся на специальных функциях: поиска минимального и максимального элементов, сортировки, объединения массивов в Scilab и т.д..

Задание матриц/векторов специального вида

Создаём матрицу из единиц: функция ones(n,m) в Scilab

Указываем число строк и число столбцов матрицы.

Задаём вектор-строк и вектор-столбец единиц

R = ones(1,3);  
C = ones(3,1); 

(
begin{matrix}
R = begin{pmatrix}
1 & 1 & 1
end{pmatrix} &
C = begin{pmatrix}
1 \ 1 \ 1
end{pmatrix}
end{matrix}
)

Задаём матрицу из единиц размерностью m на n

A = ones(3, 2);  
S = ones(2, 2); 

(
begin{matrix}
A = begin{pmatrix}
1 & 1 \
1 & 1 \
1 & 1
end{pmatrix} &
S = begin{pmatrix}
1 & 1 \
1 & 1
end{pmatrix}
end{matrix}
)

Задаём матрицу D из единиц, той же размерности, что и матрица A

A = [1 2 3;4 5 6];
D = ones(M);

(
begin{matrix}
A = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
D = begin{pmatrix}
1 & 1 & 1\
1 & 1 & 1
end{pmatrix}
end{matrix}
)

Создаём матрицу из нулей: функция zeros(n,m) в Scilab

Указываем число строк и число столбцов матрицы.

Задаём вектор-строк и вектор-столбец нулей

R = zeros(1,3);  
C = zeros(3,1); 

(
begin{matrix}
R = begin{pmatrix}
0 & 0 & 0
end{pmatrix} &
C = begin{pmatrix}
0 \ 0 \ 0
end{pmatrix}
end{matrix}
)

Задаём матрицу нулей размерностью m на n

A = zeros(3, 2);  
S = zeros(2, 2); 

(
begin{matrix}
A = begin{pmatrix}
0 & 0 \
0 & 0 \
0 & 0
end{pmatrix} &
S = begin{pmatrix}
0 & 0 \
0 & 0
end{pmatrix}
end{matrix}
)

Задаём матрицу D из нулей, той же размерности, что и матрица A

A = [1 5 4;3 2 6];
D = zeros(M);

(
begin{matrix}
A = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
D = begin{pmatrix}
0 & 0 & 0\
0 & 0 & 0
end{pmatrix}
end{matrix}
)

Создаём единичную матрицу: функция eye(n,m) в Scilab

Указываем число строк и число столбцов матрицы.

Задаём единичную матрицу нулей размерностью m на n

A = eye(3, 3);  
B = eye(3, 4); 
V = eye(3,1)

(
begin{matrix}
A = begin{pmatrix}
1 & 0 & 0\
0 & 1 & 0\
0 & 0 & 1
end{pmatrix} &
B = begin{pmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 1 & 0
end{pmatrix} &
V = begin{pmatrix}
1 \
0 \
0
end{pmatrix}
end{matrix}
)

Задаём единичную матрицу D, той же размерности, что и матрица A

A = [1 2;4 5];
D = eye(M);

(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
4 & 5
end{pmatrix} &
D = begin{pmatrix}
1 & 0 \
0 & 1
end{pmatrix}
end{matrix}
)

Создаём случайную матрицу/вектор: функция rand(n,m, key) в Scilab

Указываем число строк и число столбцов матрицы и необязательный параметр key — это символьная переменная с помощью которой можно задать тип распределения случайной величины (по умолчанию равномерное — ‘uniform’: гауссовское — ‘normal’).

Задаём матрицу m на n случайных чисел

A = rand(3, 2);  
V = rand(3,1,'normal');

(
begin{matrix}
A = begin{pmatrix}
0.2113249 & 0.3303271\
0.7560439 & 0.6653811 \
0.0002211 & 0.6283918
end{pmatrix} &
V = begin{pmatrix}
-0.7335813 \
0.1034169 \
0.8915736
end{pmatrix}
end{matrix}
)

Создаём квадратную матрицу с элемнтами V на k-oй диагонали: функция diag(V[,k]) в Scilab

Задаём вектор V и указываем, на какой диагонали его разместить.

V = [1 2 3];
A = diag(V);  

(
begin{matrix}
A = begin{pmatrix}
1 & 0 & 0\
0 & 2 & 0\
0 & 0 & 3
end{pmatrix}
end{matrix}
)

V = [1 2 3];
В = diag(V, 1);
С = diag(V, -1);  

(
begin{matrix}
B = begin{pmatrix}
0 & 1 & 0 & 0\
0 & 0 & 2 & 0\
0 & 0 & 0 & 3 \
0 & 0 & 0 & 0
end{pmatrix} &
C = begin{pmatrix}
0 & 0 & 0 & 0\
1 & 0 & 0 & 0\
0 & 2 & 0 & 0\
0 & 0 & 3 & 0
end{pmatrix}
end{matrix}
)

Создаём нижне-треугольную матрицу: функция tril(A[,k]) в Scilab

Указывавем матрицу, из которой будем формировать нижне-треугольную и диагональ, с которой начинать

A = [1 1 1; 2 2 2; 3 3 3];
B1 = tril(A);
B2 = tril(A, 1);
B3 = tril(A, -1);

(
begin{matrix}
A = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_1 = begin{pmatrix}
1 & 0 & 0\
2 & 2 & 0 \
3 & 3 & 3
end{pmatrix} &
B_2 = begin{pmatrix}
1 & 1 & 0\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_3 = begin{pmatrix}
0 & 0 & 0\
2 & 0 & 0 \
3 & 3 & 0
end{pmatrix}
end{matrix}
)

Создаём верхне-треугольную матрицу: функции triu(A[,k]) в Scilab

Указывавем матрицу, из которой будем формировать верхне-треугольную и диагональ, с которой начинать

A = [1 1 1; 2 2 2; 3 3 3];
B1 = tril(A);
B2 = tril(A, 2);
B3 = tril(A, -1);

(
begin{matrix}
A = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_1 = begin{pmatrix}
1 & 1 & 1\
0 & 2 & 2 \
0 & 0 & 3
end{pmatrix} &
B_2 = begin{pmatrix}
0 & 0 & 1\
0 & 0 & 0 \
0 & 0 & 0
end{pmatrix} &
B_3 = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
0 & 3 & 3
end{pmatrix}
end{matrix}
)

Создаём разреженную матрицу: функции ( sparse(V_1, V_2) ) в Scilab

( V_1 ) — вектор координат(строка, столбец) ненулевых эелемнтов
( V_2 ) — вектор значений ненулевых эелемнтов

A = sparse([1 2; 2 5; 3 1; 3 4], [8 9 15 11]);
full(A);

(
begin{matrix}
A = begin{pmatrix}
0. & 8. & 0. & 0. & 0.\
0. & 0. & 0. & 0. & 9.\
15. & 0. & 0. & 11. & 0.
end{pmatrix}
end{matrix}
)

Функции преобразования матриц/векторов

Изменяем размер матрицы: функция matrix(A [,n,m]) в Scilab

A = [1 2;3 4;5 6];  

( A = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6
end{pmatrix} )

Указываем матрицу, которую меняем, потом число строк и число столбцов новой матрицы.

B1 = matrix(A,2,3);
B2 = matrix(A,3,2);
B3 = matrix(A,1,6);
B4 = matrix(A,6,1);

(
begin{matrix}
B_1 = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
B_2 = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6
end{pmatrix} &
B_3 = begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6
end{pmatrix} &
B_4 = begin{pmatrix}
1 \ 3 \ 4 \ 5 \ 6
end{pmatrix}
end{matrix}
)

Конкатенация (склейка) матриц/векторов: функция cat(n, A, B) в Scilab

Склеиваем матрицы по строкам, т.е. друг под другом

A = [1 2; 3 4];
B = [5 6; 7 8];
C = cat(1, A, B);  

(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 \
7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6 \
7 & 8
end{pmatrix}
end{matrix}
)

Объединяем вектора (массивы) по строкам, т.е. друг под другом

A = [1 2 3 4];
B = [5 6 7 8];
C = cat(1, A, B);  

(
begin{matrix}
A = begin{pmatrix}
1 & 2 & 3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 & 7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 3 & 4\
5 & 6 & 7 & 8
end{pmatrix}
end{matrix}
)

Склеиваем матрицы по столбцам, т.е. друг за другом

A = [1 2; 3 4];
B = [5 6; 7 8];
C = cat(2, A, B);  

(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 \
7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 5 & 6 \
3 & 4 & 7 & 8
end{pmatrix}
end{matrix}
)

Объединяем вектора (массивы) по столбцам, т.е. друг за другом

A = [1 2 3 4];
B = [5 6 7 8];
C = cat(2, A, B);  

(
begin{matrix}
A = begin{pmatrix}
1 & 2 & 3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 & 7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8
end{pmatrix}
end{matrix}
)

Сортируем элементы матриц/векторов: функция gsort(A,option,direction) в Scilab

option — символьная строка. Она задаёт тип требуемой сортировки:
‘r’ — сортируется каждый столбец A
‘c’ — сортируется каждая строка A
‘g’ — сортируются все элементы A. Это значение по умолчанию.

direction — символьная строка. Она задаёт направление сортировки:
‘i’ устанавливает порядок возрастания,
‘d’ устанавливает порядок убывания (по умолчанию).

A = [7 2; 4 10];

B1 = gsort(A, 'r');
B2 = gsort(A, 'c');
B3 = gsort(A); 
B4 = gsort(A, 'c', 'i');

(
begin{matrix}
A = begin{pmatrix}
7 & 2 \
4 & 10
end{pmatrix} &
B_1 = begin{pmatrix}
7 & 10 \
4 & 2
end{pmatrix} &
B_2 = begin{pmatrix}
7 & 2 \
10 & 4
end{pmatrix} &
B_3 = begin{pmatrix}
10 & 4 \
7 & 2
end{pmatrix} &
B_4 = begin{pmatrix}
2 & 7 \
4 & 10
end{pmatrix}
end{matrix}
)

Функции вычисления различных характеристик матриц/векторов

Определяем размер матриц/векторов: функция size(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — число строк матрицы A
‘c’ — число столбцов матрицы A.

A = [7 2 1; 3 4 10];
  
[m, n] = size(A);
  
m = size(A, 'r');
n = size(A, 'c');

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
m = 2 & n = 3
end{matrix}
)

Найдём сумму элементов массива/матрицы: функция sum(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — поэлементную сумму строк матрицы A. Возвращает строку.
‘c’ — поэлементную сумму столбцов матрицы A. Возвращает столбец.

Если option отсутствует, то возвращается сумма всех элементов.

A = [7 2 1; 3 4 10];
  
R = sum(A, 'r');
V = sum(A, 'c');
S = sum(A);

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
10 & 6 & 11
end{pmatrix}&
V = begin{pmatrix}
10 \ 17
end{pmatrix} &
S = 27
end{matrix}
)

Найдём произведение элементов массива/матрицы: функция prod(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — поэлементное произведение строк матрицы A. Возвращает строку.
‘c’ — поэлементное произведение столбцов матрицы A. Возвращает столбец.

Если option отсутствует, то возвращается произведение всех элементов.

A = [7 2 1; 3 4 10];
  
R = sum(A, 'r');
V = sum(A, 'c');
P = sum(A);

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
21 & 8 & 10
end{pmatrix}&
V = begin{pmatrix}
14 \ 120
end{pmatrix} &
P = 1680
end{matrix}
)

Найдём наибольший элемент массива/матрицы: функция max(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — наибольший элемент в каждом столбце матрицы A. Возвращает строку.
‘c’ — наибольший элемент в каждой строке матрицы A. Возвращает столбец.

Если option отсутствует, то возвращается наибольший элемент во всей матрице.

A = [7 2 1; 3 4 10];
  
R = max(A, 'r');
V = max(A, 'c');
M = max(A);

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
7 & 4 & 10
end{pmatrix}&
V = begin{pmatrix}
7 \ 10
end{pmatrix} &
M = 10
end{matrix}
)

Найдём наименьший элемент массива/матрицы: функция min(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — наименьший элемент в каждом столбце матрицы A. Возвращает строку.
‘c’ — наименьший элемент в каждой строке матрицы A. Возвращает столбец.

Если option отсутствует, то возвращается наименьший элемент во всей матрице.

A = [7 2 1; 3 4 10];
  
R = min(A, 'r');
V = min(A, 'c');
M = min(A);

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
3 & 2 & 1
end{pmatrix}&
V = begin{pmatrix}
1 \ 3
end{pmatrix} &
M = 1
end{matrix}
)

Найдём среднее значение массива/матрицы: функция mean(A,option) в Scilab

option — символьная строка. Она возволяет определить:
‘r’ — среднее значение в каждом столбце матрицы A. Возвращает строку.
‘c’ — среднее значение в каждой строке матрицы A. Возвращает столбец.

Если option отсутствует, то возвращается среднее значение всей матрицы.

A = [7 2 1; 3 4 10];
  
R = mean(A, 'r');
V = mean(A, 'c');
M = mean(A);

(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
5 & 3 & 5.5
end{pmatrix}&
V = begin{pmatrix}
3.3333 \ 5.6666
end{pmatrix} &
M = 4.5
end{matrix}
)

Основные функции для работы с матрицами рассмотрены в статье Массивы в Scilab.

МАТРИЧНЫЕ
ВЫЧИСЛЕНИЯ И ЧИСЛЕННЫЙ АНАЛИЗ В SCILAB

1. Функции и
операции по обработке матриц

В системе SciLab
основной единицей данных является
матрица, поэтому система имеет обширный
набор стандартных функций и операций
по обработке матриц, который позволяет:

— формировать новые
матрицы стандартного вида;

— выполнять матричные
арифметические операции;

— вычислять матричные
характеристики и математические функции.

Для формирования
новых матриц стандартного вида применяются
следующие системные функции:

rand(M,N)
– формирует прямоугольную матрицу
размерностью M×N,
элементами которой являются случайные
числа в интервале (0.0; 1.0), функция rand
без параметров формирует одно случайное
число в том же интервале.

ones(M,N)
формирует единичную матрицу размерностью
M×N.

zeros(M,N)
формирует матрицу размерностью M×N,
состоящую из нулей.

diag(V)
создает диагональную матрицу, в которой
элементы вектора V
являются элементами главной диагонали.

Матричные
арифметические операции представлены
следующими:

A+B
, A—B
матричное сложение и вычитание. Оба
операнда этой операции должны иметь
одинаковую размерность, если они являются
матрицами. Один из операндов может выть
скалярной величиной.

A*B
матричное умножение. Операция выполняется
по правилам матричного умножения, число
столбцов матрицы A
должно быть равно числу строк матрицы
B.

A
B
левое деление матриц. Осуществляет
решение системы линейных алгебраических
уравнений A*X=B.
Число столбцов А должно быть равно числу
строк В.

A
/ B
правое деление матриц. Осуществляет
решение системы линейных алгебраических
уравнений X*A=B.

Х ^ Р
возведение матрицы в степень. Эта
операция при скалярном значении Р
возводит квадратную матрицу Х в степень
Р. Если Х – скалярная величина, а Р –
квадратная матрица, то Х^Р возводит Х в
матричную степень Р. Эта операция
является ошибочной, если оба операнда
– матрицы.

SciLab
существуют матричные операции, которые
выполняются над каждым элементом
матрицы, это такие операции, как:

.*
поэлементное матричное умножение.

.
поэлементное левое деление матриц.

. /
поэлементное правое деление матриц.

.^
поэлементное возведение матрицы в
степень.

Оба операнда этих
операций должны иметь одинаковую
размерность, или один из них должен
являться скалярной величиной.

Операция «апостроф»
′
вычисляет комплексно сопряженную
транспонированную матрицу.

Операция «точка
апостроф» .′
вычисляет транспонированную матрицу.

Ниже приведены
примеры выполнения матричных арифметических
операций.

Система содержит
стандартные функции, позволяющие
вычислять различные характеристики
матриц:

det(A)
вычисляет определитель матрицы;

trace(A)
вычисление следа матрицы;

rank(A)
вычисление ранга матрицы;

inv(A)
вычисление обратной матрицы.

Ниже приведены
примеры вычисления этих характеристик
для матриц А и В.

Над массивами
можно выполнять различные операции,
заданные системными функциями.

max(А)
вычисление максимального элемента
массива;

min(А)
вычисление минимального элемента
массива;

sum(A)
вычисление суммы элементов массива;

prod(A)
вычисление произведения элементов
массива;

mean(A)
вычисление среднего значения элементов
массива.

Порядок применения
этих функций и результаты их выполнения
рассмотрены на примерах.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #