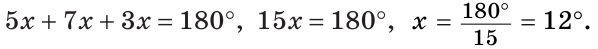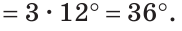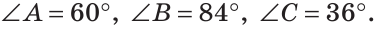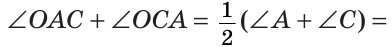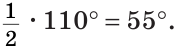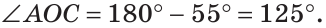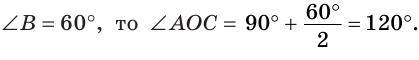Сумма углов треугольника равна (180°).
Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника (KLM) все углы острые.
У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
У треугольника (KLM) один угол тупой.
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
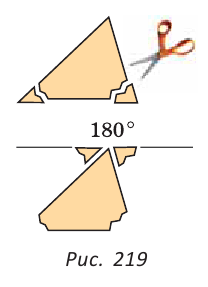
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 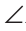
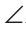
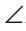
Доказательство:
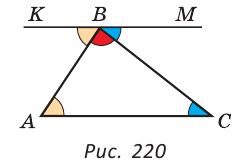
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 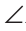
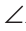
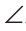
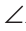





Следствия.
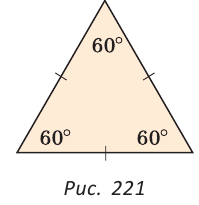
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
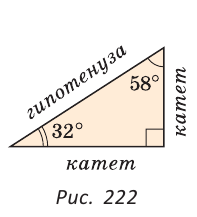
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
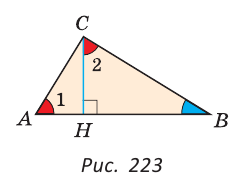
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
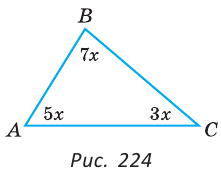
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 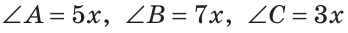
Так как сумма углов треугольника равна 180°, то
Тогда 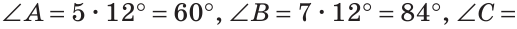
Ответ:
Пример:
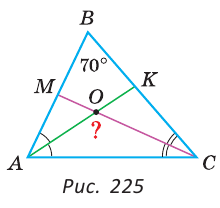
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Ответ: 125°.
Замечание. Если 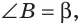
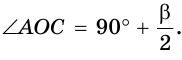
Пример:
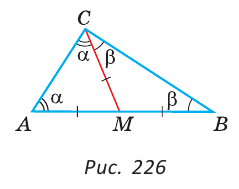
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 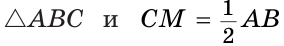
Докажем, что























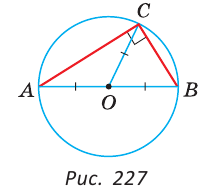
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
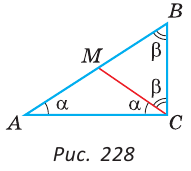
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Сумма углов треугольника
Доказательство теоремы:
Нарисуем треугольник. Через одну из его вершин проведем прямую, параллельную противоположной стороне, и найдем на рисунке равные углы.
Угол 1 равен углу BAC, они накрест лежащие. Угол 2 равен углу ACB, они тоже накрест лежащие.
Сумма угла 1, угла ABC и угла 2 составляет развернутый угол.
A развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Разберем задачи ЕГЭ и ОГЭ, в которых фигурирует сумма углов треугольника.
Заметим, что они похожи друг на друга. Одна и та же задача на тему «Сумма углов треугольника» может встретиться и на ОГЭ, и на ЕГЭ по математике. И уровень сложности заданий по этой теме в ЕГЭ и ОГЭ примерно одинаковый.
Задачи ЕГЭ по теме: Сумма углов треугольника
Задача 1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Решение:
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х.
Получим уравнение:
и найдем x = 17.
Тогда .
Ответ: 51.
Обратите внимание, что это даже не геометрия, а алгебра. Мы составили уравнение и решили его.
Задача 2.
Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Решение:
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны
.
Ответ: 41.
Задача 3.
На рисунке угол 1 равен , угол 2 равен
, угол 3 равен
. Найдите угол 4. Ответ дайте в градусах.
Решение:
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол 5.
Он равен
Тогда
Угол 4, смежный с углом 7 равен
Ответ:
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Задача 4.
Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Решение:
Пусть углы треугольника равны 2x, 3x и 4x. Запишем, чему равна сумма углов этого треугольника.
Тогда
Здесь мы тоже составили уравнение и решили его. Так же, как на уроках алгебры.
Ответ: 40.
Задача 5. В треугольнике ABC проведена биссектриса AL, угол ALC равен , угол ABC равен
. Найдите угол ACB. Ответ дайте в градусах.
Решение:
ALC — внешний угол
и он равен сумме двух внутренних углов, не смежных с ним. Значит,
.
AL — биссектриса , а это значит, что
.
По теореме о сумме углов треугольника получаем:
Ответ: 125.
Задача 6. В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, B=61
D=151
Найдите величину угла A. Ответ дайте в градусах.
Решение:
Если соединить точки B и D, получим два равных треугольника. Они равны по трем сторонам. В равных треугольниках напротив равных сторон лежат равные углы.
В треугольнике ABD сумма двух углов
Тогда , по теореме о сумме углов треугольника.
Ответ: 74.
Задача 7. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен . Найдите вписанный угол ACB. Ответ дайте в градусах.
Решение:
AC и BD — диаметры окружности. Значит, — равнобедренный, в нем
— как радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике:
.
Ответ: 28.
Задача 8. В треугольнике ABC AD — биссектриса, угол C равен , угол CAD равен
. Найдите угол B. Ответ дайте в градусах.
Решение:
AD — биссектриса, отсюда следует, что .
Тогда по теореме о сумме углов треугольника .
Ответ: 66.
Задача 9. В треугольнике ABC CD — медиана, угол C равен , угол B равен
. Найдите угол ACD. Ответ дайте в градусах.
Решение:
В треугольнике ABC угол C равен , угол B равен
, тогда угол A равен
.
CD — медиана. А медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Значит, .
Поэтому треугольник ADC равнобедренный и .
Ответ: 55.
Задача 10. В треугольнике ABC угол C равен , биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах
Решение:
В треугольнике ABC угол C равен , отсюда по теореме о сумме углов треугольника
.
Биссектрисы AD и BE пересекаются в точке O. Угол OAB — это половина угла CAB, угол OBA — это половина угла CBA. Теперь применим теорему о сумме углов треугольника к треугольнику AOB.
Ответ: 119.
Задача 11. В треугольнике ABC угол A равен , углы B и C — острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
Решение:
BD — высота тогда
— прямоугольный,
CE — высота тогда
— прямоугольный и
.
Углы и
— смежные, поэтому
.
Ответ: 124.
Задача 11. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
Решение:
Обозначим на рисунке вершины треугольника ABC, биссектрису CК и высоту CН. Биссектриса CК делит прямой угол на два угла по . Угол BCН равен разности углов BCК и КCН, то есть
.
Треугольники BCН и BAC подобны по двум углам. Значит, угол BAC равен углу BCН, то есть
Ответ: 31.
Задача 12. Острые углы прямоугольного треугольника равны и
. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Обозначим на рисунке медиану CМ и высоту CН.
Пусть и
. Высота CН разбивает прямоугольный треугольник на два треугольника, подобных исходному. Значит, угол BCН равен углу BAC, то есть
.
у которых углы равны т. е. угол C разбился на углы
и
Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Получили два равнобедренных треугольника, BCМ и ACМ. В треугольнике ACМ углы A и C равны 6 градусов каждый.
Тогда угол МCН между высотой и медианой равен:
Ответ: 78.
Задачи ОГЭ по математике по теме: Сумма углов треугольника.
Задача 13. В треугольнике два угла равны и
. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Сумма углов в треугольнике равна , поэтому
третий угол равен .
Ответ: 37.
Задача 14. Один из острых углов прямоугольного треугольника равен 34. Найдите его другой острый угол. Ответ дайте в градусах.
Решение:
Сумма острых углов прямоугольного треугольника равна . Поэтому второй острый угол равен:
.
Ответ: 56.
Задача 15.
В треугольнике ABC известно, что AB=BC, . Найдите угол BCA. Ответ дайте в градусах.
Решение:
В треугольнике ABC известно, что AB=BC. Значит, треугольник ABС равнобедренный, и углы при основании AС равны,
т.е. .
Ответ: 36.
Задача 16. В остроугольном треугольнике ABC проведена высота BH, . Найдите угол ABH. Ответ дайте в градусах.
Решение:
BH — высота , тогда
— прямоугольный, в нем
и
Используя теорему о сумме углов в треугольнике, найдем угол ABH:
Ответ: 53.
Задача 17. В треугольнике ABC угол C равен . Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол треугольника AВC при вершине C является смежным углом с углом ACB, а сумма смежных углов равна .
Значит, внешний угол треугольника ABC при вершине C равен: .
Ответ: 47.
Задача 18. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и . Найдите угол BOC. Ответ дайте в градусах.
Решение:
— равнобедренный,
.
— вписанный угол и опирается на дугу BC, а
— центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного опирающегося на ту же дугу,
.
Ответ: 155.
Задача 19. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ABC=123
. Найдите угол BOC. Ответ дайте в градусах.
Решение:
— равнобедренный треугольник, отсюда
.
— вписанный угол, он опирается на дугу BC, а
— центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу, значит,
.
Ответ: 57.
Задача 20. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен . Найдите угол ACB. Ответ дайте в градусах.
Решение:
AC и BD — диаметры, отсюда следует, что — равнобедренный,
— радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике
.
Ответ: 33.
Задача 21. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен . Ответ дайте в градусах.
Решение:
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. A это означает, что AB — диаметр. Угол, опирающийся на диаметр, равен , и треугольник ABC — прямоугольный. И если
, то второй острый угол этого треугольника равен:
Ответ: 15.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Сумма углов треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023