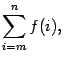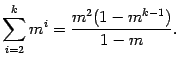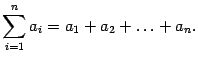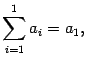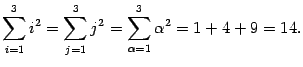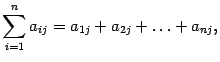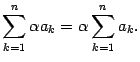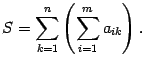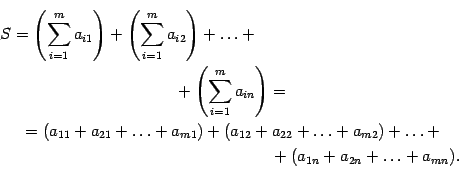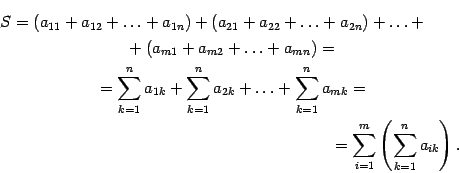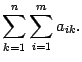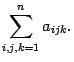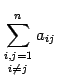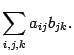Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Вёрстка:
Кирилл Климентьев
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Как найти сумму числового и функционального ряда
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ — математический знак суммы;
- ai — общий аргумент;
- i — переменная, правило для изменения каждого последующего аргумента;
- ∞ — знак бесконечности, «предел», до которого проводится суммирование.
Запись 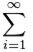
В соответствии с переменной i ряд можно записать развернуто:
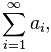
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
Сумма числового ряда – это предел частичных сумм Sn. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
Сначала найдем сумму числового ряда:
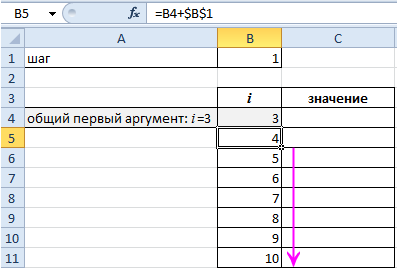
Теперь построим в Excel таблицу значений членов ряда:
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.
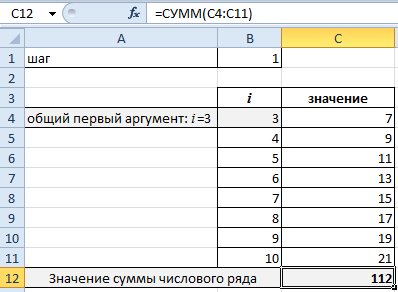
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.
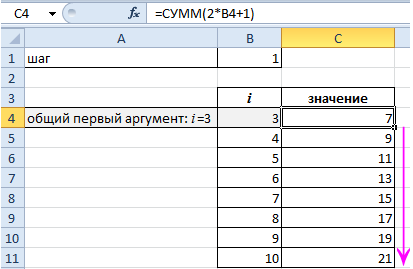
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x) 2 ; S3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
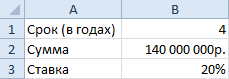
Исходные параметры для учебной задачи:
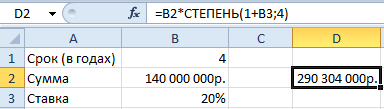
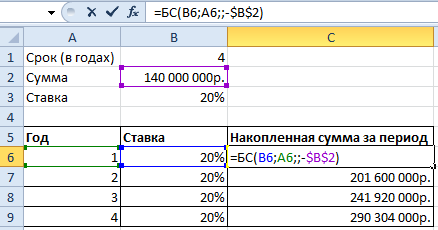
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
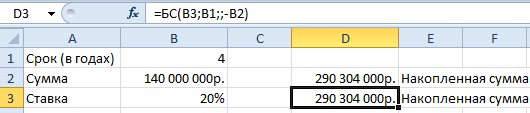
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
Результаты одинаковые, как и должно быть.
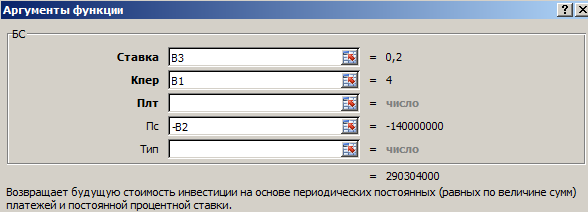
Как заполнить аргументы функции БС():
- «Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
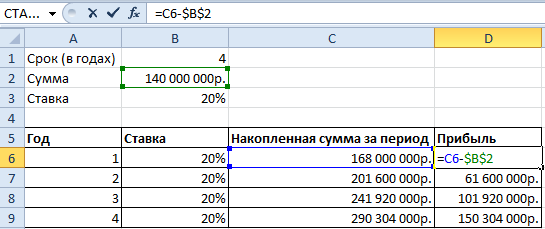
Сделаем еще один столбец, в котором отразим прибыль:
Как мы считали – в строке формул.
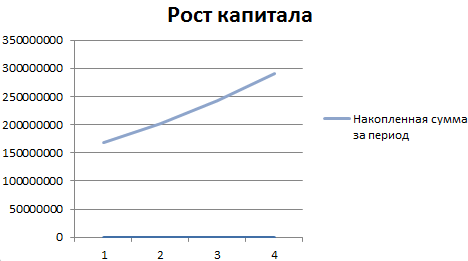
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:
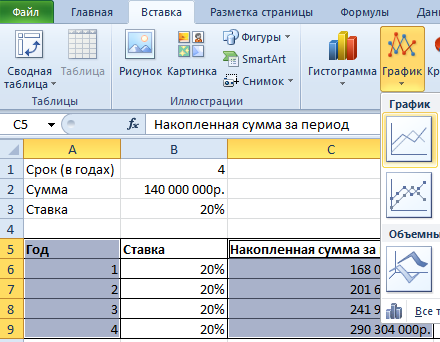
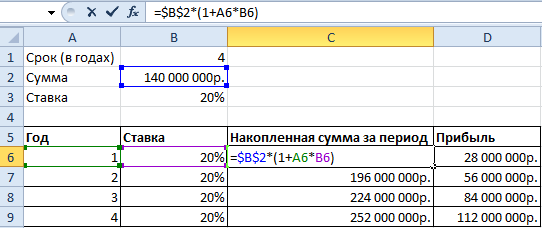
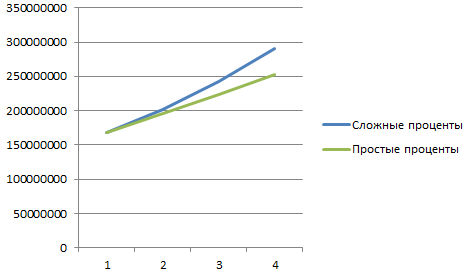
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
Добавим полученные значения в график «Рост капитала».
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Сумма ряда
Содержание:
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 


Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Заменяя 

Ответ.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://exceltable.com/funkcii-excel/nayti-summu-chislovogo-ryada
http://natalibrilenova.ru/summa-ryada/
План урока:
Действие сложение. Знак «+». Название компонентов действия сложения. Переместительное свойство сложения
Действие вычитание. Знак «–». Название компонентов действия вычитания
Взаимосвязь между действием сложения и действием вычитания
Действие сложение. Знак +
Название компонентов действия сложения. Переместительное свойство сложения
Добрый день! Готов к новому уроку? Сегодня у нас будет очень важное занятие. Мы получим самые драгоценные и сокровенные знания. Без этих знаний невозможно существование науки математики!
В таком сложном деле нам нужны помощники. Мы их найдем в сказочном лесу.
— Догадался? В этом лесу живут настоящие профессионалы по поиску драгоценностей и сокровищ. Это сказочные гномики.
Посмотри на них, какие они веселые и доброжелательные. Гномики улыбаются тебе и желают хорошего настроения на весь урок. Улыбнись им в ответ и давай приступим к занятию.
Гномики целый день работали в шахте. Они искали драгоценные камни.
Посмотри, сколько камней собрал гном Том и гном Тим. Посчитай.
Гном Том собрал 4 камня.
А гном Тим собрал 3 камня.
Чтобы не нести эту тяжесть в руках, они сложили все свои камни в тачку.
Теперь в тачке лежат и камни, которые собрал Том, и камни, которые собрал Тим. Давай-ка мы их все достанем и пересчитаем.
В тачке оказалось 7 камней.
Ого, как много! Как ты думаешь, почему?
Верно, потому что в тачку сложили камни оба гномика. А это всегда будет больше, чем у каждого по отдельности.
Итак, что сделали гномики?
Точно, они сложили свои камни вместе. В математике такое действие тоже называется сложение. Его суть в том, что элементы двух множеств объединяются в одно целое.
Смотри, множество камней Тома и множество камней Тима объединились в тачке в одно множество. При этом в объединенном множестве количество элементов становится больше.
Чтобы узнать результат сложения чисел, нужно пересчитать все элементы и первого, и второго множества вместе.
Гномики сложили камни вместе. А какие еще действия приводят к тому, что предметов становится больше?
Таких действий довольно много. Например, если в добавок к тому, что уже есть, кто-то:
- еще что-то даст или подарит;
- купит;
- принесет или привезет;
- смастерит еще несколько предметов;
- еще кто-то придет или прилетит.
Любое действие, которое ведет к увеличению количества предметов, подразумевает выполнение действия сложения. Часто это действие еще называют «прибавление».
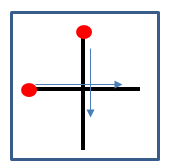
Чтобы записать действие сложение в виде математического выражения, используется специальный знак. Знак сложения выглядит так.
Посмотри, в этом знаке тоже произошло объединение: две палочки соединились в одно целое. Этот знак называется «плюс».
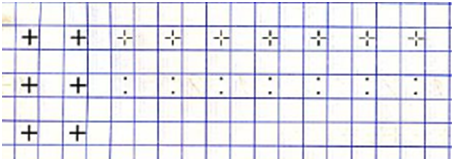
Посмотри, как знак «плюс» пишется в тетради.
Порядок написания следующий.
- Начинаем чуть ниже середины верхней границы клетки. Ведем прямую линию вниз и останавливаемся, немного не дописав до середины нижней границы клетки.
- Вторую линию начинаем писать чуть правее середины левой границы клетки. Ведем ее вправо и останавливаемся, немного не дописав до середины правой границы клетки.
Потренируйся писать знак плюс в тетради.
Теперь разберемся, как именно надо составлять математическое выражение, описывающее действие сложения. Давай вспомним, что было сначала.
Том собрал 4 камня и Тим собрал 3 камня.
Они вместе высыпали свои камни в тачку, т.е. объединили их. Поэтому мы ставим между числами знак «+».
В результате объединения все камни оказались в тачке. Мы их все пересчитали – в тачке 7 камней. Их ровно столько, сколько было у обоих гномиков вместе. Поэтому между левой и правой частью выражения нужно поставить знак равенства «=».
В тетради надо записать так.
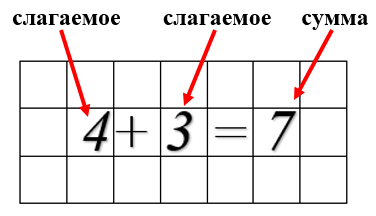
Теперь я расскажу, как называются компоненты действия сложения. Числа, которые обозначают количество элементов в каждом отдельном множестве, называются слагаемые. А число, которое обозначает результат, полученный при объединении этих множеств, называется сумма.
Поскольку левая сторона записи равна правой, то и само выражение тоже называют «сумма». Читают так «сумма чисел 4 и 3».
Поэтому, когда говорят «найди сумму», нужно выполнить действие сложение.
Итак, наше выражение можно прочитать несколькими способами:
- Четыре плюс три равно семь.
- К четырем прибавить три получим семь.
- Первое слагаемое – четыре, второе слагаемое – три, а сумма – семь.
- Сумма чисел четыре и три равна семи.
Идем дальше. Нам нужно выучить очень важное правило для действия сложения. Давай вернемся к нашим гномикам. Ты же помнишь, что каждый из них положил свои камни в тачку и потом мы их посчитали вместе, т.е. нашли сумму. Как ты думаешь, кто из гномиков первый положил камушки в тачку?
Мы записали, что первое слагаемое четыре. Получается, что первым был гномик Том, а потом гномик Тим.
Теперь давай представим, что порядок был другой. Сначала в тачку положил свои камушки Тим, а потом Том. Значит первое слагаемое – это три, а второе – четыре. Изменится ли от этого общее количество камней в тачке, т.е. наша сумма?
Теперь в тачке три камня Тима и четыре камня Тома. Посчитай их вместе.
Всего камней семь. Ровно столько же, сколько был и первый раз.
Получается, что не важно, кто из гномиков положил камушки первый, а кто второй. Их общее количество не меняется. Значит, сумма не меняется.
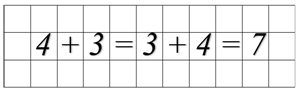
Посмотри. И четыре плюс три будет семь, и три плюс четыре тоже будет семь.
В математике это называется переместительное свойство сложения. Оно звучит так: от перестановки слагаемых местами сумма не изменяется. Запишем.
Это переместительное свойство очень пригодится тебе при изучении таблиц сложения. Запомни его!
Чтобы закрепить все, что мы узнали о действии сложения, потренируемся составлять примеры по картинкам.
Посчитай, сколько синих фигур на картинке. Запиши.
Правильно, 3.
Теперь посчитай красные фигуры и запиши.
Их 2.
Нам нужно посчитать их вместе. Это подразумевает объединение всех фигур. А значит, надо выполнить действие сложение. Поэтому поставим между нашими числами знак «плюс».
3 + 2
Теперь нужно пересчитать ВСЕ фигуры ВМЕСТЕ. Сколько у тебя получится?
У меня вышло 5. Уверена, у тебя тоже. Запишем это, поставив сначала знак равенства.
3 + 2 = 5
Вот и все. Ничего сложного.
Теперь рассмотрим, как нужно решать примеры на сложение. Давай прочитаем это выражение.
2 + 4
Можно так «два плюс четыре».
Чтобы найти результат, нужно следовать алгоритму выполнения действия сложения.
- Посмотри, какой знак используется в выражении.
Это знак «плюс», значит нужно объединить, посчитать все вместе.
- Назови первое слагаемое и положи перед собой нужное количество кружочков (можно взять палочки, спички, кубики или любые другие предметы).
- Теперь назови второе слагаемое и положи необходимое количество кружочков рядом с предыдущими.
- Пересчитай все кружочки вместе и запиши полученный результат.
2 + 4 = 6
Вот и все. Теперь ты знаешь, что такое действие сложение, как называются компоненты сложения, а также как составлять и решать примеры, в которых нужно выполнить это действие.
Действие вычитание. Знак-
Название компонентов действия вычитания
Давай продолжим раскрывать тайны науки математики. Ведь есть еще одно очень важное математическое действие, с которым нам обязательно нужно познакомиться.
Итак, гномики закончили свою работу и возвращаются домой.
Дома их ждет Белоснежка.
Она приготовила для гномиков угощение – испекла пирожные. Посчитай, сколько их получилось.
У тебя тоже получилось девять пирожных? Значит, ты посчитал правильно!
Когда гномики пришли домой, каждый из них съел по пирожному. Помнишь, сколько было гномов у Белоснежки? Точно, семь. Они съели столько же пирожных, т.е. тоже семь.
Давай зачеркнем съеденные пирожные.
Мы видим, что осталось совсем мало – всего два пирожных. Наверное, они достанутся Белоснежке.
В математике действие, которое ведет к уменьшению количества предметов, называется вычитание. Его смысл в следующем. Из целого множества удаляется его часть. В итоге остается меньше элементов, чем их было в целом множестве.
Чтобы узнать результат действия вычитания, нужно пересчитать элементы, которые остались.
Давай подумаем, в каких случаях предметов станет меньше. Пирожных стало меньше, потому что гномики съели часть из них. Еще могут быть такие ситуации:
- отдали;
- забрали;
- улетели (ушли, уехали);
- продали;
- использовали;
- сломали.
Для того, чтобы записать действие вычитания в виде математического выражения используют специальный знак. Знак вычитания выглядит так.
Он называется «минус».
В тетради знак «минус» пишется так.
Порядок написания знака «минус» следующий.
- Ставим ручку чуть правее середины левой границы клетки.
- Ведем горизонтальную прямую линию вправо.
- Останавливаемся, немного не доходя до середины правой границы клетки.
Потренируйся писать знак «минус» в тетради.
А теперь я расскажу, как составлять математическое выражение, которое описывает действие вычитание.
Вспомни, сколько пирожных было сначала?
Правильно, 9. Запиши.
9
Гномики съели пирожные и их стало меньше, поэтому ставим знак «минус».
9 –
Они съели 7 пирожных. Запишем это число.
9 – 7
Ставим знак равенства и запишем количество пирожных, которые остались. Их оставалось 2.
9 – 7 = 2
В тетради запись выглядит так.
Названия компонентов действия вычитания запомнить довольно легко.
- Первое число в результате вычитания станет меньше. Поэтому его называют уменьшаемое.
- Второе число показывает, сколько надо вычесть. Значит оно вычитаемое.
- В результате мы определяем какая разница между тем, что было и тем, что осталось. Поэтому результат действия вычитания называется разность.
Левая сторона этого выражения тоже называется разность.
Если в задании говорится, что нужно «найти разность чисел», значит, следует составить математическое выражение с действием вычитания.
Такое выражение можно прочитать по-разному.
- Из девяти вычесть семь будет два.
- Девять минус семь получим два.
- Уменьшаемое девять, вычитаемое семь, разность два.
- Разность чисел девять и семь равна двум.
Закрепим все, что ты узнал о действии вычитания и составим математическое выражение по такой картинке.
Посмотри, сколько всего было шариков у гномика сначала? Запиши.
Правильно, пять.
Что случилось с некоторыми шариками? Сколько таких шаров?
Верно, два шарика сдулись и у гномика шариков осталось меньше. Значит нужно написать «минус два».
5 – 2
Ставим знак равенства и пересчитаем, сколько осталось целых шариков.
Их три.
5 – 2 = 3
Вот мы и составили выражение.
А теперь разберемся, как нужно решать примеры на вычитание. Например, посчитаем, сколько будет:
6 — 4
Назови уменьшаемое. Выложи столько же кружочков. Их должно быть 6.
Теперь назови вычитаемое. Убери (отодвинь, зачеркни) четыре кружочка.
Пересчитай кружочки, которые остались, и ты узнаешь ответ. Запиши его после знака равенства.
6 – 4 = 2
Мы решили пример на вычитание. Теперь ты знаешь, что обозначает это математическое действие, как называются компоненты вычитания, и как нужно составлять и решать математические выражения с действием вычитания.
Взаимосвязь между действием сложения и действием вычитания
Итак, ты выучил два математических действия: сложение и вычитание. Одно из них используется при объединении предметов в единое множество, а другое при удалении из целого множества его части.
Ты вспомнил, что обозначает каждое действие?
Эти действия связаны между собой, но имеют противоположное значение. При сложении мы получаем больший результат, а при вычитании предметов становится меньше. Вот, например, представь, что у тебя было несколько конфет и тебе дадут еще пару штук. Что получится?
Правильно, у тебя конфет станет больше.
А если ты съешь несколько конфет? Что у тебя останется?
Правильно, у тебя останется меньше конфет.
А теперь давай проверим, какая именно взаимосвязь между действиями сложения и вычитания. Разберем одну ситуацию и составим по ней математическое выражение.
У Белоснежки День рождения. Гномики решили устроить для нее праздник. Посчитай, сколько их всех на картинке.
Правильно, их трое.
К Белоснежке на День рождения пришли зверята. Посчитай, сколько их.
Верно, пять зверят.
Подумай, какое действие мы должны использовать, чтобы составить выражение?
Ну конечно, действие сложение. Ведь теперь их всех вместе стало больше.
Было три, пришло еще пять. Посчитай, сколько теперь всех вместе.
Правильно, восемь.
Запишем в виде выражения.
3 + 5 = 8
3 – это первое слагаемое, оно показывает, сколько элементов было в первом множестве.
5 – это второе слагаемое, оно показывает, сколько элементов было во втором множестве.
8 – это сумма, она обозначает количество элементов в общем множестве.
Теперь на полянке и гномики с Белоснежкой (это наше первое множество), и зверята (это второе множество). Они все вместе.
Получается, что на празднике веселились 8 друзей. Когда праздник закончился, зверята ушли домой. Как ты думаешь, какое математическое действие надо использовать в этом случае?
Правильно, действие вычитание. Ведь зверята ушли и на полянке останется меньше друзей.
Итак, 5 зверят ушло. Кто остался? Сколько их?
Верно, остались гномики с Белоснежкой. Их 3.
Составим математическое выражение.
8 – 5 = 3
Мы видим, что если из общего множества (суммы) убрать элементы второго множества (второе слагаемое), то останутся только элементы первого множества (первое слагаемое).
А если было наоборот, из 8 друзей первыми с полянки ушли гномики с Белоснежкой (их 3). Кто на ней останется?
Правильно, останутся зверята. Их 5.
Посмотри, как это запишем.
8 – 3 = 5
Теперь мы из общего множества (суммы) убрали элементы первого множества (первое слагаемое) и остались только элементы второго множества (второе слагаемое).
Итак, у нас получается, что мы при сложении два множества объединяем в одно целое. А если из этого общего множества убрать какое-то одно из составляющих множеств, то останется другое.
В математике это правило взаимосвязи между компонентами сложения звучит так: если из суммы вычесть одно слагаемое, то получим другое слагаемое.
Мы видим, что в примере на сложение есть два слагаемых. Поэтому можно сделать следующий вывод: из одного математического выражения с действием сложения можно составить два выражения с действием вычитания.
8 – 3 = 5
8 – 5 = 3
Это очень важное правило, которое поможет тебе в дальнейшем быстро и легко учить таблицы вычитания.
А на сегодня все. Гномики помогли нам получить очень важные и ценные знания. Нужно обязательно поблагодарить их за это.
В материалах урока использованы кадры из а/ф «Белоснежка и семь гномов», 1937
Простые и двойные суммы
В математике часто приходится рассматривать суммы большого количества чисел или элементов некоторого множества с операцией сложения в нем, когда слагаемые имеют одинаковый вид и различаются лишь индексами, например суммы вида
Кратко такие суммы записывают следующим образом:
где символ ? — символ суммы: г — индекс суммирования.
Индекс суммирования можно обозначать любой буквой, т.е.
Множитель, не зависящий от индекса суммирования, можно выносить за знак суммы, т.е.
Часто также приходится суммировать слагаемые по двум индексам, каждый из которых независимо пробегает определенные значения. Это приводит к двойным суммам типа
При действиях с двойными суммами можно изменять порядок суммирования, т.е.
Отмеченное правило распространяется на случай суммирования по любому конечному числу индексов.
Перестановки и подстановки
Пусть дано конечное множество М, состоящее из п элементов. Элементы этого множества можно перенумеровать натуральными числами 1, 2, п. Поскольку нас не будут интересовать свойства элементов множества, то можно принять, что элементами множества М являются сами эти числа. Всякое расположение чисел 1, 2, . п в определенном порядке называют перестановкой из п чисел (или из п символов). В общем случае перестановку из п символов записывают в виде i . in, где каждое число is, s = 1, 2. п, есть одно из чисел 1, 2, . п и ни одно из этих чисел не повторяется.
Теорема 1.1. Общее количество различных перестановок из п символов равно n! = 1 • 2 • 3 •. • п.
> Действительно, в перестановке ii2—in за i можно принять любое из чисел 1, 2, . п. Таких возможностей всего п. При выбранном значении i за г 2 можно принять одно из п — 1 не совпадающих с i чисел. Значит, различных возможностей выбора пары символов i и %2 существует п(п — 1). Продолжая подсчет вариантов, через п шагов получим общее количество перестановок, равное п-(п —1)-. -3-2-1 = п. ?
Говорят, что числа г и j, стоящие в перестановке, составляют инверсию, или беспорядок, если i > j, в то время как i в этой перестановке стоит раньше (левее) числа j. Так, в перестановке 2 15 4 3 числа 2 и 1, 5 и 4, 4 и 3, 5 и 3 составляют инверсии.
Перестановку называют четной, если число всех инверсий в ней четно, и нечетной, если число всех инверсий в ней нечетно.
Подсчет числа инверсий в перестановке удобно проводить следующим образом. Сначала подсчитывают, сколько чисел в перестановке, больших единицы, стоит левее единицы. Затем подсчитывают, сколько чисел, больших двух, стоит левее двойки и т.д. Пусть левее единицы стоит к чисел, больших единицы, левее двух — чисел, больших двух и т.д. Наконец, пусть левее числа п — 1 стоит кп— чисел, больших п — 1. Тогда общее число инверсий в перестановке будет равно
Так, при подсчете числа инверсий в перестановке 3 2 1 5 4 получим: к = 2, к2 = 1, к’з = 0, = 1. Поэтому общее число инверсий в этой
перестановке равно 2 + 1 + 0+1 = 4, а перестановка является четной.
Перемену местами каких-либо двух символов в перестановке (не обязательно соседних) называют транспозицией этих символов. Транспозицию символов г и j в перестановке обозначают через (i,j). Транспозиция в перестановке из п символов приводит к другой перестановке из тех же символов. При помощи последовательности транспозиций можно перейти от одной перестановки из п символов к любой другой перестановке из тех же символов.
Теорема 1.2. Всякая транспозиция меняет четность перестановки.
О Рассмотрим случай транспозиции рядом стоящих символов г и j, т.е. случай транспозиции этих символов в перестановке вида Aij В, где А — группа символов, стоящих в перестановке слева от символа г, а В — группа символов, стоящих в перестановке справа от символа
j. Транспозиция (г, j) переводит данную перестановку в перестановку Aj iB. В обеих перестановках символ г составляет одни и те же инверсии с символами из групп А и В. То же самое справедливо и для символа j. Если в данной перестановке символы г и j не составляли инверсии, то в новой перестановке появится одна новая инверсия, т.е. число инверсий увеличится на единицу. Если же символы г и j в данной перестановке составляли инверсию, то в новой перестановке она пропадет, т.е. число инверсий уменьшится на единицу. В обоих случаях четность перестановки меняется.
Теперь рассмотрим общий случай, когда символы г и j в перестановке разделены группой из s символов (s > 0). Здесь перестановка имеет вид:
После транспозиции (г, j) эта перестановка примет вид:
Такое преобразование можно рассматривать как последовательность транспозиций, сперва символа г с символами ki, k,2, . ks, j, a затем символа j с символами ks, . ki, поэтому рассматриваемая транспозиция эквивалентна последовательности из 2 s + 1 транспозиций стоящих рядом символов. При этом четность перестановки будет меняться нечетное число 2 s + 1 раз, т.е. данная и полученная перестановки имеют разную четность. ?
Теорема 1.3. Число четных перестановок из п символов при п > 2 равно числу нечетных перестановок из п символов и составляет п!/2.
math serfer .narod.ru
где 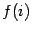
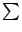
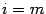
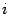
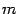
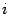
1) 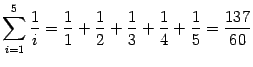
2) 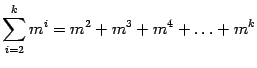
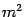
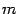
3) 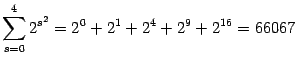
4) 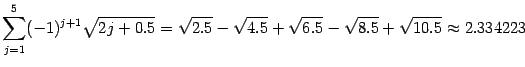
5) 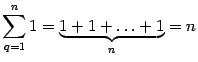
В курсе линейной алгебры чаще всего будут встречаться суммы вида 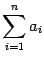
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:
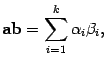 |
( 14 .2) |
где для трехмерного пространства 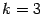
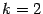
Для единообразия будем считать, что
и говорить, что это сумма, содержащая одно слагаемое.
в правой части никакой буквы />нет, значит, и результат от />не зависит.
Доказательство этого предложения предоставляется читателю.
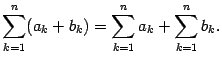 |
( 14 .3) |
Это предложение является частным случаем следующего утверждения.
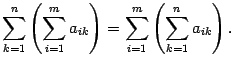 |
( 14 .4) |
Раскроем скобки в правой части этого равенства. Получим сумму элементов 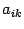
Заменив в этом равенстве 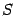
Нужно помнить, что двойная сумма означает сумму элементов 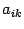
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
означает, что в сумму не включаются величины 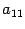
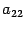
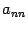
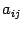
Иногда в записи суммы не указываются границы изменения индексов, например,
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Как поставить знак суммы в Ворде?
Если знак суммы нужен не сам по себе, как греческая буква, а как элемент математической формулы суммирования, то простые способы не подойдут, надо будет честно вставлять формулу: Вставка — Объект — Формула (Insert — Object — Equation) для версия 2003 или Вставка — Формула (Insert — Equation) для более поздних версий. Там есть инструменты для создания полноценной формулы суммы, с обозначениями индекса суммирования и верхнего предела и с автоматической подгонкой знака суммы под размер общего члена суммируемого ряда.
Знак суммы в ворде
Сумма в математике обозначается греческой буквой «сигма».
Очень часто вверху и внизу сигмы пишутся границы суммирования (начальное и конечное значение), поэтому для вставки этого символа в документ Ворд правильнее всего использовать встроенный редактор формул.
1) Сначала откройте вкладку (панель инструментов) «Вставка» и нажмите на «Формула».
Другой способ вставить формулу — это комбинация клавиш «Alt» и «+».
2) Отобразится панель «Конструктор», на которой можно найти различные структуры.
В нашем случае нам будет нужна структура, которая называется «Крупный оператор».
3) Если щёлкнуть по этой структуре левой кнопкой мыши, то появится выпадающее меню, в котором будет несколько вариантов знака суммы.
Можно выбрать сумму как без границ суммирования, так и с границами суммирования.
4) Щёлкаем левой кнопкой мыши на нужной сумме, она отобразится в документе.
5) Теперь остаётся в специальных пунктирных квадратиках написать границы суммирования (если это нужно) и то, что суммируется.
Все, ну или почти все знаки математических действий, можно найти в Таблице символов. Если и тех не хватает можно пополнить с сайта производителя Ворда.
Открываем вкладку Символы и в таблице находим знак суммы, нажимаем его и вставляем.
Есть несколько способов поставить знак суммы — греческой буквы сигма.
- Не самый удобный, но работающий способ. Поскольку речь идет о греческой букве, то можно установить греческий алфавит и ввести букву просто с клавиатуры;
- Выбираем меню Вставка — Символ — Символы — Другие символы. В открывшемся окне ищем необходимый значок. Для этого стоит выбрать набор Математические операторы. Выбираем, копируем и вставляем — ∑.
- Нажимаем Пуск — Программы — Стандартные — Служебные — Таблица символов. Аналогично ищем там необходимый значок, нажимаем его, выбираем Копировать и вставляем в нужное место;
- Вводим с помощью Alt и цифр на дополнительной клавиатуре. Нажимаем и удерживаем Alt, набираем на клавиатуре код — 931;
- Вводим с помощью кода и Alt + X. Набираем кода — 2211. Затем, не перемещая курсом и находясь на английской раскладке клавиатуры, нажимаем Alt и удерживаем, а затем нажимаем X и отпускаем обе кнопки. Такой метод работает в программах Office, но редко — в браузерах.
- Вводим с помощью кода и Alt + X — способ 2. Набираем кода — 03A3. Затем, не перемещая курсом и находясь на английской раскладке клавиатуры, нажимаем Alt и удерживаем, а затем нажимаем X и отпускаем обе кнопки. Результат следующий — Σ. Как видите, он несколько отличается.
Для того, чтобы вставить знак суммы Σ в текстовом редакторе Microsoft word, существует 2 способа:
- Надо пойти по панелям: Вставка — Символ — Другие символы. Там есть знак суммы Σ, код знака — 2211. При использовании нового символа он попадает в категорию «Ранее используемые символы» в меню «Символ». Там тоже можно брать нужные символы.
- Нажать на: Пуск — Все программы — Стандартные — Служебные — Таблица символов. Выбрать знак суммы, его код: U+03A3. Затем нажать «Выбрать» и «Копировать». Далее нужно вставить его в нужную строку в тексте.
Знак суммы Σ — это большая буква «Сигма» в греческом алфавите (большие греческие буквы).
В программе Ворд есть несколько видов символов, которые обозначают «знак суммы». Существует 5 вариантов написания. Ответ на Ваш вопрос зависит от того что нужно получить в итоге. Если символ нужен в качестве декоративного элемента, то есть реальный расчёт не требуется, то достаточно воспользоваться вставкой символа. Для этого ставим курсор в нужное место — нажимаем — Вставка — символы — ищем нужный нам значок.
А вот если знак суммы нужен для реально расчёта, то это уже другая история. Тогда обратился к формулам. Устанавливаем курсор в нужном месте при помощи мыши, ждём — Вставка — конструктор — выбираем формулу.






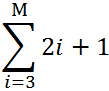
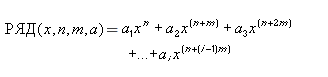




















 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем