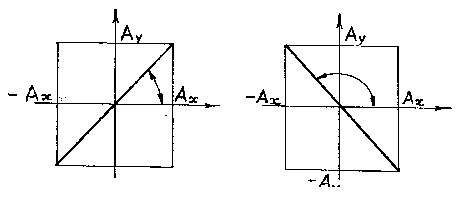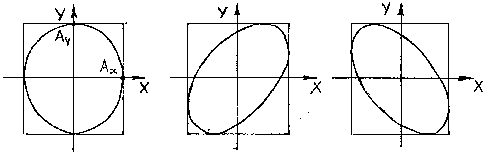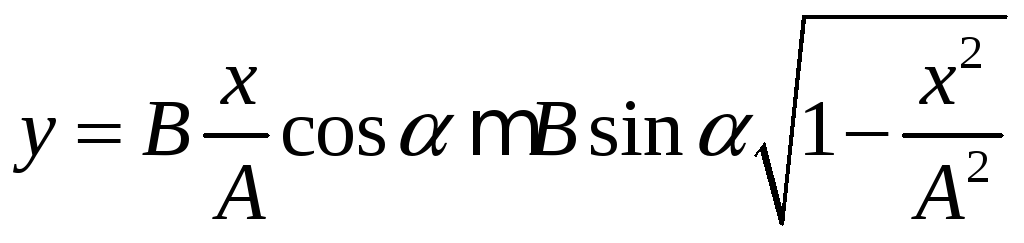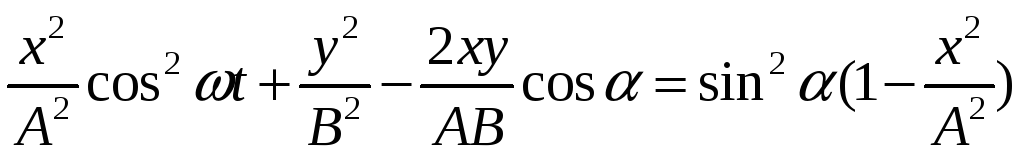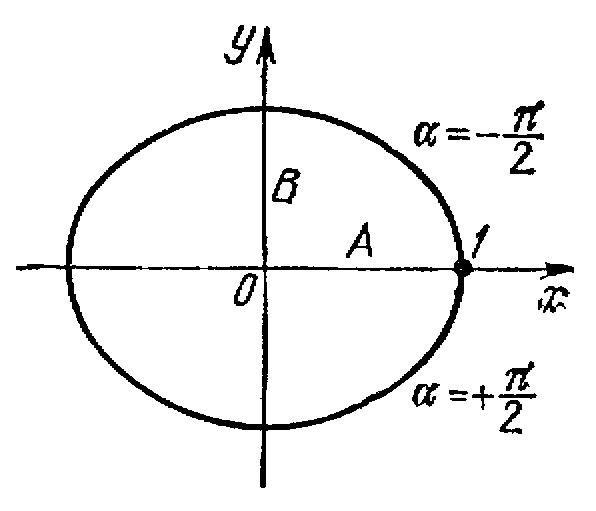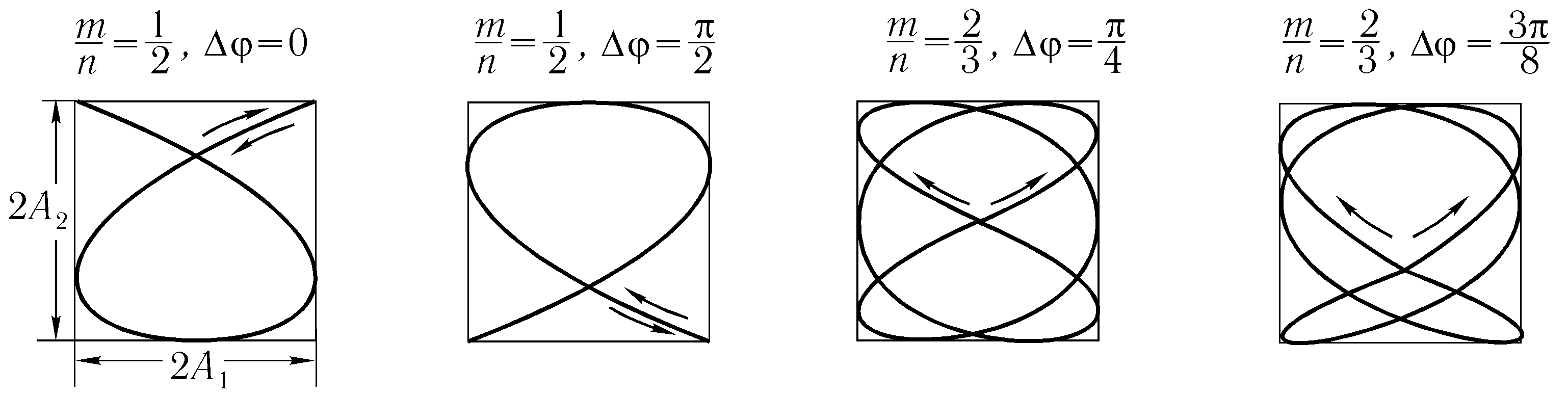Как найти сумму колебаний

2.1. Сложение гармонических колебаний одного направления

2.2. Сложение взаимно перпендикулярных колебаний

Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.

Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.

2.1. Сложение гармонических колебаний одного направления

1. Сложение двух колебаний одного направления (сонаправленных колебаний)

можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.

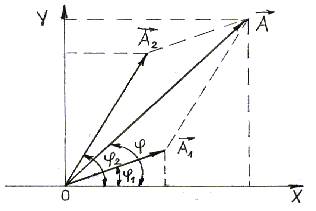
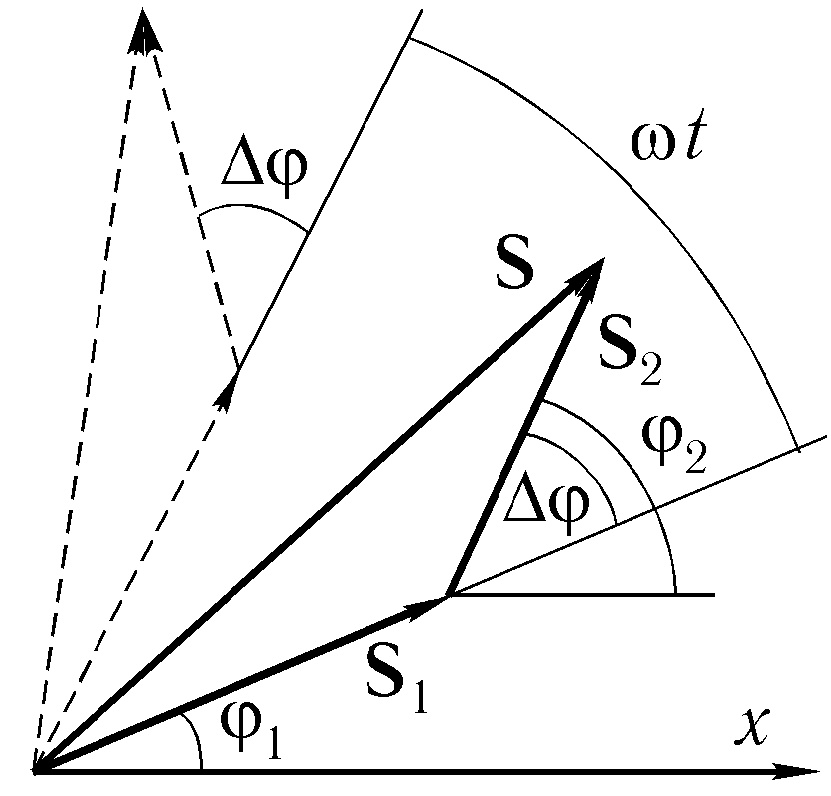
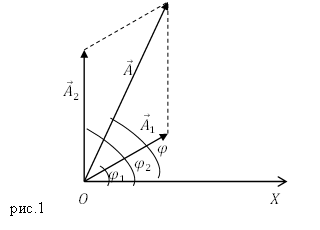
На Рисунке 2.1 показаны векторы амплитуд А₁(t) и А₂(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и . Сложение колебаний сводится к определению . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.

Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды и фаза .

Рисунок 2.1 – Сложение сонаправленных колебаний.

Величина вектора А(t) может быть найдена по теореме косинусов:

.

Фаза результирующего колебания задается формулой:

.

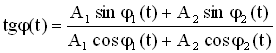
Если частоты складываемых колебаний ω₁ и ω₂ не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.

2. Два гармонических колебания x₁ и x₂ называются когерентными, если разность их фаз не зависит от времени:

.

Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты .

Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:

.

Начальную фазу результирующего колебания легко найти, если спроектировать векторы А₁ и А₂ на координатные оси ОХ и ОУ (см. Рисунок 9):

.

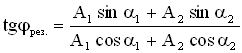
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .

3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.

Если , где n – любое целое неотрицательное число

(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При результирующая амплитуда равна нулю .

Если , то , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы , то .

4. Сложение сонаправленных колебаний с неравными, но близкими частотами.

Частоты складываемых колебаний не равны , но разность частот много меньше и ω₁, и ω₂. Условие близости складываемых частот записывается соотношениями .

Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k₁ и k₂.

Пусть амплитуды складываемых колебаний одинаковы, а начальные фазы равны нулю . Тогда уравнения складываемых колебаний имеют вид: , .

Результирующее колебание описывается уравнением:

.

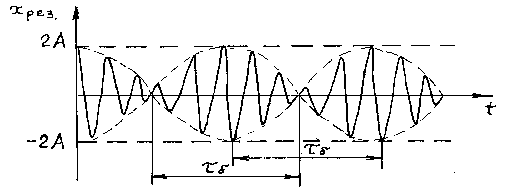
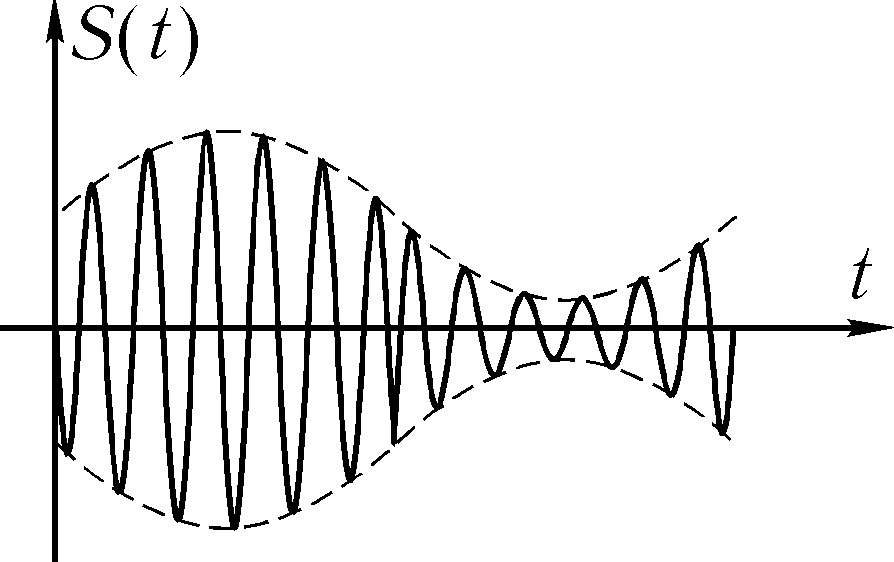
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой , где ω близка к частотам складываемых колебаний (ω₁ или ω₂). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.

Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости х_рез.при биениях показан на Рисунке 2.2.

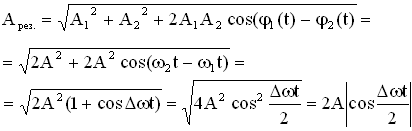
Рисунок 2.2 – Зависимость смещения от времени при биениях.

Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ_б, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:

.

Величина — период биений.

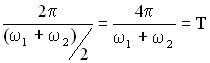
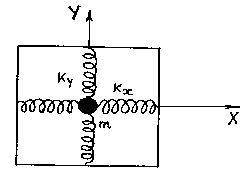
Величина есть период результирующего колебания (Рисунок 2.4).

1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.

Рисунок 2.3

Складываемые колебания имеют вид:

.

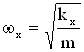
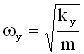
Частоты колебаний определяются как , , где , -коэффициенты жесткости пружин.

2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами , что соответствует условию (одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:

Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:

.

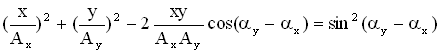
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.

а) Если , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:

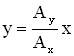
(Рисунок 2.3 а).

б) Если (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:

(Рисунок 2.3б).

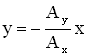
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω₀, амплитуда определяется соотношением:

.

Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:

(знак «плюс» – случай а, знак «минус» – случай б).

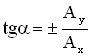
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным.

в) Если (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:

.

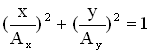
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны и (Рисунок 2.4 ).

Рисунок 2.4

Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний .

3. Сложение взаимно перпендикулярных колебаний с кратными частотами.

Складываются взаимно перпендикулярные колебания, частоты которых не равны , но , , где a и b – целые числа.

Периоды колебаний вдоль осей ОХ и ОУ соответственно равны и . Отношение периодов .

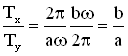
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, — замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.

Сложение колебаний. Векторные диаграммы. Биения.

Для
гармонических колебаний

;

При
условии равенства начальных фаз

;

Сумма
однонаправленных гармонических колебаний
одинаковой частоты.

Покажем,
что сумма есть гармоническое колебание
той же частоты

Сложение
координат дает

Преобразуя
тригонометрические соотношения по
известным формулам, получаем

+

После
алгебраических преобразований суммарная
координата приобретает вид

Вывод:
сумма гармонических колебаний есть
гармоническое колебание.

Сложение
гармонических колебаний с одинаковой
амплитудой а и разными частотами

=

=

Т.е.
рассматриваемое колебание – можно
рассмотреть как колебание с переменной
амплитудой- такое колебание носит
название биения

Метод
векторных диаграмм

где

Алгоритм:

1. построить
   векторы а, (характерные слагаемые
   колебания х для начального момента
   времени);

2. найти
   графическую сумму векторов;

3. спроецировать
   суммарный вектор на ось Ох, получить
   искомую сумму колебаний;

Если
все слагаемые с одной частотой, то фазы
будут отличаться только начальными
фазами. Суммарный вектор вращается с
такой же частотой.

Сложение колебаний Векторная диаграмма

Колебаниями
называются движения или процессы,
обладающие той или иной повторяемостью
во времени.

Сло­жение
нескольких гармонических колебаний
одного направления и одинаковой частоты
становится нагляд­ным,
если изображать колебания графически
в виде векторов на плоскости. Полученная
таким способом схема называется векторной
диаграммой.

Возьмем
ось, вдоль которой будем откладывать
колеблющуюся величину
x.
Из взятой на оси точки О
отложим вектор длины
A,
образующий с осью угол α.
Если привести этот вектор во вращение
с угло­вой скоростью ω₀,
то проекция конца вектора будет
перемещать­ся по оси x
в пределах от —А до
+A,
причем координата этой проекции будет
изменяться со временем по закону

Следовательно,
проекция конца вектора на ось будет
совершать гармонические колебания с
ам­плитудой, равной длине вектора, с
круговой частотой, равной угловой
скорости вращения вектора, и с на­чальной
фазой, равной углу, образуемому вектором
с осью в начальный момент времени.

Таким
образом, гармоническое колебание может
быть задано с помощью вектора, длина
которого рав­на амплитуде колебания,
а направление образует с осью x
угол, равный начальной фазе колебаний.

Рассмотрим
сложение двух гармонических коле­баний
одного направления и одинаковой частоты.
Результирующее колебание
будет суммой колеба­ний
х₁
и x₂,
которые определяются
функциями

,

(1)

Представим
оба колебания с помощью векторов A₁и
А₂.
Построим по правилам сложения векторов
результирующий вектор А.
На рисунке вид­но,
что проекция этого вектора на ось x
равна сум­ме проекций
складываемых векторов:

П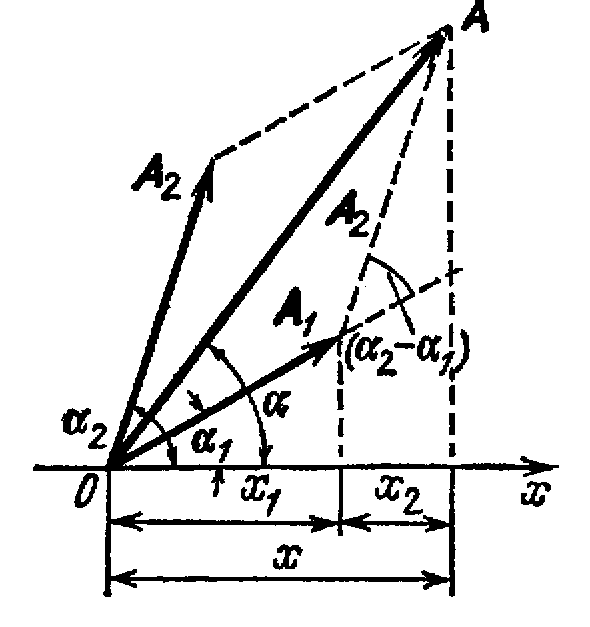оэтому,
вектор A
представляет собой
резуль­тирующее колебание. Этот вектор
вращается с той же угловой скоростью
ω₀,
как и векторы А₁
и А₂,
так что сумма x₁
и х₂
является гармоническим
колебанием с частотой (ω₀,
амплитудой A
и начальной фа­зой
α.
Используя теорему косинусов
получаем, что

(2)

Также,
из рисунка видно, что

(3)

Представление
гармонических колебаний с помощью
векторов позволяет заменить сложение
функций сложением векторов, что
значительно проще.

Сложение
колебаний во взаимно перпендикулярных
направлениях.

Представим
две взаимно перпен­дикулярные векторные
величины x
и y,
изменяющие­ся со
временем с одинаковой частотой ω
по гармони­ческому закону, то

(1)

Где
e_x
и e_у
— орты координатных
осей x
и y,
А и B
— амплитуды колебаний.
Величинами x
и у
может быть, например,
смещения материальной точки (частицы)
из положения равновесия.

В случае колеблющейся
частицы величины

,

(2)

определяют
координаты частицы на плоскости xy.
Частица будет двигаться
по некоторой траектории, вид которой
зависит от раз­ности фаз обоих
колебаний. Выражения (2) пред­ставляют
собой заданное в параметрической форме
уравнение этой траектории. Чтобы получить
уравне­ние траектории в обычном виде,
нужно исключить из уравнений (2) параметр
t.
Из первого уравне­ния
следует, что

(3) Соответственно

(4)

Развернем косинус
во втором из уравнений (2) по формуле для
косинуса суммы:

Подставим
вместо cos
ωt
и sinωt
их значения (3) и (4):

Преобразуем это
уравнение

(5)

Это
уравнение эллипса, оси которого по­вернуты
относительно координатных осей х
и у.
Ори­ентация эллипса
и его полуоси зависят довольно сложным
образом от амплитуд A
и В
и разности фаз α.

Попробуем найти
форму траектории для нескольких частных
случаев.

1.
Разность фаз α
равна нулю. В этом случае уравнение (5)
упрощается следующим образом:

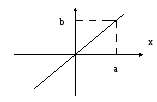
Отсюда получается
уравнение прямой:

Результирующее
движение является гармоническим
колебанием вдоль этой прямой с частотой
ω и ам­плитудой, равной

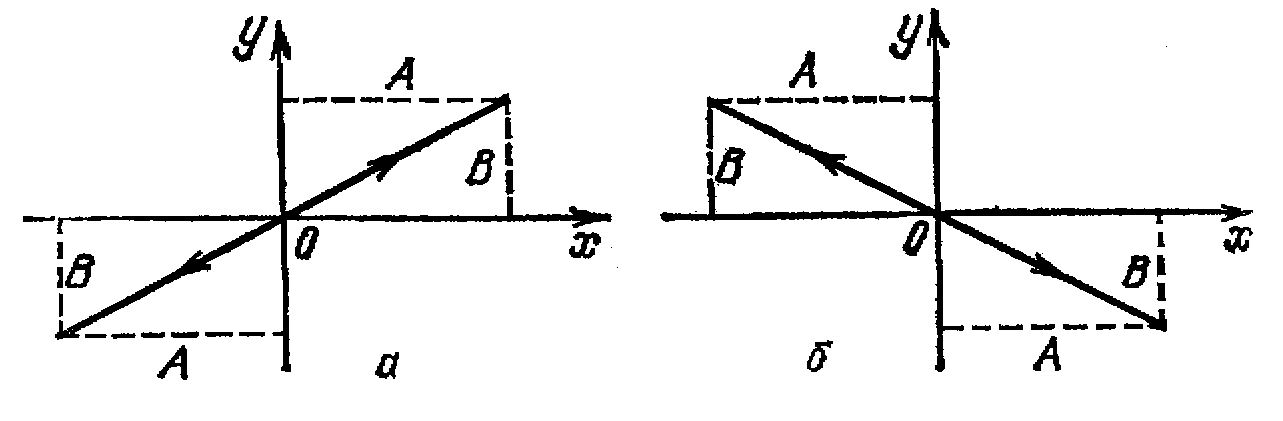
(рис. 1 а).

2.
Разность фаз α
равна ±π. Из уравнение (5)
имеет вид

Следовательно,
результирующее движение представ­ляет
собой гармоническое колебание вдоль
прямой

(рис. 1 б)

Рис.1

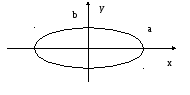
3. При

уравнение (5) переходит в уравнение
эллипса, приведенного к координатным
осям:

Полуоси
эллипса равны соответствующим амплиту­дам
колебаний. При равенстве амплитуд А
и В
эллипс превращается
в окружность.

Случаи

и

отличаются на­правлением
движения по эллипсу или окружности.

Следовательно,
равномерное движение по окружности
радиуса R
с угловой скоростью ω
может быть представлено как сумма двух
взаимно перпен­дикулярных колебаний:

,

(знак
плюс в выражении для у
соответствует движе­нию
против часовой стрелки, знак минус —
движе­нию по часовой стрелке).

Если
частоты взаимно перпендикулярных
колеба­ний не одинаковы, то траектории
результирующего движения имеют вид
сложных кривых, на­зываемых фигурами
Лиссажу.

Фигуры
Лиссажу

;

-параметрическая
запись кривой на плоскости

Рассмотрим
случаи

Равенство
частот и начальных фаз колебаний

1.

При
этих условиях запишем

Получим
взаимосвязь координат абсцисс и ординат
в виде

y

Равенство
частот и сдвиг по фазе на 90 градусов

2.

В
этом случае имеет место эллиптическая
взаимосвязь

(x/a)²
+ (y/b)²
= 1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  13.03.20163.54 Mб24Фелдман Л. Основы анализа поверхности.djvu

• #
• #
• #
• #
• #
• #
• #
• #

Сложение колебаний, теория и онлайн калькуляторы

Сложение колебаний

Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае
возникает необходимость выяснить, каким будет результирующее колебание.

Сложение колебаний направленных по одной прямой

Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:

[x_1=A_1{cos left({omega }_0t+{varphi }_1right) }left(1right),]

[x_2=A_2{cos left({omega }_0t+{varphi }_2right) }left(2right).]

Колебания (1) и (2) представим на векторной диаграмме в виде векторов ${overline{A}}_1$ и ${overline{A}}_2$ (рис.1).

Результирующее колебание отображает вектор $overline{A}$, который вращается с той же скоростью (${omega }_0$),
что векторы его составляющие. Сложением колебание векторов ${overline{A}}_1$+${overline{A}}_2$=$overline{A}$ является гармоническим колебанием:

[x=A{cos {(omega }_0t+varphi ) (3) }.]

Из рис.1 видно, что амплитуду результирующего колебания можно найти как:

[A=sqrt{A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }left(4right),}]

где $A_1$; $A_2$ — амплитуды сложенных колебаний; ${varphi }_2;;{varphi }_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:

[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}left(5right).]

Из выражения (4) видно, что если ${varphi }_2-{varphi }_1=0$, тогда получим колебание, амплитуда которого равна:

[A=A_1+A_2left(6right).]

При разности фаз равной ${varphi }_2-{varphi }_1=pm pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:

[A=left|A_1-A_2right|left(7right).]

Если частоты сложенных гармонических колебаний не равны, то есть векторы ${overline{A}}_1$и ${overline{A}}_2$ вращаются с разной скоростью, результирующее колебание гармоническим не будет. Вектор $overline{A}$ будет пульсировать по величине, и вращаться с переменной скоростью.

Суперпозиция взаимно перпендикулярных колебаний

Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой ${omega }_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:

[x=A_1{cos left({omega }_0t{+varphi }_1right) }left(8right),]

[y=A_2{cos left({omega }_0t+{varphi }_2right) }left(9right),]

Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:

Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${varphi }_2и{varphi }_1$:

[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}-frac{2xy}{A_1A_2}{cos left({varphi }_2-{varphi }_1right) }={sin}^2left({varphi }_2-{varphi }_1right)left(10right).]

Уравнение (10) — это уравнение эллипса.

В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:

[y=frac{A_2}{A_1}x или y=-frac{A_2}{A_1}x left(11right),]

что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:

[r=sqrt{x^2+y^2}.]

Если $Delta varphi ={varphi }_2-{varphi }_1=frac{pi }{2},$ уравнением траектории становится выражение:

[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}=1left(12right),]

что означает, траектория движения эллипс.

Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $Delta omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.

Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.

Примеры задач на сложение колебаний

Читать дальше: тело, брошенное горизонтально.

Сложением колебаний называют применение закона, описывающего состояние колебательной системы, если она принимает участие одномоментно в нескольких колебательных процессах.

При этом выделяют два предельных случая:

1. суммирование колебаний, имеющих одинаковые направления;
2. сложение взаимно нормальных колебаний.

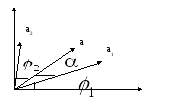
К первому варианту сложения колебаний можно отнести случай, когда груз ($a$) совершает колебания на пружине 1 относительно другого колеблющегося груза ($b$) и совместно с ним на пружине 2 (рис.1).

Такой случай реализуется при наложении колебаний скалярных физических параметров, характеризующих систему колебаний, например:

• давления;
• температуры;
• плотности;
• силы тока;
• заряда и т.д.

Суммирование однонаправленных гармонических колебаний

Сложение пары гармонических колебаний вида:

$s_1=A_1 sin (omega_1 t+varphi_1) (1)$ и $ s_2=A_2 sin (omega_2 t+varphi_2) (2)$

можно выполнить, если воспользоваться методом векторных диаграмм.

Рисунок 2 показывает векторы $vec A_1(t)$ и $vec A_2(t)$ амплитуд соответствующих колебаний в момент времени $t$. Фазы этих колебаний в обозначенный момент времени равны:

$Ф_1=omega_1 t+varphi_1 (3)$ и $Ф_2=omega_2 t+varphi_2 (4)$.

«Сложение гармонических колебаний» 👇

Суммарному колебанию $s=s_1+s_2$ соответствует вектор:

$A(t)=A_1(t)+A_2(t)$.

проекция вектора $s$ на ось $Y$ равна:

$s=A(t)sin(Ф(t))(5).$

Используя теорему косинусов, получим:

$A^2(t)=A_1^2+A_2^2+2A_1A_2cos (Ф_2(t)-Ф_1(t))(6),$

$tg ( Ф(t))=frac{A_1sin(Ф_1(t))+A_2sin(Ф_2(t))}{ A_1cos(Ф_1(t))+A_2cos(Ф_2(t))}(7).$

Когерентные и некогерентные гармонические колебания

Из выражения (8) следует, что гармонические колебания будут когерентными, если

• их круговые частоты будут одинаковыми:

  $omega_2=omega_1=omega.$

• в каждый момент времени разность фаз когерентных колебаний равна разности фаз их начальных колебаний:

  $ Ф_2(t)-Ф_1(t)=(varphi_2-varphi_2).$

Сложение двух гармонических однонаправленных когерентных колебаний дают колебание с той же круговой частотой $omega$, что исходные колебания, при этом имеем:

$s=s_1+s_2=Asin(omega t+varphi_0)(9),$

где $A^2=A_1^2+A_2^2+2A_1A_2cos (varphi_2-varphi_1)$;

$tg varphi_0=frac{A_1sin (varphi_1)+ A_2sin (varphi_2)}{ A_1cos (varphi_1)+ A_2cos (varphi_2)}$.

Амплитуда суммарных колебаний изменяется в зависимости от разности начальных фаз:

от $A=|A_1-A_2|$ при $varphi_2-varphi_1=pm (2n+1)pi$

до $A=A_1+A_2$ при $varphi_2-varphi_1=pm 2npi$,

где $n=0,1,2…$ — целое положительное число или ноль.

При $varphi_2-varphi_1=pm 2npi$ колебания происходят в одной фазе (колебания называют софазными).

Если $varphi_2-varphi_1=pm (2n+1)pi$ колебания происходя в противофазе.

Если складываются гармонические колебания с разными циклическими частотами (некогерентные колебания), получаются негармонические колебания. Векторы амплитуд $A_1$ и $A_2$ вращаются с разными угловыми скоростями, построенный на них параллелограмм постоянно искажается, его диагональ изменяет длину и совершает вращения с изменяющейся угловой скоростью.

Пару гармонических колебаний, имеющих разные круговые частоты можно приближенно считать когерентными только на малом отрезке времени, в течение которого разность фаз колебаний изменяется на малую величину.

Биения – это негармоническое колебание.

Суммирование взаимно перпендикулярных гармонических колебаний

Точка $N$ совершает одновременно два колебания. Они имеют одинаковые круговые частоты. Одно из них происходит вдоль оси $X$, другое вдоль оси $Y$. Их законы запишем как:

$x=A_1sin (omega t+varphi_1) (10)$ и

$y=A_2sin (omega t+varphi_2) (11),$

где $x$ и $y$ — декартовы координаты точки N.

Уравнение траектории движения точки N при этом:

$frac{x^2}{A_1^2}+frac{y^2}{A_2^2}-frac{2xy}{A_1A_2}cos (varphi_2-varphi_1)=sin^2 (varphi_2-varphi_1) (12)$.

Траектория движения точки имеет форму эллипса. Точка $M$ описывает данный эллипс за период суммируемых колебаний. Такие движения точки называют эллиптически поляризованными колебаниями.

Ориентация этого эллипса в плоскости $XOY$ и его размеры зависят от амплитуд складываемых колебаний $A_1$ и $A_2$ и разности начальных фаз $varphi_2-varphi_1$.

При $varphi_2-varphi_1=(2n+1)frac{pi}{2}$, где $n=0,pm 1, pm 2…$ оси эллипса будут совпадать с осями $OX$ и $OY$, при этом величины его полуосей равны $A_1$ и $A_2$:

$frac{x^2}{A_1^2}+frac{y^2}{A_2^2}(13).$

Если помимо прочего, $A_1=A_2$, то траекторией точки $N$ является окружность. При этом движение точки $N$ называют поляризованными циркулярно колебаниями (колебаниями которые поляризованы по кругу).

При $varphi_2-varphi_1=npi$ где $n=0,pm 1, pm 2…$, эллипс вырожден в отрезок прямой, при этом:

$y=pm (frac{A_2}{A_1})x (14),$

где знак плюс в выражении (14) при четных значениях $n$, то есть если складываются синфазные колебания; минус ставят при нечетных значения $n$, то есть если складываются колебания в противофазе. Такие колебания точки $N$ называют линейно поляризованными.

При линейно поляризованных колебаниях точка $N$ совершает гармонические колебания с частотой суммируемых колебаний и амплитудой, равной:

$A=sqrt{A_1^2+A_2^2}$

вдоль прямой линии, которая составляет с осью $OX$ угол:

$beta = arctg(frac{A_2}{A_1}cos (pi))(15).$

Пусть взаимно нормальные колебания, имеющие циклические частоты $pomega$ и $qomega$, где $p$ и $q$ — целые числа:

$x=A_1sin (pomega t+varphi_1)$ и $y=A_2sin (qomega t+varphi_2) (16).$

Координаты $x$ и $y$ точки $N$, которая совершает колебания, одновременно повторяется спустя одинаковые отрезки времени $T_0$, равные общему минимальному кратному:

$T_1=frac{2pi}{pomega}$ и $T_2=frac{2pi}{qomega}$ периодов вдоль осей $OX$ и $OY$. Следовательно, траекторией точки $N$ является замкнутая кривая. Форма этой кривой связана с соотношением между:

• амплитудами,
• частотами,
• начальными фазами

суммируемых колебаний. Эти траектории точки $N$, выполняющей гармонические колебания в двух взаимно нормальных плоскостях одновременно, называют фигурами Лиссажу.

Фигуры Лиссажу можно вписать в прямоугольник:

• с центром, совпадающим с началом координат;
• сторонами параллельными осям координат ($OX$ и $OY$) и находящимися по обе стороны от них на расстояниях равных $A_1$ $A_2$;
• отношение частот суммируемых колебаний определяет количество касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси $OY$ и со стороной, параллельной оси $OX$.