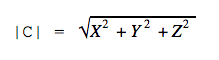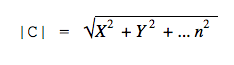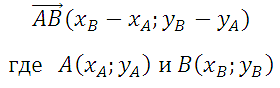Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
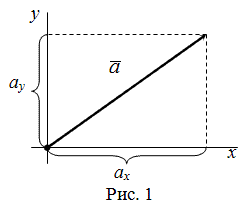
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ <1>; y_<1>right)$ находятся по формулам (рис. 4):
Направляющие косинусы
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Здесь $alpha$, $beta$ и $gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
Основное свойство направляющих косинусов
Сумма квадратов направляющих косинусов равна единице.
Операции над векторами в прямоугольной системе координат
Если задана плоскость O x y с векторами a → = a x , a y и b → = ( b x , b y ) , то мы можем разложить их по координатным векторам i → и j → . Тогда это будет иметь вид a → = a x · i → + a y · j → и b → = b x · i → + b y · j → . Чтобы найти сумму a → и b → и произведение a → на λ , рассмотрим:
a → + b → = a x · i → + a y · j → + b x · i → + b y · j → = ( a x + b x ) · i → + ( a y + b y ) · j →
λ · a → = λ · ( a x · i → + a y · j → ) = ( λ · a x ) · i → + ( λ · a y ) · j →
Это равенство справедливо по свойству операций над векторами.
Разложение векторов – это a → + b → и λ · a → , представленное в частях неравенства по i → и j → координатам. Координаты векторов a → + b → и λ · a → равны соответственно ( a x + b x , a y + b y ) и ( λ · a x , λ · a y ) .
Таким же образом a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) записываются как a → + b → = a x · i → + a y · j → + a z · k → + b x · i → + b y · j → + b z · k → = ( a x + b x ) · i ⇀ + ( a y + b y ) · j → + ( a z + b z ) · k → λ · a → = λ · ( a x · i → + a y · j → + a z · k → ) = ( λ · a x ) · i → + ( λ · a y ) · j → + ( λ · a z ) · k →
а значит a → + b → = ( a x + b x , a y + b y , a z + b z ) , λ · a → = ( λ · a x , λ · a y , λ · a z )
Отсюда делаем вывод, что координаты векторов a → и b → равны сумме соответствующих координат векторов a → и b → , координаты произведения вектора a → на λ приравниваются к соответствующим координатам вектора a → , умноженным на число в заданной системе координат.
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.
Нужно выполнить сложение a → = ( 2 , 3 — 1 3 ) и b → = ( — 1 , — 1 3 ) . Чему равны координаты произведения вектора a → на 3 .
Решение
Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a → + b → = ( 2 + ( — 1 ) , 3 — 1 3 + ( — 1 3 ) ) = ( 1 , — 1 3 ) .
Числовое значение умножается на каждую координату: 3 · a → = ( 3 · 2 , 3 · 3 — 1 3 ) = 2 3 , 3 — 3 3 .
Ответ: a → + b → = ( 1 , — 1 3 ) , 3 · a → = ( 2 3 , 3 — 3 3 )
Заданы векторы a → = ( 0 , 1 , — 2 ) , b → = ( — 1 , — 1 , 3 ) , c → = ( 4 , — 3 , 2 ) .
Каковы координаты вектора 2 · a → + 3 · ( b → — c → ) = 2 · a → + 3 · b → + ( — 3 ) · c → .
Решение
Применяя свойства векторов, получим: 2 · a → + 3 · ( b → — c → ) = 2 · a → + 3 · b → + ( — 3 ) · c → .
Подставляем значения координат и получаем: 2 · a → + 3 · b → + ( — 3 ) · c → = 2 · ( 0 , 1 , — 2 ) + 3 · ( — 1 , — 1 , 3 ) + ( — 3 ) · ( 4 , — 3 , 2 ) =
= ( 2 · 0 , 2 · 1 , 2 · ( — 2 ) ) + ( 3 · ( — 1 ) , 3 · ( — 1 ) , 3 · 3 ) + ( ( — 3 ) · 4 , ( — 3 ) · ( — 3 ) · 2 ) =
= ( 0 , 2 , — 4 ) + ( — 3 , — 3 , 9 ) + ( — 12 , 9 — 6 ) =
= ( 0 + ( — 3 ) + ( — 12 ) , 2 + ( — 3 ) + 9 , — 4 + 9 + ( — 6 ) ) = ( — 15 , 8 , — 1 )
Можно решить другим способом.
Обратим внимание на разложение a → , b → и c → :
a → = 0 · i → + 1 · j → + ( — 2 ) · k → = j → — 2 · k →
b → = ( — 1 ) · i → + ( — 1 ) · j → + 3 · k → = — i → — j → + 3 · k →
c → = 4 · i → + ( — 3 ) · j → + 2 · k → = 4 · i → — 3 · j → + 2 · k →
Исходя из свойств векторов, видим, что: 2 · a → + 3 · ( b → — c → ) = 2 · ( j → — 2 · k → ) + 3 · ( — i → — j → + 3 · k → — ( 4 · i → — 3 · j → + 2 · k → ) ) = = 2 · j → — 4 · k → + 3 · ( — 5 · i → + 2 · j → + 1 · k → ) = — 15 · i → + 8 · j → — k →
Значит, координаты вектора 2 · a → + 3 · ( b → — c → ) равны ( — 15 , 8 , — 1 ) .
Ответ: 2 · a → + 2 · ( b → — c → ) = ( — 15 , 8 , — 1 )
Вектор сумма координат точки б
Онлайн калькулятор. Сложение и вычитание двух векторов.
Этот онлайн калькулятор позволит вам очень просто найти сумму двух векторов или разность двух векторов для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание двух векторов и закрепить пройденый материал.
Калькулятор для сложения и вычитания двух векторов
Введите значения векторов.
Инструкция использования калькулятора для сложения и вычитания двух векторов
Ввод даных в калькулятор для сложения и вычитания двух векторов
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для сложения и вычитания двух векторов
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Сложение и вычитание двух векторов
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Вектор. Координаты вектора.
В прямоугольной системе координат х0у проекции х и у вектора на оси абсцисс и ординат называются координатами вектора. Координаты вектора общепринято указывать в виде (х, у), а сам вектор как:
=(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х1;у1) и B(x2;y2) можно вычислить:
= (x2 – x1 ; y2 – y1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х1;у1;z1) и B(x2;y2;z2) можно вычислить применив формулу:
= (x2 – x1 ; y2 – y1;z2 – z1).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора. (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты.
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат.
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов.
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Операции с векторами
Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
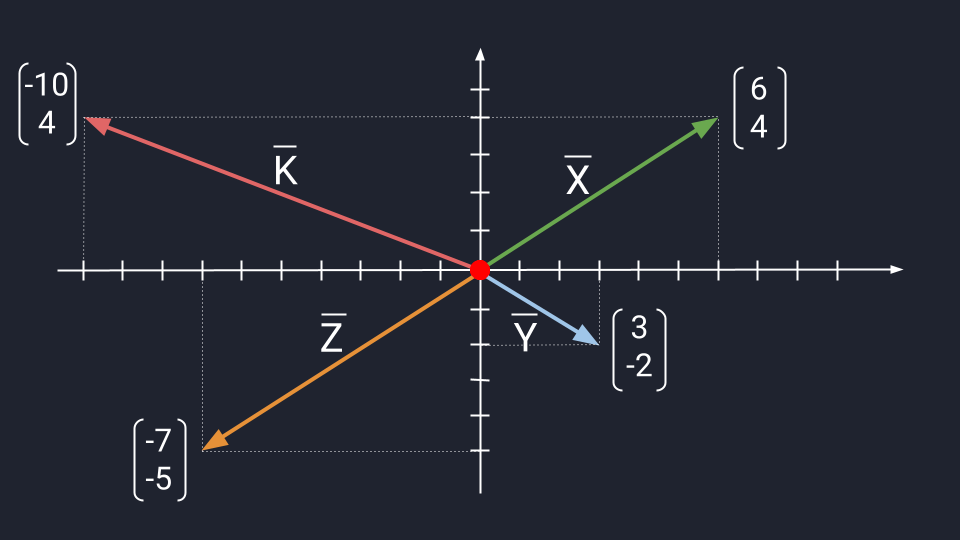
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
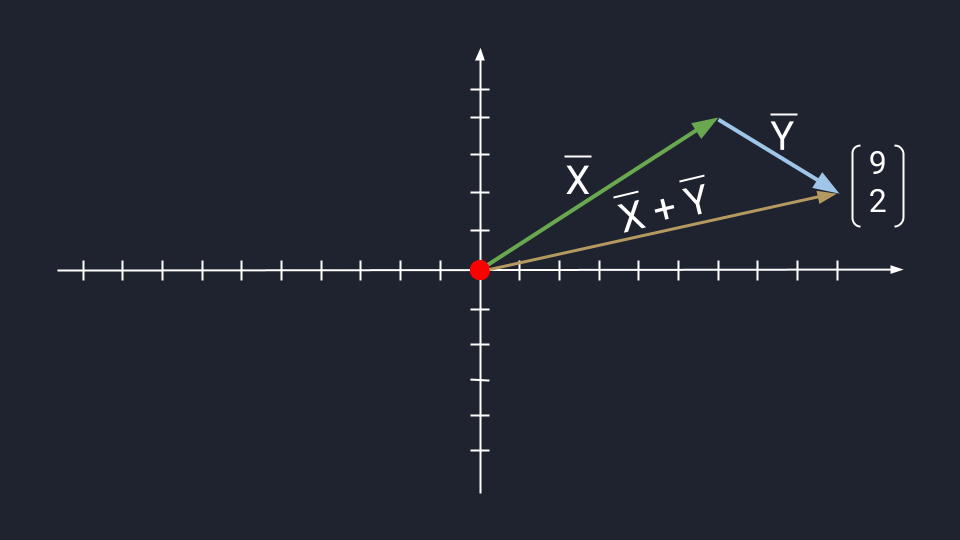
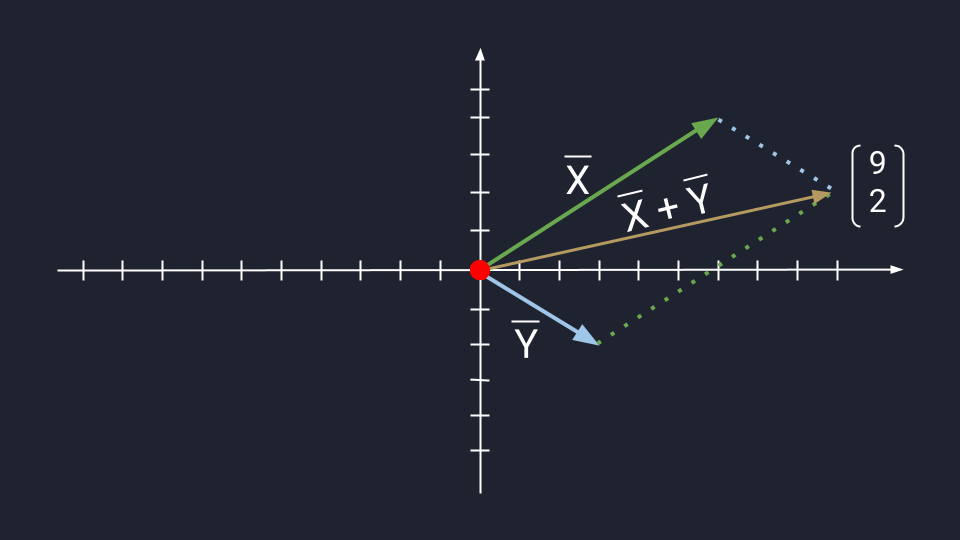
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Вычитание
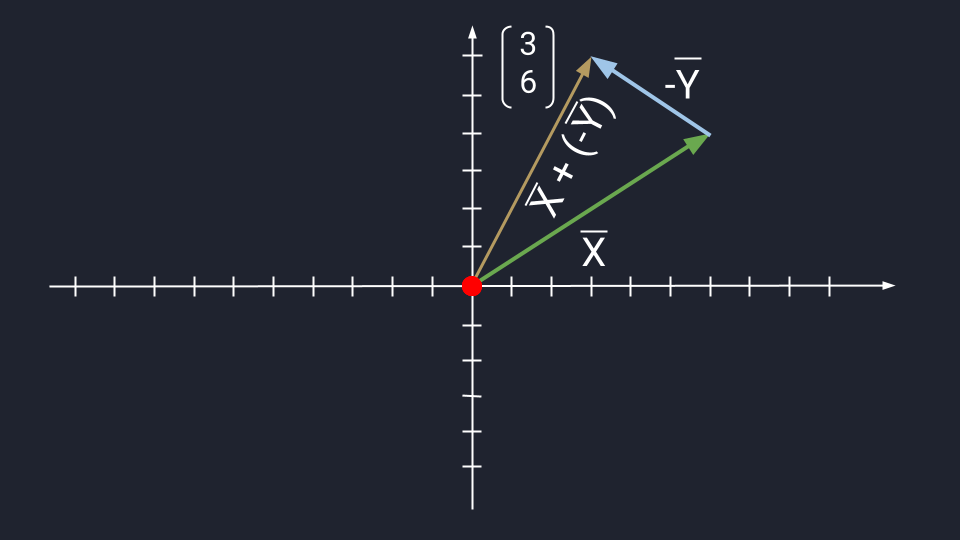
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
- У нас есть X = (6, 4) и Y = (3, −2).
- Превращаем формулу Х − Y в формулу Х + (−Y).
- Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
- Считаем: X + (−Y) = (3, 6).
Теперь посмотрим, как выглядит вычитание векторов на графике:
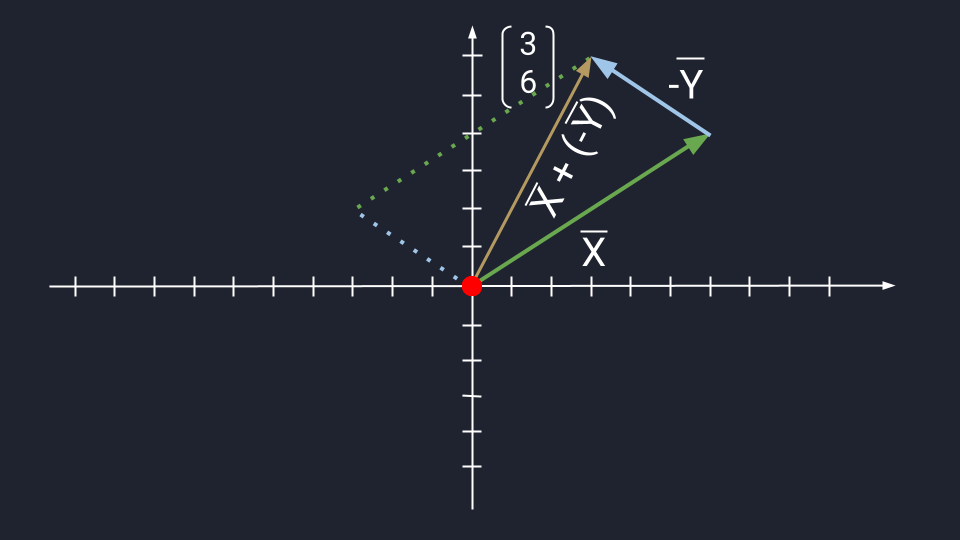
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 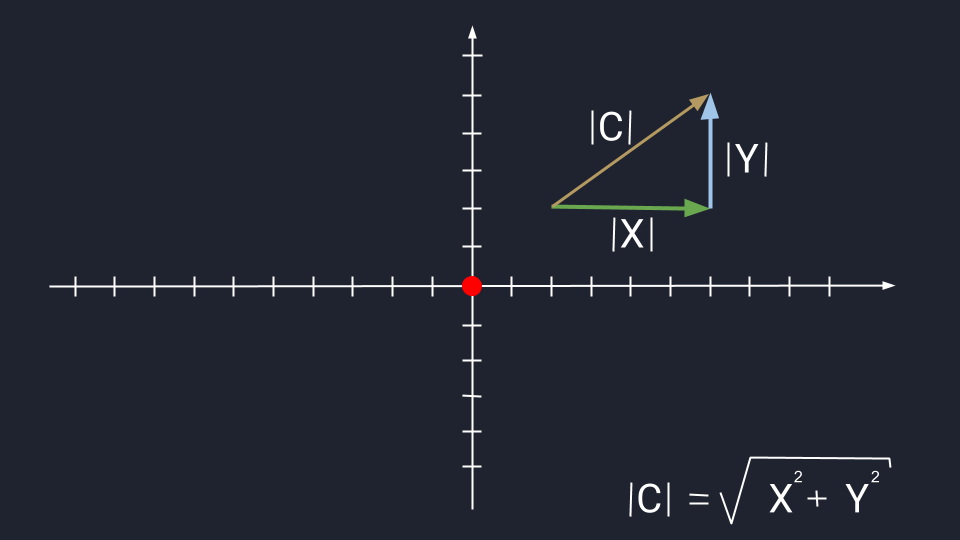
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Умножение и деление вектора на число
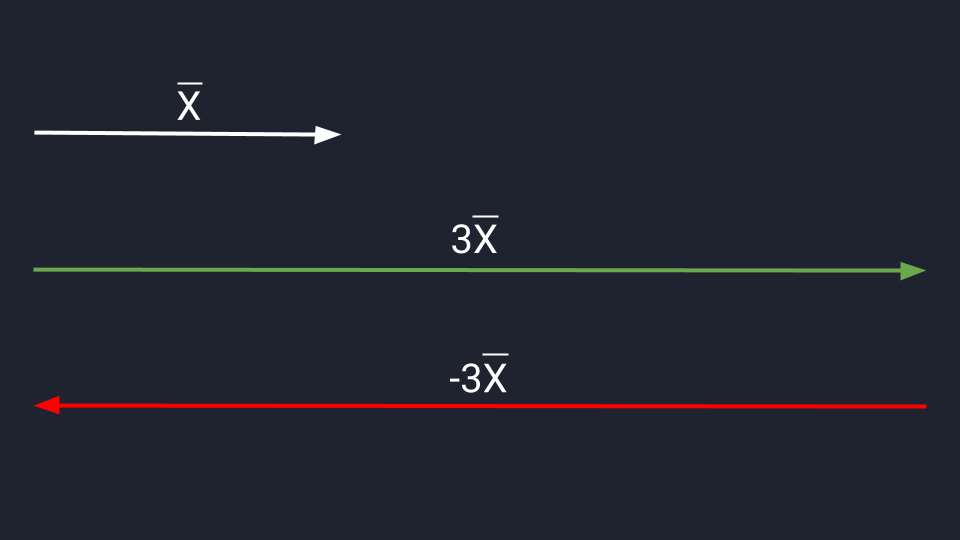
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
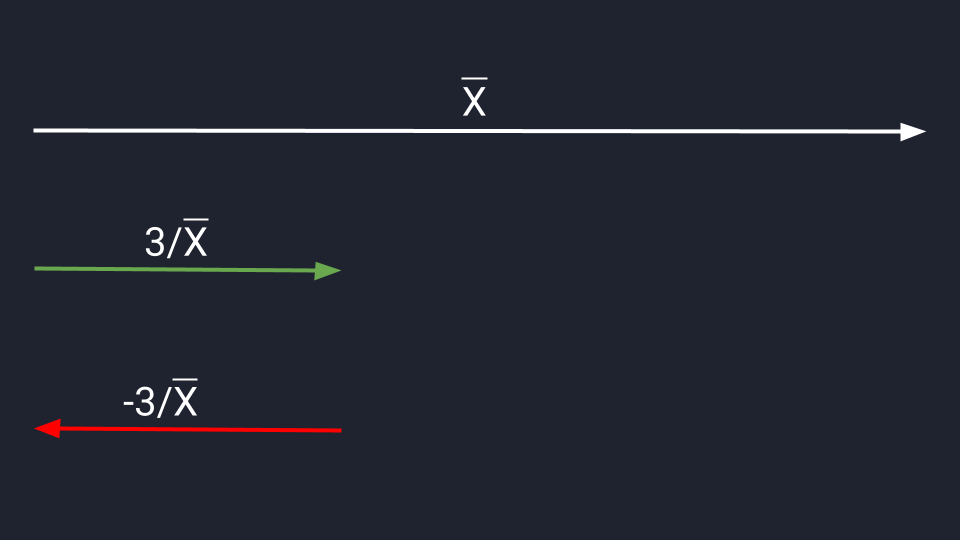
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
- векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
- если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
- а перемножение матриц — это и есть машинное обучение.
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Пример 1.
Найти сумму координат вектора, если даны координаты точек А(13; 17) и В(23; 27) – концов вектора.
Решение.
Найдем координат вектора АВ. Для этого от координаты его конца – точки В – вычтем координаты начала – точки А.
Координаты вектора АВ:
АВ=(23–13; 27–17)=(10; 10).
Найдем сумму его координат:
10+10=20.
Ответ. 20.
Пример 2.
Дан параллелограмм ABCD. Известны координаты двух его вершин А (14; –12; 14) и В (15; –11; –18), а точка О (17; –11; 14) – точка пересечения его диагоналей. Найти сумму координат вектора АD.
Решение.
Поскольку точкой пересечения диагонали параллелограмма делятся пополам, то ВО=OD. Таким образом, точка О – это середина отрезка BD.
Воспользуемся формулой для вычисления координат середины отрезка:
Подставим известные координаты:
Получили координаты точки D(19; –11; 46).
Найдем координаты вектора AD:
(19–14; –11–(–12); 46–14)=(5; 1; 32).
Сумма его координат равна:
5+1+32=38.
Ответ. 38.
Содержание:
- Координаты вектора
- Направляющие косинусы
- Сумма двух векторов, заданных координатами
- Умножение вектора на число
- Основное свойство направляющих косинусов
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении
и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).
Определение
Координатами вектора $overline{a}$ называются проекции
$a_{x}$ и $a_{y}$
данного вектора на оси $O x$ и
$O y$ соответственно:
$$a_{x}=Пр_{O x} bar{a}, a_{y}=Пр_{O y} bar{a}$$
Величина $a_{x}$ называется абсциссой вектора
$overline{a}$, а число $a_{y}$
— его ординатой. То, что вектор $overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $overline{a}=left(a_{x} ; a_{y}right)$.
Пример
Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
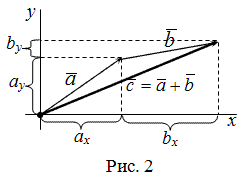
Пусть заданы $overline{a}=left(a_{x} ; a_{y}right)$ и $overline{b}=left(b_{x} ; b_{y}right)$,
тогда вектор $overline{c}=overline{a}+overline{b}$ имеет координаты
$left(a_{x}+b_{x} ; a_{y}+b_{y}right)$ (рис. 2).
Определение
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$
Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
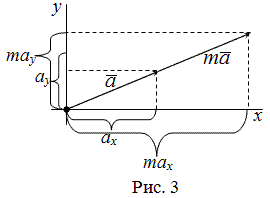
Умножение вектора на число
Если задан $overline{a}=left(a_{x} ; a_{y}right)$, то тогда вектор
$m overline{a}$ имеет координаты
$m overline{a}=left(m a_{x} ; m a_{y}right)$, здесь
$m$ — некоторое число (рис. 3).
Определение
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное
число.
Пример
Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$
Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$
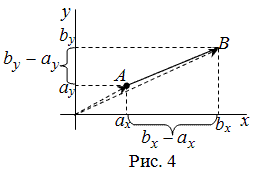
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $Aleft(a_{x} ; a_{y}right)$ и $Bleft(b_{x} ; b_{y}right)$.
Тогда координаты вектора $overline{A B}=left(x_{1} ; y_{1}right)$ находятся по формулам (рис. 4):
$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$
Определение
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат
конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Определение
Направляющими косинусами вектора называются косинусы углов, образованных вектором с
положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.
Если в пространстве задан вектор $overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то
его направляющие косинусы вычисляются по формулам:
$cos alpha=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos beta=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos gamma=frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$
Здесь $alpha$, $beta$ и
$gamma$ — углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.
Основное свойство направляющих косинусов
Определение
Сумма квадратов направляющих косинусов равна единице.
1
$cos ^{2} alpha+cos ^{2} beta+cos ^{2} gamma=1$
Если известны направляющие косинусы вектора $overline{a}=left(a_{x} ; a_{y}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta$
Аналогичные формулы имеют место и в трехмерном случае — если известны направляющие косинусы вектора
$overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta, a_{z}=|overline{a}| cos gamma$
Читать дальше: длина (модуль) вектора.
Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:
Формула для определения длины вектора, если известны координаты его начала и конца:
Формула для определения длины вектора, если известны его координаты:
27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.
Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:
Координаты вектора нам даны, координаты его начала тоже, значит:
Следовательно можем найти координаты точки В:
х2 – 2 = 6 у2 – 4 = 2
х2 = 8 у2 = 6
Таким образом, ордината точки В равна 6.
Ответ: 6
27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B.
Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:
Координаты вектора и координаты его начала даны, значит:
Можем найти координаты точки В:
х2 – 3 = 9 у2 – 6 = 3
х2 = 12 у2 = 9
Таким образом, сумма координат точки В равна 21.
Ответ: 21
27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат.
Нам известны координаты вектора и координаты его конца, значит:
Можем найти координаты точки А:
5 – х1 = 3 3 – у1 = 1
х1 = 2 у1 = 2
Таким образом, абсцисса точки А равна двум, ордината тоже равна двум, а сумма координат равна 2+2 = 4.
Ответ: 4
27731 Найдите квадрат длинны вектора a+b.
В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:
Или в другой форме:
Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов.
Рассмотрим вектор:
Рассмотрим вектор:
*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.
Теперь найдём координаты вектора являющегося их суммой:
(2 + 8; 6 + 4) = (10;10)
Таким образом, длина вектора являющегося суммой векторов a и b равна:
Следовательно квадрат длины будет равен 200.
*Имея опыт в решении подобных задач, можно сразу записывать:
Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.
Ответ: 200
27733. Найдите квадрат длины вектора a – b.
Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.
Координаты данных векторов нам уже известны (из предыдущей задачи):
Теперь найдём координаты вектора, который является их разностью:
(2 – 8; 6 – 4) = (–6;2)
Таким образом, длина вектора, который является разностью векторов
Следовательно квадрат её длины будет равен 40.
*Можно сразу записывать и вычислять:
Ответ: 40
27723. Найдите сумму координат вектора АВ.
Посмотреть решение
27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.
Посмотреть решение
27730. Найдите сумму координат вектора а + b.
Посмотреть решение
27732. Найдите сумму координат вектора а–b.
Посмотреть решение
27736. Найдите сумму координат вектора а + b
Посмотреть решение
27739. Найдите квадрат длины вектора а–b.
Посмотреть решение
Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!
На этом всё. Если что-то непонятно, пишите. Успеха Вам!
С уважением, Александр Крутицких
Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!..
P.S: Делитесь этой статьёй в сетях.
Сначала вопрос вызвал недоумение. Ведь сумма двух координат не имеет никакого практического значения. Немного напоминает задачку про складывание яблок со сливами, чтобы узнать количество вишен, но и в ней можно получить корзинку фруктов.
А потом попалась задача, в которой напрямую просили сложить координаты:
И вот её решение:
И таких задач со странным заданием множество.
Теперь стало понятно, откуда ноги растут. Просто в качестве ответа необходимо было предоставить одну единственную цифру, не вдаваясь в корректность постановки вопроса.
Вопрос в другом, что будет с молодыми неокрепшими головами после решения задач, от которых у взрослых крыша едет.