Как найти сумму кординат векторов - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Координаты вектора
Направляющие косинусы
Сумма двух векторов, заданных координатами
Умножение вектора на число
Основное свойство направляющих косинусов

Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении
и длине.

Координаты вектора

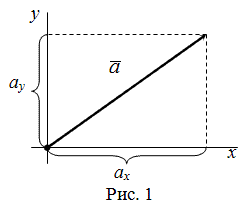
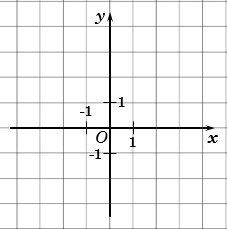
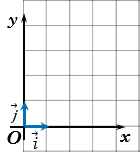
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).

Определение

Координатами вектора $overline{a}$ называются проекции
$a_{x}$ и $a_{y}$
данного вектора на оси $O x$ и
$O y$ соответственно:

$$a_{x}=Пр_{O x} bar{a}, a_{y}=Пр_{O y} bar{a}$$

Величина $a_{x}$ называется абсциссой вектора
$overline{a}$, а число $a_{y}$
— его ординатой. То, что вектор $overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $overline{a}=left(a_{x} ; a_{y}right)$.

Пример

Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.

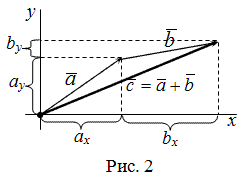
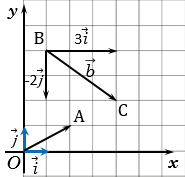
Сумма двух векторов, заданных координатами

Пусть заданы $overline{a}=left(a_{x} ; a_{y}right)$ и $overline{b}=left(b_{x} ; b_{y}right)$,
тогда вектор $overline{c}=overline{a}+overline{b}$ имеет координаты
$left(a_{x}+b_{x} ; a_{y}+b_{y}right)$ (рис. 2).

Определение

Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$

Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$

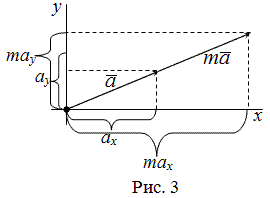
Умножение вектора на число

Если задан $overline{a}=left(a_{x} ; a_{y}right)$, то тогда вектор
$m overline{a}$ имеет координаты
$m overline{a}=left(m a_{x} ; m a_{y}right)$, здесь
$m$ — некоторое число (рис. 3).

Определение

Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное
число.

Пример

Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$

Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$

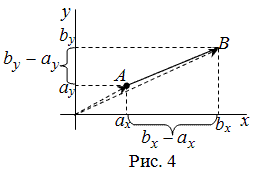
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $Aleft(a_{x} ; a_{y}right)$ и $Bleft(b_{x} ; b_{y}right)$.
Тогда координаты вектора $overline{A B}=left(x_{1} ; y_{1}right)$ находятся по формулам (рис. 4):

$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$

Определение

Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат
конца отнять соответствующие координаты начала.

Пример

Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$

Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$

Направляющие косинусы

Определение

Направляющими косинусами вектора называются косинусы углов, образованных вектором с
положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.

Если в пространстве задан вектор $overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то
его направляющие косинусы вычисляются по формулам:

$cos alpha=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos beta=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos gamma=frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$

Здесь $alpha$, $beta$ и
$gamma$ — углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.

Основное свойство направляющих косинусов

Определение

Сумма квадратов направляющих косинусов равна единице.

$cos ^{2} alpha+cos ^{2} beta+cos ^{2} gamma=1$

Если известны направляющие косинусы вектора $overline{a}=left(a_{x} ; a_{y}right)$,
то его координаты могут быть найдены по формулам:

$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta$

Аналогичные формулы имеют место и в трехмерном случае — если известны направляющие косинусы вектора
$overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$,
то его координаты могут быть найдены по формулам:

$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta, a_{z}=|overline{a}| cos gamma$

Читать дальше: длина (модуль) вектора.

Источник

Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).

Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.

Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ <1>; y_<1>right)$ находятся по формулам (рис. 4):

Направляющие косинусы

Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.

Здесь $alpha$, $beta$ и $gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.

Основное свойство направляющих косинусов

Сумма квадратов направляющих косинусов равна единице.

Онлайн калькулятор. Сложение и вычитание двух векторов.

Этот онлайн калькулятор позволит вам очень просто найти сумму двух векторов или разность двух векторов для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание двух векторов и закрепить пройденый материал.

Калькулятор для сложения и вычитания двух векторов

Введите значения векторов.

Инструкция использования калькулятора для сложения и вычитания двух векторов

Ввод даных в калькулятор для сложения и вычитания двух векторов

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для сложения и вычитания двух векторов

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Теория. Сложение и вычитание двух векторов

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач	a + b = x + b_x; a_y + b_y>
Для трехмерных задач	a + b = x + b_x; a_y + b_y; a_z + b_z>
Для n-мерных векторов	a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

Для плоских задач	a — b = x — b_x; a_y — b_y>
Для трехмерных задач	a — b = x — b_x; a_y — b_y; a_z — b_z>
Для n-мерных векторов	a — b = 1 — b₁; a₂ — b₂; . a_n — b_n>

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

источники:

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Сложение векторов

Формула

Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$

Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:

$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$

При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.

Примеры решений

Пример

Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора.

Решение

Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй:

$$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$

В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a}+overline{b} = (3;7) $$

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Метод координат
Координаты вектора

Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.

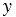
На рисунке выше оси и перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.

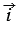
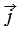
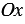
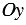
Отложим от начала координат О единичные векторы и так, чтобы их направления совпадали с направлениями осей и соответственно.

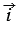
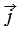
Векторы и называют координатными векторами.

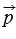
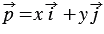
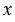
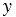
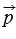
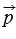
Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде , причем коэффициенты разложения и определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.

Координаты вектора записывают в фигурных скобках после обозначения вектора: .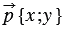

На рисунке выше .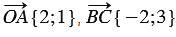

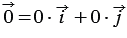
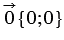
Нулевой вектор можно представить в виде , следовательно, его координаты равны нулю: .

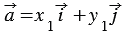
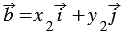
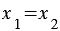
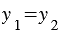
Если векторы и равны, то и . Значит, координаты равных векторов соответственно равны.

Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:

1⁰. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.

Доказательство

Дано: , , .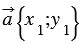

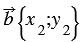
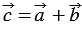
Доказать: .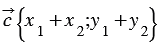

Доказательство:

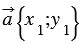
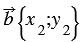
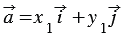
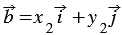
По условию и , тогда и .

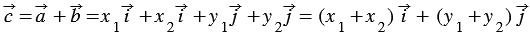
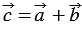
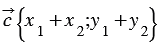
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.

2⁰. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Доказательство

Дано: , , .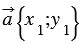

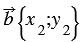
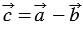
Доказать: .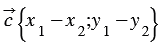

Доказательство:

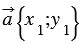
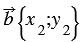
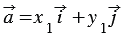
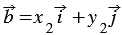
По условию и , тогда (1) и . (2)

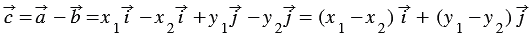
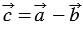
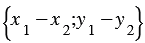
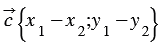
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.

3⁰. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Доказательство

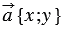
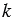
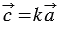
Дано: , — число, .

Доказать: .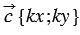

Доказательство:

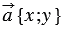
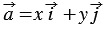
По условию , значит, .

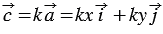
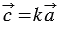
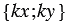
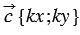
Умножим последнее равенство на число и используя свойства умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.

Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

Пример

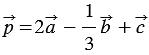
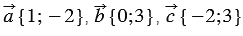
Найти координаты вектора , если известно, что .

Решение:

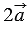
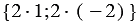
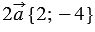
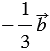
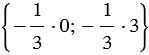
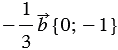
По правилу 3⁰ вектор будет иметь координаты , т.е. , вектор координаты , т.е. .

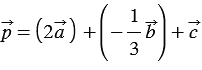
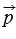
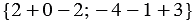
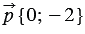
Так как , то координаты вектора можно найти по правилу 1⁰: , т.е. .

Ответ: .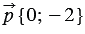

Советуем посмотреть:

Разложение вектора по двум неколлинеарным векторам

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Метод координат

Правило встречается в следующих упражнениях:

7 класс

Задание 917,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 935,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 943,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 949,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 22,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1007,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 21,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

При подготовке к ЕГЭ по математике, ученикам обязательно нужно повторить, как найти сумму координат вектора.

Дело в том, что нередко ученики путают понятия суммы координат вектора и суммы координат двух векторов. А на экзамене эта путаница проявляется в неумении решить простую задачу по нахождению суммы координат. Между тем ничего сложного в это задаче нет. Нужно, прежде всего, определить сами координаты вектора, а потом уже находить их сумму.

Наглядно посмотреть на примере, как это делается, можно по этой ссылке.

Источник