Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
8.2.4. Применение теоремы Виета
Часто требуется найти сумму квадратов (x1 2 +x2 2 ) или сумму кубов (x1 3 +x2 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:
Помочь в этом может теорема Виета:
Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Выразим через p и q:
1) сумму квадратов корней уравнения x 2 +px+q=0;
2) сумму кубов корней уравнения x 2 +px+q=0.
Решение.
1) Выражение x1 2 +x2 2 получится, если взвести в квадрат обе части равенства x1+x2=-p;
(x1+x2) 2 =(-p) 2 ; раскрываем скобки: x1 2 +2x1x2+ x2 2 =p 2 ; выражаем искомую сумму: x1 2 +x2 2 =p 2 -2x1x2=p 2 -2q. Мы получили полезное равенство: x1 2 +x2 2 =p 2 -2q.
2) Выражение x1 3 +x2 3 представим по формуле суммы кубов в виде:
Еще одно полезное равенство: x1 3 +x2 3 =-p·(p 2 -3q).
Примеры.
3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x1 2 +x2 2 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения
x1+x2=-p=3, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 1) равенство:
x1 2 +x2 2 =p 2 -2q. У нас -p=x1+x2=3 → p 2 =3 2 =9; q=x1x2=-4. Тогда x1 2 +x2 2 =9-2·(-4)=9+8=17.
4) x 2 -2x-4=0. Вычислить: x1 3 +x2 3 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения x1+x2=-p=2, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 2) равенство: x1 3 +x2 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.
Ответ: x1 3 +x2 3 =32.
Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.
5) 2x 2 -5x-7=0. Не решая, вычислить: x1 2 +x2 2 .
Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.
По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.
Решаем так же, как пример 3), используя равенство: x1 2 +x2 2 =p 2 -2q.
x1 2 +x2 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.
Ответ: x1 2 +x2 2 =13,25.
6) x 2 -5x-2=0. Найти:
Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x1 2 +x2 2 =p 2 -2q.
В нашем примере x1+x2=-p=5; x1∙x2=q=-2. Подставляем эти значения в полученную формулу:
7) x 2 -13x+36=0. Найти:
Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
У нас x1+x2=-p=13; x1∙x2=q=36. Подставляем эти значения в выведенную формулу:
Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax 3 + bx 2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b 2 /3a 2 + c/a
- q= 2b 3 /27a 3 — bc/3a 2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q 3 + ax 2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- ch(x)=(e x +e -x )/2
- Arch(x) = ln(x + (x 2 -1) 1/2 )
- sh(x)=(e x -e -x )/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
Консультации и техническая
поддержка сайта: Zavarka Team
http://mathematics-repetition.com/8-2-4-primenenie-teorem-vieta/
http://dpva.ru/Guide/GuideMathematics/Equations/cubeEquationsUniversalMethods/
Итак,
мы
показали в п. 4, что достаточным условием
приводимости многочлена над полями С,
R,
Q
является наличие хотя бы одного корня
многочлена f(x)
в поле С, R
или Q.
Дня отыскания этих корней приходится
решать уравнения n
— ой степени в поле С, R
или Q.
Мы уже отмечали, что если
многочлен
f(x)
имеет рациональный корень, то он приводим
и над полем R,
и над С. Поэтому, обычно, решение задачи
о приводимости многочлена начинается
с поиска его рациональных корней.
Необходимые, но не достаточные условия
существования рациональных корней
многочлена с целыми коэффициентами
даёт следующая теорема.
Теорема
1.
Если
—
рациональный корень многочленаf(x)
с целыми коэффициентами, причем (p,
q)
= l,
то числитель дроби (р) является делителем
свободного члена а0,
а знаменатель (q)
является делителем старшего коэффициента
аn.
Доказательство.
Пусть
—
корень многочленаf(x)=anxn
+
an-1xn-1
+…+
a1x
+ a0,
где все аi
Î
Z.
Подставим
,
где (p,
q)
= l,
q
¹
1 в многочлен, получим:
(1)
Умножим
обе части равенства (1) на qn,
тогда:
anpn
+
an-1qpn-1
+…+
a1
pqn-1
+
a0qn
= 0 (2)
Из равенства (2)
сначала можно выразить
anpn
= (-an-1pn-1
-…- a1pqn-2
—
a0qn-1)q
=> (аn
/q),
а
потом
-a0qn
=
p(anpn-1
+
an-1pn-2q+…
…+ а1qn-l)
=> (а0
/p) т.к.
(p, q) = 1
Замечание
1.
Так как
Z,
0 имеет лишь конечное число делителей,
то теорема позволяет, путем конечного
числа шагов, найти все рациональные
числа многочлена или проверить что их
нет.
Следствие
1.
Нормированный многочлен f
(x)
Z[x]
не имеет дробных корней;
Следствие
2.
Целый корень многочлена f(x)Z[x]
является
делителем свободного члена.
Задача
1.
Разложить многочлен
f(x)
= x6
— 2х5
+ х4
+ 6х3
— 10х2
— 4х + 8
над
полями Q,
R
и С.
Решение.
На
основании теоремы (1), рациональные корни
данного многочлена следует искать среди
делителей числа 8, т.к. аn
=
1
Делители:
+ 1, ±2,
±4,
±8.
Известно,
что число ()
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
— )
(Смотри п. 4). Следовательно, для проверки,
какие из чисел ±1, ±2, ±4, ±8 являются
рациональными корнями, можно использовать
схему Горнера, а можно непосредственно
проверить, будет ли f(±1)
= 0, f(±2)
= 0,
f(±4)
= 0, f(±8)
= 0.
|
1 |
-2 |
1 |
6 |
-10 |
-4 |
8 |
|
|
1 |
1 |
-1 |
0 |
6 |
-4 |
-8 |
0 |
|
1 |
1 |
0 |
0 |
6 |
2 |
-6 |
|
|
-1 |
1 |
-2 |
2 |
4 |
-8 |
0 |
|
|
-1 |
1 |
-3 |
5 |
-1 |
-7 |
||
|
2 |
1 |
0 |
2 |
8 |
8 |
||
|
-2 |
1 |
-4 |
10 |
-16 |
24 |
||
|
4 |
1 |
2 |
10 |
44 |
166 |
||
|
-4 |
1 |
-6 |
26 |
… |
0 |
||
|
8 |
1 |
6 |
50 |
… |
0 |
||
|
-8 |
1 |
-10 |
42 |
… |
- |
Итак,
f(x)
= (x
— l)(x
+ l)(
x4
—
2x3
+
2x2
+
4x
— 
Чтобы
найти разложение над полями R
и С, нужно найти действительные и
комплексные корни этого многочлена,
для этого надо решить уравнение четвертой
степени х4
—
2х3
+
2х2
+
4х — 8 = 0.
Для
решения уравнений 4-ой степени разработан
частный метод
Феррари.
1-й шаг. Оставляем
в левой части равенства члены 4-ой и 3-ей
степени, остальные переносим в правую
часть, получим:
х4
—
2х3
=
-2х2
—
4х + 8
2-й
шаг. Дополняем левую часть равенства
до полного квадрата: х4
—
2х3
+
х2
=
х2
—
2х2
—
4х + 8
(х2
—
х)2
=
-х2
—
4х + 8
3-й шаг. Вводим
новую переменную (у) и дополняем левую
часть еще раз до полного квадрата,
получим:
(х2
—
х)2+2(х2—
x)у
+ у2
=
-х2
—
4х + 8 + 2(х2
—
х)у +
y2
[(x2-x)+y)]2
= (2y-1)x2+(-2y-4)x+(y2+8)
*
4-й
шаг. Потребуем, чтобы правая часть
также стала полным
квадратом,
для этого D
= В2
— 4АС = О
D=(-2y
— 4)2
—
4(2y
— l)(y2
+

у3
—
у2
+
6у – 6 = 0
Это
уравнение имеет рациональный корень
у0
=
1.
5-й
шаг. Подставим у0
в правую
и
левую части уравнения (*) вместо у.
Получим: (х2-х+1)2
= х2-6х+9
= (х-3)2
x3
=
-2,
x4
=
2
Итак,
многочлен f(x)
над полем С может быть представлен в
виде: f(х)
= (х — 1)(х + 1)(х + 2)(х
— 2)(x
— 1- i3)(x
— 1 + i3)
Для
того, чтобы найти разложение многочлена
над полем R,
нужно перемножить две последние скобки,
тогда:
f(х)
= (х — 1)(х + 1)(х + 2)(x
—
2)((х
— 1)2
+ 3).
Задача
2.
Разложить многочлен f(x)
= х4
— 2х3
— 6х2
— 4х — 1
Решение.
Так как многочлен
4-ой степени, то можно методом Феррари
сразу искать его действительные и
комплексные корни, а можно как и в первом
случае, найти сначала рациональные
корни (если они есть).
Так
как аn
= 1, то многочлен может иметь в качестве
рациональных корней целые числа, которые
являются делителями свободного члена
а0
= 1, т.е. ±1. Непосредственной подстановкой
убеждаемся, что (-1) является корнем, а
(1) нет, т.к. f(-l)
= 0, f(l)
¹
0.
Тогда,
f(x)
= (х + 1)( х3
— 3х2
— 3х — 1) над полем Q.
Теперь
найдем корни многочлена в поле С и R.
Для этого решим
уравнение:
х3
— 3х2
— 3х — 1 = 0.
Это
уравнение 3-ей степени, для таких уравнений
также существует частный метод решения
— метод
Кардано.
1-
й шаг. Приведем уравнение к виду, не
содержащему второй степени неизвестного.
Для этого введем подстановку
где (а) коэффициент при х2
.
Тогда,
(у + 1)3
— 3(у + 1)2
— 3(у + 1) – 1 = 0. Раскрыв скобки и приведя
подобные, получим: у3
— 6у — 6 = 0.
2-й
шаг. Полагаем, что у
=
+ ,
где
,
р — коэффициент при у,q
— свободный член.
В
нашем случае р = -6, q
= -6 Поэтому
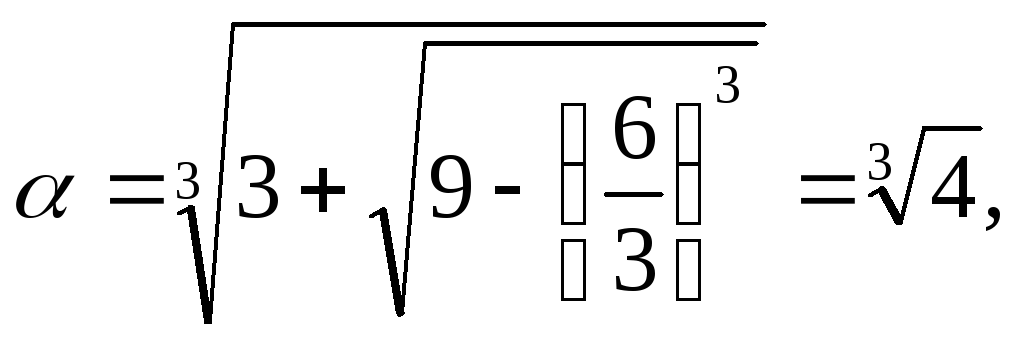
.
Тогда,
,
Наконец, находим
(х) из формулы х = у + 1
,
Тогда,
f(x)
= (x
+ l)(x
– x1)(x
— x2)(x
— x3)
— разложение многочлена над полем С.
Для
нахождения разложения многочлена f(x)
над полем действительных чисел R
достаточно в полученном выше разложении
перемножить скобки, соответствующие
сопряженным комплексным корням.
Тогда:
над полемR.
Замечание
2.
Если дан многочлен f(х),
степень которого выше четвертой, причем
он не имеет рациональных корней, то
задача разложения многочлена f(x)
на неприводимые многочлены над полем
С и R
становится трудноразрешимой, т.к. общих
методов решения уравнений n-ой
степени, где n
> 4 не существует.
Существуют
различные методы приближенного вычисления
действительных корней многочлена f(x)
(метод хорд, метод касательных и т.п.)
Замечание
3.
В том случае, когда нужно найти сумму
корней многочлена f(x),
могут быть использованы формулы Виета,
которые устанавливают зависимость
между корнями и коэффициентами многочлена.
Выведем эти формулы:
Пусть
f(z)
= zn
+
c1zn-1
+
c2zn-2
+…+ cn-1z
+ cn
и 1,
2,…,
n
корни
этого многочлена в поле С, тогда
zn
+
c1zn-1
+
c2zn-2
+… + cn-1z
+ cn
= (z
— a1)(z
— a2)…(z
— an)
= = zn
– (a1
+ a2
+…+
an)zn-1
+ (a1a2
+ a1a3
+…+
an-1an)zn-2
+…+
+(-1)n
(a1a2
…an)
Приравняв
коэффициенты при соответствующих
степенях, получим формулы Виета:
с1
=
-(a1
+ a2
+…+ an)
с2
= (a1a2
+ a1a3
+…+
an-1an)
c3
= -(a1a2a3+
a1a2a4
+…+ an-2an-1an)
сn
=
(-1)n
(a1a2
…an)
Задача
3.
Найти сумму кубов корней многочлена
f(x)
= x4
+ 2х3
+ х2
+ 5х + 3, f(x)Q[x]
Решение.
Над
полем комплексных чисел С многочлен
f(x)
имеет четыре корня: х1,
х2,
х3,
х4.
Нам нужно найти X13+
X23+
X33+
X43
не находя самих корней.
По формулам Виета
х1+x2+
х3+
х4
= -2 =1
х1х2
+
х1х3
+
х1х4
+
x2x3+
х2х4
+
х3х4
=
1 = 2
х1х2х3
+ x1x2x4
+ х1х3х4
+
х2х3х4
= -5 = s3
х1х2х3х4
= 3 = s4
Тогда
X13+
X23+
X33+
X43
= 13
—
312
+ 33
=
=(-2)3
— 3(-2)l
+ 3(-5) = -17
Ответ: -17.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Формулы сокращенного умножения
- Сумма и разность кубов двух выражений
Сумма кубов двух выражений
Найдем произведение двучлена 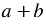
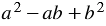
Итак, мы получили тождество:
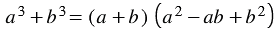
Многочлен 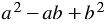
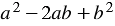
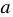
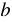
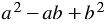
Правило:
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Пример:
Разложите на множители многочлен 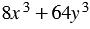
Решение:
Используя свойства степени, представляем данный многочлен в виде суммы кубов двух выражений, получаем:
Разность кубов двух выражений
Найдем произведение двучлена 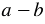
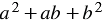
Итак, мы получили тождество:
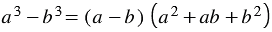
Многочлен 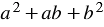
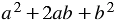
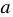
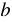
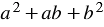
Правило:
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Пример:
Разложите на множители многочлен 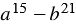
Решение:
Используя свойства степени, представляем данный многочлен в виде разности кубов двух выражений, получаем:
Советуем посмотреть:
Произведение разности и суммы двух выражений. Разность квадратов двух выражений.
Квадрат суммы и квадрат разности двух выражений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 675,
Мерзляк, Полонский, Якир, Учебник
Номер 676,
Мерзляк, Полонский, Якир, Учебник
Номер 677,
Мерзляк, Полонский, Якир, Учебник
Номер 686,
Мерзляк, Полонский, Якир, Учебник
Номер 697,
Мерзляк, Полонский, Якир, Учебник
Номер 699,
Мерзляк, Полонский, Якир, Учебник
Номер 714,
Мерзляк, Полонский, Якир, Учебник
Номер 730,
Мерзляк, Полонский, Якир, Учебник
Номер 739,
Мерзляк, Полонский, Якир, Учебник
Номер 1054,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 23,
Мерзляк, Полонский, Якир, Учебник
Номер 24,
Мерзляк, Полонский, Якир, Учебник
Номер 25,
Мерзляк, Полонский, Якир, Учебник
Номер 121,
Мерзляк, Полонский, Якир, Учебник
Номер 122,
Мерзляк, Полонский, Якир, Учебник
Номер 123,
Мерзляк, Полонский, Якир, Учебник
Номер 158,
Мерзляк, Полонский, Якир, Учебник
Номер 189,
Мерзляк, Полонский, Якир, Учебник
Номер 218,
Мерзляк, Полонский, Якир, Учебник
Номер 520,
Мерзляк, Полонский, Якир, Учебник
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители:
вынесение общего множителя за скобки
и
способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители
с применением формул сокращённого умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все
формулы сокращённого умножения себе на небольшую
шпаргалку.
Вспомним, как выглядит формула суммы кубов.
a3 + b3 =
(a + b)(a2 − ab + b2)
Формула суммы кубов не очень проста для запоминания, поэтому рекомендуем использовать
специальный способ
для её запоминания.
Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону.
(a + b)(a2 − ab + b2)
= a3 + b3
Как разложить на множители сумму кубов
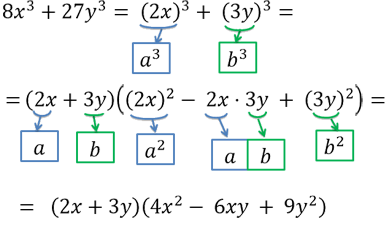
Рассмотрим пример. Необходимо разложить на множители сумму кубов.
Обратим внимание, что «8x3» — это
«(2x)3», значит, для формулы суммы кубов
вместо «a» мы используем «2x».
Используем формулу суммы кубов. Только вместо «a3» у
нас будет «8x3», а вместо
«b3» будет
«27y3».
Применение суммы кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в сумму кубов, используя формулу сокращенного
умножения.
Обратите внимание, что произведение многочленов
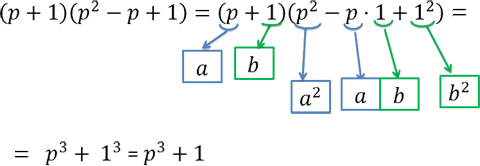
«(p + 1)(p2 − p + 1)» напоминает правую часть формулы суммы кубов
«a3 + b3 = (a + b)(a2 − ab + b2)»,
только вместо «a» стоит «p»,
а на месте «b» стоит «1».
Используем для произведения многочленов «(p + 1)(p2 − p + 1)» формулу сумму кубов в обратную сторону.
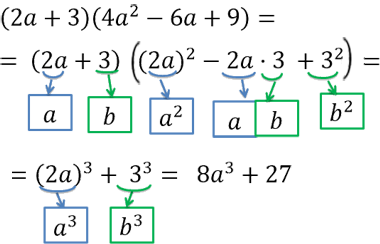
Рассмотрим пример сложнее. Требуется упростить произведение многочленов.
В этом произведении многочленов не так очевидно, что будет являться в формуле
«a», а что «b».
Если сравнить «(2a + 3)(4a2 − 6a + 9)» с
правой частью формулы суммы кубов
«a3 + b3 = (a + b)(a2 − ab + b2),
то можно понять, что в первой скобке «(2a + 3)»
на месте «a» стоит «2a», а на месте «b»
стоит «3».
Теперь представим скобку «(4a2 − 6a + 9)» таким образом, чтобы
она соответствовала правой части формулы суммы кубов.
Используем формулу суммы кубов и решим пример до конца.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Сумма кубов
В алгебре формулы сокращенного умножения — тождества, то есть любая из формул верна как для перехода от правой части к левой, так и от левой к правой.
Мы выяснили, что произведение суммы двух выражений и неполного квадрата разности равно сумме кубов этих выражений. И обратно,
сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Формула суммы кубов:
С помощью схемы сумму кубов можно представить так:
Например,
На практике, чтобы пользоваться формулой суммы кубов, ее надо научиться видеть.
Например, в сумме
сначала надо увидеть, что 1000 — это куб 10, а 27y³ — куб (3y):
и только потом расписать его как сумму кубов:
На первом этапе изучения формулы можно использовать схему.
Например,
Таблица кубов от 1 до 10 поможет нам увидеть кубы чисел:
Свойство степеней поможет определить куб степени:
Рассмотрим еще примеры разложения по формуле суммы кубов.
Чтобы определить, сколько цифр после запятой нужно записать в десятичной дроби, если известен ее куб, надо количество знаков после запятой в кубе числа разделить на 3:
В алгебре формулу суммы кубов чаще всего используют для упрощения действия разложения многочленов на множители.

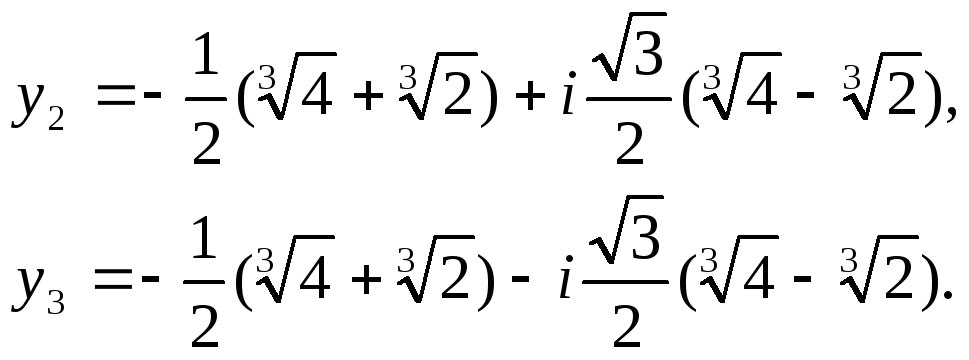
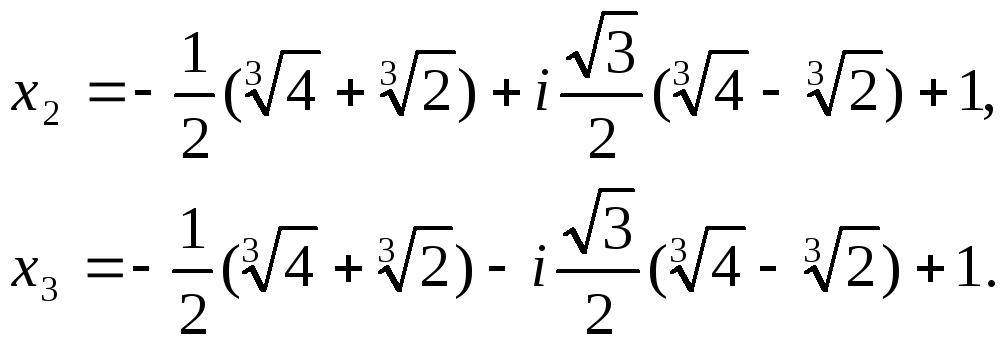
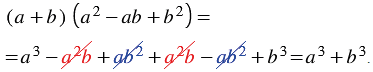
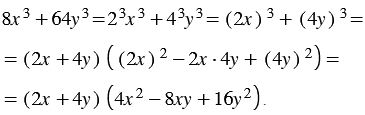
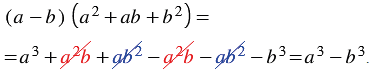
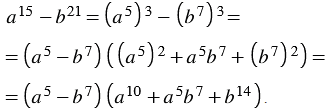
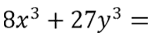
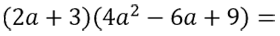

![Rendered by QuickLaTeX.com [{begin{array}{*{20}{l}} {{1^3} = 1}\ {{2^3} = 8}\ {{3^3} = 27}\ {{4^3} = 64}\ {{5^3} = 125}\ {{6^3} = 216}\ {{7^3} = 343}\ {{8^3} = 512}\ {{9^3} = 729}\ {{{10}^3} = 1000} end{array}}]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-33cbab67d13c74f4aa853af0ed4194cd_l3.png)
![Rendered by QuickLaTeX.com [ = (frac{3}{2}{a^2} + 4)(frac{9}{4}{a^4} - frac{{3 cdot mathop {overline 4 }limits^2 }}{{mathop {underline 2 }limits_1 }}{a^2} + 16) = ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-cd5395eea8965778a665f974a6717ad3_l3.png)