17 авг. 2022 г.
читать 2 мин
Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионной модели.
Он рассчитывается как:
Остаток = наблюдаемое значение – прогнозируемое значение
Один из способов понять, насколько хорошо регрессионная модель соответствует набору данных, — вычислить остаточную сумму квадратов , которая рассчитывается как:
Остаточная сумма квадратов = Σ(e i ) 2
куда:
- Σ : греческий символ, означающий «сумма».
- e i : i -й остаток
Чем ниже значение, тем лучше модель соответствует набору данных.
В этом руководстве приведены примеры расчета суммы квадратов остатков для простой модели линейной регрессии и модели множественной линейной регрессии в Excel.
Пример 1: Остаточная сумма квадратов для простой линейной регрессии
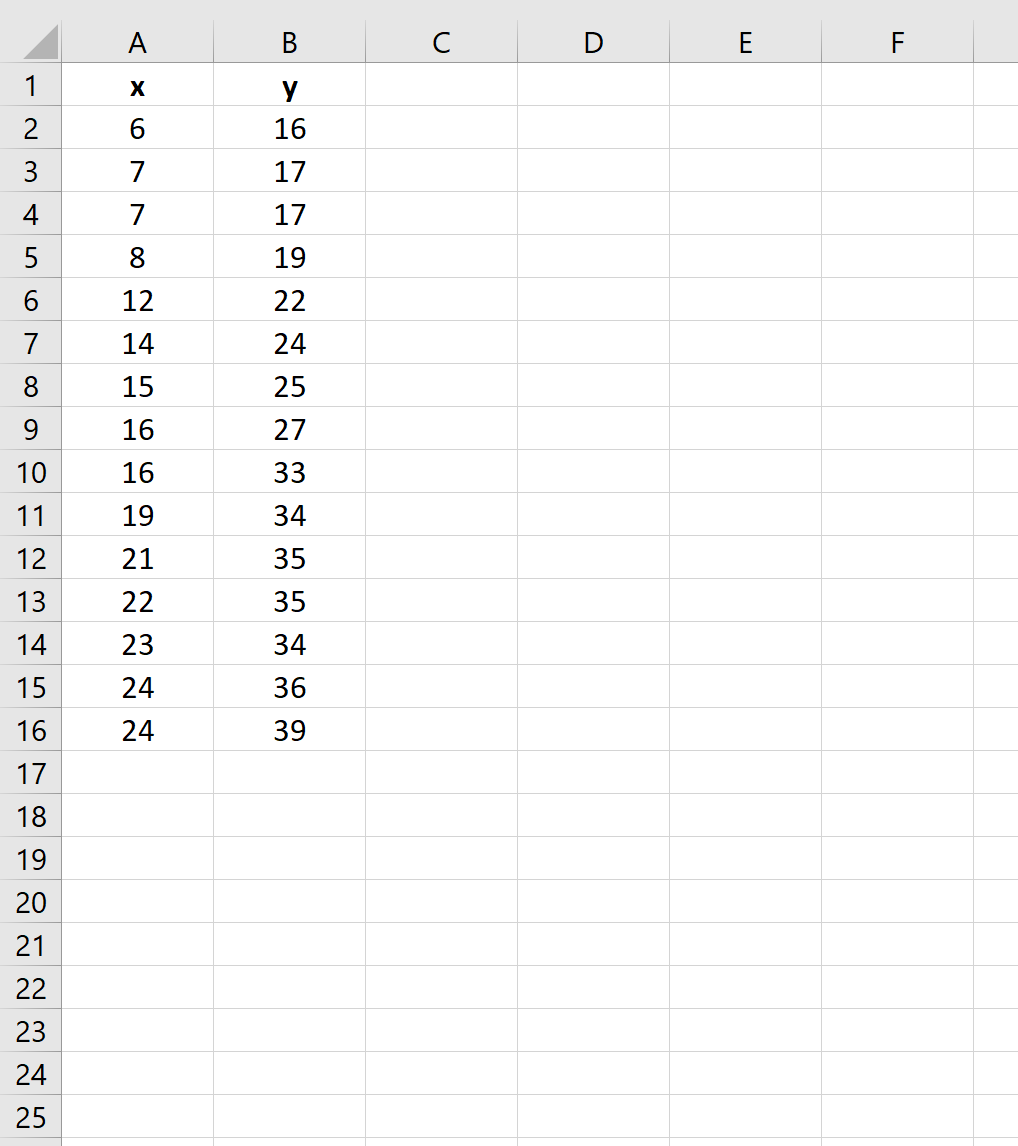
Предположим, у нас есть следующий набор данных в Excel:
Чтобы вычислить остаточную сумму квадратов для простой модели линейной регрессии, используя x в качестве переменной предиктора и y в качестве переменной ответа, мы можем использовать функцию ЛИНЕЙН() , которая использует следующий синтаксис:
ЛИНЕЙН(известные_ys, [известные_xs], [const], [статистика])
куда:
- known_ys: диапазон значений y
- known_sx: диапазон значений x.
- const: принуждать ли константу b к нулю. Мы оставим это поле пустым.
- stats: список статистики регрессии. Мы укажем, что это TRUE.
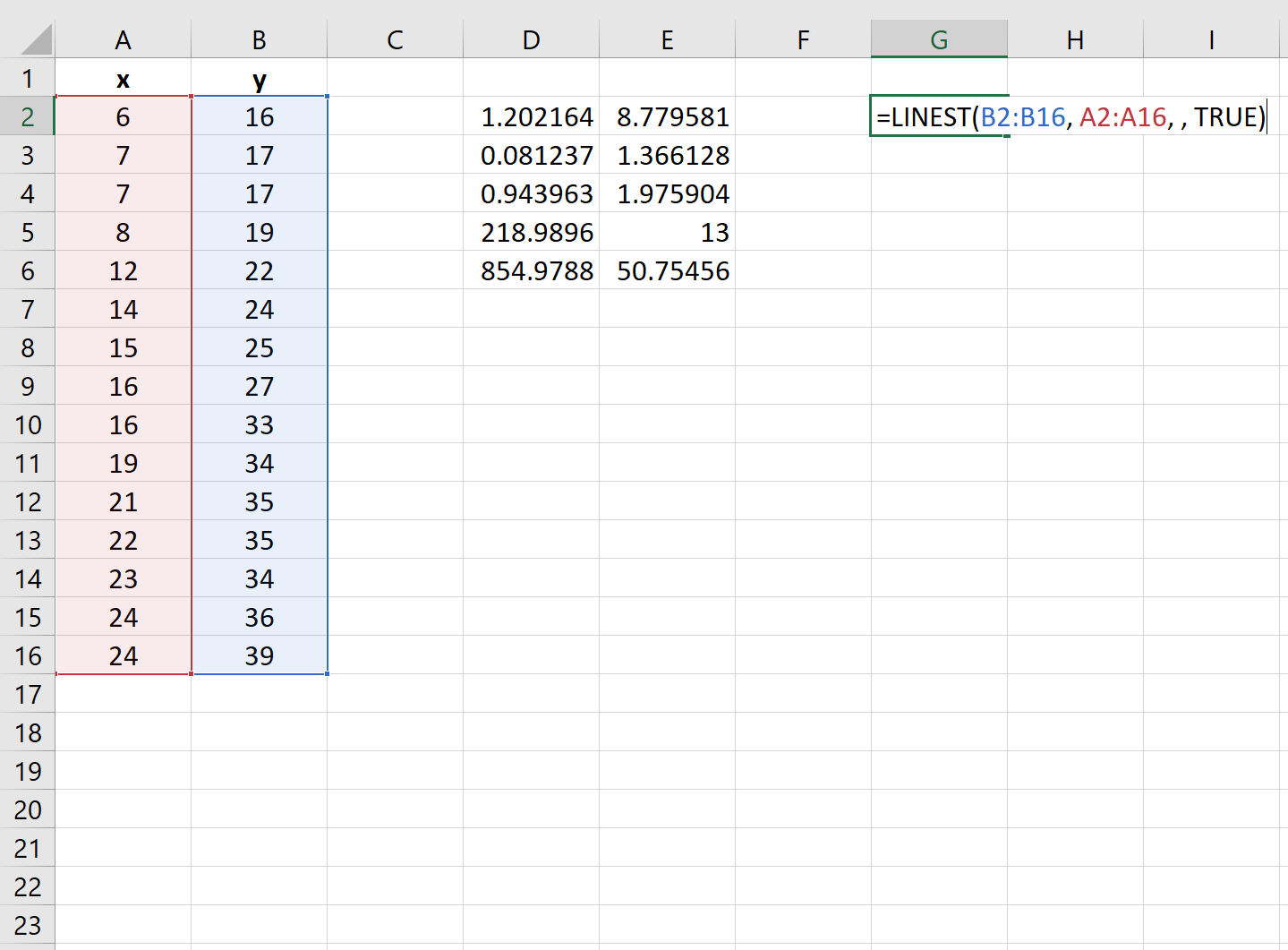
На следующем снимке экрана показано, как использовать эту функцию на практике:
Остаточная сумма квадратов для регрессионной модели отображается в последней ячейке второго столбца выходных данных. В этом примере остаточная сумма квадратов оказывается равной 50,75 .
Пример 2: Остаточная сумма квадратов для множественной линейной регрессии
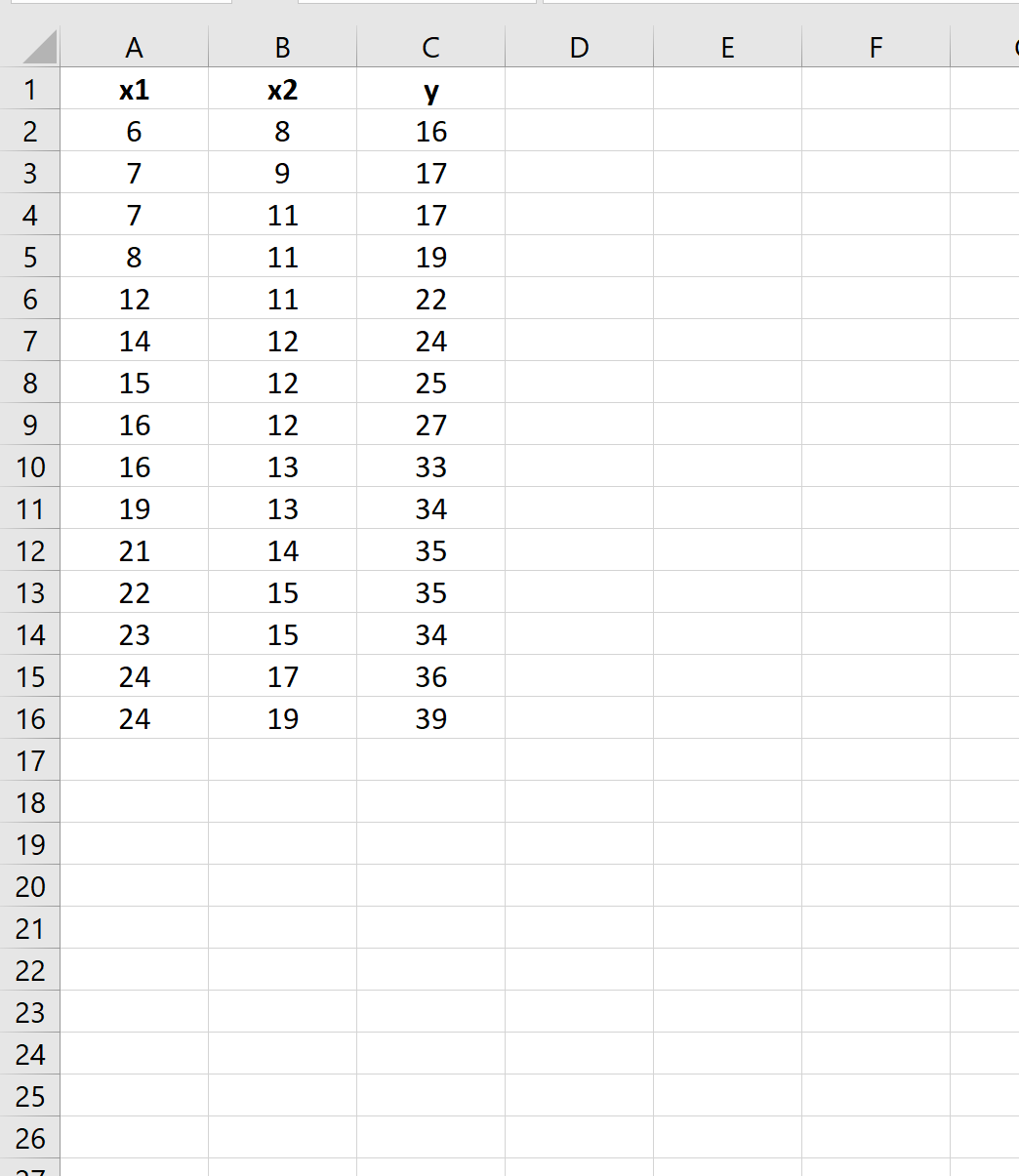
Предположим, у нас есть следующий набор данных в Excel:
Мы снова можем использовать функцию ЛИНЕЙН() для вычисления остаточной суммы квадратов для модели.
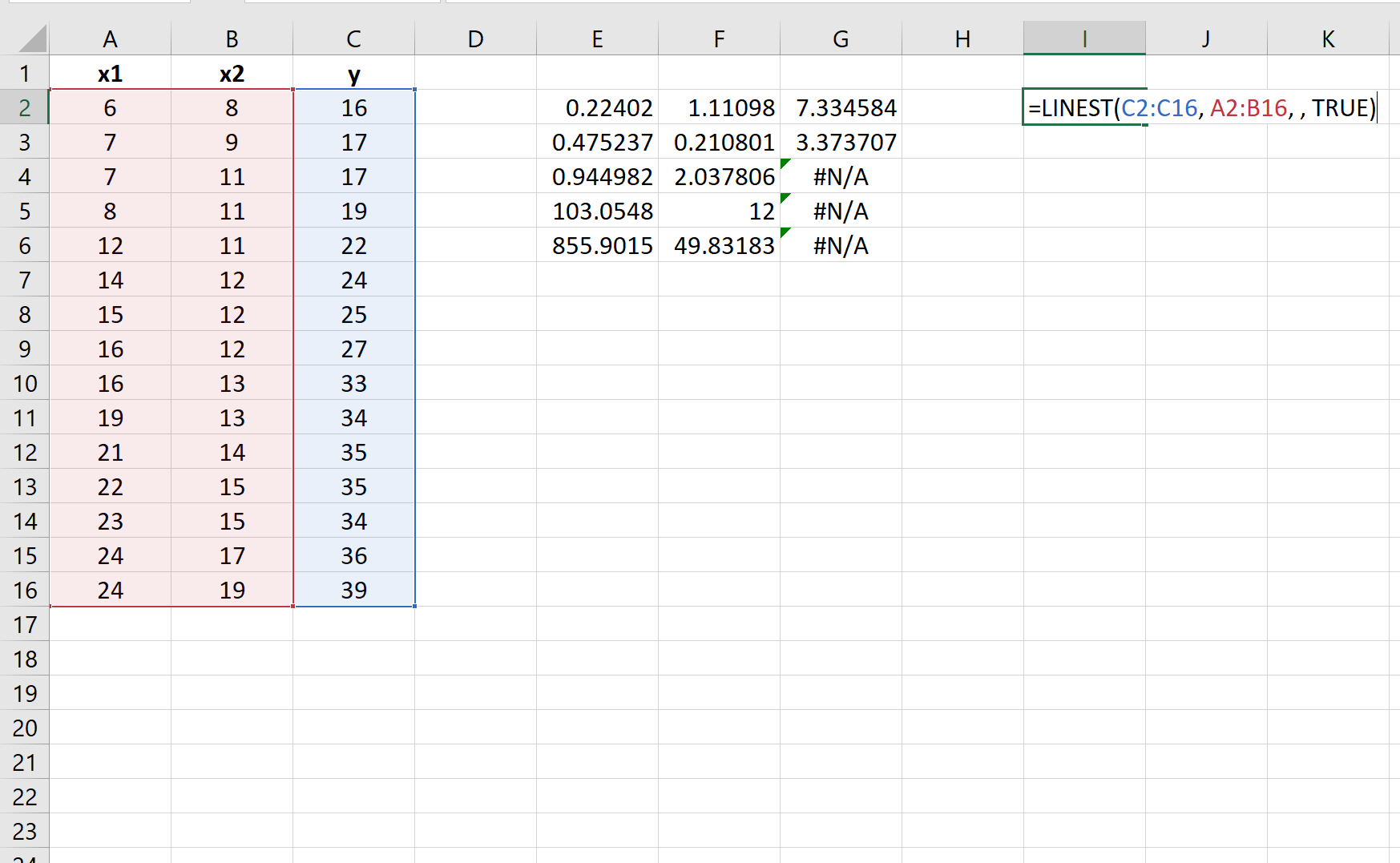
Единственное отличие состоит в том, что мы укажем два столбца значений для аргумента known_xs :
Остаточная сумма квадратов для этой модели множественной линейной регрессии оказывается равной 49,83 .
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Калькулятор остаточной суммы квадратов
From Wikipedia, the free encyclopedia
In statistics, the residual sum of squares (RSS), also known as the sum of squared residuals (SSR) or the sum of squared estimate of errors (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model, such as a linear regression. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection.
In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model.
One explanatory variable[edit]
In a model with a single explanatory variable, RSS is given by:[1]
where yi is the ith value of the variable to be predicted, xi is the ith value of the explanatory variable, and 

In a standard linear simple regression model, 



where 



Matrix expression for the OLS residual sum of squares[edit]
The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is
where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators, 

The residual vector 
,
(equivalent to the square of the norm of residuals). In full:
,
where H is the hat matrix, or the projection matrix in linear regression.
Relation with Pearson’s product-moment correlation[edit]
The least-squares regression line is given by
,
where 



Therefore,
where 
The Pearson product-moment correlation is given by 

See also[edit]
- Akaike information criterion#Comparison with least squares
- Chi-squared distribution#Applications
- Degrees of freedom (statistics)#Sum of squares and degrees of freedom
- Errors and residuals in statistics
- Lack-of-fit sum of squares
- Mean squared error
- Reduced chi-squared statistic, RSS per degree of freedom
- Squared deviations
- Sum of squares (statistics)
References[edit]
- ^ Archdeacon, Thomas J. (1994). Correlation and regression analysis : a historian’s guide. University of Wisconsin Press. pp. 161–162. ISBN 0-299-13650-7. OCLC 27266095.
- Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 0-471-17082-8.
Что такое остаточная сумма квадратов?
Остаточная сумма квадратов (RSS) — это статистический метод, который помогает определить уровень несоответствия в наборе данных, не предсказанный регрессионной моделью. Таким образом, он измеряет дисперсию значения наблюдаемых данных по сравнению с его прогнозируемым значением в соответствии с моделью регрессии. Следовательно, RSS указывает, хорошо ли модель регрессии соответствует фактическому набору данных или нет.
Также называемая суммой квадратов ошибок (SSE), RSS получается путем сложения квадрата остатков. Остатки представляют собой предполагаемые отклонения от фактических значений данных и представляют ошибки в регрессии Регрессия Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать дальшеоценка модели. Более низкий RSS указывает на то, что модель регрессии хорошо соответствует данным и имеет минимальную вариацию данных. В финансах Финансы — это широкий термин, который по существу относится к управлению капиталом или направлению денег для различных целей. Более того, инвесторы используют RSS для отслеживания изменений цен на акции, чтобы предсказать их будущие движения цен.
Оглавление
- Что такое остаточная сумма квадратов?
- Объяснение остаточной суммы квадратов
- Остаточная сумма квадратов в финансах
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Остаточная сумма квадратов (RSS) — это статистический метод, используемый для измерения отклонения в наборе данных, не объясненного регрессионной моделью.
- Остаток или ошибка — это разница между фактическим и прогнозируемым значением наблюдения.
- Если значение RSS низкое, это означает, что данные хорошо соответствуют модели оценки, что указывает на наименьшую дисперсию. Если он равен нулю, модель идеально соответствует данным, не имея вообще никакой дисперсии.
- Это помогает игрокам фондового рынка оценивать будущие движения цен на акции, отслеживая колебания цен на акции.
Объяснение остаточной суммы квадратов
RSS — это один из типов суммы квадратов (SS), остальные два — это общая сумма квадратов (TSS) и сумма квадратов из-за регрессии (SSR) или объясненная сумма квадратов (ESS). Сумма квадратов — это статистическая мера, посредством которой дисперсия данных. Дисперсия В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Читать далее оценивается, чтобы определить, насколько хорошо данные будут соответствовать модели в регрессионном анализе.
В то время как TSS измеряет изменение значений наблюдаемой переменной по отношению к ее выборочному среднему, SSR или ESS вычисляют отклонение между оценочным значением и средним значением наблюдаемой переменной. Если TSS равен SSR, это означает, что модель регрессии идеально подходит для данных, поскольку она отражает всю изменчивость фактических данных.
С другой стороны, RSS измеряет степень изменчивости наблюдаемых данных, не отображаемых регрессионной моделью. Чтобы вычислить RSS, сначала найдите уровень ошибки или остатка модели, вычитая фактические наблюдаемые значения из оценочных значений. Затем возведите в квадрат и сложите все значения ошибок, чтобы получить RSS.
Чем ниже ошибка модели, тем лучше прогноз регрессии. Другими словами, более низкий RSS означает, что регрессионная модель лучше объясняет данные, указывая на наименьшую дисперсию. Это означает, что модель хорошо соответствует данным. Аналогичным образом, если значение достигает нуля, оно считается наиболее подходящим без отклонений.
Обратите внимание, что RSS не похож на R-SquaredR-SquaredR-squared (R2 или коэффициент детерминации) — это статистическая мера, которая показывает степень вариации зависимой переменной из-за независимой переменной. Подробнее. В то время как первый определяет точную величину вариации, R-квадрат — это величина вариации, определяемая относительно доли общей вариации.
Остаточная сумма квадратов в финансах
Несоответствие, обнаруженное в наборе данных через RSS, указывает, соответствуют ли данные регрессионной модели или нет. Таким образом, это помогает фондовому рынкуФондовый рынокФондовый рынок работает по основному принципу согласования спроса и предложения посредством аукционного процесса, когда инвесторы готовы заплатить определенную сумму за актив и они готовы продать то, что у них есть, по определенной цене. узнайте больше игроков, чтобы понять колебания цен на активы, что позволит им оценить свои будущие движения цен.
Функции регрессии формируются для прогнозирования движения цен акций. Но польза от этих регрессионных моделей зависит от того, хорошо ли они объясняют колебания цен на акции. Однако если в модели есть ошибки или остатки, не объясняемые регрессией, то модель может оказаться бесполезной для прогнозирования движения запасов в будущем.
В результате инвесторы и инвестиционные менеджеры получают возможность принимать оптимальные и наиболее взвешенные решения с помощью RSS. Кроме того, RSS также позволяет политикам анализировать различные переменные, влияющие на экономическую стабильность страны, и соответствующим образом формировать экономические модели.
Формула
Вот формула для вычисления остаточной суммы квадратов:
Где,
Пример расчета
Рассмотрим следующее остаточная сумма квадратов пример на основе набора данных ниже:
Абсолютную дисперсию можно легко узнать, применив приведенную выше формулу RSS:
= {1 – [1+(2*0)]}2 + {2 – [1+(2*1)]}2 + {6 – [1+(2*2)]}2 + {8 – [1+(2*3)]}2
= 0+1+1+1 = 3
Часто задаваемые вопросы (FAQ)
Что такое остаточная сумма квадратов (RSS)?
RSS — это статистический метод, используемый для определения уровня несоответствия в наборе данных, не выявленного с помощью регрессии. Если остаточная сумма квадратов приводит к меньшему значению, это означает, что модель регрессии объясняет данные лучше, чем когда результат выше. На самом деле, если его значение равно нулю, оно считается наилучшим соответствием без каких-либо ошибок.
В чем разница между ESS и RSS?
ESS расшифровывается как «Объясненная сумма квадратов», что означает изменение данных, объясненное регрессионной моделью. С другой стороны, остаточная сумма квадратов (RSS) определяет вариации, отмеченные несоответствиями в наборе данных, не объясняемыми моделью оценки.
Чем отличаются TSS и RSS?
Общая сумма квадратов (TSS) определяет отклонения наблюдаемых значений или наборов данных от среднего значения. Напротив, остаточная сумма квадратов (RSS) оценивает ошибки или расхождения в наблюдаемых данных и смоделированных данных.
Рекомендуемые статьи
Это было руководство к тому, что такое остаточная сумма квадратов. Здесь мы объясняем, как рассчитать остаточную сумму квадратов в регрессии с помощью формулы и примера. Подробнее об этом вы можете узнать из следующих статей —
- Регрессия методом наименьших квадратовРегрессия методом наименьших квадратовКвадратный корень в VBA представляет собой математическую/триггерную функцию Excel, которая возвращает квадратный корень из введенного числа. Для этой функции квадратного корня используется терминология SQRT. Например, с помощью этой функции VBA пользователь может определить квадратный корень из 70 как 8,366602.Подробнее
- Gradient BoostingGradient BoostingGradient Boosting — это система повышения машинного обучения, представляющая собой дерево решений для больших и сложных данных. Он основан на предположении, что следующая возможная модель сведет к минимуму грубую ошибку прогноза в сочетании с предыдущим набором моделей.Подробнее
- Линия регрессииЛиния регрессииЛиния регрессии показывает линейную связь между зависимыми переменными на оси Y и независимыми переменными на оси X. Корреляция устанавливается путем анализа шаблона данных, сформированного переменными.Подробнее
Вычисление
остатков производим с помощью СервисАнализ
данныхРегрессия
(п.1)
Таблица
4
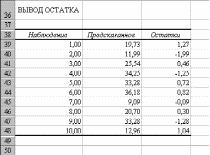
Остаточная
сумма квадратов:
∑e(t)Это
значение можно найти в третьем столбце
таблицы 2, равное – 11,35.
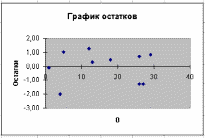
Дисперсия
остатков S2
2
= 1,42 (значение из 4 столбца таблицы 2).
3.
Проверить
выполнение предпосылок МНК.
Предпосылки
МНК:
1)
В задании у
(объем выпуска продукции) является
результативным признаком, а х1
(объем
капиталовложений) – факторным признаком.
2)
Так как у нас парная регрессия, то
отсутствие мультиоколлинеарности
выполняется автоматически.
3)
Наличие (отсутствие) автокорреляции в
отклонениях проверяют с помощью критерия
Дарбина-Уотсона. Численное значение
коэффициента равно:
|
dw= |
(i-i-1) |
, |
|||||
|
2i |
|||||||
|
t |
y |
y |
εi= |
εi2 |
εi-1 |
εi |
(εi |
|
1 |
21,0000 |
21,4454 |
-0,4454 |
0,1984 |
|||
|
2 |
10,0000 |
10,8655 |
-0,8655 |
0,7491 |
-0,4454 |
-0,4201 |
0,1765 |
|
3 |
26,0000 |
24,1743 |
1,8257 |
3,3332 |
-0,8655 |
2,6912 |
7,2426 |
|
4 |
33,0000 |
33,0756 |
-0,0756 |
0,0057 |
1,8257 |
-1,9013 |
3,6148 |
|
5 |
34,0000 |
33,7793 |
0,2207 |
0,0487 |
-0,0756 |
0,2962 |
0,0878 |
|
6 |
37,0000 |
39,5442 |
-2,5442 |
6,4729 |
0,2207 |
-2,7649 |
7,6445 |
|
7 |
9,0000 |
10,3592 |
-1,3592 |
1,8476 |
-2,5442 |
1,1849 |
1,4041 |
|
8 |
21,0000 |
19,2730 |
1,7270 |
2,9824 |
-1,3592 |
3,0862 |
9,5246 |
|
9 |
32,0000 |
35,0505 |
-3,0505 |
9,3053 |
1,7270 |
-4,7774 |
22,8237 |
|
10 |
14,0000 |
9,4329 |
4,5671 |
20,8584 |
-3,0505 |
7,6176 |
58,0273 |
|
45,8017 |
-4,5671 |
5,0125 |
110,5458 |
dw
= 110,5458 / 45,8017 = 2,4135
Определим
выполняется МНК или нет:
1,08
1,36 2
На
оси найдем точку dw = 2,4135, она находится
в IV области. Следовательно, можно сделать
вывод о том, что автокорреляция остатков
в ряду динамики присутствует.
4)
Равенство математического ожидания
остатков 0 проверяется по t-критерию
Стьюдента.
Проанализировав
сумму остатков (таблица 4) получили -1,33
* 10-14
/
10 ≈ 0. значит t = (׀
Ē
׀/
SE)*
√ n
→ 0, следовательно, данная предпосылка
МНК выполняется, так как tтабл
= 2,31 > t
5)
Постоянная дисперсия (т.е. выполнение
свойства гомоскедастичности по тесту
Голдфельда-Квандта)
Упорядочим
n наблюдений по мере возрастания переменой
х.
Разделим
исходный блок на 3 части, причем 1 3 части
равны по размеру n = 4
2
часть из рассмотрения исключается.
Для
1 и 3 частей строится уравнения регрессии.
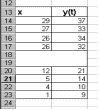
1
уравнение



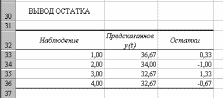
2
уравнение




Следовательно
уравнения регрессии будут иметь вид:
у1
= 0,048 + 0,796х1
у2
=
-2 + 1,33х1
По
уравнениям регрессии определяется
остаточная дисперсия. Сравнение дисперсий
происходит по F-критерию Фишера.
Если
Fнаблюд.
=S1ŷ/S2ŷ
>Fкр.(a;k1;k2),
то
выполняется свойство гомоскедастичности
(ГО)
Если
F расч
>
F табл,
то
имеет место гетероскедастичность (ГЕ).
Чтобы
найти значение F табл
данного критерия определим степени
свободы по формуле
К1=К2=(n-C-2*p)/2
n=10,
C=2
– количество исключаемых наблюдений
во 2 части блока исходных данных
р=1
– число факторов
К1=К2=(10-2-2*1)/2
= 3
F
табл
= 10,13
Найдем
F расч
σ2
= ∑
εi2
/
(n-1)
σ2(1
ур.) = 3,33 / 9 = 0,37
σ2(2
ур.) = 4,75 / 9 = 0,53
F
расч
=
0,53 / 0,37 = 1,4324
Так
как F расч
<
F табл
,
то можно сказать что больше нарушена
предпосылка о равенстве дисперсий
остаточных величин и следовательно
выполняется свойство гомоскедастичности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике, то остаточная сумма квадратов ( RSS), также известные как сумма квадратов остатков ( SSR) или сумму квадратов оценки ошибок ( SSE), является суммой из квадратов из остатков (отклонения предсказывали от реальных эмпирических значений данных). Это мера расхождения между данными и моделью оценки, такой как линейная регрессия. Небольшой RSS указывает на точное соответствие модели данным. Он используется как критерий оптимальности при выборе параметров и выбора модели.
В общем, общая сумма квадратов = объясненная сумма квадратов + остаточная сумма квадратов. Для доказательства этого в многомерном обычном случае наименьших квадратов (OLS) см. Разделение в общей модели OLS.
СОДЕРЖАНИЕ
- 1 Одна объясняющая переменная
- 2 Матричное выражение для остаточной суммы квадратов OLS
- 3 Связь с корреляцией продукта и момента Пирсона
- 4 См. Также
- 5 ссылки
Одна объясняющая переменная
В модели с единственной независимой переменной RSS задается следующим образом:
- RSS знак равно ∑ я знак равно 1 п ( у я — ж ( Икс я ) ) 2 { displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2}}
где y i — это i- е значение переменной, которую нужно спрогнозировать, x i — это i- е значение объясняющей переменной, и — это предсказанное значение y i (также называемое). В стандартной линейной простой модели регрессии, где и являются коэффициентами, у и х являются regressand и регрессор, соответственно, а ε является вектор ошибок. Сумма квадратов остатков — это сумма квадратов ; это ж ( Икс я ) { displaystyle f (x_ {i})}




- RSS знак равно ∑ я знак равно 1 п ( ε ^ я ) 2 знак равно ∑ я знак равно 1 п ( у я — ( α ^ + β ^ Икс я ) ) 2 { displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} ({ widehat { varepsilon ,}} _ {i}) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} — ({ widehat { alpha ,}} + { widehat { beta ,}} x_ {i})) ^ {2}}
где — оценочное значение постоянного члена, а — оценочное значение коэффициента наклона. α ^ { displaystyle { widehat { alpha ,}}}


Матричное выражение для остаточной суммы квадратов OLS
Общая регрессионная модель с n наблюдениями и k объяснителями, первый из которых представляет собой постоянный единичный вектор, коэффициент которого является пересечением регрессии, имеет вид
- у знак равно Икс β + е { Displaystyle у = Х бета + е}
где y — вектор наблюдений зависимой переменной размера n × 1, каждый столбец матрицы X размера n × k — вектор наблюдений на одном из k объяснителей, — вектор истинных коэффициентов k × 1, а e — размер n × 1 вектор истинных основных ошибок. В обычный метод наименьших квадратов Оценщик IS β { displaystyle beta}
- Икс β ^ знак равно у ⟺ { Displaystyle Х { шляпа { бета}} = у iff}
- Икс Т Икс β ^ знак равно Икс Т у ⟺ { displaystyle X ^ { operatorname {T}} X { hat { beta}} = X ^ { operatorname {T}} y iff}
- β ^ знак равно ( Икс Т Икс ) — 1 Икс Т у . { displaystyle { hat { beta}} = (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y.}
Остаточный вектор = ; поэтому остаточная сумма квадратов равна: е ^ { displaystyle { hat {e}}}
- RSS знак равно е ^ Т е ^ знак равно ‖ е ^ ‖ 2 { displaystyle operatorname {RSS} = { hat {e}} ^ { operatorname {T}} { hat {e}} = | { hat {e}} | ^ {2}}
,
(эквивалентно квадрату нормы остатков). В полном объеме:
- RSS знак равно у Т у — у Т Икс ( Икс Т Икс ) — 1 Икс Т у знак равно у Т [ я — Икс ( Икс Т Икс ) — 1 Икс Т ] у знак равно у Т [ я — ЧАС ] у { displaystyle operatorname {RSS} = y ^ { operatorname {T}} yy ^ { operatorname {T}} X (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y = y ^ { operatorname {T}} [IX (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}}] y = y ^ { имя оператора {T}} [IH] y}
,
где H — матрица шляпы или матрица проекции в линейной регрессии.
Связь с корреляцией продукта и момента Пирсона
Линия регрессии методом наименьших квадратов определяется выражением
- у знак равно а Икс + б { displaystyle y = ax + b}
,
где и, где и б знак равно у ¯ — а Икс ¯ { displaystyle b = { bar {y}} — а { bar {x}}}


Следовательно,
- RSS знак равно ∑ я знак равно 1 п ( у я — ж ( Икс я ) ) 2 знак равно ∑ я знак равно 1 п ( у я — ( а Икс я + б ) ) 2 знак равно ∑ я знак равно 1 п ( у я — а Икс я — у ¯ + а Икс ¯ ) 2 знак равно ∑ я знак равно 1 п ( а ( Икс ¯ — Икс я ) — ( у ¯ — у я ) ) 2 знак равно а 2 S Икс Икс — 2 а S Икс у + S у у знак равно S у у — а S Икс у знак равно S у у ( 1 — S Икс у 2 S Икс Икс S у у ) { displaystyle { begin {align} operatorname {RSS} amp; = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} — (ax_ {i} + b)) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} -ax_ {i } — { bar {y}} + a { bar {x}}) ^ {2} \ [5pt] amp; = sum _ {i = 1} ^ {n} (a ({ bar {x }} — x_ {i}) — ({ bar {y}} — y_ {i})) ^ {2} = a ^ {2} S_ {xx} -2aS_ {xy} + S_ {yy} = S_ {yy} -aS_ {xy} = S_ {yy} left (1 — { frac {S_ {xy} ^ {2}} {S_ {xx} S_ {yy}}} right) end {выровнено} }}
где S у у знак равно ∑ я знак равно 1 п ( у ¯ — у я ) 2 . { displaystyle S_ {yy} = sum _ {i = 1} ^ {n} ({ bar {y}} — y_ {i}) ^ {2}.}
Соотношение произведение-момент Пирсона определяется следующим образом: р знак равно S Икс у S Икс Икс S у у ; { displaystyle r = { frac {S_ {xy}} { sqrt {S_ {xx} S_ {yy}}}};}
Смотрите также
- Информационный критерий Акаике # Сравнение методом наименьших квадратов
- Распределение хи-квадрат # Приложения
- Степени свободы (статистика) # Сумма квадратов и степеней свободы
- Ошибки и неточности в статистике
- Неподходящая сумма квадратов
- Среднеквадратичная ошибка
- Сниженная статистика хи-квадрат, RSS на степень свободы
- Квадратные отклонения
- Сумма квадратов (статистика)
Рекомендации
- Draper, NR; Смит, Х. (1998). Прикладной регрессионный анализ (3-е изд.). Джон Вили. ISBN 0-471-17082-8.









![{displaystyle operatorname {RSS} =y^{operatorname {T} }y-y^{operatorname {T} }X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y=y^{operatorname {T} }[I-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }]y=y^{operatorname {T} }[I-H]y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74199b1f2403dea7307f2a078fcfdb50d00b984)

![{displaystyle {begin{aligned}operatorname {RSS} &=sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}=sum _{i=1}^{n}(y_{i}-(ax_{i}+b))^{2}=sum _{i=1}^{n}(y_{i}-ax_{i}-{bar {y}}+a{bar {x}})^{2}\[5pt]&=sum _{i=1}^{n}(a({bar {x}}-x_{i})-({bar {y}}-y_{i}))^{2}=a^{2}S_{xx}-2aS_{xy}+S_{yy}=S_{yy}-aS_{xy}=S_{yy}left(1-{frac {S_{xy}^{2}}{S_{xx}S_{yy}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5836407a2da838f1c020ae822005a218a92daa56)








