Как найти сумму максимальных элементов в матрице

Полное условие задачи звучит так: дана матрица размером N*N, содержащая положительные и отрицательные числа. Напишите код поиска субматрицы с максимально возможной суммой.

Существует множество решений этой задачи. Мы начнем с метода грубой силы, а затем займемся оптимизацией.

Метод грубой силы: O(N⁶)

Подобно другим задачам, связанным с поиском максимума, у этой задачи есть простое решение. Достаточно проверить все субматрицы, вычислить сумму каждой и найти самую большую.

Чтобы проверить все субматрицы и избежать повторов. Придется пройтись по всем упорядоченным парам строк и затем по всем упорядоченным парам столбцов.

Это решение потребует O(N⁶) времени, так как необходимо проверить O(N⁴) матриц, а проверка одной матрицы занимает O(N²) времени.

Динамическое программирование: O(N⁴)

Обратите внимание, что предыдущее решение работает медленно из-за расчета суммы элементов матрицы — O(N²) — очень медленная операция. Можно ли сократить это время? Да! Мы можем уменьшить время computeSum до O(1).

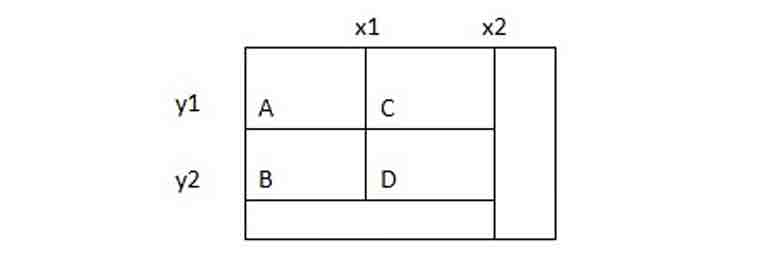
Посмотрите на следующий прямоугольник:

Предположим, что нам известны следующие значения:

ValD = area(point(0, 0) -> point(x2, y2))
ValC = area(point(0, 0) -> point(x2, yl))
ValB = area(point(0, 0) -> point(xl, y2))
ValA = area(point(0, 0) -> point(xl, yl))

Каждое Val* начинается в исходной точке и заканчивается в нижнем правом углу подпрямоугольника. Про эти значения мы знаем следующее:

area(D) = ValD - area(A union С) - area(A union B) + area(A).

Или:

area(D) = ValD - ValB - ValC + ValA

Данная информация позволит эффективно рассчитать эти значения для всех точек матрицы:

Уа1(х, у) = Уа1(х-1, у) + Уа1(у-1, х) - Уа1(х-1, у-1)

Можно заранее рассчитать подобные значения и затем найти максимальную субматрицу. Следующий код реализует данный алгоритм.

int getMaxMatrix(int[][] original) {
  int maxArea = Integer.MIN_VALUE; // Важно! Max может быть < 0
  int rowCount = original.length;
  int columnCount = original[0].length;
  int[][] matrix = precomputeMatrix(original);
  for (int rowl = 0; rowl < rowCount; rowl++) {
    for (int row2 = rowl; row2 < rowCount; row2++) {
      for (int coli = 0; coli < columnCount; coll++) {
        for (int col2 = coli; col2 < columnCount; col2++) {
          maxArea = Math.max(maxArea, computeSum(matrix, rowl, row2, coli, col2));
        }
      }
    }
  }
  return maxArea
}

int[][] precomputeMatrix(int[][] matrix) {
  int[][] sumMatrix = new int[matrix.length][matrix[0].length]; 
  for (int i = 0; i < matrix.length; i++) {
    for (int j = 0; j < matrix.length; j++) {
      if (i == 0 && j == 0) { // первая ячейка
        sumMatrix[i][j] = matrix[i][j];
      } else if (j == 0) { // ячейка в первой колонке
        sumMatrix[i][j] = sumMatrix[i - l][j] + matrix[i][j];
      } else if (i == 0) { // ячейка в первом ряду
        sumMatrix[i][j] = sumMatrix[i][j-1] + matrix[i][j]; 
      } else {
        sumMatrix[i][j] = sumMatrix[i-l][j] +
        sumMatrix[i][j-1] - sumMatrix[i-l][j-1] + 
        matrix[i][j];
      }
    }
  }
  return sumMatrix;
}

int computeSum(int[][] sumMatrix, int il, int i2, int jl, int j2) {
  if (il == 0 && jl == 0) { // начинаем с ряда 0, колонки 0
    return sumMatrix[i2][j2];
  } else if (il == 0) { // начинаем с ряда 0
    return sumMatrix[i2][j2] - sumMatrix[i2][jl - 1];
  } else if (jl == 0) { // начинаем с колонки 0
    return sumMatrix[i2][j2] - sumMatrix[il-l][j2];
  } else {
    return sumMatrix[i2][j2] - sumMatrix[i2][jl-1] - sumMatrix[il-l][j2] + sumMatrix[il-1][jl-1];
  }
}

Оптимизированное решение: O(N³)

Невероятно, но существует еще более оптимальное решение. Если у нас есть R строк и С столбцов, то задачу можно решить за О(R²C) времени.

Вспомните решение задачи про поиск максимального субмассива: для массива целых чисел (integer) найдите субмассив с максимальной суммой. Такой максимальный субмассив можно найти за О(N) времени. Давайте используем это решение для нашей задачи.

Каждую субматрицу можно представить в виде последовательности строк и последовательности столбцов. Можно пройтись по строкам и найти столбцы, дающие максимальную сумму.

Код будет таким:

maxSum = 0
foreach rowStart in rows
foreach rowEnd in rows
/* У нас есть количество возможных субматриц с границами 
* rowStart и rowEnd
* Найдите границы colStart и colEnd, дающие
* максимальную сумму. */
maxSum = max(runningMaxSum, maxSum)
return maxSum

Теперь остается вопрос: как найти «лучшие» colStart и colEnd?

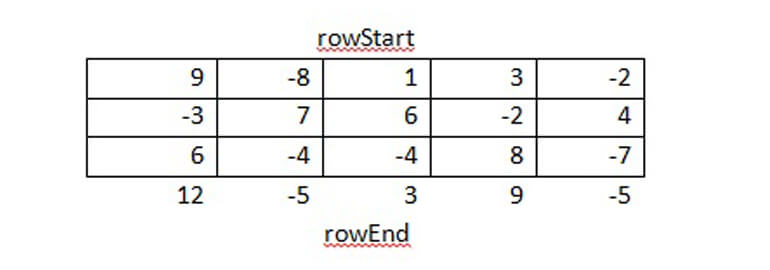
Рассмотрим субматрицу:

Нам необходимо найти colStart и colEnd, которые дают нам максимально возможную сумму всех субматриц rowStart сверху и rowEnd снизу. Можно вычислить сумму каждого столбца и использовать функцию maximumSubArray, которая обсуждалась в начале решения этой задачи.

В предыдущем примере максимальный субмасив охватывал пространство с первой по четвертую колонку. Это означает, что максимальная субматрица должна простираться от (rowStart, первый столбец) до (rowEnd, четвертый столбец).

Теперь мы можем записать следующий псевдокод:

maxSum = 0
foreach rowStart in rows
foreach rowEnd in rows
foreach col in columns
partialSum[col] = sum of matrix[rowStart, col] through
matrix[rowEnd, col]
runningMaxSum = maxSubArray(partialSum)
maxSum = max(runningMaxSum, maxSum)
return maxSum

Вычисление суммы в строках 5 и 6 занимает R*C времени (так как требует итерации от rowStart до rowEnd), что дает общее время выполнения О(R ³ C).

В строках 5 и 6 мы добавляли a[0]…a[i] с нуля, даже если на предыдущей итерации внешнего цикла добавились a[0]…a[i-1]. Давайте избавимся от двойной работы.

maxSum = 0
foreach rowStart in rows
clear array partialSum
foreach rowEnd in rows
foreach col in columns
partialSum[col] += matrix[rowEnd, col]
runningMaxSum = maxSubArray(partialSum)
maxSum = max(runningMaxSum, maxSum)
return maxSum

Полная версия кода выглядит так:

public void clearArray(int[] array) {
  for (int i = 0; i < array.length; i++) {
    array[i] = 0;
  }
}

public static int maxSubMatrix(int[][] matrix) {
  int rowCount = matrix.length;
  int colCount = matrix[0].length;

  int[] partialSum = new int[colCount];
  int maxSum = 0; // Макс, сумма = 0 (матрица пуста)

  for (int rowStart = 0; rowStart < rowCount; rowStart++) {
    clearArray(partialSum);

    for (int rowEnd = rowStart; rowEnd < rowCount; rowEnd++) {
      for (int i = 0; i < colCount; i++) {
        partialSum[i] += matrix[rowEnd][i]j
      }

      int tempMaxSum = maxSubArray(partialSum, colCount);

      /* Если вы хотите отслеживать координаты, добавьте
       * код здесь, чтобы сделать это. */
      maxSum = Math.max(maxSum, tempMaxSum);
    }
  }
  return maxSum;
}

public static int maxSubArray(int array[], int N) {
  int maxSum = 0;
  int runningSum = 0;

  for (int i = 0; i < N; i++) {
    runningSum += array[i];
    maxSum = Math.max(maxSum, runningSum);

    /*  Если runningSum < 0, нет смысла продолжать ряд
      * Сброс. */
    if  (runningSum < 0) {
      runningSum  = 0;
    }
  }
  return  maxSum;
}

Это чрезвычайно сложная задача. Вряд ли вы сможете решить подобную задачу на собеседовании без подсказки интервьюера.

Разбор задачи по книге «Карьера программиста. Как устроиться на работу в Google, Microsoft или другую ведущую IT-компанию»

Given an N*N matrix. The task is to find the index of a row with the maximum sum. That is the row whose sum of elements is maximum.

Examples: 

Input : mat[][] = {
            { 1, 2, 3, 4, 5 },
            { 5, 3, 1, 4, 2 },
            { 5, 6, 7, 8, 9 },
            { 0, 6, 3, 4, 12 },
            { 9, 7, 12, 4, 3 },
            }; 

Output : Row 3 has max sum 35

Input : mat[][] = { 
          { 1, 2, 3 },
          { 4, 2, 1 },
          { 5, 6, 7 },
          };
Output : Row 3 has max sum 18

The idea is to traverse the matrix row-wise and find the sum of elements in each row and check for every row if current sum is greater than the maximum sum obtained till the current row and update the maximum_sum accordingly. 

Algorithm:

• Define a constant N as the number of rows and columns in the matrix.
• Define a function colMaxSum that takes a 2D array of integers mat of size N*N as its input.
• Initialize two variables idx and maxSum to -1 and INT_MIN respectively.
• Traverse the matrix row-wise.
• For each row, calculate the sum of all the elements in that row.
• If the sum of the current row is greater than the current maxSum, update maxSum to be the sum of the current row and set idx to be the index of the current row.
• Return a pair of integers, with the first element being the index of the row with the maximum sum (idx) and the second element being the maximum sum (maxSum).

Pseudocode:

1. N ← number of rows and columns in the matrix
2. function colMaxSum(mat[N][N])
3.     idx ← -1
4.     maxSum ← INT_MIN
5.     for i from 0 to N-1
6.         sum ← 0
7.         for j from 0 to N-1
8.             sum ← sum + mat[i][j]
9.         if sum > maxSum
10.            maxSum ← sum
11.            idx ← i
12.    return pair(idx, maxSum)
13. end function

Below is the implementation of the above approach:

Row 3 has max sum 35

Time complexity: O(N²)
Auxiliary space: O(1)

Example in c:

Approach:

Initialize a variable max_sum to zero and a variable max_row to -1.

Traverse the matrix row by row:

a. Initialize a variable row_sum to zero.

b. Traverse the elements of the current row and add them to row_sum.

c. If row_sum is greater than max_sum, update max_sum to row_sum and max_row to the current row.

Return max_row.

Row with maximum sum is: 2

time complexity of O(mn) 

 space complexity of O(n)

Last Updated :
12 Apr, 2023

Like Article

Save Article

Перейти к содержанию

В
задачах подобного вида результатом
является единственное значение. Поэтому
начальные значения вычисляемым переменным
присваиваются
один раз — в начале алгоритма,
до организации циклов обработки
элементов массива. На
рис. 24 показан алгоритм вычисления
суммы элементов матрицы. Начальное
значение сумме
S=0
присваивается
до начала суммирования
элементов.
Затем обработка
элементов
массива
идёт по тому же
принципу, что и в предыдущем
пункте.

…

S:=0;

for
i:=1 to N do

for
j:=1 to M do

S
:= S+X[i,j];

writeln(‘S=
‘,S);

…
Рис. 24

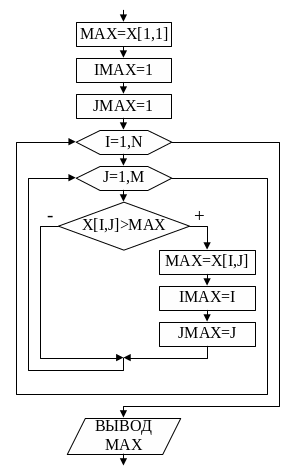
Т
акже
рассуждаем и при нахождении максимального
элемента матрицы
(рис. 25).
В качестве начального
значения максимума
принимаем
её первый элемент,
в качестве начальных значений координат
максимума — единицы. Затем поочерёдно
сравниваем максимум со всеми элементами
матрицы построчно и запоминаем координаты
вновь принятого
за максимум элемента. При завершении
обоих циклов максимум считается
окончательно найденным и может быть
обработан
по условию задачи. Ниже приведены
фрагменты программ,
иллюстрирующие рис. 25.

MAX
:= X[1,1];

Imax:=1;

Jmax:=1;

For
I:=1 to N do

For
j:=1 to M do

If
MAX < X[I,j] then

Begin

MAX:=
X[I,j];

Imax
:=I;

Jmax
:= j;

End;

Writeln(‘max=
‘,MAX);

…

Рис. 25

3.2.3. Нахождение суммы, произведения, максимума в каждой строке матрицы

При
решении задач подобного типа
в ответе получается столько же
значений, сколько в матрице строк.
Поэтому начальные значения
вычисляемым переменным присваиваем
при каждом переходе к
обработке следующей строки, т.е.
между циклами. Результат для каждой
строки также окончательно вычислен
при завершении каждой строки и может
быть обработан по условию задачи между
циклами (после
завершения цикла j).

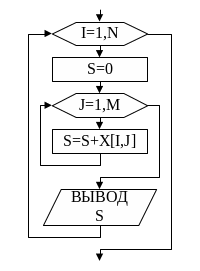
На
рис. 26 представлен алгоритм
нахождения суммы элементов каждой
строки матрицы X
и
вывод этих сумм на экран. Ниже приведены
фрагменты программ, иллюстрирующие
этот алгоритм.

…

for
i:=1 to N do

begin

S:=0;

for
j: =1 to M do

S:=S+X[
i , j ];

writeln(‘S=
^‘
,S);

end;

Рис. 26

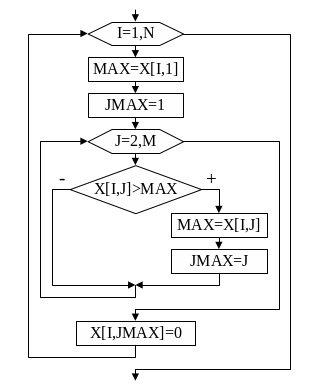
На
рис. 27 приведён алгоритм вычисления
максимума каждой строки матрицы X
и
замена
его нулём.

for
i:=l to N do

begin

MAX:=X[i,1]
; Jmax:=1;

for
j:=2 to M do

if
X[I,j] > MAX then

begin

MAX:=X[i,j];Jmax:=j
end;
X[i,Jmax] :=0;

end;

Рис.27

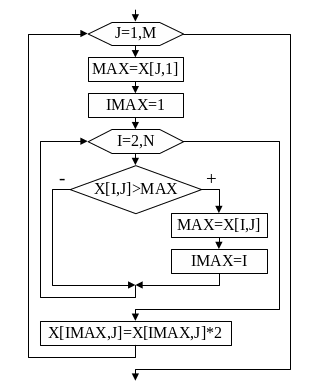
3.2.4. Алгоритм обработки элементов каждого столбца

При
решении задач подобного типа в ответе
получается столько
же значений, сколько в матрице столбцов.
В качестве примера
на рисунке 28 приведён алгоритм увеличения
в 2 раза
максимальных элементов столбцов матрицы
X.
Комментарии
к этому алгоритму аналогичны комментариям
к предыдущему
пункту. Ниже приведён фрагмент программы
к этому алгоритму.

f

or
j:=1 to M do

begin

МАХ:=Х[1,j];

Imax:=1;

for
i:=2 to N do if MAX<X[i,j] then

begin

MAX:=X[i,j];

Imax:=
i;

end;

X
[Imax, j ]: =X [Imax, j ] *2;

end;

… Рис.28

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #