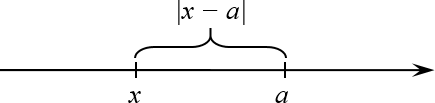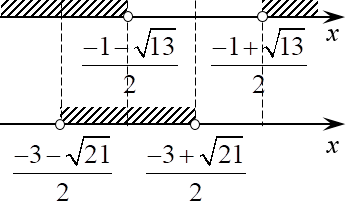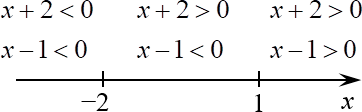Решение неравенств с модулем
4 февраля 2018
- Домашняя работа
- Ответы и решения
Сегодня, друзья, не будет никаких соплей и сантиментов. Вместо них я без лишних вопросов отправлю вас в бой с одним из самых грозных противников в курсе алгебры 8—9 класса.
Да, вы всё правильно поняли: речь идёт о неравенствах с модулем. Мы рассмотрим четыре основных приёма, с помощью которых вы научитесь решать порядка 90% таких задач. А что с остальными 10%? Что ж, о них мы поговорим в отдельном уроке.:)
Однако перед тем, как разбирать какие-то там приёмы, хотелось бы напомнить два факта, которые уже необходимо знать. Иначе вы рискуете вообще не понять материал сегодняшнего урока.
Что уже нужно знать
Капитан Очевидность как бы намекает, что для решения неравенств с модулем необходимо знать две вещи:
- Как решаются неравенства;
- Что такое модуль.
Начнём со второго пункта.
Определение модуля
Тут всё просто. Есть два определения: алгебраическое и графическое. Для начала — алгебраическое:
Определение. Модуль числа $x$ — это либо само это число, если оно неотрицательно, либо число, ему противоположное, если исходный $x$ — всё-таки отрицателен.
Записывается это так:
[left| x right|=left{ begin{align} & x, xge 0, \ & -x, x lt 0. \end{align} right.]
Говоря простым языком, модуль — это «число без минуса». И именно в этой двойственности (где-то с исходным числом ничего не надо делать, а где-то придётся убрать какой-то там минус) и заключается вся сложность для начинающих учеников.
Есть ещё геометрическое определение. Его тоже полезно знать, но обращаться к нему мы будем лишь в сложных и каких-то специальных случаях, где геометрический подход удобнее алгебраического (спойлер: не сегодня).
Определение. Пусть на числовой прямой отмечена точка $a$. Тогда модулем $left| x-a right|$ называется расстояние от точки $x$ до точки $a$ на этой прямой.
Если начертить картинку, то получится что-то типа этого:
Так или иначе, из определения модуля сразу следует его ключевое свойство: модуль числа всегда является величиной неотрицательной. Этот факт будет красной нитью идти через всё наше сегодняшнее повествование.
Решение неравенств. Метод интервалов
Теперь разберёмся с неравенствами. Их существует великое множество, но наша задача сейчас — уметь решать хотя бы самые простые из них. Те, которые сводятся к линейным неравенствам, а также к методу интервалов.
На эту тему у меня есть два больших урока (между прочем, очень, ОЧЕНЬ полезных — рекомендую изучить):
- Метод интервалов для неравенств (особенно посмотрите видео);
- Дробно-рациональные неравенства — весьма объёмный урок, но после него у вас вообще не останется каких-либо вопросов.
Если вы всё это знаете, если фраза «перейдём от неравенства к уравнению» не вызывает у вас смутное желание убиться об стену, то вы готовы: добро пожаловать в ад к основной теме урока.:)
1. Неравенства вида «Модуль меньше функции»
Это одна из самых часто встречающихся задач с модулями. Требуется решить неравенство вида:
[left| f right| lt g]
В роли функций $f$ и $g$ может выступать что угодно, но обычно это многочлены. Примеры таких неравенств:
[begin{align} & left| 2x+3 right| lt x+7; \ & left| {{x}^{2}}+2x-3 right|+3left( x+1 right) lt 0; \ & left| {{x}^{2}}-2left| x right|-3 right| lt 2. \end{align}]
Все они решаются буквально в одну строчку по схеме:
[left| f right| lt gRightarrow -g lt f lt gquad left( Rightarrow left{ begin{align} & f lt g, \ & f gt -g \end{align} right. right)]
Нетрудно заметить, что избавляемся от модуля, но взамен получаем двойное неравенство (или, что тоже самое, систему из двух неравенств). Зато этот переход учитывает абсолютно все возможные проблемы: если число под модулем положительно, метод работает; если отрицательно — всё равно работает; и даже при самой неадекватной функции на месте $f$ или $g$ метод всё равно сработает.
Естественно, возникает вопрос: а проще нельзя? К сожалению, нельзя. В этом вся фишка модуля.
Впрочем, хватит философствовать. Давайте решим парочку задач:
Задача. Решите неравенство:
[left| 2x+3 right| lt x+7]
Решение. Итак, перед нами классическое неравенство вида «модуль меньше» — даже преобразовывать нечего. Работаем по алгоритму:
[begin{align} & left| f right| lt gRightarrow -g lt f lt g; \ & left| 2x+3 right| lt x+7Rightarrow -left( x+7 right) lt 2x+3 lt x+7 \end{align}]
Не торопитесь раскрывать скобки, перед которыми стоит «минус»: вполне возможно, что из-за спешки вы допустите обидную ошибку.
[-x-7 lt 2x+3 lt x+7]
Поскольку дальше нужно решить каждое неравенство отдельно, пора переходить к системе (можно было сделать это и раньше, но тогда решение получится чуть более громоздким):
[left{ begin{align} & -x-7 lt 2x+3 \ & 2x+3 lt x+7 \ end{align} right.]
[left{ begin{align} & -3x lt 10 \ & x lt 4 \ end{align} right.]
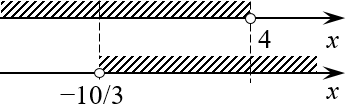
[left{ begin{align} & x gt -frac{10}{3} \ & x lt 4 \ end{align} right.]
Задача свелась к двум элементарным неравенствам. Отметим их решения на параллельных числовых прямых:
Пересечение множеств Пересечением этих множеств и будет ответ.
Ответ: $xin left( -frac{10}{3};4 right)$
Задача. Решите неравенство:
[left| {{x}^{2}}+2x-3 right|+3left( x+1 right) lt 0]
Решение. Это задание уже чуть посложнее. Для начала уединим модуль, перенеся второе слагаемое вправо:
[left| {{x}^{2}}+2x-3 right| lt -3left( x+1 right)]
Очевидно, перед нами вновь неравенство вида «модуль меньше», поэтому избавляемся от модуля по уже известному алгоритму:
[-left( -3left( x+1 right) right) lt {{x}^{2}}+2x-3 lt -3left( x+1 right)]
Вот сейчас внимание: кто-то скажет, что я немного извращенец со всеми этими скобками. Но ещё раз напомню, что наша ключевая цель — грамотно решить неравенство и получить ответ. Позже, когда вы в совершенстве освоите всё, о чём рассказано в этом уроке, можете сами извращаться как хотите: раскрывать скобки, вносить минусы и т.д.
А мы для начала просто избавимся от двойного минуса слева:
[-left( -3left( x+1 right) right)=left( -1 right)cdot left( -3 right)cdot left( x+1 right)=3left( x+1 right)]
Теперь раскроем все скобки в двойном неравенстве:
[3x+3 lt {{x}^{2}}+2x-3 lt -3x-3]
Переходим к двойному неравенству. В этот раз выкладки будут посерьёзнее:
[left{ begin{align} & {{x}^{2}}+2x-3 lt -3x-3 \ & 3x+3 lt {{x}^{2}}+2x-3 \ end{align} right.]
[left{ begin{align} & {{x}^{2}}+5x lt 0 \ & {{x}^{2}}-x-6 gt 0 \ end{align} right.]
Оба неравенства являются квадратными и решаются методом интервалов (потому и говорю: если не знаете, что это такое, лучше пока не браться за модули). Переходим к уравнению в первом неравенстве:
[begin{align} & {{x}^{2}}+5x=0; \ & xleft( x+5 right)=0; \ & {{x}_{1}}=0;{{x}_{2}}=-5. \end{align}]
Как видим, на выходе получилось неполное квадратное уравнение, которое решается элементарно. Теперь разберёмся со вторым неравенством системы. Там придётся применить теорему Виета:
[begin{align} & {{x}^{2}}-x-6=0; \ & left( x-3 right)left( x+2 right)=0; \& {{x}_{1}}=3;{{x}_{2}}=-2. \end{align}]
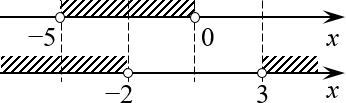
Отмечаем полученные числа на двух параллельных прямых (отдельная для первого неравенства и отдельная для второго):
Опять же, поскольку мы решаем систему неравенств, нас интересует пересечение заштрихованных множеств: $xin left( -5;-2 right)$. Это и есть ответ. Ответ: $xin left( -5;-2 right)$
Думаю, после этих примеров схема решения предельно ясна:
- Уединить модуль, перенеся все другие слагаемые в противоположную часть неравенства. Таким образом мы получим неравенство вида $left| f right| lt g$.
- Решить это неравенство, избавившись от модуля по описанной выше схеме. В какой-то момент потребуется перейти от двойного неравенства к системе из двух самостоятельных выражений, каждое из которых уже можно решать отдельно.
- Наконец, останется лишь пересечь решения этих двух самостоятельных выражений — и всё, мы получим окончательный ответ.
Аналогичный алгоритм существует и для неравенств следующего типа, когда модуль больше функции. Однако там есть парочка серьёзных «но». Об этих «но» мы сейчас и поговорим.
2. Неравенства вида «Модуль больше функции»
Выглядят они так:
[left| f right| gt g]
Похоже на предыдущее? Похоже. И тем не менее решаются такие задачи совсем по-другому. Формально схема следующая:
[left| f right| gt gRightarrow left[ begin{align} & f gt g, \ & f lt -g \end{align} right.]
Другими словами, мы рассматриваем два случая:
- Сначала просто игнорируем модуль — решаем обычное неравенство;
- Затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак.
При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.
Обратите внимание ещё раз: перед нами не система, а совокупность, поэтому в ответе множества объединяются, а не пересекаются. Это принципиальное отличие от предыдущего пункта!
Вообще, с объединениями и пересечениями у многих учеников сплошная путаница, поэтому давайте разберёмся в этом вопросе раз и навсегда:
- «∪» — это знак объединения. По сути, это стилизованная буква «U», которая пришла к нам из английского языка и является аббревиатурой от «Union», т.е. «Объединения».
- «∩» — это знак пересечения. Эта хрень ниоткуда не пришла, а просто возникла как противопоставление к «∪».
Чтобы ещё проще было запомнить, просто пририсуйте к этим знакам ножки, чтобы получились бокалы (вот только не надо сейчас обвинять меня в пропаганде наркомании и алкоголизма: если вы всерьёз изучаете этот урок, то вы уже наркоман):
В переводе на русский это означает следующее: объединение (совокупность) включает в себя элементы из обоих множеств, поэтому никак не меньше каждого из них; а вот пересечение (система) включает в себя лишь те элементы, которые одновременно находятся и в первом множестве, и во втором. Поэтому пересечение множеств никогда не бывает больше множеств-исходников.
Так стало понятнее? Вот и отлично. Переходим к практике.
Задача. Решите неравенство:
[left| 3x+1 right| gt 5-4x]
Решение. Действуем по схеме:
[left| 3x+1 right| gt 5-4xRightarrow left[ begin{align} & 3x+1 gt 5-4x \ & 3x+1 lt -left( 5-4x right) \end{align} right.]
Решаем каждое неравенство совокупности:
[left[ begin{align} & 3x+4x gt 5-1 \ & 3x-4x lt -5-1 \ end{align} right.]
[left[ begin{align} & 7x gt 4 \ & -x lt -6 \ end{align} right.]
[left[ begin{align} & x gt 4/7 \ & x gt 6 \ end{align} right.]
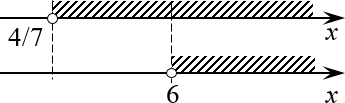
Отмечаем каждое полученное множество на числовой прямой, а затем объединяем их:
Объединение множеств Совершенно очевидно, что ответом будет $xin left( frac{4}{7};+infty right)$
Ответ: $xin left( frac{4}{7};+infty right)$
Задача. Решите неравенство:
[left| {{x}^{2}}+2x-3 right| gt x]
Решение. Ну что? Да ничего — всё то же самое. Переходим от неравенства с модулем к совокупности двух неравенств:
[left| {{x}^{2}}+2x-3 right| gt xRightarrow left[ begin{align} & {{x}^{2}}+2x-3 gt x \ & {{x}^{2}}+2x-3 lt -x \end{align} right.]
Решаем каждое неравенство. К сожалению, корни там будут не оч:
[begin{align} & {{x}^{2}}+2x-3 gt x; \ & {{x}^{2}}+x-3 gt 0; \ & D=1+12=13; \ & x=frac{-1pm sqrt{13}}{2}. \end{align}]
Во втором неравенстве тоже немного дичи:
[begin{align} & {{x}^{2}}+2x-3 lt -x; \ & {{x}^{2}}+3x-3 lt 0; \ & D=9+12=21; \ & x=frac{-3pm sqrt{21}}{2}. \end{align}]
Теперь нужно отметить эти числа на двух осях — по одной оси для каждого неравенства. Однако отмечать точки нужно в правильном порядке: чем больше число, тем дальше сдвигам точку вправо.
И вот тут нас ждёт подстава. Если с числами $frac{-3-sqrt{21}}{2} lt frac{-1-sqrt{13}}{2}$ всё ясно (слагаемые в числителе первой дроби меньше слагаемых в числителе второй, поэтому сумма тоже меньше), с числами $frac{-3-sqrt{13}}{2} lt frac{-1+sqrt{21}}{2}$ тоже не возникнет затруднений (положительное число заведомо больше отрицательного), то вот с последней парочкой всё не так однозначно. Что больше: $frac{-3+sqrt{21}}{2}$ или $frac{-1+sqrt{13}}{2}$? От ответа на этот вопрос будет зависеть расстановка точек на числовых прямых и, собственно, ответ.
Поэтому давайте сравнивать:
[begin{matrix} frac{-1+sqrt{13}}{2}vee frac{-3+sqrt{21}}{2} \ -1+sqrt{13}vee -3+sqrt{21} \ 2+sqrt{13}vee sqrt{21} \end{matrix}]
Мы уединили корень, получили неотрицательные числа с обеих сторон неравенства, поэтому вправе возвести обе стороны в квадрат:
[begin{matrix} {{left( 2+sqrt{13} right)}^{2}}vee {{left( sqrt{21} right)}^{2}} \ 4+4sqrt{13}+13vee 21 \ 4sqrt{13}vee 3 \end{matrix}]
Думаю, тут и ежу понятно, что $4sqrt{13} gt 3$, поэтому $frac{-1+sqrt{13}}{2} gt frac{-3+sqrt{21}}{2}$, окончательно точки на осях будут расставлены вот так:
Случай некрасивых корней Напомню, мы решаем совокупность, поэтому в ответ пойдёт объединение, а не пересечение заштрихованных множеств.
Ответ: $xin left( -infty ;frac{-3+sqrt{21}}{2} right)bigcup left( frac{-1+sqrt{13}}{2};+infty right)$
Как видите, наша схема прекрасно работает как для простых задач, так и для весьма жёстких. Единственное «слабое место» в таком подходе — нужно грамотно сравнивать иррациональные числа (и поверьте: это не только корни). Но вопросам сравнения будет посвящён отдельный (и очень серьёзный урок). А мы идём дальше.
3. Неравенства с неотрицательными «хвостами»
Вот мы и добрались до самого интересного. Это неравенства вида:
[left| f right| gt left| g right|]
Вообще говоря, алгоритм, о котором мы сейчас поговорим, верен н только для модуля. Он работает во всех неравенствах, где слева и справа стоят гарантированно неотрицательные выражения:
[f gt g,quad fge 0,gge 0]
Что делать с этими задачами? Просто помните:
В неравенствах с неотрицательными «хвостами» можно возводить обе части в любую натуральную степень. Никаких дополнительных ограничений при этом не возникнет.
Прежде всего нас будет интересовать возведение в квадрат — он сжигает модули и корни:
[begin{align} & {{left( left| f right| right)}^{2}}={{f}^{2}}; \ & {{left( sqrt{f} right)}^{2}}=f. \end{align}]
Вот только не надо путать это с извлечением корня из квадрата:
[sqrt{{{f}^{2}}}=left| f right|ne f]
Бесчисленное множество ошибок было допущено в тот момент, когда ученик забывал ставить модуль! Но это совсем другая история (это как бы иррациональные уравнения), поэтому не будем сейчас в это углубляться. Давайте лучше решим парочку задач:
Задача. Решите неравенство:
[left| x+2 right|ge left| 1-2x right|]
Решение. Сразу заметим две вещи:
- Это нестрогое неравенство. Точки на числовой прямой будут выколоты.
- Обе стороны неравенства заведомо неотрицательны (это свойство модуля: $left| fleft( x right) right|ge 0$).
Следовательно, можем возвести обе части неравенства в квадрат, чтобы избавиться от модуля и решать задачу обычным методом интервалов:
[begin{align} & {{left( left| x+2 right| right)}^{2}}ge {{left( left| 1-2x right| right)}^{2}}; \ & {{left( x+2 right)}^{2}}ge {{left( 2x-1 right)}^{2}}. \end{align}]
На последнем шаге я слегка схитрил: поменял последовательность слагаемых, воспользовавшись чётностью модуля (по сути, умножил выражение $1-2x$ на −1).
Дальше можно перенести всё вправо и расписать разность квадратов. Только аккуратно:
[begin{align} & {{left( 2x-1 right)}^{2}}-{{left( x+2 right)}^{2}}le 0; \ & left( left( 2x-1 right)-left( x+2 right) right)cdot left( left( 2x-1 right)+left( x+2 right) right)le 0; \ & left( 2x-1-x-2 right)cdot left( 2x-1+x+2 right)le 0; \ & left( x-3 right)cdot left( 3x+1 right)le 0. \end{align}]
Решаем методом интервалов. Переходим от неравенства к уравнению:
[begin{align} & left( x-3 right)left( 3x+1 right)=0; \ & {{x}_{1}}=3;{{x}_{2}}=-frac{1}{3}. \end{align}]
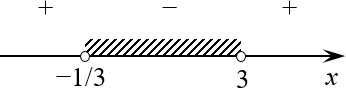
Отмечаем найденные корни на числовой прямой. Ещё раз: все точки закрашены, поскольку исходное неравенство — нестрогое!
Избавление от знака модуля Напомню для особо упоротых: знаки мы берём из последнего неравенства, которое было записано перед переходом к уравнению. И закрашиваем области, требуемые в том же неравенстве. В нашем случае это $left( x-3 right)left( 3x+1 right)le 0$.
Ну вот и всё. Задача решена.
Ответ: $xin left[ -frac{1}{3};3 right]$.
Задача. Решите неравенство:
[left| {{x}^{2}}+x+1 right|le left| {{x}^{2}}+3x+4 right|]
Решение. Делаем всё то же самое. Я не буду комментировать — просто посмотрите на последовательность действий.
Возводим в квадрат:
[begin{align} & {{left( left| {{x}^{2}}+x+1 right| right)}^{2}}le {{left( left| {{x}^{2}}+3x+4 right| right)}^{2}}; \ & {{left( {{x}^{2}}+x+1 right)}^{2}}le {{left( {{x}^{2}}+3x+4 right)}^{2}}; \ & {{left( {{x}^{2}}+x+1 right)}^{2}}-{{left( {{x}^{2}}+3x+4 right)}^{2}}le 0; \ & left( {{x}^{2}}+x+1-{{x}^{2}}-3x-4 right)times \ & times left( {{x}^{2}}+x+1+{{x}^{2}}+3x+4 right)le 0; \ & left( -2x-3 right)left( 2{{x}^{2}}+4x+5 right)le 0. \end{align}]
Метод интервалов:
[begin{align} & left( -2x-3 right)left( 2{{x}^{2}}+4x+5 right)=0 \ & -2x-3=0Rightarrow x=-1,5; \ & 2{{x}^{2}}+4x+5=0Rightarrow D=16-40 lt 0Rightarrow varnothing . \end{align}]
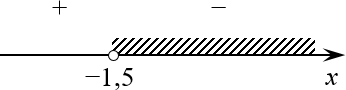
Всего один корень на числовой прямой:
Ответ — целый интервал Ответ: $xin left[ -1,5;+infty right)$.
Небольшое замечание насчёт последней задачи. Как точно подметил один мой ученик, оба подмодульных выражения в данном неравенстве заведомо положительны, поэтому знак модуля можно без ущерба для здоровья опустить.
Но это уже совсем другой уровень размышлений и другой подход — его условно можно назвать методом следствий. О нём — в отдельном уроке. А сейчас перейдём к финальной части сегодняшнего урока и рассмотрим универсальный алгоритм, который работает всегда. Даже тогда, когда все предыдущие подходы оказались бессильны.:)
4. Метод перебора вариантов
А что, если все эти приёмы не помогут? Если неравенство не сводится неотрицательным хвостам, если уединить модуль не получается, если вообще боль-печаль-тоска?
Тогда на сцену выходит «тяжёлая артиллерия» всей математики — метод перебора. Применительно к неравенствам с модулем выглядит он так:
- Выписать все подмодульные выражения и приравнять их к нулю;
- Решить полученные уравнения и отметить найденные корни на одной числовой прямой;
- Прямая разобьётся на несколько участков, внутри которого каждый модуль имеет фиксированный знак и потому однозначно раскрывается;
- Решить неравенство на каждом таком участке (можно отдельно рассмотреть корни-границы, полученные в пункте 2 — для надёжности). Результаты объединить — это и будет ответ.:)
Ну как? Слабо? Легко! Только долго. Посмотрим на практике:
Задача. Решите неравенство:
[left| x+2 right| lt left| x-1 right|+x-frac{3}{2}]
Решение. Эта хрень не сводится к неравенствам вида $left| f right| lt g$, $left| f right| gt g$ или $left| f right| lt left| g right|$, поэтому действуем напролом.
Выписываем подмодульные выражения, приравниваем их к нулю и находим корни:
[begin{align} & x+2=0Rightarrow x=-2; \ & x-1=0Rightarrow x=1. \end{align}]
Итого у нас два корня, которые разбивают числовую прямую на три участка, внутри которых каждый модуль раскрывается однозначно:
Разбиение числовой прямой нулями подмодульных функций Рассмотрим каждый участок отдельно.
1. Пусть $x lt -2$. Тогда оба подмодульных выражения отрицательны, и исходное неравенство перепишется так:
[begin{align} & -left( x+2 right) lt -left( x-1 right)+x-1,5 \ & -x-2 lt -x+1+x-1,5 \ & x gt 1,5 \end{align}]
Получили довольно простое ограничение. Пересечём его с исходным предположением, что $x lt -2$:
[left{ begin{align} & x lt -2 \ & x gt 1,5 \end{align} right.Rightarrow xin varnothing ]
Очевидно, что переменная $x$ не может одновременно быть меньше −2, но больше 1,5. Решений на этом участке нет.
1.1. Отдельно рассмотрим пограничный случай: $x=-2$. Просто подставим это число в исходное неравенство и проверим: выполняется ли оно?
[begin{align} & {{left. left| x+2 right| lt left| x-1 right|+x-1,5 right|}_{x=-2}} \ & 0 lt left| -3 right|-2-1,5; \ & 0 lt 3-3,5; \ & 0 lt -0,5Rightarrow varnothing . \end{align}]
Очевидно, что цепочка вычислений привела нас к неверному неравенству. Следовательно, исходное неравенство тоже неверно, и $x=-2$ не входит в ответ.
2. Пусть теперь $-2 lt x lt 1$. Левый модуль уже раскроется с «плюсом», но правый — всё ещё с «минусом». Имеем:
[begin{align} & x+2 lt -left( x-1 right)+x-1,5 \ & x+2 lt -x+1+x-1,5 \& x lt -2,5 \end{align}]
Снова пересекаем с исходным требованием:
[left{ begin{align} & x lt -2,5 \ & -2 lt x lt 1 \end{align} right.Rightarrow xin varnothing ]
И снова пустое множество решений, поскольку нет таких чисел, которые одновременно меньше −2,5, но больше −2.
2.1. И вновь частный случай: $x=1$. Подставляем в исходное неравенство:
[begin{align} & {{left. left| x+2 right| lt left| x-1 right|+x-1,5 right|}_{x=1}} \ & left| 3 right| lt left| 0 right|+1-1,5; \ & 3 lt -0,5; \ & 3 lt -0,5Rightarrow varnothing . \end{align}]
Аналогично предыдущему «частному случаю», число $x=1$ явно не входит в ответ.
3. Последний кусок прямой: $x gt 1$. Тут все модули раскрываются со знаком «плюс»:
[begin{align} & x+2 lt x-1+x-1,5 \ & x+2 lt x-1+x-1,5 \ & x gt 4,5 \end{align}]
И вновь пересекаем найденное множество с исходным ограничением:
[left{ begin{align} & x gt 4,5 \ & x gt 1 \end{align} right.Rightarrow xin left( 4,5;+infty right)]
Ну наконец-то! Мы нашли интервал, который и будет ответом.
Ответ: $xin left( 4,5;+infty right)$
Напоследок — одно замечание, которое, возможно, убережёт вас от глупых ошибок при решении реальных задач:
Решения неравенств с модулями обычно представляют собой сплошные множества на числовой прямой — интервалы и отрезки. Гораздо реже встречаются изолированные точки. И ещё реже случается так, что границ решения (конец отрезка) совпадает с границей рассматриваемого диапазона.
Следовательно, если границы (те самые «частные случаи») не входят в ответ, то почти наверняка не войдут в ответ и области слева-справа от этих границ. И напротив: граница вошла в ответ — значит, и какие-то области вокруг неё тоже будут ответами.
Помните об этом, когда проверяете свои решения.
Смотрите также:
- Неравенства с модулем: графическое решение
- Уравнения, содержащие несколько модулей, вложенных друг в друга: как их решать?
- Решение ЕГЭ-2011: вариант 1, часть B
- Сводный тест по задачам B15 (1 вариант)
- Учимся расщеплять ответы в тригонометрических уравнениях
- Задача C1: тригонометрия и показательная функция — 1 вариант
Не всегда верно, что
|a+b| = |a| + |b|
например
если a = 2 и b = -3, тогда a+b = -1 и поэтому |a+b| = |-1| = 1
в то время как
|a|+|b| = |2|+|-3| = 2+3 = 5 поэтому |a+b| = |a|+|b|
1.2.5 ТЕОРЕМА — (Неравенство треугольника)
Если a b тогда |a+b| ≤ |a|+|b|
Доказательство
Так как для любого действительного числа a и b, мы знаем, что
-|a| ≤ a ≤ |a| and -|b| ≤ b ≤ |b|
-|a| ≤ a ≤ |a|
+
-|b| ≤ b ≤ |b|
______________
= -|a| + -|b| ≤ a+b ≤ |a|+|b|
______________________________________________
Сейчай мы имеем два случая:
Разность модулей и модуль разности
Существуют следующие свойства модуля действительных чисел:
Проведем доказательства, рассматривая различные случаи значений a и b .
Доказательство 1) |a + b| ≤ |a| + |b|:
Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b . Из этого следует, что |a + b| = |a| + |b| .
Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a| . Выражение же |a| + |b| равно сумме абсолютных значений a и b , что больше, чем b – a . Поэтому |a + b| .
Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b| , что также меньше суммы модулей |a| + |b| .
Если a и b – отрицательные числа, то получим |–a – b| . Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b| ). Но уже было доказано, что |a + b| = |a| + |b| , следовательно и |–a – b| = |a| + |b| .
Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.
Доказательство 3) , a ≠ 0:
Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/ a .
Доказательство 4) |a – b| ≥ |a| – |b|:
Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b| , потому что можно не брать модули вообще и тогда с двух сторон получим a – b .
Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b| , что больше, чем |a| – |b| .
Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b| , что больше, чем |a| – |b| .
В этой статье мы детально разберем модуль числа. Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.
Навигация по странице.
Модуль числа – определение, обозначение и примеры
Сначала введем обозначение модуля числа. Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль целого числа −7 можно записать как ; модуль рационального числа 4,125 записывается как , а модуль иррационального числа имеет запись вида .
Так мы определились с обозначением, теперь пришло время дать определение модуля числа. Чтобы хорошо понять определение модуля числа необходимо хорошо владеть материалом статьи положительные и отрицательные числа, а также статьи противоположные числа.
Следующее определение модуля относится к действительным числам, а следовательно, и к натуральным числам, и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в последнем пункте этой статьи.
Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .
Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a .
Запись можно представить в более компактной форме . Эта запись означает, что , если ( a больше или равно 0 ), и , если a .
Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.
Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как — отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .
В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака, а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа. Так модуль числа и абсолютная величина числа – это одно и то же.
Модуль числа как расстояние
Геометрически модуль числа можно интерпретировать как расстояние. Приведем определение модуля числа через расстояние.
Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.
Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.
Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .
Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.
Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .
То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.
Определение модуля числа через арифметический квадратный корень
Иногда встречается определение модуля через арифметический квадратный корень.
Модуль числа a – это арифметический квадратный корень из квадрата числа a , то есть, .
Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .
Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .
Свойства модуля
Модулю присущ ряд характерных результатов — свойства модуля. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.
Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом. В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.
Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.
Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.
Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел, то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.
Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.
Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника. Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , — длине отрезка АС , а — длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .
Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .
Модуль комплексного числа
Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.
Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.
Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .
Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .
Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.
Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.
По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.
Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z , если оно записано в тригонометрической форме как или в показательной форме . Здесь . Например, модуль комплексного числа равен 5 , а модуль комплексного числа равен .
Можно также заметить, что произведение комплексного числа на комплексно сопряженное число дает сумму квадратов действительной и мнимой части. Действительно, . Полученное равенство позволяет дать еще одно определение модуля комплексного числа.
Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .
В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Модуль числа — это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности.
А между тем она проста как апельсин. Но чтобы ее понять, давай сначала разберемся зачем нужен модуль.
Вот смотри, ситуация первая.
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, неважно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая.
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией Lays, если они тебе недовесили?
Нет. Потому что Lays устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» — это и есть модуль.
Ситуация третья.
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч — это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от нуля в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления .
Итак, ты делаешь шага вперёд и оказываешься в точке с координатой .
Это означает, что ты удалился от места, где стоял на шага ( единичных отрезка). То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно .
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой сделать шага в обратную сторону, то окажешься в точке с координатой .
Какое расстояние было пройдено в первом и во втором случае? Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки ( и ), в которых ты оказался одинаково удалены от точки, из которой было начато движение ( ).
Таким образом, мы приблизились к понятию модуля . Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа будет . Модуль числа также равен , потому что расстояние не может быть отрицательным !
Модуль – это абсолютная величина
Обозначается модуль просто:
Итак, найдём модуль числа и :
Основные свойства модуля
Вот мы и приблизились к первому свойству модуля:
Модуль не может быть выражен отрицательным числом.
То есть, если – число положительное, то его модуль будет равен этому же числу:
если ext mathbf ,»> то .
Если – отрицательное число, то его модуль равен противоположному числу:
А если ? Ну, конечно! Его модуль также равен :
Из этого следует, что модули противоположных чисел равны, то есть:
А теперь потренируйся:
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда?
А если перед тобой вот такое число:
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим :
Если , то какой знак имеет ? Ну конечно, !
А, значит, знак модуля раскрываем, меняя знак у выражения:
Разобрался? Тогда попробуй сам:
Какими же ещё свойствами обладает модуль?
Если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
А что, если нам нужно разделить два числа (выражения) под знаком модуля?
Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
при условии, что (так как на ноль делить нельзя).
Стоит запомнить ещё одно свойство модуля:
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:
Почему так? Всё очень просто!
Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.
Рассмотрим на примере:
Выражения также равны, если оба числа отрицательны:
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.
Что если перед нами такое выражение:
Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что , а значит .
Число больше нуля, а значит можно просто записать:
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
А чему равно такое выражение:
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства. И что же получается? А вот что:
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
Ну, и почему сомнения? Действуем смело!
Во всем разобрался? Тогда вперед тренироваться на примерах!
1. Найдите значение выражения , если .
2. У каких чисел модуль равен ?
3. Найдите значение выражений:
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Итак, подставим значения и в выражение
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и .
Все уловил? Тогда пора перейти к более сложному!
Попробуем упростить выражение
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
Получается, значение первого выражения под модулем .
, следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Во втором случае просто отбросим знак модуля:
Упростим данное выражение целиком:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа — это само число , если , и число , если :
http://www.math10.com/ru/algebra/modul/absolutnie-znacheniya.html
http://planshet-info.ru/kompjutery/raznost-modulej-i-modul-raznosti
Задание. Найдите сумму всех
целых решений неравенства |x2-3x-13|>x2-3x-13
Варианты ответов:
1)
-9;
2)
9;
3)
0;
4)
-12;
5)
12.
Анализ
Обратим внимание, что
выражение под модулем и выражение в правой части – равные многочлены, поэтому
проанализируем, при каких a верно
неравенство |a|>a. Понятно, что нам
нужно рассмотреть случаи, когда a –
отрицательное, положительное и равное нулю. Подставляем любые значения a и
смотрим, верно ли неравенство:
При a=-1: |-1|>-1 – верно;
При a=0: |0|>0 – неверно.
При a=1: |1|>1 – неверно.
Решение
То есть, неравенство
верно, когда под модулем стоит отрицательное выражение, поэтому исходное
неравенство равносильно неравенству
x2-3x-13<0
– квадратное неравенство.
Рассмотрим функцию y= x2-3x-13.
График – парабола, ветви направлены вверх, нули: D=9+4∙13=61. Корни находим приблизительно:
x1=(3-7,8)/2=-2,2;
x2=(3+7,8)/2=5,4.
Строим схематично график:
Решение неравенства xϵ(-2,2; 5,4). Целые значения переменной
-2; -1; 0; 1; 2; 3; 4; 5. Сумма 3+4+5=12.
Ответ. 5
п.1. Понятие совокупности неравенств с одной переменной и его решения
Несколько неравенств с одной переменной образуют совокупность, если нужно найти такое множество значений переменной, которое будет решением хотя бы одного из неравенств.
Решением совокупности неравенств с одной переменной является такое множество значений этой переменной, которое превращает хотя бы одно из неравенств в верное числовое неравенство.
Следствие: общим решением совокупности неравенств с одной переменной является объединение частных решений каждого из неравенств системы.
Например: $ left[ begin{array}{ l l } mathrm{x^2 geq 0} & \ mathrm{x-4lt 1} & end{array}right. Leftrightarrow left[ begin{array}{ l l } mathrm{xleq-2cup x geq 2} & \ mathrm{xlt 5} & end{array}right. Leftrightarrow mathrm{x in mathbb{R}} $ — любое действительное число.
п.2. Алгоритм решения совокупности неравенств с одной переменной
Шаг 1. Найти множество решений для каждого из неравенств системы. Если какое-либо частное решение является пустым множеством, отбросить его, но продолжить решение.
Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных непустых частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать.
Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их объединение – это и будет общим решением системы.
Шаг 4. Работа завершена.
Например: $ left[ begin{array}{ l l } mathrm{x^2-1 lt 0} & \ mathrm{x+5geq8} & end{array}right. Leftrightarrow left[ begin{array}{ l l } mathrm{-1lt xlt 1} & \ mathrm{xgeq 3} & end{array}right. Leftrightarrow mathrm{-1lt x lt 1cup xgeq 3} $
или $mathrm{xin (-1;1)cupleft[3;+inftyright)}$
Подробней о сравнении систем и совокупностей неравенств, их соответствии логическим операциям, см. §39 справочника для 8 класса.
п.3. Решение неравенств с модулем
Пусть f(x) — некоторая функция от x, a – некоторое действительное число. Составим таблицу возможных неравенств с модулем и их решений:
a < 0
Решений нет, $mathrm{xinvarnothing}$
Выполняется всегда, $mathrm{xinmathbb{R}}$
a = 0
Решений нет, $mathrm{xinvarnothing}$
Решаем неравенство: $mathrm{f(x)ne 0}$
a > 0
Решаем двойное неравенство: $mathrm{-alt f(x)lt a}$
т.е. систему: $ left{ begin{array}{ l l } mathrm{f(x)gt -a} & \ mathrm{f(x)lt a} & end{array}right. $
Решаем совокупность: $ left[ begin{array}{ l l } mathrm{f(x)lt -a} & \ mathrm{f(x)gt a} & end{array}right. $
При решении неравенств с дробями и корнями не забывайте про ОДЗ – область допустимых значений для f(x).
Например: Решим неравенство |x2 — 3x| < 2.
Соответствующее двойное неравенство: -2 < x2 — 3x < 2
Система: begin{gather*} left{ begin{array}{ l l } mathrm{x^2-3xgt -2} & \ mathrm{x^2-3xlt 2} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{x^2-3x+2gt 0} & \ mathrm{x^2-3x-2lt 0} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{(x-1)(x-2)gt 0 }& \ mathrm{(x-x_1)(x-x_2)lt 0} & end{array}right.\ mathrm{D=3^2-4cdot(-2)=9+8=17, x_{1,2}=frac{3pmsqrt{17}}{2}} end{gather*}
Ответ: (mathrm{xinleft(frac{3-sqrt{17}}{2};1right)cupleft(2;frac{3+sqrt{17}}{2}right)})
Пусть f(x),g(x) — некоторые функции от x.
Составим таблицу возможных неравенств с модулем и их решений:
|f(x)| < g(x)
|f(x)| > g(x)
Решаем систему: $$ left{ begin{array}{ l l } mathrm{f(x)gt -g(x)} & \ mathrm{f(x)lt g(x)} & end{array}right. $$
Решаем совокупность: $$ left[begin{array}{ l l } mathrm{f(x)lt -g(x)} & \ mathrm{f(x)gt g(x)} & end{array}right. $$
|f(x)| < |g(x)|
|f(x)| > |g(x)|
Решаем неравенство: $mathrm{f^2(x)lt g^2(x)}$
Решаем неравенство: $mathrm{f^2(x)gt g^2(x)}$
Например: Решим неравенство |x2 + 3x + 2| > 2 — x.
Решаем совокупность:
begin{gather*} left[ begin{array}{ l l } mathrm{x^2+3x+2lt x-2} & \ mathrm{x^2+3x+2gt 2-x} & end{array}right.Rightarrow left[ begin{array}{ l l } mathrm{x^2+2x+4lt 0} & \ mathrm{x^2+4xgt 0} & end{array}right. end{gather*}
y = x2 + 2x + 4 > 0 — парабола с a > 0 и D < 0, т.е. все её точки лежат над осью OX. Значит, решение первого неравенства – пустое множество, (xinvarnothing).
Решаем второе неравенство: $$ mathrm{x(x+4) gt 0Rightarrow xlt -4cup xgt 0} $$ Ответ: (mathrm{xin(-infty;-4)cup(0;+infty)})
п.4. Примеры
Пример 1. Решите неравенства:
а) |x + 2| > 5
Решаем совокупность: begin{gather*} left[ begin{array}{ l l } mathrm{x+2gt-5} & \ mathrm{x+2gt 5} & end{array}right.Rightarrow left[ begin{array}{ l l } mathrm{xlt -7} & \ mathrm{xgt 3} & end{array}right.Rightarrow xlt -7cup xgt 3 end{gather*} Ответ: (mathrm{xin(-infty;-7)cup(3;+infty)})
б) |22 — 7x| ≤ 6
Решаем систему: begin{gather*} left{ begin{array}{ l l } mathrm{22-7xgeq -6} & \ mathrm{22-7xleq 6} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{-7xgeq -28} & \ mathrm{-7xleq -16} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{xleq 4} & \ mathrm{xgeq 2frac27} & end{array}right.Rightarrow 2frac27leq xleq 4 end{gather*} Ответ: (mathrm{xinleft[2frac27;4right]})
в) |x2 — 2x| ≥ 6
Решаем совокупность: begin{gather*} left[ begin{array}{ l l } mathrm{x^2-2xleq -6} & \ mathrm{x^2-2xgeq 6} & end{array}right.Rightarrow left[ begin{array}{ l l } mathrm{x^2-2x+6leq 0} & \ mathrm{x^2-2x-6geq 0} & end{array}right. end{gather*} Парабола y = x2 — 2x + 6 > 0 ветками вверх с a > 0, D < 0 — всегда положительна.
Решение первого неравенства (mathrm{xinvarnothing}).
Решаем второе неравенство: begin{gather*} mathrm{D = 2^2-4cdot (-6)=28, x_{1,2}=frac{2pm2sqrt{7}}{2}=1pmsqrt{7}}\ (x-x_1)(x-x_2)geq 0Rightarrow xleq x_1 cup xgeq x_2Rightarrow xleq 1-sqrt{7}cup xgeq 1+sqrt{7} end{gather*} Ответ: (mathrm{xinleft(-infty;1-sqrt{7}right]cupleft[1+sqrt{7};+inftyright}}).
г) |x2 + x — 1| < 1
Решаем систему: begin{gather*} left{ begin{array}{ l l } mathrm{x^2+x-1gt -1} & \ mathrm{x^2+x-1lt 1} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{x^2+xgt 0} & \ mathrm{x^2+x-2lt 0} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{x(x+1)gt 0} & \ mathrm{(x+2)(x-1)lt 0} & end{array}right. end{gather*}
Ответ: (mathrm{xin(-2;-1)cup(0;1)})
Пример 2. Найдите целые решения неравенства:
а) |x2 + 4x – 5| < x + 9
Решаем систему: begin{gather*} left{ begin{array}{ l l } mathrm{x^2+4x-5gt -x-9} & \ mathrm{x^2+4x-5lt x+9} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{x^2+5x+4gt 0} & \ mathrm{x^2+3x-14lt 0} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{(x+1)(x+4)gt 0} & \ mathrm{(x-x_1)(x-x_2)lt 0} & end{array}right.\ mathrm{D=3^2-4cdot(-14)=65, x_{1,2}=frac{-3pmsqrt{65}}{2}} end{gather*}
$$ mathrm{xinleft(frac{-3-sqrt{65}}{2};-4right)cupleft(-1;frac{-3+sqrt{65}}{2}right)}. $$
Целые решения, входящие в данные промежутки: {–5; 0; 1; 2}
Ответ: {–5; 0; 1; 2}.
б) |x2 – 5x + 4| ≤ x – 1
Решаем систему: begin{gather*} left{ begin{array}{ l l } mathrm{x^2-5x+4geq 1-x} & \ mathrm{x^2-5x+4leq x-1} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{x^2-4x+3geq 0} & \ mathrm{x^2-6x+5leq 0} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{(x+1)(x-3)geq 0} & \ mathrm{(x-1)(x-5)leq 0} & end{array}right. end{gather*}
(mathrm{xinleft{1right}cup[3;5]})
Целые решения: {1; 3; 4; 5}
Ответ: {1; 3; 4; 5}.
Пример 3*. Решите неравенство:
а) |x2 – 5x + 4| < |4x – 10|
Возводим в квадрат левую и правую части: begin{gather*} mathrm{(x^2-5x+4)^2lt (4x-10)^2}\ mathrm{(x^2-5x+4)^2-(4x-10)^2lt 0} \ mathrm{left((x^2-5x+4)+(4x-10)right)left((x^2-5x+4)-(4x-10)right)lt 0}\ mathrm{(x^2-x-6)(x^2-9x+14)lt 0}\ mathrm{(x-3)(x+2)(x-2)(x-7)lt 0} end{gather*}
Ответ: (mathrm{xin(-2;2)cup(3;7)}).
б) |x + 1| + |x – 5| ≥ 8
Решаем совокупность:
begin{gather*} mathrm{y(x)=|x+1|+|x-5|=} left[ begin{array}{ l l l} mathrm{-(x+1)-(x-5), xlt -1} & \ mathrm{x+1-(x-5), -1leq xleq 5} & \ mathrm{x+1+x-5, xgt 5} & end{array}right. = \ = left[ begin{array}{ l l l} mathrm{-2x+4, xlt -2 }& \ mathrm{6, -1leq xleq 5} & \ mathrm{2x-4, xgt 5} & end{array}right. end{gather*}
Зелёная ломаная пересекается и находится под прямой y = 8 при x ∈ [-2; 6].
Ответ: (mathrm{xin[-2;6]}).
в) x2 – 5|x – 2| – 4 < 0
Решаем совокупность неравенств:
begin{gather*} mathrm{x^2-4lt 5|x-2|}Rightarrow left[ begin{array}{ l l } mathrm{5(x-2)lt 4-x^2} & \ mathrm{5(x-2)gt x^2-4} & end{array}right. Rightarrow left[ begin{array}{ l l } mathrm{x^2+5x-14lt 0}& \ mathrm{x^2-5x+6lt 9} & end{array}right. Rightarrow \ Rightarrow left[ begin{array}{ l l } mathrm{(x+7)(x-2)lt 0}& \ mathrm{(x-2)(x-3)lt 0} & end{array}right. end{gather*}
Ответ: (mathrm{xin(-7;2)cup(2;3)}).
г) (mathrm{frac{x^2+11x+28}{|x+5|}}<0)
Знаменатель всегда положительный, на знак не влияет. Неравенство строгое. Получаем систему:
begin{gather*} left{ begin{array}{ l l } mathrm{x^2+11+28lt 0} & \ mathrm{xne -5} & end{array}right. Rightarrow left{ begin{array}{ l l } mathrm{(x+4)(x+7)lt 0}& \ mathrm{xne -5} & end{array}right. Rightarrow left{ begin{array}{ l l } mathrm{-4lt xlt -7}& \ mathrm{xne -5} & end{array}right.Rightarrow \ Rightarrow mathrm{-4lt xlt -5cup -5lt xlt -7} end{gather*}
Ответ: (mathrm{xin(-4;-5)cup(-5;-7)}).
д) (mathrm{frac{|x-3|}{x^2+8x+12}} ⩽ 0)
Числитель всегда положительный, на знак не влияет. Неравенство нестрогое. Получаем совокупность:
begin{gather*} left[ begin{array}{ l l } mathrm{x=3} & \ mathrm{x^2+8x+12gt 0} & end{array}right. Rightarrow left[ begin{array}{ l l } mathrm{x=3}& \ mathrm{(x+2)(x+6)gt 0} & end{array}right. Rightarrow left[ begin{array}{ l l } mathrm{x=3}& \ mathrm{-6lt xlt -2} & end{array}right.Rightarrow \ Rightarrow mathrm{-6lt xlt -2cup x=3} end{gather*}
Ответ: (mathrm{xin(-6;-2)cup{3}}).
e) (mathrm{frac{4}{|x+2|}ltfrac{3x+23}{5}})
Решаем систему:
begin{gather*} left{ begin{array}{ l l } mathrm{frac{4}{x+2}gt -frac{3x+23}{5}} & \ mathrm{frac{4}{x+2}ltfrac{3x+23}{5}} & end{array}right. Rightarrow left{ begin{array}{ l l } mathrm{frac{4}{x+2}+frac{3x+23}{5}gt 0}& \ mathrm{frac{4}{x+2}-frac{3x+23}{5}lt 0} & end{array}right. Rightarrow left{ begin{array}{ l l } mathrm{frac{20+(3x+23)(x+2)}{5(x+2)}}& \ mathrm{frac{20-(3x+23)(x+2)}{5(x+2)}} & end{array}right.Rightarrow \ Rightarrow left{ begin{array}{ l l } mathrm{frac{3x^2+29x+66}{5(x+2)}gt 0}& \ mathrm{frac{-3x^2-29x-26}{5(x+2)}lt 0} & end{array}right.Rightarrow left{ begin{array}{ l l } mathrm{frac{3x^2+29x+66}{x+2}gt 0}& \ mathrm{frac{3x^2+29x+26}{x+2}gt 0} & end{array}right. \ mathrm{D_1=29^2-4cdot 3cdot 66=49=7^2, x_{1,2}=frac{-29pm 7}{6}}=left[ begin{array}{ l l } mathrm{-6}& \ mathrm{-3frac23} & end{array}right. \ mathrm{D_2=29^2-4cdot 3cdot 26=529=23^2, x_{3,4}=frac{-29pm 23}{6}}=left[ begin{array}{ l l } mathrm{-8frac23}& \ mathrm{-1} & end{array}right. end{gather*}
Получаем:
begin{gather*} left{ begin{array}{ l l } mathrm{frac{(c+6)left(x+3frac23right)}{x+2}gt 0} & \ mathrm{frac{left(x+8frac23right)(x+1)}{x+2}gt 0} & end{array}right. end{gather*}
Ответ: (mathrm{xinleft(-6;-3frac23right)cup(-1;infty)}).
Модулем числа
называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа -6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х
|, |а
| и т.д.
(Подробнее — в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1
. Решить уравнение
|10
х
— 5| = 15.
Решение
.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
10х
— 5 = 15
10х
— 5 = -15
Решаем:
10х
= 15 + 5 = 20
10х
= -15 + 5 = -10
х
= 20: 10
х
= -10: 10
х
= 2
х
= -1
Ответ
: х
1 = 2, х
2 = -1.
Пример 2
. Решить уравнение
|2
х
+ 1| =
х
+ 2.
Решение
.
Поскольку модуль — число неотрицательное, то х
+ 2 ≥ 0. Соответственно:
х
≥ -2.
Составляем два уравнения:
2х
+ 1 = х
+ 2
2х
+ 1 = -(х
+ 2)
Решаем:
2х
+ 1 = х
+ 2
2х
+ 1 = —х
— 2
2х
— х
= 2 — 1
2х
+ х
= -2 — 1
х
= 1
х
= -1
Оба числа больше -2. Значит, оба являются корнями уравнения.
Ответ
: х
1 = -1, х
2 = 1.
Пример 3
. Решить уравнение
|х
+ 3| — 1
————— = 4
х
— 1
Решение
.
Уравнение имеет смысл, если знаменатель не равен нулю — значит, если х
≠ 1. Учтем это условие. Наше первое действие простое — не просто освобождаемся от дроби, а преобрахуем ее так, чтобы получить модуль в чистом виде:
|х
+ 3| — 1 = 4 · (х
— 1),
|х
+ 3| — 1 = 4х
— 4,
|х
+ 3| = 4х
— 4 + 1,
|х
+ 3| = 4х
— 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число — то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х
— 3 ≥ 0
4х
≥ 3
х
≥ 3/4
Таким образом, у нас появилось второе условие: корень уравнения должен быть не меньше 3/4.
В соответствии с правилом, составляем совокупность двух уравнений и решаем их:
х
+ 3 = 4х
— 3
х
+ 3 = -(4х
— 3)
х
+ 3 = 4х
— 3
х
+ 3 = -4х
+ 3
х
— 4х
= -3 — 3
х
+ 4х
= 3 — 3
х
= 2
х
= 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения не может быть равен 1, и он должен быть не меньше 3/4. То есть х
≠ 1, х
≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов — число 2. Значит, только оно и является корнем исходного уравнения.
Ответ
: х
= 2.
Неравенства с модулем.
Пример 1
. Решить неравенство
|
х
— 3|
Решение
.
Правило модуля гласит:
|а
| = а
, если а
≥ 0.
|а
| = —а
, если а
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая: х
— 3 ≥ 0 и х
— 3
1) При х
— 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х
— 3
2) При х
— 3
-(х
— 3)
Раскрыв скобки, получаем:
—х
+ 3
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
х
— 3 ≥ 0
х
— 3
х
— 3 —х
+ 3
Решим их:
х
≥ 3
х
х
х
> -1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х
х
Определяем наименьшее и наибольшее значения. Это -1 и 7. При этом х
больше -1, но меньше 7.
Кроме того, х
≥ 3. Значит, решением неравенства является все множество чисел от -1 до 7, исключая эти крайние числа.
Ответ
: -1 х
Или: х
∈ (-1; 7).
Дополнения
.
1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х
— 3| х
до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа — к точке 7. Таким образом, точки х
мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
1 х
2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:
4 х
— 3
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число -4 являются границами решения неравенства.
4 + 3 х
1 х
Пример 2
. Решить неравенство
|
х
— 2| ≥ 5
Решение
.
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны -3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ
: -3 ≥ х
≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
5 ≥ х
— 2 ≥ 5
5 + 2 ≥ х
≥ 5 + 2
Ответ тот же: -3 ≥ х
≥ 7.
Или: х
∈ [-3; 7]
Пример решен.
Пример 3
. Решить неравенство
6
х
2 — |
х
| — 2 ≤ 0
Решение
.
Число х
может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х
≥ 0 и х
х
≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х 2 — х
— 2 ≤ 0.
Теперь о втором случае: если х
6х
2 — (-х
) — 2 ≤ 0.
Раскрываем скобки:
6х
2 + х
— 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
6х
2 — х
— 2 ≤ 0
х
≥ 0
6х
2 + х
— 2 ≤ 0
х
Надо решить неравенства в системах — а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х
2 — х
— 2 = 0.
Как решается квадратное уравнение — см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х
1 = -1/2, х 2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от -1/2 до 2/3. Пишем объединение решений при х
≥ 0:
[-1/2; 2/3].
Теперь решим второе квадратное уравнение:
6х
2 + х
— 2 = 0.
Его корни:
х
1 = -2/3, х
2 = 1/2.
Вывод: при х
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от -2/3 до 2/3, включая и эти крайние числа.
Ответ
: -2/3 ≤ х
≤ 2/3.
Или: х
∈ [-2/3; 2/3].
Методы (правила) раскрытия неравенств с модулями заключаются в последовательном раскрытии модулей, при этом используют интервалы знакопостоянства подмодульных функций. В конечном варианте получают несколько неравенств из которых и находят интервалы или промежутки, которые удовлетворяют условию задачи.
Перейдем к решению распространенных на практике примеров.
Линейные неравенства с модулями
Под линейными понимаем уравнения, в которых переменная входит в уравнение линейно.
Пример 1.
Найти решение неравенства
Решение:
Из условия задачи следует, что модули превращаются в ноль при x=-1
и x=-2.
Эти точки разбивают числовую ось на интервалы
В каждом из этих интервалов решим заданное неравенство. Для этого прежде всего составляем графические рисунки областей знакопостоянства подмодульных функций. Их изображают в виде областей с знаками каждой из функций
или интервалов со знаками всех функций.
На первом интервале раскрываем модули
Умножаем обе части на минус единицу, при этом знак в неравенстве поменяется на противоположный. Если Вам до этого правила трудно привыкнуть, то можете перенести каждую из частей за знак, чтобы избавиться минуса. В конечном варианте Вы получите
Пересечением множества x>-3
с областью на которой решали уравнения будет интервал (-3;-2)
. Для тех кому легче искать решения графически можете рисовать пересечение этих областей
Общие пересечение областей и будет решением. При строгом неровности края не включают. При нестрогое проверяют подстановкой.
На втором интервале получим
Сечением будет интервал (-2;-5/3).
Графически решение будет иметь вид
На третьем интервале получим
Данное условие не дает решений на искомой областе.
Поскольку два найдены решения (-3;-2)
и (-2;-5/3)
граничат точкой x=-2
, то проверяем и ее.
Таким образом точка x=-2
является решением. Общее решение с учетом этого будет выглядеть (-3;5/3).
Пример 2.
Найти решение неравенства
|x-2|-|x-3|>=|x-4|
Решение:
Нулями подмодульных функций будут точки x=2, x=3, x=4
.
При значениях аргументов меньше этих точек подмодульные функции отрицательные, а при больших – положительные.
Точки разбивают действительную ось на четыре интервала. Раскрываем модули согласно интервалов знакопостоянства и решаем неравенства.
1) На первом интервале все подмодульные функции отрицательные, поэтому при раскрытии модулей меняем знак на противоположный.
Пересечением найденных значений x
с рассматриваемым интервалом будет множество точек
2) На промежутке между точками x=2
и x=3
первая подмодульная функция положительная, вторая и третья – отрицательные. Раскрывая модули, получим
неравенство, которое в пересечении с интервалом, на котором решаем, дает одно решение – x=3.
3) На промежутке между точками x=3
и x=4
первая и вторая подмодульные функции положительные, а третья – отрицательная. На основе этого получим
Это условие показывает, что целый промежуток
будет удовлетворять неравенство с модулями.
4) При значениях x>4
все функции знакоположительные. При раскрытии модулей их знак не меняем.
Найденное условие в пересечении с интервалом дает следующее множество решений
Поскольку неравенство решено на всех интервалах, то остается найти общее всех найденных значений x.
Решением будут два интервала
На этом пример решен.
Пример 3.
Найти решение неравенства
||x-1|-5|>3-2x
Решение:
Имеем неравенство с модулем от модуля. Такие неравенства раскрывают по мере вложенности модулей, начиная с тех, которые размещены глубже.
Подмодульная функция x-1
преобразуется в нуль в точке x=1
. При меньших значениях за 1 она отрицательная и положительная для x>1
. На основе этого раскрываем внутренний модуль и рассматриваем неравенство на каждом из интервалов.
Сначала рассмотрим интервал от минус бесконечности до единицы
Подмодульная функция равна нулю в точке x=-4
. При меньших значениях она знакоположительная, при больших – отрицательная. Раскроем модуль для x
В пересечении с областью, на которой рассматриваем получим множество решений
Следующим шагом раскрываем модуль на интервале (-4;1)
С учетом области раскрытия модуля получим интервал решений
ЗАПОМНИТЕ: если Вы получили в подобных неровностях с модулями два интервала, граничащих общей точкой, то, как правило, она также является решением.
Для этого стоит лишь провести проверку.
В данном случае подставляем точку x=-4.
Итак x=-4
является решением.
Раскроем внутренний модуль для x>1
Подмодульная функция отрицательная для x Раскрывая модуль получим
Данное условие в сечении с интервалом (1;6)
дает пустое множество решений.
Для x>6
получим неравенство
Также решая получили пустое множество.
Учитывая все выше изложенное, единственным решением неравенства с модулями будет следующий интервал.
Неравенства с модулями, содержащие квадратные уравнения
Пример 4.
Найти решение неравенства
|x^2+3x|>=2-x^2
Решение:
Подмодульная функция обращается в нуль в точках x=0, x=-3.
Простой подстановкой минус единицы
устанавливаем, что она меньше нуля на интервале (-3;0)
и положительная за его пределами.
Раскроем модуль в областях где подмодульная функция положительная
Осталось определить области, где квадратная функция положительная. Для этого определяем корни квадратного уравнения
Для удобства подставляем точку x=0,
которая принадлежит интервалу (-2;1/2).
Функция отрицательная в этом интервале, значит решением будут следующие множества x
Здесь скобками обозначены края областей с решениями, это сделано сознательно, учитывая следующее правило.
ЗАПОМНИТЕ: Если неравенство с модулями, или простое неравенство является строгим, то края найденных областей не являются решениями, если же неравенства нестроги ()то края являются решениями (обозначают квадратными скобками).
Это правило использует многие преподаватели: если задано строгое неравенство, а Вы при вычислениях запишете в решении квадратную скобку ([,])
– они автоматом посчитают это за неправильный ответ. Также при тестировании, если задано нестрогое неравенство с модулями, то среди решений ищите области с квадратными скобками.
На интервале (-3;0)
раскрывая модуль меняем знак функции на противоположный
Учитывая область раскрытия неравенства, решение будет иметь вид
Вместе с предыдущей областью это даст два полуинтервала
Пример 5.
Найти решение неравенства
9x^2-|x-3|>=9x-2
Решение:
Задано нестрогое неравенство, подмодульная функция которого равна нулю в точке x=3.
При меньших значениях она отрицательная, при больших – положительная. Раскрываем модуль на интервале x
Находим дискриминант уравнения
и корни
Подставляя точку ноль, выясняем, что на промежутке [-1/9;1]
квадратичная функция отрицательна, следовательно промежуток является решением. Далее раскрываем модуль при x>3
Математика
является символом мудрости науки
,
образцом научной строгости и простоты
,
эталоном совершенства и красоты в науке.
Российский философ, профессор А.В. Волошинов
Неравенства с модулем
Наиболее сложно решаемыми задачами школьной математики являются неравенства
,
содержащие переменные под знаком модуля. Для успешного решения таких неравенств необходимо хорошо знать свойства модуля и иметь навыки их использования.
Основные понятия и свойства
Модуль (абсолютная величина) действительного числа
обозначается
и определяется следующим образом:
К простым свойствам модуля относятся следующие соотношения:
И
.
Отметим
,
что последние два свойства справедливы для любой четной степени.
Кроме того
,
если
,
где
, то
и
Более сложные свойства модуля
,
которые можно эффективно использовать при решении уравнений и неравенств с модулями
,
формулируются посредством следующих теорем:
Теорема 1.
Для любых аналитических функций
и
справедливо неравенство
.
Теорема 2.
Равенство
равносильно неравенству
.
Теорема 3.
Равенство
равносильно неравенству
.
Наиболее распространенными в школьной математике неравенствами
,
содержащие неизвестные переменные под знаком модуля
,
являются неравенства вида
и
,
где
некоторая положительная константа.
Теорема 4.
Неравенство
равносильно двойному неравенству
,
а решение неравенства
сводится к решению совокупности неравенств
и
.
Данная теорема является частным случаем теорем 6 и 7.
Более сложными неравенствами
,
содержащие модуль, являются неравенства вида
,
и
.
Методы решения таких неравенств можно сформулировать посредством следующих трех теорем.
Теорема 5.
Неравенство
равносильно совокупности двух систем неравенств
И
(1)
Доказательство.
Так как
,
то
Отсюда вытекает справедливость (1).
Теорема 6.
Неравенство
равносильно системе неравенств
Доказательство.
Так как
,
то из неравенства
следует
,
что
. При таком условии неравенство
и при этом вторая система неравенств (1) окажется несовместной.
Теорема доказана.
Теорема 7.
Неравенство
равносильно совокупности одного неравенства и двух систем неравенств
И
(3)
Доказательство.
Поскольку
,
то неравенство
всегда выполняется
,
если
.
Пусть
,
тогда неравенство
будет равносильно неравенству
,
из которого вытекает совокупность двух неравенств
и
.
Теорема доказана.
Рассмотрим типовые примеры решения задач на тему «Неравенства
,
содержащие переменные под знаком модуля».
Решение неравенств с модулем
Наиболее простым методом решения неравенств с модулем является метод
,
основанный на раскрытии модулей. Этот метод является универсальным
,
однако в общем случае его применение может привести к весьма громоздким вычислениям. Поэтому учащиеся должны знать и другие (более эффективные) методы и приемы решения таких неравенств. В частности
,
необходимо иметь навыки применения теорем
,
приведенных в настоящей статье.
Пример 1.
Решить неравенство
. (4)
Решение.
Неравенство (4) будем решать «классическим» методом – методом раскрытия модулей. С этой целью разобьем числовую ось
точками
и
на интервалы и рассмотрим три случая.
1. Если
,
то
,
,
,
и неравенство (4) принимает вид
или
.
Так как здесь рассматривается случай , то является решением неравенства (4).
2. Если
,
то из неравенства (4) получаем
или
. Так как пересечение интервалов
и
является пустым
,
то на рассматриваемом интервале решений неравенства (4) нет.
3. Если
,
то неравенство (4) принимает вид
или
. Очевидно
,
что
также является решением неравенства (4).
Ответ:
,
.
Пример 2.
Решить неравенство
.
Решение.
Положим
,
что
. Так как
,
то заданное неравенство принимает вид
или
. Поскольку
,
то
и отсюда следует
или
.
Однако
,
поэтому
или
.
Пример 3.
Решить неравенство
. (5)
Решение.
Так как
,
то неравенство (5) равносильно неравенствам
или
. Отсюда
,
согласно теореме 4
,
имеем совокупность неравенств
и
.
Ответ:
,
.
Пример 4.
Решить неравенство
. (6)
Решение.
Обозначим . Тогда из неравенства (6) получаем неравенства , , или .
Отсюда
,
используя метод интервалов
,
получаем
. Так как
,
то здесь имеем систему неравенств
Решением первого неравенства системы (7) является объединение двух интервалов
и
,
а решением второго неравенства – двойное неравенство
. Отсюда следует
,
что решение системы неравенств (7) представляет собой объединение двух интервалов
и
.
Ответ:
,
Пример 5.
Решить неравенство
. (8)
Решение.
Преобразуем неравенство (8) следующим образом:
Или
.
Применяя метод интервалов
,
получаем решение неравенства (8).
Ответ:
.
Примечание. Если в условии теоремы 5 положить и , то получим .
Пример 6.
Решить неравенство
. (9)
Решение.
Из неравенства (9) следует
. Преобразуем неравенство (9) следующим образом:
Или
Так как , то или .
Ответ:
.
Пример 7.
Решить неравенство
. (10)
Решение.
Так как и , то или .
В этой связи
и неравенство (10) принимает вид
Или
. (11)
Отсюда следует, что или . Так как , то и из неравенства (11) вытекает или .
Ответ:
.
Примечание.
Если к левой части неравенства (10) применить теорему 1
,
то получим
. Отсюда и из неравенства (10) следует
,
что
или
. Так как
,
то неравенство (10) принимает вид
или
.
Пример 8.
Решить неравенство
. (12)
Решение.
Так как
,
то
и из неравенства (12) следует
или
. Однако
,
поэтому
или
.
Отсюда получаем
или
.
Ответ:
.
Пример 9.
Решить неравенство
. (13)
Решение.
Согласно теореме 7 решением неравенства (13) являются или .
Пусть теперь
. В таком случае
и неравенство (13) принимает вид
или
.
Если объединить интервалы
и
,
то получим решение неравенства (13) вида
.
Пример 10.
Решить неравенство
.
(14)
Решение.
Перепишем неравенство (14) в равносильном виде: . Если к левой части данного неравенства применить теорему 1, то получим неравенство .
Отсюда и из теоремы 1 следует
,
что неравенство (14) выполняется для любых значений
.
Ответ:
любое число.
Пример 11.
Решить неравенство
. (15)
Решение.
Применяя теорему 1 к левой части неравенства (15)
,
получаем
. Отсюда и из неравенства (15) вытекает уравнение
,
которое имеет вид
.
Согласно теореме 3
,
уравнение
равносильно неравенству
. Отсюда получаем
.
Пример 12.
Решить неравенство
. (16)
Решение
. Из неравенства (16), согласно теореме 4, получаем систему неравенств
При решении неравенства
воспользуемся теоремой 6 и получим систему неравенств
из которой следует
.
Рассмотрим неравенство
. Согласно теореме 7
,
получаем совокупность неравенств
и
.
Второе неравенство совокупности справедливо для любого действительного
.
Следовательно
,
решением неравенства (16) являются
.
Пример 13.
Решить неравенство
. (17)
Решение.
Согласно теореме 1 можно записать
(18)
Принимая во внимание неравенство (17), делаем вывод о том, что оба неравенства (18) обращаются в равенства, т.е. имеет место система уравнений
По теореме 3 данная система уравнений равносильна системе неравенств
или
Пример 14.
Решить неравенство
. (19)
Решение.
Так как , то . Умножим обе части неравенства (19) на выражение , которое для любых значений принимает только положительные значения. Тогда получим неравенство, которое равносильно неравенству (19), вида
Отсюда получаем
или
,
где
. Так как
и
,
то решением неравенства (19) являются
и
.
Ответ:
,
.
Для более глубокого изучения методов решения неравенств с модулем можно посоветовать обратиться к учебным пособиям
,
приведенных в списке рекомендованной литературы.
1. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование
,
2013. – 608 с.
2. Супрун В.П. Математика для старшеклассников: методы решения и доказательства неравенств. – М.: Ленанд / URSS
,
2018. – 264 с.
3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS
,
2017. – 296 с.
Остались вопросы?
Чтобы получить помощь репетитора – зарегистрируйтесь .
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.