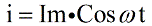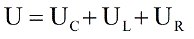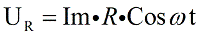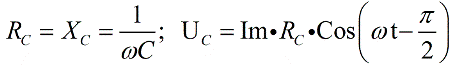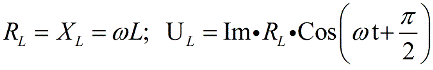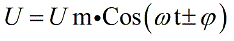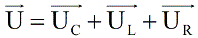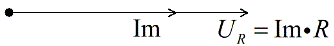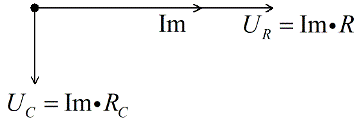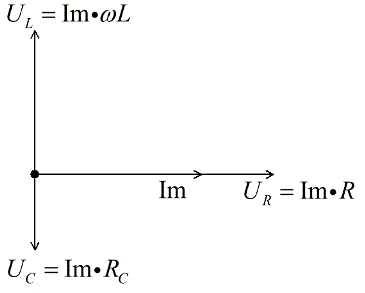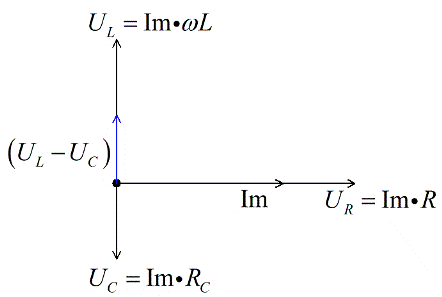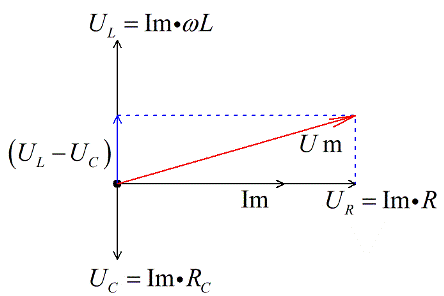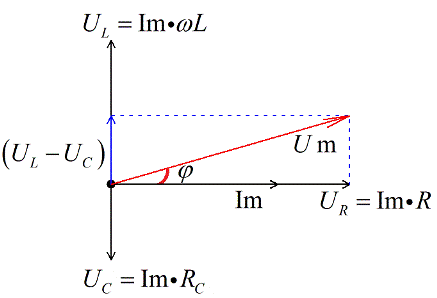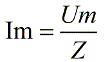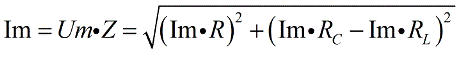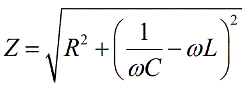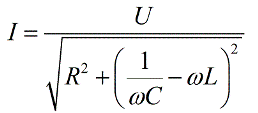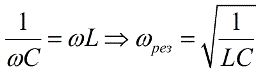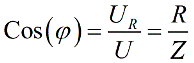Как построить векторную диаграмму токов и напряжений
Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.
В основе метода лежит тот факт, что всякую величину, меняющуюся по синусоидальному закону (смотрите — синусоидальные колебания), можно определить как проекцию на какое-то выбранное направление вектора, вращающегося вокруг своей начальной точки с угловой скоростью, равной угловой частоте колебаний изображаемой переменной величины.
Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.
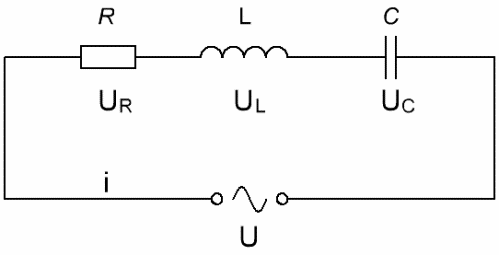
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:
Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR– на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:
Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:
А вот конденсатор в цепи переменного тока обладает реактивным емкостным сопротивлением, и напряжение на конденсаторе все время отстает по фазе от тока на Пи /2 , значит пишем:
Катушка, обладающая индуктивностью, в цепи переменного тока выступает реактивным индуктивным сопротивлением, и напряжение на катушке в любой момент времени опережает по фазе ток на Пи/ 2 , следовательно, для катушки запишем:
Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:
Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.
Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:
Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.
Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:
Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.
Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.
Напряжение на катушке опережает на Пи /2 ток, следовательно откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.
Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.
Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.
Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.
Запишем закон Ома для общего сопротивления Z (импеданса):
Из векторных изображений по Теореме Пифагора можем записать:
После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:
Тогда получим выражение для закона Ома для цепи переменного тока:
Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:
Косинус фи из наших геометрических построений получается:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.
Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.
Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
- Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
- Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.
Векторную диаграмму токов можно построить 2 разными способами:
- Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
- Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.
Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
- Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
- Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
- Напряжение резистора UR 10 вольт, его направление совпадает с током I.
- Сила тока в цепи I равняется 3 ампера.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
- Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
- Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
- Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
- Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
- Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
- Резистора UR;
- Конденсатора UC;
- Катушки UL.
- На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
- От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
- От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.
Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
- Показать результат сложения вектора UL и UC.
- При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
- Кроме того можно определить угол сдвига фазы φ в цепи.
Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
- На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
- Угловая величина обозначается как W.
- Также присутствует сам вектор Im и угол сдвига фаз φ.
- На плоскости выбрать точку отсчета.
- От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
- Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.
Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео по теме
Источник
Сегодня мы с вами должны будем опытным путём проверить
одну из закономерностей последовательного соединения проводников: правило
сложения напряжений.
Для выполнения этой работы мы воспользуемся оборудованием из
третьего комплекта в составе: источник тока, двухпредельный
вольтметр и амперметр, ключ, соединительные провода и резисторы, обозначенные R1 и R2. Ещё в
оборудовании вам может попасться реостат. Если так, то его тоже надо будет
использовать, хотя он и не будет влиять на итоговый результат. Но об этом ниже.
Прежде, чем
приступить к работе давайте с вами вспомним, что последовательное соединение
— это такое соединение, при котором проводники (потребители) имеют по одной
общей точке.
Опытным путём было установлено, что при последовательном
соединении сила тока во всех проводниках одинакова.
А вот полное
напряжение в цепи, или
напряжение на полюсах источника тока, равно сумме напряжений на отдельных
участках цепи:
Именно
последнюю зависимость нам с вами и предстоит сегодня проверить.
Итак, приступим. Первое, что мы с вами сделаем, — это
нарисуем схему, так как прежде чем собирать цепь мы должны заранее себе
представить, что мы будем собирать. Сначала мы нарисуем два резистора,
соединённых последовательно друг с другом. Отметим точки-узлы
к которым будем подключать вольтметр. Теперь между точками А и В параллельно первому резистору мы присоединяем
вольтметр, который обозначим через V1. А между точками В и С —
вольтметр V2.
И нарисуем ещё один вольтметр, который мы обозначим буквой V, подключённым между точками А
и С. Так мы с вами показываем проверяющим, как мы будем измерять
напряжение на концах каждого из резисторов и на двух резисторах одновременно.
Далее мы с вами нарисуем ключ и источник тока. Теперь
смотрите: если в условии задания речь о реостате не идёт, то мы просто замыкаем
нашу цепь; если же в условии реостат есть, то мы должны на схеме показать и
его, и затем обязательно включить его в цепь. Мы предположим, что реостат у нас
есть, так как убрать элемент из цепи всегда легче, чем его потом добавить.
Итак, теперь соберём экспериментальную установку. Для этого
подключаем последовательно друг к другу: источник тока, ключ (в разомкнутом
состоянии), два резистора, и реостат. При этом смотрите, реостат мы подключил и
больше его не трогаем — оставляем как есть, чтобы в дальнейшем он не смог
повлиять на результаты эксперимента. Параллельно резистору, обозначенному «Эр»
один» подключим вольтметр с пределом измерения 6 В.
Теперь запишем формулу, которой будем пользоваться при
выполнении данной работы. Как мы уже вспоминали, полное напряжение в цепи, или
напряжение на полюсах источника тока, равно сумме напряжений на отдельных
участках цепи:
Прежде чем приступить непосредственно к работе ещё раз
внимательно проверьте вашу электрическую цепь. Особое внимание обратите на
соблюдение полярности подключения вольтметра. Если всё в порядке, то включаем
источник питания и замыкаем ключ.
Смотрим на вольтметр: он показывает, что напряжение на концах
резистора R1
примерно равно 1,4 В. Размыкаем цепь и записываем значение напряжения с учётом
погрешности измерения:
Теперь мы должны подключить наш вольтметр параллельно второму
резистору.
Замыкаем ключ и видим, что напряжения на концах второго
проводника оказывается равным примерно 1,8 В. Размыкаем цепь и записываем это
значение напряжения с учётом погрешности:
И наконец, подключим вольтметр одновременно к двум
резисторам.
После замыкания ключа вольтметр нам показывает напряжение 3,4
В. Размыкаем цепь, отключаем источник питания и записываем последнее значение
напряжения в бланк ответов:
Теперь мы с вами должны найти сумму напряжений и сравнить её
с напряжением на концах обоих резисторов. Но если мы с вами их просто сложим
(1,4 В + 1,8 В = 3,2 В < 3,4 В), то окажется, что
закономерность напряжений последовательного соединения как бы нарушится.
Вот для таких случаев нам и дана погрешность измерений.
Поэтому мы должны сложить не только значения напряжений, но и
погрешности:
Таким образом получается, что с учётом погрешности измерений
сумма напряжений на концах обоих резисторов находится в интервале от 2,8 В до 3,6 В. Значение общего напряжения в цепи (3,4 В)
попадает в этот интервал значений.
Значит вывод мы можем написать так: при
последовательном соединении резисторов общее падение напряжения в цепи равно
сумме падений напряжений на отдельных участках цепи.
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:
Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Прикольный набор радиолюбителя по ссылке <<<
Похожие статьи по теме «последовательное и параллельное соединение»
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Загрузить PDF
Загрузить PDF
Если вам необходимо найти напряжение на сопротивлении (резисторе), первым делом необходимо определить тип электрической цепи. Для лучшего понимания основных терминов, используемых в физике и электротехнике, начните с первого раздела. Если же вы знакомы с терминологией, пропустите его и перейдите к описанию типа электрической цепи.
-
1
Рассмотрим понятие электрического тока. Воспользуемся аналогией: представьте, что вы поместили несколько зерен кукурузы в воду, текущую по трубе. Поток эквивалентен электрическому току, а зерна служат аналогией электронов.[1]
Говоря о потоке, мы описываем его количеством зерен, пересекших поперечное сечение трубы за одну секунду. При рассмотрении электрического тока мы измеряем его в амперах, соответствующих определенному (очень большому) количеству электронов, пересекающих сечение провода за одну секунду. -
2
Рассмотрим понятие электрического заряда. Каждый электрон имеет «отрицательный» электрический заряд. Это означает, что электроны притягиваются, или движутся по направлению к положительному заряду и отталкиваются, или движутся от отрицательного заряда. Каждый электрон обладает отрицательным зарядом, поэтому они отталкиваются друг от друга, стремясь разойтись в стороны.
-
3
Ознакомьтесь с понятием напряжения. Напряжение между двумя точками соответствует разности электрических зарядов, размещенных в этих точках. Чем больше эта разница, тем сильнее данные точки притягиваются друг к другу. Рассмотрим понятие напряжения на примере обычной электрической батарейки:
- Внутри батарейки происходят химические реакции, в результате которых образуются свободные электроны. Эти электроны движутся к отрицательному полюсу батарейки, удаляясь от ее положительного полюса (эти полюса соответствуют отрицательной и положительной клеммам батарейки). Чем дольше длится данный процесс, тем большее напряжение возникает между полюсами.
- Если вы соедините проволокой отрицательный и положительный полюса, у скопившихся электронов появится возможность покинуть отрицательный полюс. Они начнут перетекать к положительному полюсу, создавая электрический ток. Чем выше напряжение, тем больше электронов переместится к положительному полюсу за единицу времени.
-
4
Рассмотрим понятие электрического сопротивления. Его название точно отображает смысл. Чем выше сопротивление какого-либо объекта, тем тяжелее электронам пройти через него. В результате уменьшается ток, поскольку за единицу времени через проводник проходит меньшее число электронов.
- Сопротивлением, или резистором называется что-либо, увеличивающее сопротивление электрической цепи. «Резистор» можно приобрести в магазине электротоваров, но в цепи его роль может выполнять и любой другой объект, обладающий сопротивлением, например, лампа накаливания.
-
5
Запомните закон Ома. Он представляет собой простое соотношение между током, напряжением и сопротивлением. Запишите или запомните это соотношение — оно пригодится вам при расчете электрических цепей:
- Ток равен напряжению, поделенному на сопротивление
- Это записывается следующим образом: I = V / R
- Подумайте о том, что происходит, если вы увеличиваете V (напряжение) или R (сопротивление). Соответствует ли это приведенным выше объяснениям?
Реклама
-
1
Ознакомьтесь с понятием последовательного соединения. Такое соединение легко определить — оно представляет собой набор расположенных в ряд сопротивлений. Ток течет по этим сопротивлениям, последовательно проходя через каждое из них.
- Величина тока одинакова в любой точке цепи.[2]
- При расчете напряжения неважно, где именно в цепи расположен тот или иной резистор. Можно поменять их местами, напряжение на каждом из них останется неизменным.
- В качестве примера рассмотрим цепь, состоящую из трех последовательно соединенных сопротивлений: R1, R2 и R3. Пусть цепь питается от 12-вольтовой батарейки. Найдем напряжение на каждом сопротивлении.
- Величина тока одинакова в любой точке цепи.[2]
-
2
Сначала рассчитаем общее сопротивление. Сложим все сопротивления, включенные в цепь. В результате получим общее сопротивление резисторов, соединенных последовательно.
- Пусть три резистора R1, R2 и R3 имеют сопротивления 2 Ома, 3 Ома и 5 Ом соответственно. Тогда общее сопротивление составит 2 + 3 + 5 = 10 Ом.
-
3
Найдем ток. Используем закон Ома для всей цепи. Как мы помним, при последовательном соединении ток одинаков в любой точке цепи. Поэтому достаточно один раз определить ток и использовать найденную величину во всех последующих расчетах.
- Согласно закону Ома, I = V / R. Напряжение в цепи составляет 12 вольт, а общее сопротивление – 10 Ом. Отсюда находим I = 12 / 10 = 1,2 ампера.
-
4
Применим закон Ома, чтобы найти напряжение на резисторах. При помощи простых преобразований можно выразить напряжение через ток и сопротивление, переписав закон Ома следующим образом:
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-
5
Рассчитаем напряжение на каждом резисторе. Нам известны их сопротивления, протекающий через них ток, и в нашем распоряжении есть равенство, связывающее ток и сопротивление с напряжением. Подставляя в это равенство численные значения, находим ответ. Для нашего примера это выглядит следующим образом:
- Напряжение на резисторе R1 = V1 = (1,2A)(2Ома) = 2,4 вольта.
- Напряжение на резисторе R2 = V2 = (1,2A)(3Ома) = 3,6 вольта.
- Напряжение на резисторе R3 = V3 = (1,2A)(5Ом) = 6,0 вольт.
-
6
Проверим полученный ответ. При последовательном соединении сумма напряжений на каждом сопротивлении должна равняться общему напряжению в цепи.[3]
Сложите найденные напряжения, проверив, равна ли их сумма полному напряжению. Если нет, проверьте решение и найдите ошибку.- В нашем примере 2,4 + 3,6 + 6,0 = 12 вольт, что соответствует общему напряжению в цепи.
- Если ответ немного не совпадает с точным значением (например, 11,97 вместо 12), это, вероятно, вызвано тем, что вы на каком-то этапе округлили полученные величины. В этом случае ответ верен.
- Помните о том, что напряжение соответствует разности зарядов или количества электронов. Представьте себе, что вы подсчитываете число электронов, продвигаясь вдоль цепи. Если вы правильно сосчитаете их, то в результате получите разность зарядов между начальной и конечной точками цепи.
Реклама
-
1
Ознакомьтесь с понятием параллельного соединения. Представьте себе, что вы подсоединили провод к одному полюсу батарейки и расщепили его вдоль на две половины. Эти две части провода идут параллельно друг другу и затем вновь соединяются в один провод перед вторым полюсом батарейки. Если разместить на обеих ветках провода по резистору, они будут соединены «параллельно».[4]
- Параллельно можно соединить любое количество сопротивлений. Данное описание годится и для цепи, состоящей из сотни параллельных проводов.
-
2
Рассмотрим, как течет ток. При параллельном соединении он проходит через все ветки цепи. Ток будет течь через левый провод, пересекая расположенный на нем резистор; одновременно ток будет проходить и через правый провод с резистором. Пройдя через обе ветки, ток достигнет положительного полюса; ни на каком участке цепи ток не будет течь в обратном направлении.
-
3
Зная общее напряжение, найдем напряжение на каждом резисторе. Сделать это очень просто, если известно общее напряжение в цепи. При параллельном соединении напряжение на каждой ветке будет равно общему напряжению в цепи.[5]
Предположим, что наша цепь состоит из двух параллельно соединенных сопротивлений и питается 6-вольтовой батарейкой. В этом случае напряжение и на левом, и на правом сопротивлении составит 6 вольт. При этом каждая ветка может содержать любое число резисторов. Чтобы понять это, вернемся к последовательному соединению, рассмотренному выше:- Как мы помним, при последовательном соединении общее напряжение представляет собой сумму напряжений на каждом сопротивлении.
- Будем считать, что каждая ветка цепи представляет собой набор резисторов, соединенных последовательно. Таким образом, вычислив сумму напряжений на всех сопротивлениях одной из веток, мы найдем общее напряжение.
- Поскольку в нашем случае ток, текущий по каждой ветке, проходит через один резистор, напряжение на этом резисторе и будет общим напряжением в цепи.
-
4
Найдем общий ток в цепи. Если в условии задачи не указано общее напряжение, понадобятся некоторые дополнительные вычисления. Начнем с нахождения общего тока, протекающего по цепи. При параллельном соединении общий ток равен сумме токов, проходящих через каждую ветку цепи.[6]
- В математической записи это означает: Iобщий = I1 + I2 + I3…
- Для лучшего понимания представьте себе водопроводную трубу, разделенную на два рукава. Общее количество воды равно сумме воды, протекающей по каждому рукаву.
-
5
Найдем общее сопротивление цепи. При параллельном соединении резисторы не так сильно снижают ток через цепь, поскольку каждый из них вносит вклад в сопротивление лишь своей ветки цепи. Фактически чем больше ответвлений цепи, тем легче току пройти через нее. Чтобы найти общее сопротивление, необходимо решить относительно Rобщее следующее уравнение:
- 1 / Rобщее = 1 / R1 + 1 / R2 + 1 / R3 …
- Предположим, что цепь состоит из двух резисторов сопротивлением 2 Ома и 4 Ома, соединенных параллельно. Тогда 1 / Rобщее = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rобщее → Rобщее = 1/(3/4) = 4/3 = ~1,33 Ома.
-
6
Вычислим напряжение. Как мы помним, общее напряжение в цепи равно напряжению на одной из ее веток. Воспользуемся законом Ома. Рассмотрим конкретный случай:
- Через цепь течет ток силой 5 ампер. Общее сопротивление цепи равно 1,33 Ома.
- Согласно закону Ома, I = V / R, откуда V = IR
- V = (5A)(1,33Ом) = 6,65 вольт.
Реклама
Советы
- Если вы имеете дело со сложной цепью, состоящей из последовательно и параллельно соединенных сопротивлений, рассмотрите сначала два соседних резистора. Найдите их общее сопротивление, пользуясь правилами для последовательного или параллельного соединения, в соответствии с тем, как соединены данные резисторы. После этого можно рассматривать два данных резистора как одно сопротивление. Продолжайте таким образом объединять резисторы до тех пор, пока у вас не получится простая цепь, состоящая из параллельно либо последовательно соединенных сопротивлений.[7]
- Напряжение на сопротивлении часто называют «падением напряжения».
- Усвойте терминологию:
- Цепь — набор элементов (например, резисторов, конденсаторов и катушек), соединенных проводами так, что через них может проходить электрический ток.
- Резисторы — элементы, оказывающие сопротивление протекающему через них току и понижающие его силу
- Ток — поток электрического заряда через проволоку и элементы цепи, измеряется в амперах (А)
- Напряжение — работа, затрачиваемая на перемещение единичного заряда, измеряется в вольтах (В)
- Сопротивление — мера сопротивления прохождению электрического тока, измеряется в омах (Ом)
Реклама
Об этой статье
Эту страницу просматривали 167 510 раз.
Была ли эта статья полезной?
Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.
Содержание статьи
- 1 Как звучит закон Ома для участка цепи
- 2 Разбираемся что такое ток и сопротивление
- 3 Говорим о напряжении
- 4 Что изменится для полной цепи
- 5 Как найти сопротивление, напряжение
- 6 Параллельное и последовательное соединение
- 6.1 Последовательное соединение
- 6.2 Параллельное соединение
- 6.3 Что нам дает параллельное и последовательное соединение?
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.
Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Разбираемся что такое ток и сопротивление
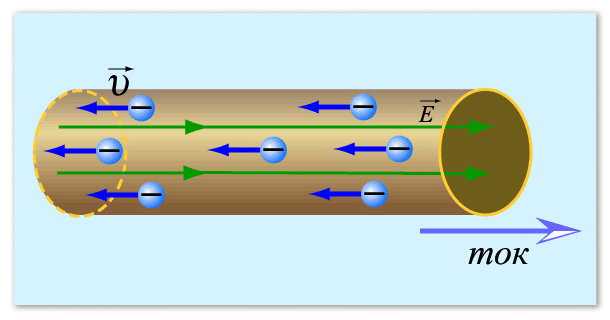
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.
Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.
Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
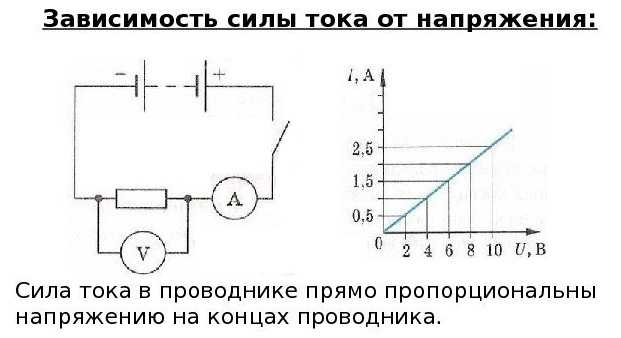
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.
Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.
Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.
Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.