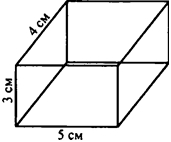
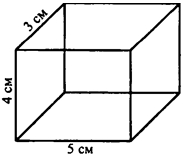
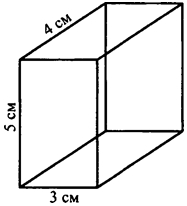
Как найти сумму площадей боковых граней параллелепипеда - Исправление недочетов и поиск решений вместе с Examum.ru

Ребра прямоугольного параллелепипеда равны 3 см, 4 см и 5 см.
а) Найдите площадь его основания и площадь боковой поверхности, то есть сумму площадей боковых граней.
б) Найдите площадь полной поверхности прямоугольного параллелепипеда.
Объясните, почему в задании «а» могут получиться три разных ответа.

reshalka.com

Математика 5 класс Никольский. Номер №506

Решение

Три разных ответа возможны из−за трех способов построения прямоугольного параллелепипеда.
Решение 1.

1) 5 * 4 = 20

(

)

− площадь основания;
2) 3 * 4 = 12

(

)

− площадь первой грани;
3) 3 * 5 = 15

(

)

− площадь второй грани;
4) (12 + 15) * 2 = 54

(

)

− площадь боковой поверхности.
Ответ:
20

− площадь основания;
54

(

)

− площадь боковой поверхности.

Решение 2.

1) 5 * 3 = 15

(

)

− площадь основания;
2) 3 * 4 = 12

(

)

− площадь первой грани;
3) 4 * 5 = 20

(

)

− площадь второй грани;
4) (12 + 20) * 2 = 64

(

)

− площадь боковой поверхности.
Ответ:
15

− площадь основания;
64

(

)

− площадь боковой поверхности.

Решение 3.

1) 3 * 4 = 12

(

)

− площадь основания;
2) 5 * 4 = 20

(

)

− площадь первой грани;
3) 3 * 5 = 15

(

)

− площадь второй грани;
4) (20 + 15) * 2 = 70

(

)

− площадь боковой поверхности.
Ответ:
12

− площадь основания;
70

(

)

− площадь боковой поверхности.

Источник

Напомним,
что призма, в основании которой лежит параллелограмм, называется параллелепипедом.

Стороны
параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами
параллелепипеда. Две грани параллелепипеда называются противолежащими,
если они не имеют общего ребра.

Например,
грани и
–
противолежащие.

Грани,
имеющие общее ребро, называются смежными. Например, грани и
–
смежные, ребро у
них общее.

Иногда
какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями,
тогда остальные грани – боковыми гранями, а их стороны, соединяющие
вершины оснований параллелепипеда, – его боковыми рёбрами.

В
нашем случае у параллелепипеда грани
и
–
его основания. Остальные же грани являются боковыми гранями.

Две
вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий, противолежащие вершины, называется диагональю
параллелепипеда. У параллелепипеда всего четыре диагонали.

Объединение
боковых граней называется боковой поверхностью параллелепипеда, а
объединение всех граней называется полной поверхностью параллелепипеда.
Тогда площадью боковой поверхности параллелепипеда называется сумма
площадей его боковых граней.

А
площадью полной поверхности параллелепипеда называется сумма площадей
всех его граней.

Параллелепипед
обладает следующими свойствами:

1.
Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.

2.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.

3.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его
измерений.

Объём
параллелепипеда равен произведению площади основания на
высоту.

Объём
прямоугольного параллелепипеда равен произведению трёх
его измерений.

Куб
– это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани
которого – равные квадраты.

Диагональ
куба с ребром равна
.

Объём
куба
равен ,
где –
ребро куба.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. В основании прямого параллелепипеда лежит параллелограмм
с основаниями см
и см
и острым углом .
Боковое ребро параллелепипеда равно см.
Найдите площадь полной поверхности параллелепипеда.

Решение.

Задача
вторая. Все грани параллелепипеда – ромбы с диагоналями см
и см.
Найдите площадь полной поверхности параллелепипеда.

Решение.

Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой см

со сторонами основания см
и см
и углом между ними .

Решение.

Задача
четвёртая. В прямоугольном параллелепипеде ребро
см,
см.
Найдите расстояние между диагональю параллелепипеда и
ребром .

Решение.

Задача
пятая. Две стороны основания параллелепипеда равны см
и см,
угол между ними .
Боковое ребро равно см
и наклонено к основанию под углом .
Найдите объём параллелепипеда.

Решение.

Задача
шестая. Все грани параллелепипеда – ромбы с периметром
равным и
острым углом .
Найдите объём параллелепипеда.
В ответ запишите значение .

Решение.

Источник

а) Возможны три случая.
I случай

S_осн = 5 ∙ 4 = 20 (см²) — площадь основания
S₁ = 3 ∙ 4 = 12 (см²) — площадь левой и правой боковых граней
S₂= 3 ∙ 5 = 15 (см²) — площадь передней и задней боковых граней
S_{бок.пов.} = 2 ∙ (S₁ + S₂) = 2 ∙ (15 + 12) = 2 ∙ 27 = 54 (см²) — площадь боковой поверхности

II случай

Sосн = 5 ∙ 3 = 15 (см²) — площадь основания
S₁ = 4 ∙ 3 = 12 (см²) — площадь левой и правой боковых граней
S₂ = 5 ∙ 4 = 20 (см²) — площадь передней и задней боковых граней
S_{бок.пов.} = 2 ∙ (S₁ + S₂) = 2 ∙ (12 + 20) = 2 ∙ 32 = 64 (см²) — площадь боковой поверхности

III случай

Sосн = 3∙4=12 (см²) — площадь оснований
S₁ = 5 ∙ 4 = 20 (см²) — площадь левой и правой боковых граней
S₂ = 5 ∙ 3 = 15 (см²) — площадь передней и задней боковых граней
S_{бок.пов.} = 2 ∙ (S₁ + S₂) = 2 ∙ (20 + 15) = 2 ∙ 35 = 70 (см²) — площадь боковой поверхности

б) S_полн. = S_{бок.пов.} + 2 ∙ S_осн = 70 + 2 ∙ 12 = 70 + 24 = 94 (см²) — площадь полной поверхности.

Источник

Измерения прямоугольного параллелепипеда и его свойства

Содержание:

Что такое прямоугольный параллелепипед — определение
Свойства параллелепипеда, какими обладают противолежащие грани
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Как найти диагональ и ширину прямоугольного параллелепипеда

Что такое прямоугольный параллелепипед — определение

Определение

Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.

Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.

В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

прямоугольный;
прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
ромбоэдр — шестигранная призма, грани которой — это ромбы;
куб — состоит из квадратных граней.

Определение

Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.

Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.

Параллелепипед

Источник: wikipedia.org

Прямоугольный параллелепипед, как и любой другой, состоит из:

основания;
граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
диагоналей — отрезков, соединяющих противоположные вершины;
диагоналей граней;
высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.

Определение

Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.

Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

Противолежащие грани равны друг другу и попарно параллельны.
Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
Фигура симметрична относительно середины диагонали.
Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

Все стороны — прямоугольники.
Все углы, состоящие из двух граней, равны 90°.
Любую сторону можно принять за основание.
Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Определение

Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.

(V=acdot bcdot h,)

где V — объем, a — длина, b — ширина, h — высота.

Примечание

Площадь боковой поверхности равна сумме площадей боковых граней.

(S_{бп}=2(ab+ac))

Примечание

Площадь полной поверхности равна сумме площадей боковых граней и оснований.

(S_{пп}=2(ab+bc+ac))

Как найти диагональ и ширину прямоугольного параллелепипеда

В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:

(d^2=a^2+b^2+c^2)

Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:

(sqrt{a^2+b^2+c^2})

Длина, ширина и высота, как правило, вычисляются через формулу объема:

(a=frac V{bh},;b=frac V{ah},;h=frac V{ab})

Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.

Источник