а) Найди сумму площадей всех граней прямоугольного параллелепипеда, если его измерения равны 5 см, 2 см и 3 см.
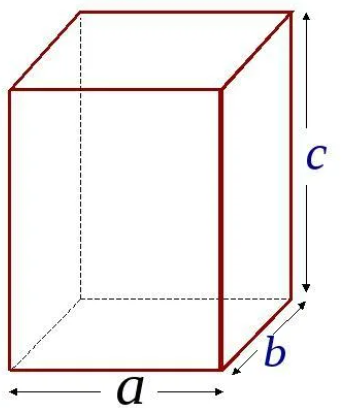
б) Напиши формулу площади поверхности прямоугольного параллелепипеда с измерениями a, b и c.
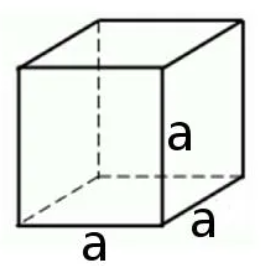
в) Напиши формулу площади поверхности куба со стороной a.
reshalka.com
ГДЗ учебник по математике 3 класс Петерсон. 31 урок. Формула объема прямоугольного параллелепипеда. Номер №7
Решение а
(5 * 3 + 5 * 2 + 3 * 2) * 2 = (15 + 10 + 6) * 2 = 31 * 2 = 62
(
с
м
2
)
− площадь всех граней.
Ответ: 62
с
м
2
Решение б
S = (a * b + a * c + c * b) * 2
Решение в
S = (a * a) * 6

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Прямоугольным параллелепипедом называется трехмерное тело, у которого противоположные грани параллельны и являются прямоугольниками. Проще говоря, прямоугольный параллелепипед представляет собой вытянутый куб.
Онлайн-калькулятор площади поверхности параллелепипеда
Прямоугольный параллелепипед можно охарактеризовать тремя числами — длинами его сторон: aa, bb, cc.
Формула площади поверхности параллелепипеда
Чтобы найти полную площадь поверхности параллелепипеда, нужно сложить площади всех его граней. Граней у параллелепипеда шесть, поэтому:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Но так как противоположные грани прямоугольного параллелепипеда равны между собой, то: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.
Поскольку гранями данного параллелепипеда являются прямоугольники, то их площади равны соответственно:
S1=S2=abS_1=S_2=ab
S3=S4=bcS_3=S_4=bc
S5=S6=acS_5=S_6=ac
Итак, полная площадь поверхности параллелепипеда:
S=2(ab+bc+ac)S=2(ab+bc+ac)
Из этой формулы следует, что если a=b=ca=b=c, то получим: S=6a2S=6a^2. Это и есть формула для площади поверхности куба со стороной aa.
Найдите площадь поверхности прямоугольного параллелепипеда со сторонами 2 см.2text{ см.}, 4 см.4text{ см.}, 6 см.6text{ см.}
Решение
a=2a=2
b=4b=4
c=6c=6
S=2(ab+bc+ac)=2(2⋅4+4⋅6+2⋅6)=88 (см. кв.)S=2(ab+bc+ac)=2(2cdot4+4cdot6+2cdot6)=88text{ (см. кв.)}
Ответ: 88 см. кв.88text{ см. кв.}
Найдите площадь поверхности прямоугольного параллелепипеда высотой 3 см.3text{ см.}, в основании которого лежит квадрат со стороной 1 см.1text{ см.}
Решение
a=b=1a=b=1
c=3c=3
S=2(ab+bc+ac)=2(1+3+3)=14 (см. кв.)S=2(ab+bc+ac)=2(1+3+3)=14text{ (см. кв.)}
Ответ: 14 см. кв.14text{ см. кв.}
Не знаете, где заказать задачу по геометрии? Обратитесь к нашим экспертам в данной области!
Тест по теме «Площадь поверхности параллелепипеда»
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).
Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
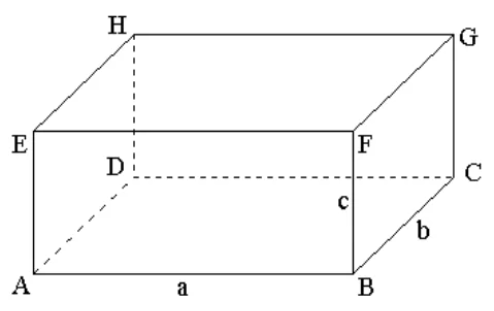
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
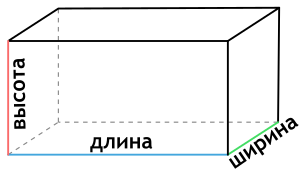
Длина, ширина, высота
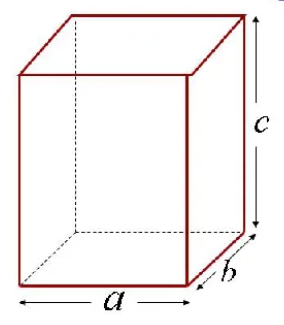
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
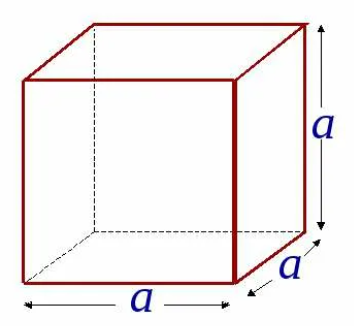
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда
Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
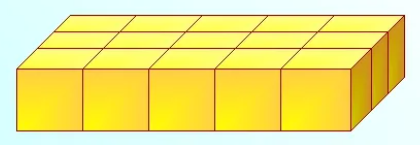
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
Рисунок 8
Пирамида
Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
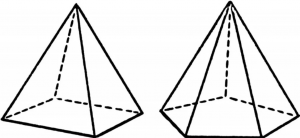
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
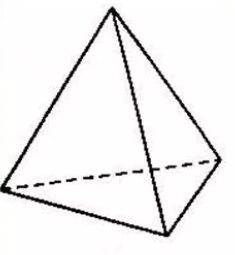
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 1.1k
Найдите правильный ответ на вопрос ✅ «1. найди сумму площадей всех граней прямоугольного параллелепипеда, если его измерения равны 5 см, 2 см, 3 см. 2. напиши формулу площади …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Математика » 1. найди сумму площадей всех граней прямоугольного параллелепипеда, если его измерения равны 5 см, 2 см, 3 см. 2. напиши формулу площади поверхности прямоугольного параллелепипеда с измерениями a, b, а. 3.