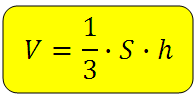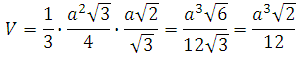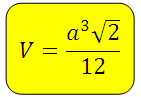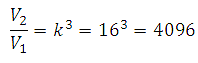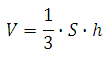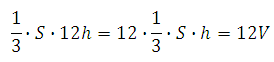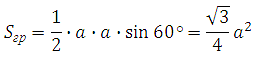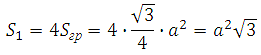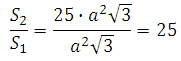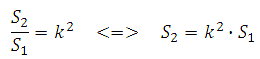Как найти сумму площадей всех граней тетраэдра - Исправление недочетов и поиск решений вместе с Examum.ru

Размещено 3 года назад по предмету
Математика
от NikolaiIvashenko

Ответ на вопрос

Ответ на вопрос дан
ewgenijbark

Если каждое ребро тетраэдра равно а, то каждый из треугольников, составляющих тетраэдр — правильный, со стороной а.
Площадь правильного треугольника
$S = frac{ sqrt{3} }{4}a^2$
Всего у тетраэдра 4 грани — треугольника⇒сумма площадей равна
$S = 4 * frac{ sqrt{3} }{4}a^2= sqrt{3}a^2$
1. Ответ на вопрос
  
  Ответ на вопрос дан
  NikolaiIvashenko
  
  блин, незнаю вчем дело, но учительница говорит, что неверно, тройку получил(
2. Ответ на вопрос
  
  Ответ на вопрос дан
  ewgenijbark
  
  в чем ошибка — не объяснила?
3. Ответ на вопрос
  
  Ответ на вопрос дан
  NikolaiIvashenko
  
  Там короче подругому все, немогу сказать, т.к. это был экзамен и лист она забрала. Но все равно спасибо.

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение тетраэдра
Виды тетраэдра
Формулы площади и объема правильного тетраэдра

Определение тетраэдра

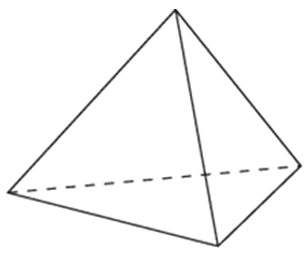
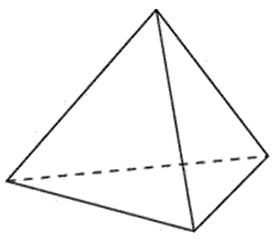
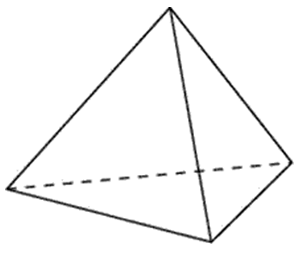
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.

Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.

Виды тетраэдра

Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.
Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.
Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.
Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.

Формулы площади и объема правильного тетраэдра

Площадь поверхности

Объем

Источник

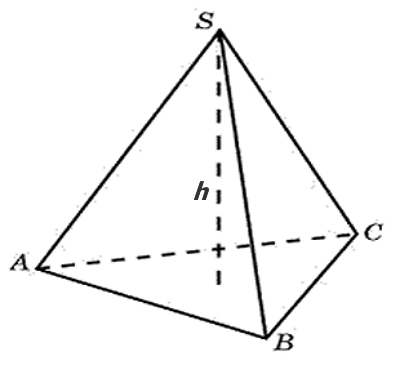
Объём тетраэдра. В данной статье мы с вами рассмотрим несколько заданий с пирамидами. Как известно, тетраэдр также является пирамидой. Определение тетраэдра:

Тетраэдр — это простейший многогранник, имеет 4 грани, которые являются треугольниками. Вершин у тетраэдра 4, к каждой вершине сходится 3 ребра, а всего ребер 6. Тетраэдр у которого грани равносторонние треугольники называется правильным.

Объём пирамиды (значит и тетраэдра):

S – площадь основания пирамиды h – высота пирамиды

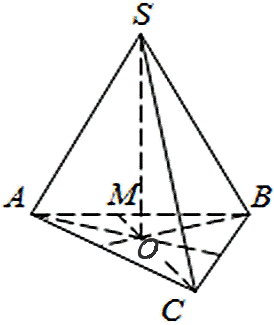
Вычислим объём правильного тетраэдра при ребре равном величине a.

Тогда площадь каждой грани будет равна (в данном случае и основания АВС):

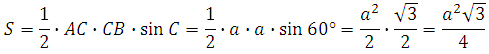
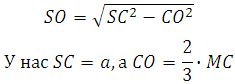
Вычислим высоту SO. Рассмотрим прямоугольный треугольник SOC:

*Известно, что биссектрисы треугольника точкой пересечения делятся в отношении 1 к 2.

Вычислим СM. По теореме Пифагора:

Следовательно:

Таким образом, объём тетраэдра будет равен:

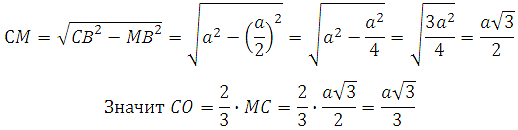
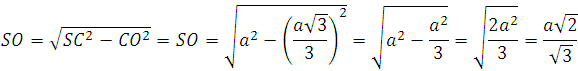
Смыл рассматриваемых ниже заданий таков – все ребра пирамиды, либо только высота увеличивается в несколько раз. Понятно, что при этом увеличивается объём пирамиды и площадь её поверхности. Далее требуется вычислить во сколько раз происходит это увеличение.

1. Если увеличивается только высота пирамиды и стоит вопрос об изменении объёма, то понятно, что он увеличивается прямопропорционально исходному объёму пирамиды, так как зависимость линейная. Проще говоря, объём увеличивается во столько же раз, во сколько увеличена высота.

2. Если речь идёт об увеличении всех рёбер пирамиды в определённое количество раз, то здесь необходимо понимать, что в итоге получается пирамида подобная исходной, причём её грани также подобны соответствующим граням полученной пирамиды.

Позволю себе, на данный момент, по вопросу подобия фигур и тел предложить Вам обратиться к теории изложенной в учебнике. В скором будущем обязательно размещу отдельную статью на эту тему.

Что касается представленной группы задач, то отмечу, что с использованием свойств подобия такие задания решаются практически в одно действие.

Вот что необходимо помнить и знать:

То есть, если мы увеличим все рёбра пирамиды в k раз, то отношение площади любой её грани к площади исходной соответствующей ей грани будет равно k². Естественно, что отношение полных площадей поверхностей таких пирамид также будет равно k².

А также:

То есть, если мы увеличим все рёбра пирамиды в k раз, то отношение объёма полученной пирамиды к объёму исходной будет равно k³. Рассмотрим задачи:

Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в шестнадцать раз?

Тетраэдр это пирамида, все грани которой равносторонние треугольники.

Данная пирамида и пирамида полученная увеличением всех её рёбер в 16 раз будут являться подобными, коэффициент подобия соответственно будет равен 16.

Объёмы подобных тел относятся как куб коэффициента подобия. То есть, как уже сказано, объём полученной пирамиды равен произведению куба коэффициента подобия и объёма исходной пирамиды:

Определим во сколько раз увеличится объём, найдём отношение объёмов:

Таким образом, если все ребра увеличить в 16 раз, то объём увеличится в 4096 раз.

*Можно решить задачу по другому. Обозначить ребро тетраэдра как а, далее выразить его высоту. После этого определить объёмы пирамид используя формулу, а далее найти отношение полученных объёмов. Но такой путь будет неоправданно долгим и потребует в разы больше времени на решение.

Ответ: 4096

Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в двенадцать раз?

Объем пирамиды равен одной трети произведения площади основания и высоты:

S – площадь основания

h – высота пирамиды

При увеличении высоты в 12 раз, объем пирамиды также увеличится в 12 раз (это прямолинейная зависимость):

Ответ: 12

Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в пять раза?

Отметим, что площадь поверхности тетраэдра равна сумме площадей его четырёх граней, которые являются правильными треугольниками.

Первый способ:

Определим площадь поверхности исходного тетраэдра и увеличенного, а затем найдём отношение площадей.

Пусть ребро тетраэдра равно а, тогда площадь грани будет равна:

*Использовали формулу площади треугольника.

Значит площадь поверхности исходного тетраэдра будет равна:

Если рёбра тетраэдра увеличить в 5 раз, то площадь поверхности изменится следующим образом:

Отношение площадей равно:

Таким образом, при увеличении ребер тетраэдра в пять раз, площадь его поверхности увеличится в 25 раз.

Второй способ:

Известно, что при увеличении (уменьшении) линейных размеров фигуры в k раз получается подобная ей фигура, их площади относятся как квадрат коэффициента подобия, то есть:

k – это есть коэффициент подобия

В данной задаче k=5.

То есть, с использованием свойства подобия задача решается устно:

*Площадь каждой грани пирамиды увеличится в 25 раз, а это означает, что площадь поверхности всей пирамиды также увеличится в 25 раз.

Ответ: 25

27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?

Данная задача от предыдущей ничем не отличается. Не имеет никакого значения идёт ли речь о тетраэдре, пирамиде, кубе, параллелепипеде или о другом многограннике. Если сказано, что все рёбра увеличиваются в одинаковое число раз, то полученные грани «нового» тела будут подобны соответствующим граням исходного тела. А это значит, что увеличение площади поверхности произойдёт в k²раз (где k это коэффициент подобия).

Ответ: 4

Можете посмотреть задачи с кубами. В них речь идёт об увеличении площади поверхности или объёма.

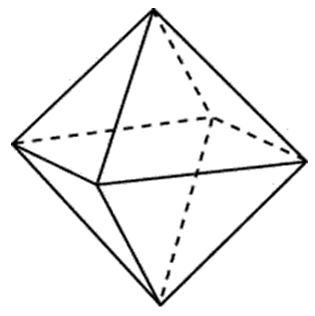
Ещё одна задача такого же класса. Но в условии речь идёт об октаэдре. Октаэдр это многогранник с восьмью граниями, все гарани это правильные треугольники.

27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

При увеличении рёбер в три раза каждая грань полученного октаэдра будет подобна соответствующей ей грани исходного. Площадь каждай грани увеличится в 3² раз, то есть в 9 раз. Значит и площадь всей поверхности также увеличится в 9 раз.

*Задача полностью аналогична двум предыдущим задачам, только здесь речь идет об октаэдре.

27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

Посмотреть решение

27089. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?

Посмотреть решение

27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?

Посмотреть решение

На этом всё. Успеха Вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Тетраэдр Яковлева Татьяна Петровна, доцент кафедры математики и физики

Тетраэдр

Яковлева Татьяна Петровна,
доцент кафедры математики и физики
Камчатского государственного университета имени Витуса Беринга,
кандидат педагогических наук, доцент,
г. Петропавловск — Камчатский

Тетра́эдр. Тетраэдр(или треугольная пирамида) имеет сходство с треугольником, но в отличие от него является более сложной фигурой и не удивительно, что его свойства более разнообразны

1. Тетра́эдр.

Тетраэдр(или треугольная пирамида) имеет сходство с треугольником, но в отличие от него является более сложной фигурой и не удивительно, что его свойства более разнообразны.
Тетраэдр – это простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер

Свойства тетраэдра. Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед

2. Свойства тетраэдра.

Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части.

Типы тетраэдров. Равногранный тетраэдр, у которого все грани — равные между собой треугольники

3. Типы тетраэдров.

Равногранный тетраэдр, у которого все грани — равные между собой треугольники.

Ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке

Ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.

Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой

Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.

Каркасный тетраэдр — тетраэдр, отвечающий любому из следующих условий: существует сфера, касающаяся всех ребер, суммы длин скрещивающихся ребер равны, суммы двугранных углов при противоположных ребрах…

Каркасный тетраэдр — тетраэдр, отвечающий любому из следующих условий:
существует сфера, касающаяся всех ребер,
суммы длин скрещивающихся ребер равны,
суммы двугранных углов при противоположных ребрах равны,
окружности, вписанные в грани, попарно касаются,
все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.

Соразмерный тетраэдр, бивысоты которого равны

Соразмерный тетраэдр, бивысоты которого равны.
Инцентрический тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.

Тетраэдры в микромире. Правильный тетраэдр образуется при sp3-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной…

4. Тетраэдры в микромире.

Правильный тетраэдр образуется при sp3-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника.
Молекула метана СН4
Ион аммония NH4+
Сульфат-ион SO42-, Фосфат-ион PO43-, Перхлорат-ион ClO4- и многие другие ионы
Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4]-, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-

Тетраэдры в живой природе.

5. Тетраэдры в живой природе.

Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.

Тетраэдры в технике Тетраэдр образует жёсткую, статически определимую конструкцию

6. Тетраэдры в технике

Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр.

Формулы. Площадь полной поверхности тетраэдра можно рассчитать, зная площади его граней

7. Формулы.

Площадь полной поверхности тетраэдра можно рассчитать, зная площади его граней.

Из основной формулы для объёма тетраэдра

(1)

где S – площадь любой грани, а H – опущенная на нее высота, можно вывести еще целый ряд формул, выражающих объём через различные элементы тетраэдра. Приведем эти формулы для тетраэдра ABCD.

(2)

где ∠(AD,ABC) – угол между ребром AD и плоскостью грани ABC;

ABC,ABD) – угол между гранями ABC и

(3)

где ∠(ABC,ABD) – угол между гранями ABC и ABD;

(4)
где |AB,CD| – расстояние между противоположными ребрами AB и CD, ∠(AB,CD) – угол между этими ребрами.
Формулы (2)–(4) можно использовать для нахождения величин углов между прямыми и плоскостями; особенно полезна формула (4), с помощью которой можно находить расстояние между скрещивающимися прямыми AB иCD.
Формулы (2) и (3) аналогичны формуле S = (1/2) absin C для площади треугольника. Формуле S = rp аналогична формула,

(5)
где r – радиус вписанной сферы тетраэдра, Σ – его полная поверхность (сумма площадей всех граней). Имеется и красивая формула, связывающая объём тетраэдра с радиусом R его описанной сферы (формула Крелле):

AB×CD, AC×BD,AD×BC). Из формулы (2) и теоремы косинусов для трехгранных углов (см

(6)

где Δ – площадь треугольника, стороны которого численно равны произведениям противоположных ребер (AB×CD, AC×BD,AD×BC). Из формулы (2) и теоремы косинусов для трехгранных углов (см. Сферическая тригонометрия) можно вывести формулу, аналогичную формуле Герона для треугольников:

(7)
где α, β, γ – плоские углы BDC, CDA, ADB при вершине D, δ = (α+β+γ)/2 – их полусумма.
Наконец, приведем векторную формулу:

(8)

где внутри модуля стоит смешанное произведение векторов. С помощью этой формулы можно вычислять объём тетраэдра, зная координаты его вершин.

Задачи. Задача №1. Точки М и

8. Задачи.

Задача №1.
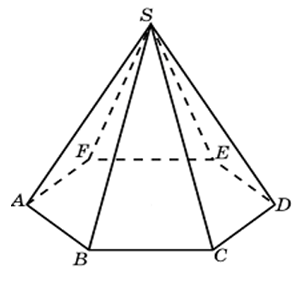
Точки М и N – середины ребер АВ и АС тетраэдра АВСD (рис. 1). Докажите, что прямая МN параллельна плоскости ВСD. Найдите длину отрезка МN, если ВС = а.

Решение: АМ = ВМ, так как

Решение:
АМ = ВМ, так как М – середина отрезка АВ, АN = СN, так как N — средина отрезка АС. МN – средняя линия треугольника АВС. По свойству средней линии, МN параллельна ВС и .
Прямая МN параллельна прямой ВС, которая лежит в плоскости ВСD, и не лежит в плоскости ВСD. Значит, по признаку параллельности прямой и плоскости, прямая МN параллельна плоскости ВСD, что и требовалось доказать.

Задача № 2. Через середины ребер

Задача № 2.
Через середины ребер АВ и АС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SАB и SBС по параллельным прямым.

Доказательство: Обозначим середины ребер

Доказательство:
Обозначим середины ребер АВ и АС – как М и N соответственно, а плоскость, проходящую через точки М и N параллельно ребру SB, как φ.
Плоскость АВS проходит через прямую SB, параллельную плоскости φ и пересекает эту плоскость по прямой МL, . Значит, прямая МL параллельна прямой SB.
Плоскость ВSС проходит через прямую SB, параллельную плоскости φ и пересекает эту плоскость по прямой NP, . Значит, прямая PN параллельна прямой SB.
Имеем, что две прямые МL и NP параллельны одной и той же прямой SB. Значит, прямые МL и NP параллельны, что и требовалось доказать.

Задача № 3. Докажите, что плоскость, проходящая через середины ребер

Задача № 3.
Докажите, что плоскость, проходящая через середины ребер АВ, АС и AD тетраэдра ABCD параллельна плоскости BCD.

Доказательство: Пусть А1,

Доказательство:
Пусть А1, В1, С1 – середины ребер АВ, АС и AD тетраэдра ABCD (рис. 3). Докажем, что плоскость А1В1С1параллельна плоскости BCD.
А1С1 – средняя линия треугольника АВD. Из свойств средней линии следует, что А1С1параллельна BD.А1В1 – средняя линия треугольника АСD. Из свойств средней линии следует, что А1В1параллельна СD. Прямые А1С1и А1В1 пересекаются в точке А1. По признаку параллельности плоскостей, плоскости А1В1С1 и BCD параллельны, что и требовалось доказать.

Задача № 4. а) Постройте сечение тетраэдра

Задача № 4.
а) Постройте сечение тетраэдра АBCD плоскостью α, проходящей через точку М ребра ВD, параллельно ребрам АD и ВС.
б) Докажите, что полученное сечение – параллелограмм.
в) Найдите углы полученного в сечении параллелограмма, если угол между прямыми АD и ВС равен 𝜑.

Построение: 1) Проведем прямую

а) Построение:
1) Проведем прямую ML параллельно прямой АD в плоскости АDВ .
2) Проведем прямую MN параллельно прямой BC в плоскости BCD .
3) Проведем прямую NP параллельно прямой АD в плоскости АDC .
4) Проведем прямую LP.
5) Так как прямая АD не лежащая в плоскости MNL параллельна прямой ML, лежащей в плоскости MNL, то прямая АD параллельна MNL по признаку. Так как прямая ВС, не лежащая в плоскости MNL параллельна прямой MN, лежащей в плоскости MNL, то прямая ВС параллельна MNL по признаку. Значит, MNLP – искомое сечение.
б) Докажем, что сечение MNLP – параллелограмм. Прямые МL и NP параллельны одной и той же прямой АD. Значит, прямые МL и NP параллельны. Прямые МN и LP параллельны одной и той же прямой ВС. Значит, прямые МN и LP параллельны. Имеем, что в четырехугольнике МNLP противоположные стороны попрано параллельны, по определению, МNLP – параллелограмм.
в) Заметим, что прямые АD и ВС – скрещивающиеся прямые (по признаку скрещивающихся прямых). Угол между скрещивающимися прямыми АD и ВС равен либо углу МLP, либо углу LМN. Сумма углов параллелограмма, прилежащих к одной стороне равна π. Значит, в этом параллелограмме углы равны либо 𝜑, либо π – 𝜑.

БИБЛИОГРАФИЯ Геометрия: учеб. для 10-11кл

БИБЛИОГРАФИЯ

Геометрия: учеб. для 10-11кл. сред. шк./ Атанасян Л.С., Бутузов В.Ф. и др.,- М.: «Просвещение», 2010.-255с.
Поурочные разработки по геометрии. Дифференцированный подход: для 10-11кл./ Яровенко В.А.-М.: «Вако», 2011-336с.
ru.wikipedia.org/wiki/Тетраэдр
dic.academic.ru/dic.nsf/enc1p/47402

Источник

Объем тетраэдра

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

S – площадь любой грани,
H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

Все грани равны.
Все плоские углы правильного тетраэдра равны 60°
Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим

Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Нахождение объема тетраэдра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем тетраэдра и разберем примеры решения задач для закрепления материала.

Формула вычисления объема тетраэдра

1. Общая формула (через площадь основания и высоту)

Объем (V) тетраэдра считается также, как и объем любой пирамиды. Он равняется одной третьей произведения площади любой грани и высоты, опущенной на нее:

2. Объем правильного тетраэдра

В правильном тетраэдре все грани являются равносторонними треугольниками. Объем данной фигуры равен одной двенадцатой произведения длины его ребра в кубе на квадратный корень из числа 2.

Т.к. это правильный тетраэдр, все его ребра равны (AB = BC = AC = AD = BD = CD).

Примеры задач

Задание 1
Площадь одной из граней тетраэдра равна 24 см 2 , а высоту, опущенная на нее – 9 см. Найдите объем фигуры.

Решение:
Применим общую формулу и получаем:

Задание 2
Дан правильный тетраэдр, ребро которого равняется 8 см. Найдите его объем.

Решение:
Воспользуемся формулой для расчета объема правильной фигуры:

Объем тетраэдра площадь треугольника

Из основной формулы для объёма тетраэдра

(1),

(2) ,

где ∠ (AD,ABC) – угол между ребром AD и плоскостью грани ABC;

(3) ,

где ∠ (ABC,ABD) – угол между гранями ABC и ABD;

(4) ,

где |AB,CD| – расстояние между противоположными ребрами AB и CD, ∠ (AB,CD) – угол между этими ребрами.

Формулы (2)–(4) можно использовать для нахождения величин углов между прямыми и плоскостями; особенно полезна формула (4), с помощью которой можно находить расстояние между скрещивающимися прямыми AB иCD.

Формулы (2) и (3) аналогичны формуле S = (1/2)absin C для площади треугольника. Формуле S = rp аналогична формула

(5) ,

где r – радиус вписанной сферы тетраэдра, Σ – его полная поверхность (сумма площадей всех граней). Имеется и красивая формула, связывающая объём тетраэдра с радиусом R его описанной сферы (формула Крелле):

(6) ,

где Δ – площадь треугольника, стороны которого численно равны произведениям противоположных ребер (AB × CD, AC × BD,AD × BC). Из формулы (2) и теоремы косинусов для трехгранных углов (см. Сферическая тригонометрия) можно вывести формулу, аналогичную формуле Герона для треугольников:

(7) ,

где α, β, γ – плоские углы BDC, CDA, ADB при вершине D, δ = (α+β+γ)/2 – их полусумма.

Наконец, приведем векторную формулу:

(8) ,

источники:

Нахождение объема тетраэдра: формула и задачи

http://school-collection.edu.ru/dlrstore-wrapper/41cad97f-3245-422f-b97f-30dddea784f0/Obem_tetraedra.html

Источник