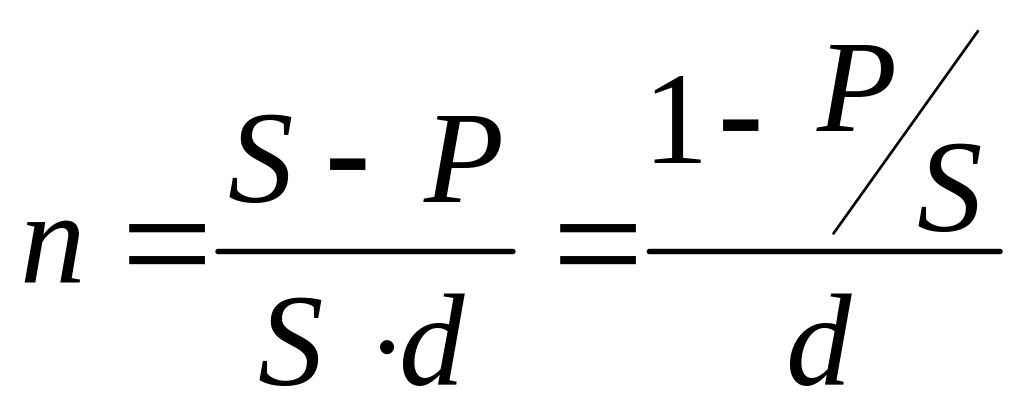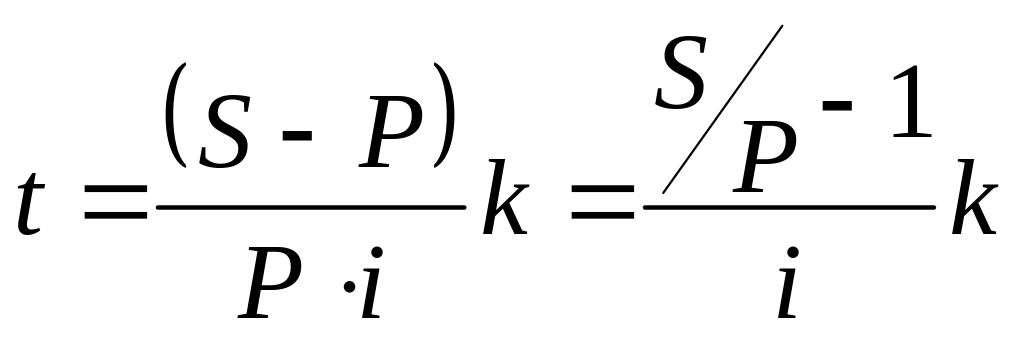Исчислите процентные деньги, уплаченные за пользование ссудой размером 1 млн. руб. в течение полугода. Ставка по кредиту – 60% годовых.
Решение:
Процентные деньги или проценты – это сумма, которую уплачивают за пользование денежными средствами. Это абсолютная величина дохода.
Сумма процентных денег рассчитывается по формуле:
PV – настоящая (исходная или современная) стоимость денег,
t – срок операции,
Y – продолжительность года, выражается в тех же единицах, что и t,
i – ставка процентов за период.
/formula-rascheta-procentov-po-vkladam.jpg)
Общая формула расчета процентов по вкладу
Формула для вкладов с ежемесячной капитализацией
Формула для вкладов с ежедневной капитализацией
Формула для вкладов с ежеквартальной капитализацией
Что такое эффективная ставка по депозиту?
Как рассчитать через Excel?
Налоги на доход по вкладам
Подробнее про формулу
Банки в своей практике руководствуются несколькими формулами, позволяющими рассчитывать простые % и сложные. При их начислении применяется фиксированный и плавающий вид ставок. Фиксированную закрепляют договором при размещении вклада, она не меняется до конца периода его действия. Она может измениться в случае автоматических пролонгаций действия договора. Также она изменится в случае досрочного разрыва соглашения между клиентом и банком с выплатой % за фактический период размещения вложений, если вклад был размещен до востребования. Эти нюансы должны быть описаны в договорах.
В случае плавающих ставок, установленных изначально, их размер может изменяться на протяжении действия договоров.
При каких условиях и в каком порядке будет осуществляться этот процесс, нужно описывать в договорах. Изменение процентов привязано к изменениям:
- ключевой ставки;
- валютного курса;
- переводом депозита в иную категорию и др.
Для расчетов указываются все требуемые формой данные:
- сумма вклада;
- размер % ставки конкретного вклада;
- периодичность начислений % (поквартально, помесячно, ежедневно и др.);
- срок заключения договора;
- иногда нужно знать вид применяемой ставки – она может плавать или быть зафиксированной.
Общая формула расчета процентов по вкладу
Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.
Выбирая вклад, клиент банка должен обратить внимание на порядок, который применяется при начислении процентов.
Формула расчета простых:
S = (P x I x t / K) / 100
Обозначения:
- S – прибыль со вклада (только проценты, без тела вклада);
- P – сумма, изначально внесенная на депозит;
- I – размер % ставки (за год);
- t – кол-во дней начисления %;
- K – кол-во дней за год по календарю.
A = P * (1 + r/n)^(n*t)
Здесь все более сложно, поскольку нужно высчитывать степень (^ – знак степени). Остальные обозначения:
- A – общая сумма денег (тело вклада + проценты), которую вы получите после того, как срок вклада закончится.
- P – стартовая сумма, которую вы кладете на счет вклада.
- r – процентная ставка по вкладу.
- n – количество расчетов прибыль в году, для ежедневной капитализации – 365 или 366, для ежемесячной – 12 и так далее.
- t – количество лет вклада. 6 месяцев – это 0.5 года.
Формула для вкладов с ежемесячной капитализацией
Чтобы рассчитать возможную прибыль в случае выбора вида депозита с капитализацией % с ежемесячным начислением % подойдет такая формула:
S = Р * (1 + (N/100)/12)^n, здесь используются следующие обозначения:
n – количество проведенных операций перевода процентов в тело вклада на протяжении полного срока действия договора (то есть месяцев вклада);
S – сумма вклада на дату окончания действия депозита, которую вкладчик получит на руки;
Р – изначально внесенная сумма на депозит с возможностью капитализации;
N — % ставка (годовая).
Формула для вкладов с ежедневной капитализацией
Если выбрана форма начисления % с ежедневной капитализацией, применяется следующая формула:
S = P * (1 + (N/100)/K)^T, где:
S – суммарный доход (тело вклада + проценты);
Р – внесенная при заключении договора сумма;
N – годовая % ставка;
К – 365 или 366 дней;
Т – кол-во дней, на которые открыт депозит.
Формула для вкладов с ежеквартальной капитализацией
В данном случае расчет процентов будет выглядеть следующим образом:
S=Р * (1+ (N/100)/4)^Т, где:
S — получаемый в конце срока доход (тело вклада + проценты);
Р – изначально размещенная сумма на депозите;
N — годовой %;
Т – количество кварталов, на протяжении которых открыт вклад.
Что такое эффективная ставка по депозиту?
Эффективная ставка = фактическая ставка + прибыль от капитализации. Если вклад – без капитализации, то эффективная ставка равна фактической ставке (указана в договоре); если вклад – с капитализацией, то эффективная ставка будет выше фактической, поскольку капитализация будет увеличивать тело вклада.
Как рассчитать через Excel?
Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 24 месяца, нужно составить таблицу:
- A1-A24 – указываем месяцы, то есть 1,2,3…
- D1 – указываем сумму тела кредита.
- D2 – указываем ставку в процентах
Теперь нужно в ячейку B1 вставить специальную формулу для подсчета сложного процента: =БС($D$2/12;A1;;-$D$1). Первый аргумент ($D$2/12) – проценты, нужно делать на 12, поскольку считаем ежемесячное начисление. Второй аргумент (A1) – месяц, за который считаем. Третий аргумент оставляем пустым (комиссии/сборы). Четвертый (-$D$1) – тело вклада, ввиду некоторых особенностей работы функции БС его нужно указывать с минусом. Теперь выделяем ячейку B1, растягиваем ее содержимое на ячейки ниже, до B24. Получаем суммарное количество денег на счете в каждом месяце, через 24 месяца получим 58 644 рубля.
Как рассчитать онлайн?
Онлайн расчет процентов можно осуществлять на сайте банка, выбранного для размещения депозита. Для этого нужно найти на странице банка онлайн калькулятор вкладов, ввести в него требуемые данные и рассчитать:
- сумму;
- срок;
- дату начала размещения вклада;
- % ставку;
- период капитализации;
- пополнение (если возможно).
Пример расчета
Расчет при ежемесячной капитализации:
Исходные данные:
Сумма вклада – 50 000 руб.;
Годовая ставка — 8%;
Срок вклада – 12 мес.
50 000 х(1+0,08/12)^12= 54 150 руб.
Налоги на доход по вкладам
За 2021 и 2022 годы налог по вкладам не начисляли вовсе. На доход со вкладов, полученный с 1 января 2023 года, начисляется НДФЛ в размере 13%, но – только на доход, превышающий определенный порог. Порог рассчитывается так: берут максимальную ключевую ставку ЦБ РФ за год, после чего умножают ее на 1 000 000 рублей. Например, максимальная ключевая ставка составила 6% – значит, налогом не будет облагаться доход за год в 60 000 рублей. Если ваш доход за год превысил эту сумму – на сумму превышения начисляется 13%. Если вы получили за год 90 000 рублей дохода со вкладов – с 30 000 рублей нужно будет заплатить 13% НДФЛ, то есть 3 900 рублей. Налог рассчитывается автоматически, в 2024 году вам пришлют уведомление за 2023-й год. Это работает как для резидентов, так и для нерезидентов РФ.
Загрузить PDF
Загрузить PDF
Если вам довелось решать проблему нахождения общей суммы денег, выплачиваемых за определенный период времени, не волнуйтесь. Такие задачи довольно легко решать, если знать, что обозначают отдельные составляющие формулы и как их использовать.
-
1
Поймите единицы, с которыми будете работать в формуле для расчета процентной ставки. Когда вы решаете задачу нахождения размера процентной ставки, к примеру, процент кредитования, который будет начисляться за взятый вами заем, вы будете работать с несколькими переменными величинами. Они включают в себя:
- P = основная сумма займа.
- i = процентная ставка.
- N = период займа, в годах.
- F = общая сумма, выплаченная в конце обозначенного периода лет.
-
2
Знайте, формулу, которую нужно использовать, чтобы вычислить общую сумму, которую вы выплатите. Чтобы найти итоговую сумму, выплачиваемую в конце установленного срока, за который вы должны выплатить ваш заем, вам нужно умножить основную сумму кредита на сумму процентной ставки и 1. Затем, возвести эту сумму в степень, равную количеству лет. Сама формула выглядит вот так:
- F = P(1 + i)^N
-
3
Пробегитесь по вышеприведенной формуле и определите, какие числа подставляются в какие переменные. В большинстве случаев, задачи на процентные ставки будут приведены в письменном виде, а вам нужно будет догадаться, какое число и что оно представляет. К примеру, вам дано: «вы заняли $4000 в банке и обязались вернуть изначальный заем с начисленным процентом через 4 года по ставке 10% в год. Какую сумму вы заплатите через 4 года?».
- P будет $4,000.
- i будет 10%.
- N будет 4 года.
- F будет искомым ответом.
-
4
Подставьте известные числа в формулу по фиксированной процентной ставке. Как только вы поняли, какие числа и что обозначают, подставьте их в формулу, чтобы найти фиксированную ставку. Наша формула будет выглядеть следующим образом:
- F = 4000(1 + 10%)^4. Нужно отметить, что легче всего решать задачу, если вы переведете ставку в процентах в десятичный вид, так, что формула примет вид F = 4000(1 + 0.1)^4
Реклама
-
1
Работайте над решением поэтапно. Для того чтобы найти общую сумму, которую вы выплатите за установленный займом срок, вам придется действовать поэтапно. Давайте разберем пример в этой статье:
- Вы взяли кредит в банке на сумму в $5000 и планируете выплатить всю изначальную сумму плюс накопленные проценты за 5 лет. Ставка кредитования равна 10%. Какую итоговую сумму вы заплатите через 5 лет?
-
2
Создайте свою формулу. Как только вы закончили читать задачу, напишите формулу на основе стандартного равенства F = P(1 + i)^N. Для нашей задачи формула примет такой вид:
- F = 5000(1 + 0.1)^5.
-
3
Для начала, вычислите то, что в скобках. Когда вы выписали свою формулу, начните ее решать. Первым этапом будет нахождение того, что в скобках. В нашем случае:
- Решите (1 + 0.1) = 1.1. Теперь наше равенство выглядит вот так: F = 5000(1.1)^5.
-
4
Далее, используйте N для решения следующей части равенства. Как только вы упростили выражение в скобках, вам нужно включить года (N) в формулу. То есть, нужно возвести выражение в скобках в степень N. В нашем случае:
- (1.1)^5 означает умножение 1.1 на само себя пять раз. То есть, (1.1)^5 = 1.61051.
-
5
Закончите решать равенство. Сейчас у вас должен остаться последний шаг для решения всего равенства. Чтобы завершить вычисление по формуле и найти F, или итоговую сумму выплат, вам нужно умножить P на значение в скобках. В нашем случае:
- F = 5000(1.61051) тем самым, F = $8,052.55. Это означает, что через 5 лет вам придется выплатить $8,052.55.
Реклама
Советы
- Не забудьте перевести процентную ставку (%) в десятичный вид.
Реклама
Об этой статье
Эту страницу просматривали 8472 раза.
Была ли эта статья полезной?
Рассчитываем проценты по вкладу: формула и примеры
Чтобы выяснить, какой доход принесет вклад, недостаточно знать годовую ставку. На прибыльность также методика начисления банком процентов. В финансовой системе существуют понятия простого и сложного процента, позволяющего получить при почти равных условиях разный доход по вкладам.
Рассчитать проценты по вкладу можно самостоятельно без помощи специалиста. В статье разбираем особенности каждой схемы и объясняем, как работать с формулами.
Простые проценты
Это вознаграждение, которое начисляется на начальную сумму вклада за определенный период. Простые проценты не прибавляются к телу депозита и выплачиваются либо по истечении срока договора, либо раз в месяц или год по выбору вкладчика. Если договор продлевается на новый срок, то прибыль за предыдущий период также не суммируется с вкладом.
Такая методика начисления применяется, как правило, для вкладов с возможностью пополнения и снятия средств. Процентная ставка в этом случае ниже, чем при начислении сложных процентов. Это объясняется тем, что ваш вклад — финансовый инструмент получения прибыли банком. И чем меньше уверенности, что вы не заберете деньги раньше срока, тем ниже вероятность долгосрочного инвестирования капиталов банком, а значит — и ниже доход.
Сложные проценты или капитализация
В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.
Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени. Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.
Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.
Расчет простых процентов
Выяснив годовую ставку, периоды и виды начисления процентов, можно посчитать доход по вкладу.
Простые проценты начисляются по следующей формуле:
где:
S — выплаченные проценты,
P — первоначальная сумма вложений,
I — годовая ставка,
T — количество дней вклада,
K — количество дней в году — 365 или 366.
Если вкладчик открыл депозит на 350 000 руб. сроком на 9 месяцев под 4,7%, процентный доход по вкладу составит:
Расчет сложных процентов
Чаще всего банки предлагают программы с ежемесячной капитализацией. Выбирая условия по вкладу, помните об общей закономерности: чем реже проценты прибавляются к телу депозита, тем меньше доход.
Ежедневная капитализация
Рассчитать доход за каждый день действия вклада поможет следующая формула:
где
Дв — сумма на конец срока, включая сумму открытия и начисленный процент,
Р — первоначальный размер депозита,
N — годовая процентная ставка, разделенная на 100,
К — количество дней в году — 365 или 366,
Т — срок вложения в днях.
Если клиент внес 350 000 руб. под 4,7% на 9 месяцев или 273 дня, в конце срока он получит:
Возвести число в большую степень можно на инженерном калькуляторе, где есть функция x^y, воспользоваться онлайн-сервисами или калькуляторами на сайтах банков.
Зная Дв, легко вычислить сумму процентов по вкладу за весь период:
Ежемесячная капитализация
Когда банк суммирует доход по депозиту раз в месяц, расчет ведется по формуле:
где:
Дв — итоговый доход, то есть размер вклада на конец срока включая сумму открытия и начисленный процент,
P — начальный депозит,
N — годовая ставка, разделенная на 100,
T — срок договора в месяцах.
Рассчитаем итоговую сумму с теми же исходными данными:
Процентный доход составит 12 532,56 ₽
Ежеквартальная капитализация
При начислении вознаграждения каждый квартал, а не раз в месяц, понадобится формула:
в ней Т — количество кварталов в сроке, остальные обозначения прежние.
Рассчитаем тот же вклад в конце срока:
Доход в виде процентов составит 12 483 ₽.
Но следует помнить: чем дольше срок размещения депозита, тем выше ставка. Поэтому при внесении денег на депозит надо сравнить условия с фактической ставкой, применяемой по выбранными вами условиям.
Итоги
Из таблицы видна разница доходов по методу простых и сложных процентов при равных условиях.
| Проценты по вкладу | Доход, руб. |
|---|---|
|
Простые |
12 303 |
|
Сложные: |
|
|
ежедневные |
12 521 |
|
ежемесячные |
12 532 |
|
ежеквартальные |
12 483 |
Однако нельзя однозначно утверждать о предпочтительности сложных процентов для каждого клиента. Оптимальная схема, тип банковского депозита — накопительный счет или вклад — зависят от ваших планов и потребностей:
- желаемый срок действия вклада и вероятность досрочного снятия средств
- необходимость регулярно пополнять счет или снимать средства
- необходимость регулярно снимать проценты
Если закрыт вклад до срока, вне зависимости от того, срочный он или до востребования, банк может применить санкции:
- Пересчитать процент по простой ставке до востребования. Законодательно ее размер не установлен, но большинство банков выплачивают всего 0,1–0,01%.
- Оставить половину или даже треть начальной ставки и тоже сделать перерасчет процентов.
Поэтому перед открытием депозита четко определите его срок и назначение. Райффайзен Банк предлагает банковские вклады без ограничений по снятию и пополнению, где проценты можно получать ежемесячно или добавлять к сумме депозита.
Эта страница полезна?
99
% клиентов считают страницу полезной
Следите за нами в соцсетях и в блоге
Предмет Финансовый менеджмент
1. Понятие процентные деньги.
2. Процентные ставки и их виды. Наращение.
Дисконтирование.
3. Эквивалентность процентных ставок.
4. Методики учета инфляции в финансовых
вычислениях
1. Понятие «процентные деньги»
Под процентными деньгами или
процентами понимают абсолютную величину
дохода от предоставления денег в долг
в любой из форм:
-
Выдача денежной ссуды
-
Продажа в кредит
-
Помещение денег на сберегательный счет
-
Учет векселя
-
Покупка сберегательного сертификата,
облигаций и т.д.
Какой бы вид не имели проценты, это
всегда конкретное проявление экономической
категории ссудный процент
Для определения его величины используют
договорную процентную ставку, т.е.
отношение суммы процентных денег,
выплачиваемых за фиксированный отрезок
времени, к величине ссуды.
Если ставка измеряется в виде десятичной
дроби, то в контракте ее фиксируют с
точностью до 1/16 и точнее. В формулах
вычисления делают подстановку в долях.
В финансовом количественном анализе
процентные ставки применяются не только
как инструмент приращения суммы долга,
но и в более широком смысле – как
измерители степени доходности
(эффективности) финансовых операций
вне зависимости от того, имел или нет
место процесс передачи денежных средств
и нарастания суммы долга.
2. Процентные ставки и их виды.
В зависимости от формы осуществления
финансовой операции или от условий
контракта, используют различные концепции
начисления процента – на базе простой
и сложной ставок процента, КОТОРЫЕ
ОТЛИЧАЮТСЯ ДРУГ ОТ ДРУГА БАЗОЙ ДЛЯ
НАЧИСЛЕНИЯ ПРОЦЕНТА.
1) Простая ставка процента
Если ставка процента применяется к
постоянной исходной базе на протяжении
всего периода договора, то говорят об
использовании простой процентной
ставки.
Под наращенной суммой ссуды (долга,
депозита и т.д.) понимается ее первоначальная
сумма вместе с начисленными на нее
процентами к концу срока.
Наращенная сумма определятся умножением
первоначальной суммы на множитель
наращения, который показывает во
сколько раз наращенная сумма больше
первоначальной суммы.
Для записи формул используют следующие
общепринятые обозначения:
I – проценты за весь срок
P – первоначальная сумма
S – наращенная сумма, т.е.
P + I
i – ставка процента
Начисление процентов за один период:
За n периодов:
Процесс изменения суммы долга с начисление
простых процентов описывается
арифметической прогрессией, члены
которой:
Формула для расчета наращенной суммы
по простой процентной ставке имеет вид:
— множитель наращения
*Примечание: выделяют три
варианта расчета процентов:
-
точные проценты с точным числом дней
ссуды (год – 365 дней, полугодие – 182 дня) -
обыкновенные проценты с точным числом
дней ссуды (банковский способ). Дает
несколько больший результат, чем
применение точных процентов (год – 360
дней) -
обыкновенные проценты с приближенным
числом дней ссуды. Используют, как
правило, для промежуточных вычислений,
не требующих абсолютной точности (месяц
– 30 дней всегда).
Дифференцирование по простой ставке
процента
Финансовый менеджер может столкнуться
с задачей, обратной определению наращенной
суммы – по заданной сумме S,
которую следует уплатить через время
n нужно определить сумму
полученной ссуды, т.е. P.
Ситуация для такого рода расчетов –
разработка условий контракта, удержание
процентов сразу при выдаче ссуды и др.
В таких случаях говорят, что сумма S,
дисконтируется, а сам процесс начисления
и удержания процентов вперед наз. учетом.
Проценты в виде разницы S
– P = D, наз.
дисконтом
Термин «дисконтирование» употребляется
и в более широком смысле – как средство
определения любой стоимостной величины
на некоторый момент времени при условии,
что в будущем она составим величину S,
вне зависимости от того, имела ли место
финансовая операция, предусматривающая
начисление процента или нет.
Величину P, найденную
дисконтированием S, наз.
приведенной (P’)
С помощью дисконтирования учитывается
фактор времени. Формулу расчета величины
P получаем из базовой ф.
расчета наращенной суммы:
,
отсюда:
(формула математического дисконтирования)
— множитель дисконтирования. Показывает,
какую долю составляет P
в S.
*Примечание: если n
≠ целому числу лет, тогда:
где t – число дней сделки
k – временная база,
т.е. число дней в году
Определение продолжительности ссуды:
в годах:
в днях:
где d – учетная ставка
Определение уровня процентной ставки
Это бывает необходимо при сравнении
контрактов по степени доходности в
случае, когда проценты в явном виде не
указаны. Решив уравнения наращения
относительно i и d,
получим:
Процентная ставка:
Учетная ставка:
где k – временная база
Формула для расчета наращенной суммы
для учетной ставки:
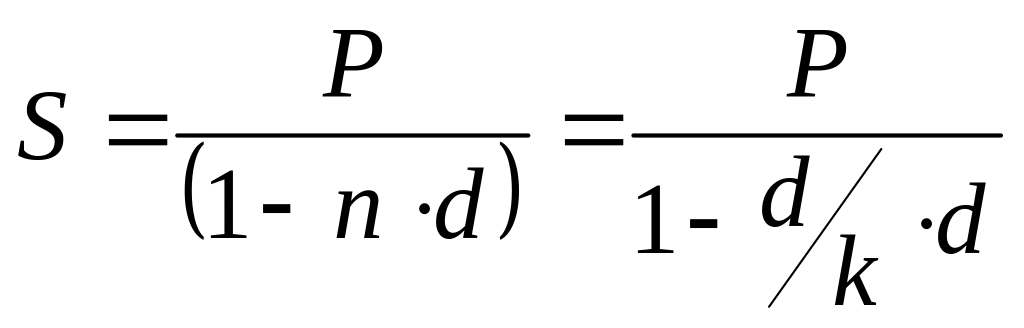
В мировой практике выделяют и такие 2
концепции начисления процентов:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

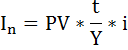
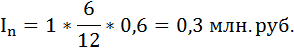
/formula-rascheta-procentov-po-vkladam-2.jpg)

/formula-rascheta-procentov-po-vkladam-4.jpg)