|
nonameprogger 1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
||||
|
1 |
||||
Найти сумму произведений по строкам матрицы14.01.2021, 18:01. Показов 2588. Ответов 26 Метки нет (Все метки)
как теперь сложить эти два числа(s)?
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 18:07 |
2 |
|
nonameprogger, что-то я не совсем понял суть задачи. Напишите тот вариант задачи, который вам дали полностью. Потом будем решать
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 18:09 [ТС] |
3 |
|
Laborant666, есть массив(2×2) Изображения
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 18:13 |
4 |
|
nonameprogger, понял вас. Сейчас оттестирую ваш код. У вас как я вижу на первый взгляд записывается сумма первой и второй строки в одну и ту же переменную. Соответственно нет двух сумм в наличии, а только одна. Как решается? После прохождения первой строки скопировать значение s в другую переменную. Посчитать сумму второй строки и сложить s с числом в ранее скопированной переменной Добавлено через 58 секунд
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 18:14 [ТС] |
5 |
|
Laborant666, не сказанно,лучше через цикл
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 19:20 |
6 |
|
nonameprogger, хорошо. Пока попробуйте после рассчета суммы первой строки — сохранить результат в отдельную переменную, а потом после рассчета второй строки сложить s и число из новой переменной. А я подумаю над своим решением — опередите меня — я проиграл Добавлено через 59 минут
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 19:22 [ТС] |
7 |
|
Laborant666, я пытался сделать временную переменную и туда кинуть сумму 1 строки.но по итогу он суммировал 2 строку со второй.вот сижу ломаю голову,спасибо что вы все еще со мной
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 19:28 |
8 |
|
nonameprogger, Вам сдавать это срочно? Или у нас есть время? Я вам помогу, но даю шанс сообразить самому. Подсказка: у вас в вашем коде каждый раз s обнуляется при переходе к следующей строке. Где-то надо сохранить данные до перехода к новой строке. Только инициализируйте этот sum = 0; А прибавляйте s к sum так sum+=s; Осталось догадаться где эту строчку воткнуть (тут уж зависит от того как четко вы понимаете порядок работы всей программы и что за чем идёт)
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 19:31 [ТС] |
9 |
|
Laborant666, а выводить в итоге …(sum + s)? до 21 00
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 19:33 |
10 |
|
nonameprogger, нет, выводить в итоге будете sum. Потому что в первый раз у вас sum = 0; Строка посчиталась (в определенном цикле). Получилось s = 3 (например). Вот тут где-то до перехода к следующей строке и до обнуления s (у вас есть там обнуление это s = 0
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 19:46 |
11 |
|
nonameprogger, давайте ещё полчасика на ваши рассуждения, а потом я покажу вам работающий код, если не получится и будем разбираться как он работает. Но не переставайте стараться! Миниатюры
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 19:59 [ТС] |
12 |
|
Laborant666, я сделал. Миниатюры
0 |
|
Laborant666 84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
||||
|
14.01.2021, 20:07 |
13 |
|||
|
Решениеnonameprogger, отлично. Код в студию) Добавлено через 11 секунд Добавлено через 24 секунды
Добавлено через 3 минуты
1 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 20:07 [ТС] |
14 |
|
Laborant666, спасибо за помощь!)
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 20:10 |
15 |
|
nonameprogger, фейсбуку такой код зачем?) Добавлено через 1 минуту
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 20:14 |
16 |
|
Забавная штука конечно. Миниатюры
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 20:19 [ТС] |
17 |
|
Laborant666, «а не строк» и как теперь быть?я думал что я считаю строки пхаха
0 |
|
Spectrages 18 / 14 / 4 Регистрация: 07.01.2019 Сообщений: 67 |
||||
|
14.01.2021, 20:21 |
18 |
|||
|
Не совсем понятно, для чего вы использовали третий цикл, у меня всё и так работает Кликните здесь для просмотра всего текста
0 |
|
1 / 1 / 0 Регистрация: 15.02.2018 Сообщений: 183 |
|
|
14.01.2021, 20:23 [ТС] |
19 |
|
Spectrages, а как сделать чтобы по каждой строке сумму считала?
0 |
|
84 / 74 / 15 Регистрация: 30.06.2020 Сообщений: 724 |
|
|
14.01.2021, 20:28 |
20 |
|
nonameprogger, скажите зачем фейсбуку код, который они сами написать в силах (раз нуб, как я, его смог написать) и я вам расскажу)
0 |
Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.
В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы «Матрицы. Виды матриц. Основные термины».
Содержание темы:
- Сложение и вычитание матриц.
- Умножение матрицы на число.
- Произведение двух матриц.
- Транспонированная матрица.
- Некоторые свойства операций над матрицами.
- Возведение матрицы в степень.
Сложение и вычитание матриц.
Суммой $A+B$ матриц $A_{mtimes n}=(a_{ij})$ и $B_{mtimes n}=(b_{ij})$ называется матрица $C_{mtimes n}=(c_{ij})$, где $c_{ij}=a_{ij}+b_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Аналогичное определение вводят и для разности матриц:
Разностью $A-B$ матриц $A_{mtimes n}=(a_{ij})$ и $B_{mtimes n}=(b_{ij})$ называется матрица $C_{mtimes n}=(c_{ij})$, где $c_{ij}=a_{ij}-b_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Пояснение к записи $i=overline{1,m}$: показатьскрыть
Стоит обратить внимание, что операции сложения и вычитания определены только для матриц одинакового размера. Вообще, сложение и вычитание матриц – операции, ясные интуитивно, ибо означают они, по сути, всего лишь суммирование или вычитание соответствующих элементов.
Пример №1
Заданы три матрицы:
$$
A=left(begin{array} {ccc} -1 & -2 & 1 \
5 & 9 & -8
end{array} right);;
B=left(begin{array} {ccc} 10 & -25 & 98 \
3 & 0 & -14
end{array} right); ;; F=left(begin{array} {cc} 1 & 0 \
-5 & 4
end{array} right).
$$
Можно ли найти матрицу $A+F$? Найти матрицы $C$ и $D$, если $C=A+B$ и $D=A-B$.
Решение
Матрица $A$ содержит 2 строки и 3 столбца (иными словами – размер матрицы $A$ равен $2times 3$), а матрица $F$ содержит 2 строки и 2 столбца. Размеры матрицы $A$ и $F$ не совпадают, поэтому сложить их мы не можем, т.е. операция $A+F$ для данных матриц не определена.
Размеры матриц $A$ и $B$ совпадают, т.е. данные матрицы содержат равное количество строк и столбцов, поэтому к ним применима операция сложения.
$$
C=A+B=left(begin{array} {ccc}
-1 & -2 & 1 \
5 & 9 & -8
end{array} right)+
left(begin{array} {ccc}
10 & -25 & 98 \
3 & 0 & -14
end{array} right)=\=
left(begin{array} {ccc}
-1+10 & -2+(-25) & 1+98 \
5+3 & 9+0 & -8+(-14)
end{array} right)=
left(begin{array} {ccc}
9 & -27 & 99 \
8 & 9 & -22
end{array} right)
$$
Найдем матрицу $D=A-B$:
$$
D=A-B=left(begin{array} {ccc}
-1 & -2 & 1 \
5 & 9 & -8
end{array} right)-
left(begin{array} {ccc}
10 & -25 & 98 \
3 & 0 & -14
end{array} right)=\=
left(begin{array} {ccc}
-1-10 & -2-(-25) & 1-98 \
5-3 & 9-0 & -8-(-14)
end{array} right)=
left(begin{array} {ccc}
-11 & 23 & -97 \
2 & 9 & 6
end{array} right)
$$
Ответ: $C=left(begin{array} {ccc}
9 & -27 & 99 \
8 & 9 & -22
end{array} right)$, $D=left(begin{array} {ccc}
-11 & 23 & -97 \
2 & 9 & 6
end{array} right)$.
Умножение матрицы на число.
Произведением матрицы $A_{mtimes n}=(a_{ij})$ на число $alpha$ называется матрица $B_{mtimes n}=(b_{ij})$, где $b_{ij}=alphacdot a_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.
Пример №2
Задана матрица: $
A=left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)$. Найти матрицы $3cdot A$, $-5cdot A$ и $-A$.
Решение
$$
3cdot A=3cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)
=left(begin{array} {ccc} 3cdot(-1) & 3cdot(-2) & 3cdot 7 \ 3cdot 4 & 3cdot 9 & 3cdot 0 end{array} right)=
left(begin{array} {ccc} -3 & -6 & 21 \ 12& 27 & 0 end{array} right).\
-5cdot A=-5cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)
=left(begin{array} {ccc} -5cdot(-1) & -5cdot(-2) & -5cdot 7 \ -5cdot 4 & -5cdot 9 & -5cdot 0 end{array} right)=
left(begin{array} {ccc} 5 & 10 & -35 \ -20 & -45 & 0 end{array} right).
$$
Запись $-A$ есть сокращенная запись для $-1cdot A$. Т.е., чтобы найти $-A$ нужно все элементы матрицы $A$ умножить на (-1). По сути, это означает, что знак всех элементов матрицы $A$ изменится на противоположный:
$$
-A=-1cdot A=-1cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)=
left(begin{array} {ccc} 1 & 2 & -7 \ -4 & -9 & 0 end{array} right)
$$
Ответ:
$3cdot A=left(begin{array} {ccc} -3 & -6 & 21 \ 12& 27 & 0 end{array} right)$;
$-5cdot A=left(begin{array} {ccc} 5 & 10 & -35 \ -20 & -45 & 0 end{array} right)$;
$-A=left(begin{array} {ccc} 1 & 2 & -7 \ -4 & -9 & 0 end{array} right)$.
Произведение двух матриц.
Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.
Произведением матрицы $A_{mtimes n}=(a_{ij})$ на матрицу $B_{ntimes k}=(b_{ij})$ называется матрица $C_{mtimes k}=(c_{ij})$, для которой каждый элемент $c_{ij}$ равен сумме произведений соответствующих элементов i-й строки матрицы $A$ на элементы j-го столбца матрицы $B$:
$$c_{ij}=sumlimits_{p=1}^{n}a_{ip}b_{pj}, ;; i=overline{1,m}, j=overline{1,n}.$$
Пошагово умножение матриц разберем на примере. Однако сразу стоит обратить внимание, что перемножать можно не все матрицы. Если мы хотим умножить матрицу $A$ на матрицу $B$, то сперва нужно убедиться, что количество столбцов матрицы $A$ равно количеству строк матрицы $B$ (такие матрицы часто называют согласованными). Например, матрицу $A_{5times 4}$ (матрица содержит 5 строк и 4 столбца), нельзя умножать на матрицу $F_{9times 8}$ (9 строк и 8 столбцов), так как количество столбцов матрицы $A$ не равно количеству строк матрицы $F$, т.е. $4neq 9$. А вот умножить матрицу $A_{5times 4}$ на матрицу $B_{4times 9}$ можно, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. При этом результатом умножения матриц $A_{5times 4}$ и $B_{4times 9}$ будет матрица $C_{5times 9}$, содержащая 5 строк и 9 столбцов:
Пример №3
Заданы матрицы:
$
A=left(begin{array} {cccc}
-1 & 2 & -3 & 0 \
5 & 4 & -2 & 1 \
-8 & 11 & -10 & -5
end{array} right)$ и
$
B=left(begin{array} {cc}
-9 & 3 \
6 & 20 \
7 & 0 \
12 & -4
end{array} right)$. Найти матрицу $C=Acdot B$.
Решение
Для начала сразу определим размер матрицы $C$. Так как матрица $A$ имеет размер $3times 4$, а матрица $B$ имеет размер $4times 2$, то размер матрицы $C$ таков: $3times 2$:
Итак, в результате произведения матриц $A$ и $B$ мы должны получить матрицу $C$, состоящую из трёх строк и двух столбцов:
$
C=left(begin{array} {cc}
c_{11} & c_{12} \
c_{21} & c_{22} \
c_{31} & c_{32}
end{array} right)$. Если обозначения элементов вызывают вопросы, то можно глянуть предыдущую тему: «Матрицы. Виды матриц. Основные термины», в начале которой поясняется обозначение элементов матрицы. Наша цель: найти значения всех элементов матрицы $C$.
Начнем с элемента $c_{11}$. Чтобы получить элемент $c_{11}$ нужно найти сумму произведений элементов первой строки матрицы $A$ и первого столбца матрицы $B$:
Чтобы найти сам элемент $c_{11}$ нужно перемножить элементы первой строки матрицы $A$ на соответствующие элементы первого столбца матрицы $B$, т.е. первый элемент на первый, второй на второй, третий на третий, четвертый на четвертый. Полученные результаты суммируем:
$$
c_{11}=-1cdot (-9)+2cdot 6+(-3)cdot 7 + 0cdot 12=0.
$$
Продолжим решение и найдем $c_{12}$. Для этого придётся перемножить элементы первой строки матрицы $A$ и второго столбца матрицы $B$:
Аналогично предыдущему, имеем:
$$
c_{12}=-1cdot 3+2cdot 20+(-3)cdot 0 + 0cdot (-4)=37.
$$
Все элементы первой строки матрицы $C$ найдены. Переходим ко второй строке, которую начинает элемент $c_{21}$. Чтобы его найти придётся перемножить элементы второй строки матрицы $A$ и первого столбца матрицы $B$:
$$
c_{21}=5cdot (-9)+4cdot 6+(-2)cdot 7 + 1cdot 12=-23.
$$
Следующий элемент $c_{22}$ находим, перемножая элементы второй строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:
$$
c_{22}=5cdot 3+4cdot 20+(-2)cdot 0 + 1cdot (-4)=91.
$$
Чтобы найти $c_{31}$ перемножим элементы третьей строки матрицы $A$ на элементы первого столбца матрицы $B$:
$$
c_{31}=-8cdot (-9)+11cdot 6+(-10)cdot 7 + (-5)cdot 12=8.
$$
И, наконец, для нахождения элемента $c_{32}$ придется перемножить элементы третьей строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:
$$
c_{32}=-8cdot 3+11cdot 20+(-10)cdot 0 + (-5)cdot (-4)=216.
$$
Все элементы матрицы $C$ найдены, осталось лишь записать, что $C=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right)$. Или, если уж писать полностью:
$$
C=Acdot B =left(begin{array} {cccc}
-1 & 2 & -3 & 0 \
5 & 4 & -2 & 1 \
-8 & 11 & -10 & -5
end{array} right)cdot left(begin{array} {cc}
-9 & 3 \
6 & 20 \
7 & 0 \
12 & -4
end{array} right)=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right).
$$
Ответ: $C=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right)$.
Кстати сказать, зачастую нет резона расписывать подробно нахождение каждого элемента матрицы-результата. Для матриц, размер которых невелик, можно поступать и так:
$$
left(begin{array} {cc}
6 & 3 \
-17 & -2
end{array}right)cdot
left(begin{array} {cc}
4 & 9 \
-6 & 90
end{array} right)
=left(begin{array} {cc}
6cdot{4}+3cdot(-6) & 6cdot{9}+3cdot{90} \
-17cdot{4}+(-2)cdot(-6) & -17cdot{9}+(-2)cdot{90}
end{array} right)
=left(begin{array} {cc}
6 & 324 \
-56 & -333
end{array} right)
$$
Стоит также обратить внимание, что умножение матриц некоммутативно. Это означает, что в общем случае $Acdot Bneq Bcdot A$. Лишь для некоторых типов матриц, которые именуют перестановочными (или коммутирующими), верно равенство $Acdot B=Bcdot A$. Именно исходя из некоммутативности умножения, требуется указывать как именно мы домножаем выражение на ту или иную матрицу: справа или слева. Например, фраза «домножим обе части равенства $3E-F=Y$ на матрицу $A$ справа» означает, что требуется получить такое равенство: $(3E-F)cdot A=Ycdot A$.
Транспонированная матрица.
Транспонированной по отношению к матрице $A_{mtimes n}=(a_{ij})$ называется матрица $A_{ntimes m}^{T}=(a_{ij}^{T})$, для элементов которой $a_{ij}^{T}=a_{ji}$.
Попросту говоря, для того, чтобы получить транспонированную матрицу $A^T$, нужно в исходной матрице $A$ заменить столбцы соответствующими строками по такому принципу: была первая строка – станет первый столбец; была вторая строка – станет второй столбец; была третья строка – станет третий столбец и так далее. Например, найдем транспонированную матрицу к матрице $A_{3times 5}$:
Соответственно, если исходная матрица имела размер $3times 5$, то транспонированная матрица имеет размер $5times 3$.
Некоторые свойства операций над матрицами.
Здесь предполагается, что $alpha$, $beta$ – некоторые числа, а $A$, $B$, $C$ – матрицы. Для первых четырех свойств я указал названия, остальные можно назвать по аналогии с первыми четырьмя.
- $A+B=B+A$ (коммутативность сложения)
- $A+(B+C)=(A+B)+C$ (ассоциативность сложения)
- $(alpha+beta)cdot A=alpha A+beta A$ (дистрибутивность умножения на матрицу относительно сложения чисел)
- $alphacdot(A+B)=alpha A+alpha B$ (дистрибутивность умножения на число относительно сложения матриц)
- $A(BC)=(AB)C$
- $(alphabeta)A=alpha(beta A)$
- $Acdot (B+C)=AB+AC$, $(B+C)cdot A=BA+CA$.
- $Acdot E=A$, $Ecdot A=A$, где $E$ – единичная матрица соответствующего порядка.
- $Acdot O=O$, $Ocdot A=O$, где $O$ – нулевая матрица соответствующего размера.
- $left(A^T right)^T=A$
- $(A+B)^T=A^T+B^T$
- $(AB)^T=B^Tcdot A^T$
- $left(alpha A right)^T=alpha A^T$
В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
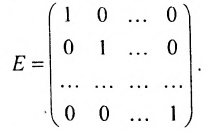
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 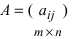
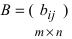
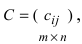
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 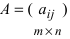
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 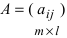
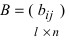
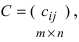
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 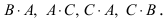
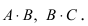
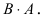
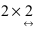
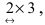
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
Определение: Обратной матрицей к исходной квадратной матрице 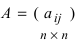
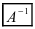
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 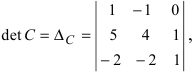
Вычислим алгебраические дополнения всех элементов определителя: 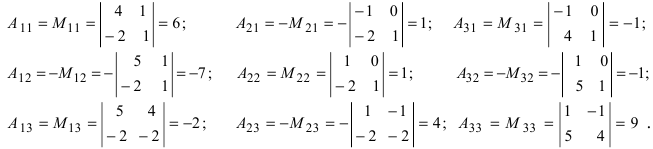
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 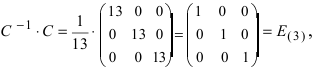
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 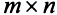
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 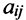
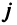
Например, матрица
или, в сокращенной записи,
Например, 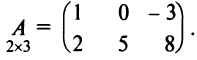
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 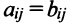
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 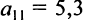
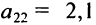
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 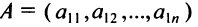
Матрица называется квадратной 
Например, 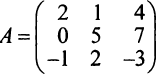
Элементы матрицы 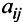
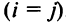
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
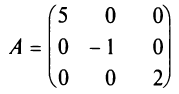
Если у диагональной матрицы 

Например,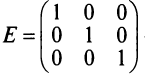
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 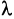
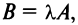
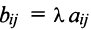
Например, если 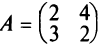
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
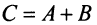
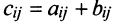
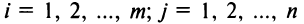
Например,
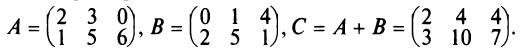
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй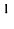
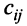

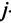
Пример №1
Вычислить произведение матриц 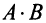
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 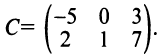
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
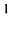
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 
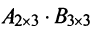
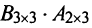
б)Если даже произведения 

Пример №2
Найти произведения матриц 

Решение:
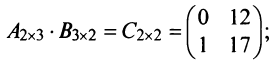
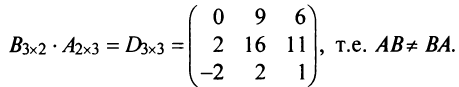


Пример №3
Найти произведения матриц 

Решение:
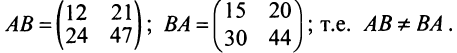
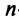
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 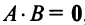
Возведение в степень
Целой положительной степенью 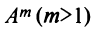
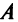
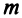

Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 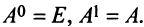
Пример №4
Найти 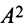
Решение:
Обращаем внимание на то, что из равенства 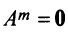
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 



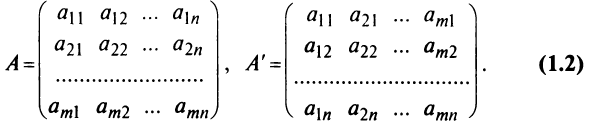

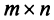

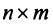
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 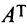
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 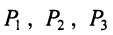
где каждый элемент 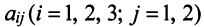
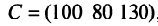
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 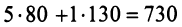
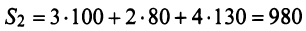
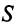
Тогда общая стоимость сырья 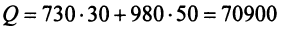
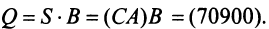
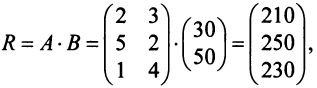
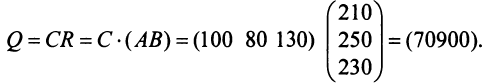
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 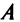
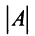
Определителем матрицы первого порядка 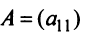
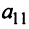
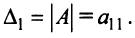
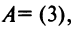
Определителем матрицы второго порядка 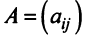
Произведения а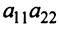
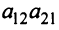
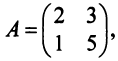
Пусть дана квадратная матрица третьего порядка: 
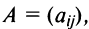
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
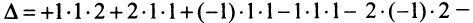
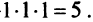
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 
Из общего числа 
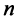
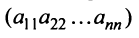
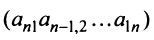
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 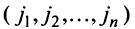
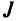
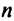

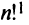
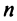
Введем понятие беспорядка, или инверсии, в перестановке 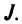
Возвращаясь к наборам (1.5) из элементов матрицы 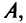
и число 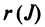
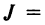
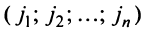
Определение. Определителем квадратной матрицы 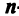
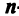
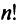
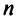
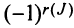
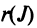
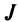
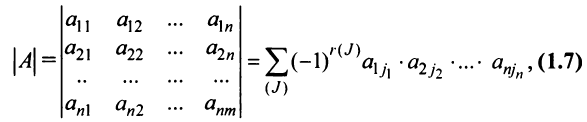
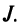
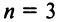
то же число, что и по формуле (1.4).
Заметим, что с ростом 
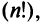
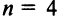
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 

Минором 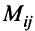
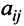

определитель матрицы 

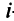
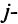
Например, минором элемента 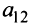

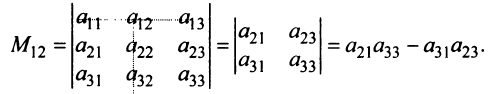

Алгебраическим дополнением 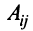
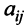

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца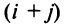
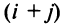
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
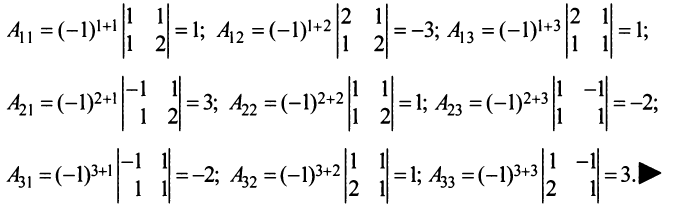
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
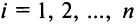
(разложение по элементам 
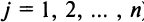

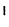
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы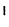
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 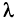

Пусть определитель исходной матрицы равен 

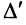
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 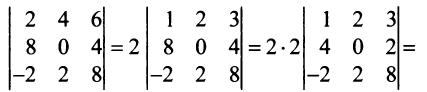
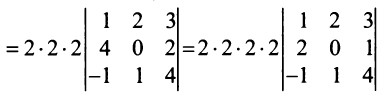
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: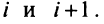


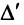
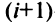
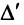
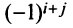
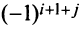
Если переставить не соседние строки, а, скажем, 
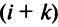

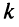
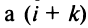
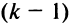
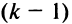
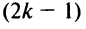
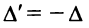
Доказательство для столбцов аналогично.
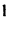
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.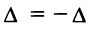
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 
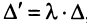

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 
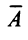



т.е. матрица 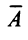

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
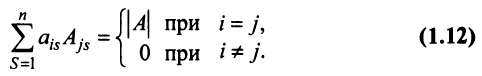
Пусть для определенности к элементам 

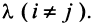
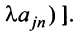

где 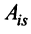

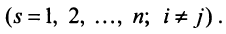
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 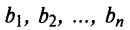
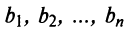
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 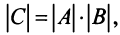
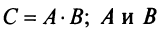
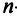
Замечание. Из свойства 10 следует, что даже если 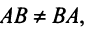
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа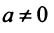
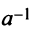
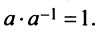
Определение. Матрица 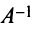

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 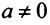
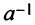

Если определитель матрицы отличен от нуля 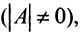
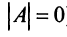
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 

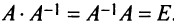
Достаточность. Пусть 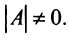
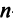
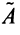


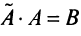
Аналогично доказывается, что произведение 
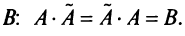
то произведения 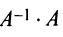
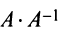
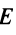
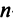
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 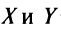
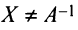
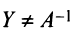

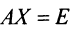
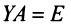

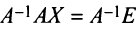
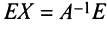
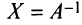

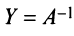
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы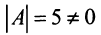


2°. Находим матрицу 

3°. Находим алгебраические дополнения элементов матрицы 
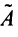
4° . Вычисляем обратную матрицу
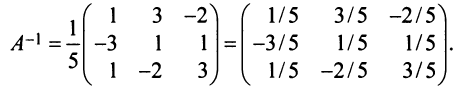
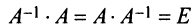
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
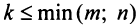
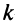

Например, из матрицы 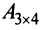
Определение. Рангом матрицы 
Ранг матрицы 
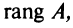
Из определения следует: а) ранг матрицы 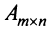
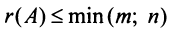
б) 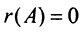
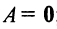
в) для квадратной матрицы 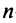
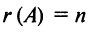

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
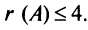
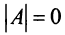

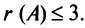
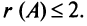
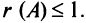

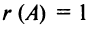
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 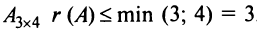
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,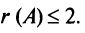
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
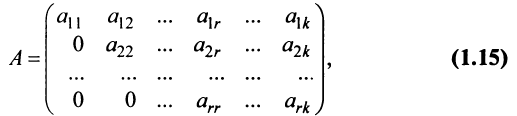
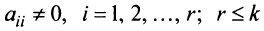
Замечание. Условие 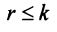
Очевидно, что ранг ступенчатой матрицы равен 
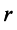
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 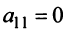
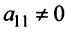
2°. Если 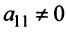
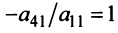
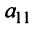
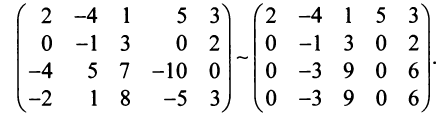
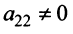
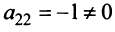
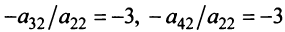
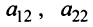
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
Для рангов матриц справедливы следующие соотношения:
5)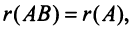

6) 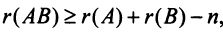
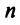


Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.


Две строки матрицы называются равными, если равны их соответствующие элементы: 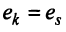
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 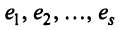
где 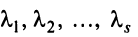
Строки матрицы 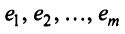
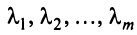
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

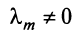
где
Таким образом, строка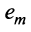
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 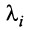
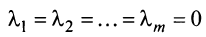
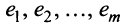
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


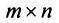
Это означает, что существует отличный от нуля минор 

Тогда строки матрицы 
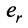
Вычтем из элементов 
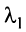
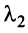
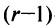
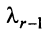

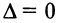

Строки 
Покажем, что любые 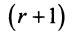
Рассмотрим минор 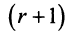
при дополнении рассматриваемого минора элементами еще одной строки 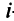
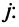
Этот минор равен нулю, так как ранг матрицы равен 
Раскладывая его по элементам последнего (добавленного) столбца, получаем 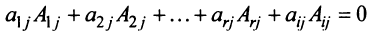
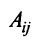

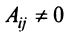
Разделив последнее равенство на 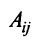
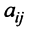
где
Фиксируем значение 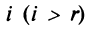

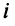
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
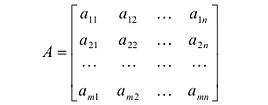
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 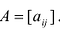
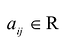
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 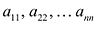
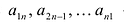
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 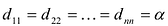
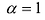
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 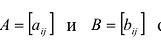
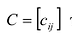
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 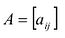
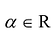
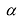
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 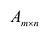
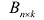
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 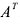
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 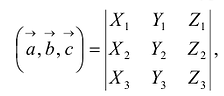
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 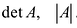
Минором 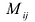

Пример №14
Найти минор 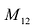
По определению, минор 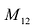
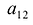
Алгебраическим дополнением элемента 
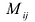
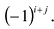

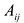
Пример №15
Найти алгебраическое дополнение элемента 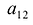
Определителем квадратной матрицы А n-го порядка 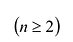
где аи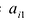
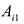
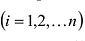
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 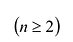
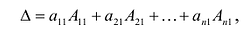
где 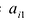
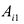
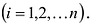
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
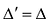
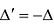
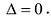
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
Умножим элементы i-той строки на 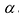
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 
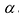
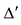


Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 


Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 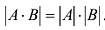
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 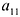
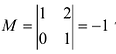
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 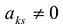
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 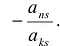
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 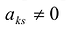
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 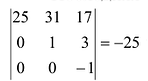
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 
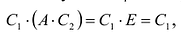
Откуда 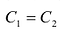

Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 
Пусть А имеет обратную матрицу. Тогда 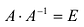
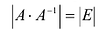
Следовательно, 
Пусть 

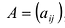
здесь 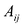
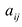
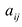
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 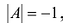

Матрицу 
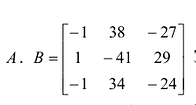
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 
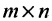
Числа 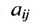
Матрицы удобно обозначать в виде 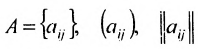
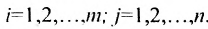
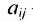
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
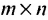
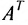
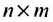
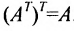
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 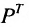
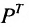
Если, элементы 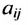
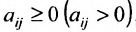
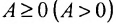
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 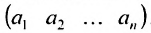
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом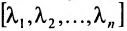
Если в диагональной матрице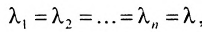
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 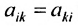
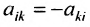
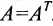
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 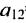
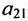
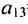
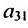
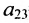
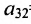
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 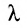
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 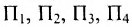
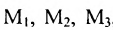
где 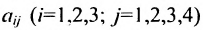
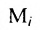
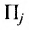
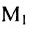
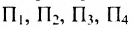
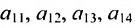
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 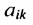
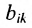
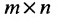
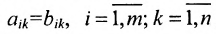
Определение 3.2.1. Суммой матриц А а В размерности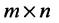
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 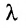
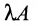
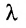
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 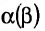
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 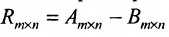
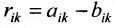
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 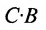
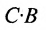
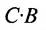
Аналогичным образом определяется произведение матрицы-строки 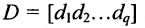
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 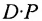
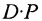
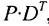
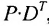
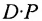
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =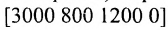
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 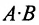
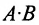
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 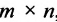
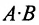
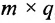
Определение 3.2.4. Произведением матрицы А размерности 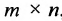
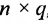
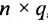
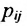
, при 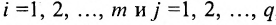
- Заказать решение задач по высшей математике
Пример №22
Пусть 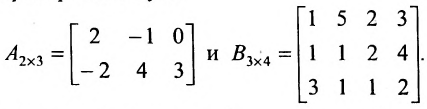
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 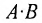
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 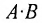
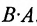
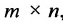
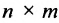
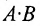
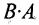
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 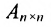
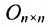
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 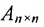
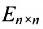
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 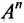
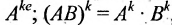
Значением многочлена
с числовыми коэффициентами 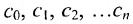
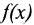
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 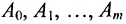
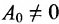
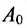
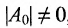
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 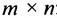
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
Пример №24
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
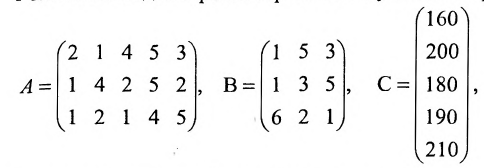
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

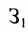
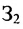
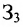
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 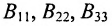
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 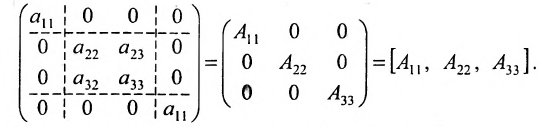
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 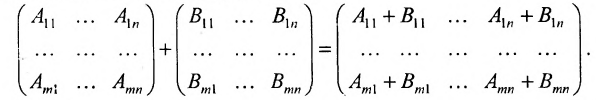
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 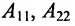
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или
суммирования служит заглавная греческая буква 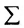
например, сумму 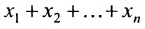
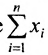
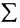
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 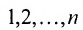
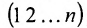
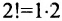
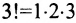
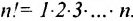
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 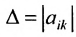
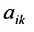
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 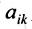
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 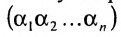
В частности, определителем второго порядка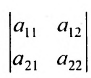
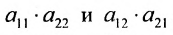
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 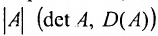
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
Доказательство. Рассмотрим определитель 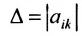
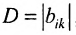
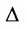
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 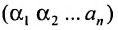
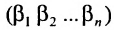
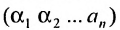
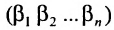
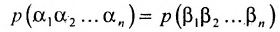
Так как 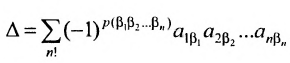
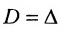
Из свойства 
Доказательство. Рассмотрим определитель 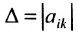
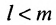
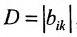

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 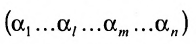
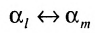
Затем поменяем местами сомножители 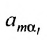
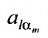
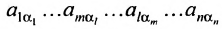
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 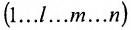
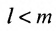
вторых индексов такая же, как и в выражении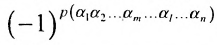
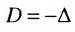
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 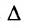
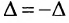
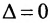
Доказательство. Пусть в определителе 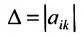
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 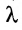
Из свойства 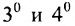
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 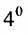
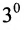
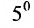
Доказательство. Пусть все элементы 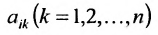

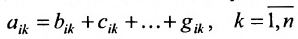
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
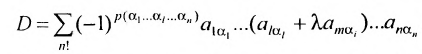
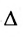
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 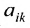

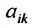
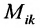
Определение 3.8.1. Минор 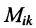
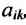
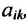

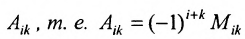
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 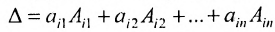
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 
Определитель 
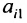
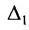

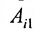
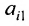
Следовательно,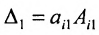
Аналогично 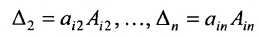
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
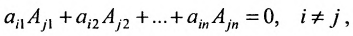
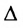
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 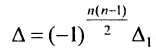
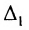
3) Если определитель 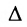
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
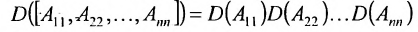
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
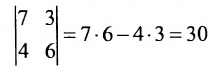
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 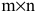
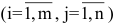
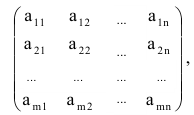
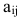
Например, элемент 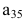
Суммой двух матриц одинакового размера 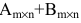
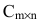
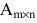
Например,
Произведением матрицы 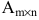
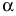
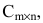
Например,
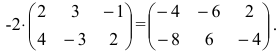
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 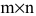
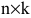
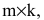
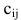
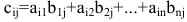
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 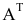
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Теорема
Кронекера — Капелли: Система
линейных алгебраических уравнений
совместна тогда и только тогда, когда
ранг её основной матрицы равен рангу
её расширенной матрицы. В частности:
-
Количество
главных переменных системы равно рангу
системы. -
Совместная
система будет определена (её решение
единственно), если ранг системы равен
числу всех её переменных.
7
Системы линейных алгебраических
уравнений? Метод Гауса?
Система m линейных
алгебраических
уравнений с n неизвестными (или, линейная
система,
также употребляется аббревиатура СЛА́У)
в линейной
алгебре —
это система уравнений вида
|
|
Здесь
—
количество уравнений, а
—
количество неизвестных. x1, x2,
…, xn —
неизвестные, которые надо определить. a11, a12,
…, amn —
коэффициенты системы — и b1, b2,
… bm —
свободные члены — предполагаются
известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно[2].
Система
линейных уравнений может быть
представлена в
матричной форме как:
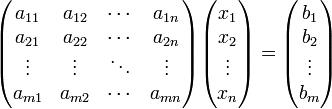
или:
.
Здесь
—
это матрица системы,
—
столбец неизвестных, а
—
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
Системы
линейных уравнений называются эквивалентными,
если множество их решений совпадает,
то есть любое решение одной системы
одновременно является решением другой,
и наоборот.
Систему,
эквивалентную данной, можно получить,
в частности, заменив одно из уравнений
на это уравнение, умноженное на любое
отличное от нуля число. Эквивалентную
систему можно получить также, заменив
одно из уравнений суммой этого уравнения
с другим уравнением системы. В общем,
замена уравнения системы на линейную
комбинацию уравнений даёт систему,
эквивалентную исходной.
Система
линейных алгебраических уравнений
эквивалентна
системе
,
где
— невырожденная
матрица.
В
частности, если сама матрица
—
невырожденная, и для неё существует обратная
матрица
,
то решение системы уравнений можно
формально записать в виде
.
Ме́тод
Га́усса[1] —
классический метод решения системы
линейных алгебраических уравнений (СЛАУ).
Это метод последовательного
исключения переменных,
когда с помощью элементарных преобразований
система уравнений приводится к
равносильной системе ступенчатого (или
треугольного) вида, из которой
последовательно, начиная с последних
(по номеру) переменных, находятся все
остальные переменные[2].
Описание
Алгоритм
решения СЛАУ методом
Гаусса подразделяется на два этапа.
-
На
первом этапе осуществляется так
называемый прямой ход, когда
путём элементарных
преобразований над
строками систему приводят к ступенчатой
или треугольной
форме,
либо устанавливают, что система
несовместна. А именно, среди элементов
первого столбца матрицы выбирают
ненулевой, перемещают его на крайнее
верхнее положение перестановкой строк
и вычитают получившуюся после перестановки
первую строку из остальных строк,
домножив её на величину, равную отношению
первого элемента каждой из этих строк
к первому элементу первой строки,
обнуляя тем самым столбец под ним. После
того, как указанные преобразования
были совершены, первую строку и первый
столбец мысленно вычёркивают и продолжают
пока не останется матрица нулевого
размера. Если на какой-то из итераций
среди элементов первого столбца не
нашёлся ненулевой, то переходят к
следующему столбцу и проделывают
аналогичную операцию. -
На
втором этапе осуществляется так
называемый обратный ход, суть которого
заключается в том, чтобы выразить все
получившиеся базисные переменные через
небазисные и построить фундаментальную
систему решений,
либо, если все переменные являются
базисными, то выразить в численном виде
единственное решение системы линейных
уравнений. Эта процедура начинается с
последнего уравнения, из которого
выражают соответствующую базисную
переменную (а она там всего одна) и
подставляют в предыдущие уравнения, и
так далее, поднимаясь по -
«ступенькам»
наверх. Каждой строчке соответствует
ровно одна базисная переменная, поэтому
на каждом шаге, кроме последнего (самого
верхнего), ситуация в точности повторяет
случай последней строки.
Гаусса
требует порядка
действий.
Этот
Метод метод опирается на:
Теорема
(о приведении матриц к ступенчатому
виду).
Любую
матрицу путём элементарных преобразований
только над строками можно привести к
ступенчатому виду.
Пример
Покажем,
как методом Гаусса можно решить следующую
систему:
Обнулим
коэффициенты при
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
и
,
соответственно:
Теперь
обнулим коэффициент при
в
третьей строке, вычтя из неё вторую
строку, умноженную на
:

В
результате мы привели исходную систему
к треугольному
виду,
тем самым закончив первый этап алгоритма.
На
втором этапе разрешим полученные
уравнения в обратном порядке. Имеем:
из
третьего;
из
второго, подставив полученное
из
первого, подставив полученные
и
.
Таким
образом исходная система решена.
Достоинства метода
-
Менее
трудоёмкий по сравнению с другими
методами. -
Позволяет
однозначно установить, совместна
система или нет, и если совместна, найти
её решение. -
Позволяет
найти максимальное число линейно
независимых уравнений — ранг
матрицы системы[
8
Теорема Кронекера-Капелли
Теоре́ма
Кро́некера — Капе́лли —
критерий совместности системы линейных
алгебраических уравнений:Система
линейных алгебраических
уравнений совместна тогда
и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если ранг
равен числу неизвестных, и бесконечное
множество решений, если ранг меньше
числа неизвестных
Необходимость.Пусть система совместна.
Тогда существуют числа
такие,
что
.
Следовательно, столбец
является
линейной комбинацией столбцов
матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
.
Достаточность
Пусть
.
Возьмем в матрице
какой-нибудь
базисный минор. Так как
,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о
базисном миноре последний
столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
Следствия
-
Количество
главных переменных системы равно
рангу системы. -
Совместная система будет
определена (её решение единственно),
если ранг системы равен числу всех её
переменных. -
Решить
с помощью теоремы Кронекера-Капелли
систему уравнений:
Решение
Из последнего преобразования вытекает,
что
.
Начальная система эквивалентна
системе:
.
Среди миноров второго порядка,
составленных из элементов матрицы
коэффициентов при неизвестных, существует
хотя бы один отличный от нуля. В нашем
случае их несколько. Если отличный от
нуля минор выберем из коэффициентов
при двух неизвестных, то таким образом
мы переведем эти неизвестные в разряд
основных. Пусть, например, это неизвестные
х1,
х2.
Тогда, перенеся остальные неизвестные
в правую часть системы уравнений,
получим:
.
Главный определитель этой системы
.
Найдем
.
.
По правилу Крамера
Последние равенства определяют общее
решение системы уравнений. Чтобы
получить частные решения, достаточно
предоставить свободным неизвестным
х3,
х4,
х5 некоторых
числовых значений.
Например, если
х3 =
0, х4 =
0, х5 =
0,
имеем решение
;
если х3 =
2, х4 =
1, х5 =
–2 — решение (3, 5, 2, 1, –2) и т.д.
Таких частных решений в данном случае
можно построить бесконечное количество. -
9
Определители. Свойства определителей?
Определи́тель (или детермина́нт) —
одно из основных понятий линейной
алгебры.
Определитель матрицы является многочленом от
элементов квадратной матрицы (то есть
такой, у которой количество строк и
столбцов равно). В общем случае матрица может
быть определена над любым
коммутативным кольцом,
в этом случае определитель будет
элементом того же кольца.
Определитель матрицы А обозначается
как: det(A), |А| или Δ(A).
Для
матрицы первого порядка детерминантом является
сам единственный элемент этой матрицы:
Для
матрицы
детерминант
определяется как
Для
матрицы
определитель
задаётся рекурсивно:
,
где
— дополнительный
минор к
элементу
.
Эта формула называется разложением
по строке.
В
частности, формула вычисления определителя
матрицы
такова:
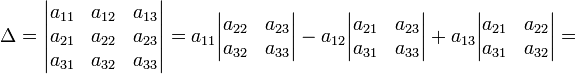
Легко
доказать, что при транспонировании определитель
матрицы не изменяется (иными словами,
аналогичное разложение по первому
столбцу также справедливо, то есть даёт
такой же результат, как и разложение по
первой строке):
Свойства определителей
-
Определитель — кососимметричная полилинейная
функция строк (столбцов) матрицы.
Полилинейность означает, что определитель
линеен по всем строкам (столбцам):
,
где
и т. д. —
строчки матрицы,
—
определитель такой матрицы. -
При
добавлении к любой строке (столбцу) линейной
комбинации других
строк (столбцов) определитель не
изменится. -
Если
две строки (столбца) матрицы совпадают,
то её определитель равен нулю. -
Если
две (или несколько) строки (столбца)
матрицы линейно зависимы, то её
определитель равен нулю. -
Если
переставить две строки (столбца) матрицы,
то её определитель умножается на (-1). -
Общий
множитель элементов какого-либо ряда
определителя можно вынести за знак
определителя. -
Если
хотя бы одна строка (столбец) матрицы
нулевая, то определитель равен нулю. -
Сумма
произведений всех элементов любой
строки на их алгебраические
дополнения равна
определителю. -
Сумма
произведений всех элементов любого
ряда на алгебраические
дополнения соответствующих
элементов параллельного ряда равна
нулю. -
Определитель
произведения квадратных матриц
одинакового порядка равен произведению
их определителей (cм. также формулу
Бине-Коши). -
С
использованием индексной
нотации определитель
матрицы 3×3 может быть определён с
помощью символа
Леви-Чивита из
соотношения: -
1.
Определитель не меняется при
транспонировании. -
2.
Если одна из строк определителя состоит
из нулей, то определитель равен нулю. -
3.
Если в определителе переставить две
строки, определитель поменяет знак. -
4.
Определитель, содержащий две одинаковые
строки, равен нулю. -
5.
Если все элементы некоторой строки
определителя умножить на некоторое
число k, то сам определитель умножится
на k. -
6.
Определитель, содержащий две
пропорциональные строки, равен нулю.
10. Теорема о разложении определителей по строкам, по столбцам:
Теоре́ма
Лапла́са —
одна из теорем линейной
алгебры.
Названа в честь французского
математика Пьера-Симона
Лапласа (1749
— 1827), которому приписывают создание
этой теоремы в 1772 году[1],
хотя частный случай этой теоремы о
разложении определителя по строке
(столбцу) был известен ещё Лейбницу.
Формулировка
Для
начала, введём несколько определений.
Пусть
— матрица размера
,
и пусть выбраны любые
строк
матрицы
с
номерами
и
любые
столбцов
с номерами
.
Определитель матрицы,
получаемой из
вычеркиванием
всех строк и столбцов, кроме выбранных,
называется минором
-го
порядка, расположенным в строках с
номерами
и
столбцах с номерами
.
Он обозначается следующим образом:

А
определитель матрицы, получаемой
вычеркиванием только выбранных строк
и столбцов из квадратной матрицы,
называется дополнительным
минором к
минору
:

где
и
—
номера невыбранных строк и стобцов.
Алгебраическое
дополнение минора
определяется
следующим образом:
где
,
.
Справедливо
следующее утверждение.
Теорема
Лапласа
Пусть
выбраны любые
строк
матрицы
.
Тогда определитель матрицы
равен
сумме всевозможных произведений
миноров
-го
порядка, расположенных в этих строках,
на их алгебраические дополнения.
где
суммирование ведётся по всевозможным
номерам столбцов
Число
миноров, по которым берётся сумма в
теореме Лапласа, равно числу способов
выбрать
столбцов
из
,
то есть биномиальному
коэффициенту
.
Так
как строки и столбцы матрицы равносильны
относительно свойств определителя,
теорему Лапласа можно сформулировать
и для столбцов матрицы.
Разложение определителя по строке (столбцу) (Следствие 1)
Широко
известен частный случай теоремы Лапласа —
разложение определителя по строке или
столбцу. Он позволяет
представить определитель квадратной матрицы в
виде суммы произведений элементов любой
её строки или столбца на их алгебраические
дополнения.
Пусть
—
квадратная матрица размера
.
Пусть также задан некоторый номер
строки
либо
номер столбца
матрицы
.
Тогда определитель
может
быть вычислен по следующим формулам:
Разложение
по
-й
строке:

Разложение
по
-му
столбцу:
где
—
алгебраическое дополнение к минору,
расположенному в строке с номером
и
столбце с номером
.
также
называют алгебраическим дополнением
к элементу
.
Утверждение
является частным случаем теоремы
Лапласа. Достаточно в ней положить
равным
1 и выбрать
-ую
строку, тогда минорами, расположенными
в этой строке будут сами элементы.
Следствие 2 (фальшивое разложение определителя)
Сумма
произведений всех элементов некоторой
строки (столбца) матрицы А на алгебраические
дополнения соответствующих элементов
любой другой строки (столбца) равна
нулю.
Доказательство. Рассмотрим
сумму произведений всех элементов
произвольной k-ой строки матрицы А на
алгебраические дополнения соответствующих
элементов любой другой, скажем, i-ой
строки матрицы А. Пусть A′ – матрица, у
которой все строки, кроме i-ой, такие же,
как у матрицы А, а элементами i-ой строки
матрицы A′ являются соответствующие
элементы k-ой строки матрицы А. Тогда у
матрицы A′ две одинаковые строки и,
следовательно, по свойству матрицы об
одинаковых строках имеем, что |A′| = 0 . С
другой стороны, по следствию 1 определитель
|A′| равен сумме произведений всех
элементов i-ой строки матрицы A′ на их
алгебраические дополнения. Заметим,
что алгебраические дополнения элементов
i-ой строки матрицы A′ совпадают с
алгебраическими дополнениями
соответствующих элементов i-ой строки
матрицы А. Но элементами i-ой строки
матрицы A′ являются соответствующие
элементы k-ой строки матри- цы А. Таким
образом, сумма произведений всех
элементов i-ой строки матрицы A′ на их
алгебраические дополнения с одной
стороны равна нулю, а с другой стороны
равна сумме произведений всех элементов
k-ой строки матрицы А на алгебраические
дополнения соответствующих элементов
i-ой строки матрицы А
11. Теорема Крамера
Метод
Крамера (правило Крамера) —
способ решения квадратных систем
линейных алгебраических уравнений с
ненулевым определителем основной
матрицы (причём
для таких уравнений решение существует
и единственно). Назван по имени Габриэля
Крамера (1704–1752),
придумавшего метод.
Описание метода
Для
системы
линейных
уравнений с
неизвестными
(над произвольным полем)

с
определителем матрицы системы
,
отличным от нуля, решение записывается
в виде

(i-ый
столбец матрицы системы заменяется
столбцом свободных членов).
В другой
форме правило Крамера формулируется
так: для любых коэффициентов c1,
c2,
…, cn справедливо
равенство:

В
этой форме формула Крамера справедлива
без предположения, что
отлично
от нуля, не нужно даже, чтобы коэффициенты
системы были бы элементами целостного
кольца (определитель
системы может быть даже делителем нуля
в кольце коэффициентов). Можно также
считать, что либо наборы
и
,
либо набор
состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
Пример
Система
линейных уравнений:
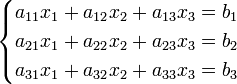
Определители:


Решение:
Пример:

Определители:


Вычислительная сложность
Метод
Крамера требует вычисления
определителей
размерности
.
При использовании метода
Гаусса для
вычисления определителей, метод имеет
временную сложность порядка
,
что хуже, чем если бы метод
Гаусса напрямую
использовался для решения системы
уравнений. Поэтому метод считался
непрактичным. Однако в 2010 году было
показано, что метод Крамера может быть
реализован со сложностью
,
сравнимой со сложностью метода
Гаусса.
12. Теорема о определителях произведении матриц?
Теорема.
Определитель произведения двух матриц
п-го
порядка равен произведению определителей
этих матриц.
Пусть
даны матрицы п-го
порядка
и
и пусть
.
Построим определитель
порядка 2п:
в его верхнем левом углу поставим матрицу
А,
в правом нижнем – матрицу В,
в правом верхнем углу поставим нули, а
на главной диагонали левого нижнего
угла поставим числа –1, заполнив свободные
места нулями. Определитель
будет иметь вид

Применим
к определителю D
теорему Лапласа о разложении по первым
п
строкам.
В результате получим
D = detAdetB
Преобразуем
определитель D
так, чтобы при неизменности его значения
все элементы bij
стали
нулями. Для этого к п+1—му
столбцу прибавим первый столбец,
умноженный на b11,
второй столбец, умноженный на b21
и т. д. К (п + 2)му
столбцу прибавим первый, умноженный на
b12,
второй, умноженный на
b22
и
т. д.
Вообще к (n + j)-столбцу,
где j =1,2,,п,
прибавим сумму первых п
столбцов, умноженных соответственно
на
.
Такие
преобразования привели к тому, что в
правом нижнем углу определителя (будем
называть его по-прежнему D,
так как величина его не изменилась)
оказались только нули. В правом верхнем
углу определителя теперь появятся
числа, определённые следующим образом:
в i—той
строке в столбце с номером n + j
будет стоять сумма
.
Эта сумма, исходя из правила перемножения
матриц, равна элементу матрицы
.
Таким образом, в правом верхнем углу
оказалась матрица С.
Определитель D
принял вид

Применим
теперь разложение определителя
по последним п
столбцам. Дополнительный минор для
минора, стоящего на пересечении первых
п
строк и последних п
столбцов равен (–1)п.
Для самого минора сумма s,
определяемая формулой (*), будет равна

Отсюда
получается:
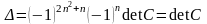
13. Теорема о нахождении обратной матрицы с помощью алгебраической дополнении
Рассмотрим
квадратную матрицу
.
Обозначим =det
A.
Квадратная
матрица А называется невырожденной, или неособенной,
если ее определитель отличен от нуля,
и вырожденной, или особенной,
если =
0.
Квадратная
матрица В называется обратной для
квадратной матрицы А того же порядка,
если их произведение А В = В А = Е, где Е
— единичная матрица того же порядка, что
и матрицы А и В.
Теорема. Для
того, чтобы матрица А имела обратную,
необходимо и достаточно, чтобы ее
определитель был отличен от нуля.
Матрица,
обратная матрице А, обозначается через
А1,
так что В = А1.
Обратная матрица вычисляется по формуле
,
(4.5)
где
А i
j —
алгебраические дополнения элементов
a i
j.
Вычисление
обратной матрицы по формуле (4.5) для
матриц высокого порядка очень трудоемко,
поэтому на практике бывает удобно
находить обратную матрицу с помощью
метода элементарных преобразований
(ЭП). Любую неособенную матрицу А путем
ЭП только столбцов (или только строк)
можно привести к единичной матрице Е.
Если совершенные над матрицей А ЭП в
том же порядке применить к единичной
матрице Е, то в результате получится
обратная матрица. Удобно совершать ЭП
над матрицами А и Е одновременно,
записывая обе матрицы рядом через черту.
Отметим еще раз, что при отыскании
канонического вида матрицы с целью
нахождения ранга
матрицы можно
пользоваться преобразованиями строк
и столбцов. Если нужно найти обратную
матрицу, в процессе преобразований
следует использовать только строки или
только столбцы.
Пример
2.10.
Для матрицы
найти
обратную.
Решение. Находим
сначала детерминант матрицы А
значит,
обратная матрица существует и мы ее
можем найти по формуле:
,
где
Аi
j (i,j=1,2,3)
— алгебраические дополнения элементов
аi
j исходной
матрицы.
Откуда
.
14. Нахождение обратной матрицы с помощью элементарной преобразовании
предположим,
что матрица A
— неособенная и рассмотрим метод
нахождения обратной матрицы, основанный
на элементарных операциях над строками.
В
данном контексте под элементарными
преобразованиями понимается:
-
Умножение
строки на любое ненулевое число. -
Прибавление
к одной строке любой другой, предварительно
умноженной на любое число.
Алгоритм
метода чрезвычайно прост по своей сути.
Сначала
составляется расширенная матрица –
присоединением к матрице A единичной
матрицы E:

Затем
с помощью элементарных операций над
строками расширенная матрица (A | E)
преобразуется к виду (E | B).
С
формальной точки зрения такие
преобразования могут быть реализованы
умножением на матрицу A некоторой
матрицы T,
которая представляет собой произведение
соответствующих элементарных матриц
(матрицы перестановки, матрицы
масштабирования, неунитарной матрицы):
TA
= E.
Это
уравнение означает, что матрица
преобразования T представляет
собой обратную матрицу для матрицы A:
T = A-1.
Тогда
TE = A-1
и, следовательно,
15. Поле комплексных чисел. Алгебраическая формула комплексных чисел
Ко́мпле́ксные[1] чи́сла (устар. Мнимые
числа[2]),
— расширение множества вещественных
чисел,
обычно обозначается
.
Любое комплексное число может быть
представлено как формальная сумма
,
где
и
—
вещественные числа,
— мнимая
единица[3].
Комплексные
числа образуют алгебраически
замкнутое поле —
это означает, что многочлен степени
с
комплексными коэффициентами имеет
ровно
комплексных
корней (основная
теорема алгебры).
Это одна из главных причин широкого
применения комплексных чисел в
математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии,квантовой
механике, теории
колебаний и
многих других.
Поле
комплексных чисел можно понимать
как расширение
поля вещественных
чисел, в котором многочлен
имеет
корень. Следующие две
элементарные модели показывают,
что непротиворечивое построение такой
системы чисел возможно. Оба приведенных
определения приводят к изоморфным расширениям
поля вещественных чисел
,
как и любые другие конструкции поля
разложения многочлена
.
Стандартная
модель
Комплексное
число
можно определить как упорядоченную
пару вещественных чисел
.
Введём операции сложения и умножения
таких пар следующим образом:
Алгебраическая форма
Запись
комплексного числа
в
виде
,
,
называется алгебраической
формой комплексного
числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что
):
Алгебраическое
расширение поля действительных чисел
с
помощью элемента
,
являющегося корнем
многочлена
,
называется полем комплексных чисел1). Поле комплексных чисел обозначается
через
.
Предложение
1. Каждое ассоциативное
коммутативное кольцо
с
единицей и
без делителей
нуля,
являющееся двумерным векторным
пространством над
полем
,
изоморфно полю
.
Теорема
1.(Основная
теорема алгебры.) Поле комплексных чисел
алгебраически
замкнуто.
16.Тригонометрическая
форма комплексных
где r —
модуль;
—
агрумент комплексного числа.
Если
то:
Формула
Муавра
Извлечение
корней из комплексных чисел
Та
запись комплексного числа, которую мы
использовали до сих пор,
называется алгебраической
формой записи комплексного числа.
Часто бывает удобна немного другая
форма записи комплексного числа.
Пусть
и
φ = arg z.
Тогда по определению аргумента имеем:
|
|
Отсюда
получается
|
z = a + bi = r(cos φ + i sin |
Такая
форма называется тригонометрической
формой записи комплексного числа.
Как видно, для того, чтобы перейти от
алгебраической формы записи комплексного
числа к тригонометрической форме, нужно
найти его модуль и один из аргументов.
17.
Умножение и деление комплексного числа
в тригонометрической форме?
п.2.
Деление комплексных чисел в
тригонометрической форме записи.
Теорема.
(О делении комплексных чисел в
тригонометрической форме)
Пусть
,
где
и
,
где
–
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
.
(2)
Доказательство.
Воспользуемся следствием формулы Муавра
и правилом умножения комплексных чисел
в тригонометрической форме записи.
Получаем:
,
ч.т.д.
Пример
1. Запишите комплексные числа
и
в
тригонометрической форме и найдите
их произведение
и
частное
.
Решение.
1) Комплексное число
на комплексной плоскостинаходится
во второй четверти, поэтому
,
.
2)
Комплексное число
на комплексной плоскости находится
во четвертой четверти, поэтому
,
.
3)
.
Ответ:
,
.
Пример
2. Вычислить
.
Решение.
Комплексное число
на комплексной плоскостинаходится
в третьей четверти, поэтому
,
Применим
формулу Муавра:
.
Теорема.
(Об умножении комплексных чисел в
тригонометрической форме записи.)
Пусть
,
где
и
,
где
–
два произвольных комплексных числа записанных
в тригонометрической форме. Тогда
.
(13)
Доказательство.
,
ч.т.д.
Теорема
доказана.
Отсюда
вытекает правило умножения комплексных
чисел в тригонометрической форме записи.
Для
того, чтобы перемножить два
комплексных числа в
тригонометрической форме записи нужно
перемножить их модули, а аргументы
сложить.
Следствие
1. Пусть k натуральное число и
.
Пусть далее
,
где
–
произвольные n комплексных чисел
записанных в тригонометрической форме
записи. Тогда
.
Доказательство
проводится индукцией по числу сомножителей
и предоставляется читателю.
Следствие
2. Пусть n натуральное число и
–
произвольное комплексное число в
тригонометрической форме записи. Тогда
.
Доказательство
сразу же следует из Следствия 1.
18. Нахождения корня комплексного числа в тригонометрической форме?
Формула
(6) для произведения двух комплексных
чисел может быть обобщена на случай
сомножителей.
Используя метод математической индукции,
нетрудно показать, что если
-аргументы
чисел
соответственно,
то
Отсюда,
как частный случай, получается формула,
дающая правило возведение комплексного
числа
в целую положительную степень:
(8)
Таким
образом, при
возведении комплексного числа в степень
с натуральным показателем его модуль
возводится в степень с тем же показателем,
а аргумент умножается на показатель
степени.
Формула
(8) называется формулой Муавра.
Число
называется
корнем степени
,
из числа обозначается
,если

Если
=0,
то при любом n
уравнение
имеет
одно и только одно решение z=0.
Пусть
теперь
.Представим
z
и
в тригонометрической форме:
,
.
Тогда
уравнение
примет вид

Два
комплексных числа равны тогда и только
тогда, когда равны их модули, а аргументы
отличаются на число, кратное 2.
Следовательно,
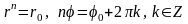
или
.
Таким
образом, все решения уравнения
даются
формулой
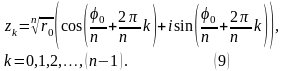
В
самом деле, придавая числу k
в
формуле (9)целые значения, отличные от
0, 1, …, (n-1),
мы не получаем других комплексных
чисел.Формула (9) называется второй
формулой Муавра.Таким
образом, если
,
то существует ровно n
корней степени n
из числа :
все они содержатся в формуле(9).В частности,
если
=2,
то уравнение
имеет два корня:
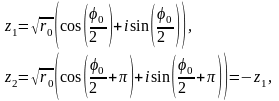
то
есть эти корни симметричны относительно
начала координат.Также из формулы (9)
нетрудно получить, что если
то
точки, изображающие все корни уравнения
,
являются вершинами правильного
n—угольника,
вписанного в
окружность
с центром в точке z=0
и радиусом
.Из
сказанного выше следует, что символ
не
имеет однозначного смысла. Поэтому,
употребляя его, следует четко представлять
себе, что под этим подразумевается.
Например,
используя
запись
,
следует позаботиться о том, чтобы было
ясно, понимается ли под этим пара
комплексных чисел i
и—i,или
одно, и, если одно, то какое именно.
19.
Корни из единицы п-ой степени?


20.
Кольцо многочленов. Операции над
многочленами?
Обозначим
через K(x)
множество многочленов с коэффициентами
из кольца K.
На множестве этих многочленов можно
определить операции сложения и умножения
многочленов. Кольцо многочленов
коммутативно если исходное кольцо
коммутативно.
Операции над многочленами.
Два
полинома считаются равными,
если они составлены в канонической
записи из одинаковых одночленов, т.е.
в том и только в том случае, если
.Суммой
двух полиномов называется полином,
получающийся посредством объединения
одночленов, составляющих слагаемые.
Разумеется, после объединения следует
привести подобные члены. Таким образом,
,
где
.
(Если многочлены f(x)
и g(x)
имеют разное число одночленов, то,
подписав необходимое число одночленов
с нулевыми коэффициентами к одному из
них, в котором число одночленов меньше,
можно добиться их равенства в обоих
многочленах). Поэтому складывать можно
многочлены с разным числом одночленов.
Например,
,
,
преобразуем g(x)
к виду
добавив два нулевых одночлена, суммой
f(x)
и g(x)
будет многочлен
)
Из соотношения
(1)
легко
видеть, что операция суммирования
(сложения) многочленов обладает такими
же свойствами, что и операция сложения
элементов кольца K,
т.е. ассоциативна, коммутативна; полином,
все коэффициенты которого нули, является
нейтральным элементом сложения полиномов;
для каждого полинома существует ему
противоположный, противоположный к
полиному
является полином
.
Итак, множество полиномов с операцией
сложения образует коммутативную группу.
Произведением
двух полиномов называется полином,
составленный из произведений всех
членов первого сомножителя на все члены
второго. Здесь снова возможно приведение
подобных членов. Таким образом,
.
Коэффициент
при
равен
,
если условиться считать, что
при
и
при
.
Принцип вычисления коэффициента
прост: приводятся такие подобные
слагаемые при произведении одночленов
и
,
которые дают в результате одночлены
вида
,
т.е.
—
сумма всевозможных произведений
и
при
.
Поэтому верно равенство
.
(2)
Умножение
многочленов ассоциативно.
Это доказывается следующим образом:
если помимо многочленов
и
дан еще многочлен
,
,
то коэффициентом при
,
в произведении
будет служить элемент
,
а в произведении
— равное ему число
.
Умножение
многочленов дистрибутивно
относительно сложения, это вытекает из
равенства
,
так как левая часть этого равенства
является коэффициентом при
в многочлене
,
а правая часть — коэффициентом при той
же степени переменной
в многочлене
.
Нетрудно
видеть, что многочлен
(где 1 — единица кольца K)
играет роль единицы при умножении
многочленов. Таким образом, множество
полиномов от буквы x
с коэффициентами из кольца составляет
кольцо по отношению к выше определенным
операциям сложения и умножения полиномов
(относительно сложения — это коммутативная
группа; умножение ассоциативно и
дистрибутивно относительно сложения;
существует единичный многочлен). Кольцо
это коммутативно и ассоциативно. Оно
называется кольцом
полиномов
от буквы x
над кольцом K
и обозначается K[x].
В
данном выше определении одночлена и
полинома имеется одно сомнительное
место. Именно, было сказано, что x
есть буква, посторонняя для кольца K,
и не было объяснено, что это значит.
Сказать, что x
не принадлежит кольцу K
— это сказать слишком мало, так как при
этом не исключаются нежелательные
возможности
или
и т.д. Однако мы можем избавиться от
«сомнительной» буквы x.
Для этого рассмотрим бесконечные
последовательности
элементов кольца K,
в которых все элементы, начиная с
некоторого, равны нулю. Вводим теперь
определения равенства и основных
действий.
-
тогда
и только тогда, когда
,
i
= 0, 1, …, k,
… -
.
Ясно, что требование об обращении в
нуль всех членов, начиная с некоторого,
сохраняется при сложении. -
.
Здесь тоже сохраняется требование об
обращении в нуль всех членов, начиная
с некоторого места.
Легко
проверяется коммутативность и
ассоциативность сложения и умножения
и дистрибутивность умножения со
сложением. Далее ясно, что
и
,
и, более общо,
.
4.
отождествляется с последовательностью
.
Рассмотрим
теперь последовательность (0, 1, 0, …, 0,
…), обозначив ее буквой x.
Тогда x2
= (0, 0, 1, 0, …, 0, …) и т.д. Поэтому
.
Таким образом, мы построили элементы
кольца K[x]
полиномов.
Итак,
при определении многочлена
(3)
существенны
лишь коэффициенты
,
и поэтому можно было бы писать вместо
(1) последовательность
.
Однако, в конечном счете, запись многочлена
в виде выражения (3) оказывается более
удобной.
Пусть
,
причем
.
Одночлен
называется высшим
(старшим)
членом
полинома f(x)
и показатель n
называется степенью
f(x)
и обозначается deg
f.
Нулевой полином не имеет высшего члена
в смысле данного определения и считается,
что он равен нулю. Коэффициент
называется свободным
членом.
Многочлен, старший коэффициент которого
равен единице, называется нормированным.При
сложениимногочленов
и
по формуле (1) мы видим, что формула для
суммы не содержит членов, степень которых
выше, чем
,
а формула для произведения — членов,
степень которых выше, чем n
+ m.
21. Деление с остатком в кольце многочленов?
Теорема
1.13.8 (алгоритм деления с остатком в кольце
многочленов). Для любых многочленов
,
,
существуют (и притом единственные)
многочлены
такие, что:
1)f(x)=g(x)q(x)+r(x)
;
2)либо
r(x)=0, либо
,
.
Доказательство-алгоритм
(деление многочленов столбиком).
Пусть
f(x) = anxn+…+a1x+a0, g(x) = bsxs+…+b1x+b0,
.
Если
n<s, то утверждение 1) очевидно:
Пусть
.
Тогда:

Складывая
все эти равенства и сокращая, получаем
т.
е. f(x)=q(x)g(x)+r(x),
где

Если
f(x)=g(x)q(x)+r(x)=g(x)q'(x)+r'(x),
при этом r(x),r'(x)
или равны нулю, или имеют степень, меньшую
чем
,
то g(x)(q(x)-q'(x))=r'(x)-r(x).
Если
,
то получаем противоречие, поскольку
степень левой части
,
а многочлен в правой части или нулевой,
или его степень
.
Итак, q(x)=q'(x),
и поэтому r'(x)=r(x).
Замечание
1.13.9. Если K
— подполе поля K’
(например,
),
,
f(x)=g(x)q(x)+r(x)
— деление с остатком в кольце многочленов
K'[x],
то
.
22. Алгоритм Евклида в кольце многочленов?
Алгори́тм
Евкли́да — алгоритм для нахождения
наибольшего общего делителя двух целых
чисел.Кольца, в которых применим алгоритм
Евклида, называются евклидовыми кольцами.
К ним относятся, в частности, кольца
многочленов.Обобщённый алгоритм Евклида
для многочленов.Алгоритм Евклида и
расширенный алгоритм Евклида естественным
образом обобщается на кольцо многочленов
k[x]
от одной переменной над произвольным
полем k,
поскольку для таких многочленов
определена операция деления с остатком.
При выполнении алгоритма Евклида для
многочленов аналогично алгоритму
Евклида для целых чисел, получается
последовательность полиномиальных
остатков (PRS).
Пример
для кольца Z[x].Пусть
cont(f)
по определению — НОД коэффициентов
многочлена f(x)
из Z[x]
— содержание многочлена. Частное от
деления f(x)
на cont(f)
называется примитивной частью многочлена
f(x)
и обозначается primpart(f(x)).эти
определения понадобятся для нахождения
НОД двух многочленов p1(x)
и p2(x)
в кольце Z[x].
Для многочленов над целыми числами
верно следующее:
НОД
НОД
,
НОД
НОД
.
Таким
образом задача отыскания НОД двух
произвольных многочленов сводится к
задаче отыскания НОД примитивных
полиномов.Пусть есть два примитивных
многочлена p1(x)
и p2(x)
из Z[x],
для которых выполняется соотношение
между их степенями: deg(p1(x))
= m
и deg(p2(x))
= n,
m
> n.
Деление многочленов с остатком
предполагает точную делимость старшего
коэффициента делимого на старший
коэффициент делителя, в общем случае
деление с остатком выполнить невозможно.
Поэтому вводят алгоритм псевдоделения,
который всё же позволяет получить
псевдочастное
и псевдоостаток (prem),
которые будут сами по себе принадлежать
множеству многочленов над целыми
числами.
23. Нод и нок двух многочленов?
Наибольший
общий делитель двух многочленов
Наибольший общий делитель многочленов
f(x)
и g(x)
— такой их общий делитель d(x),
который делится на любой другой их общий
делитель.Алгоритм Евклида (алгоритм
последовательного деления) нахождения
наибольшего общего делителя многочленов
f(x)
и g(x)

Тогда
— наибольший общий делитель f(x)
и g(x).Пусть
cont(f)
по определению — НОД коэффициентов
многочлена f(x)
из Z[x]
— содержание многочлена. Частное от
деления f(x)
на cont(f)
называется примитивной частью многочлена
f(x)
и обозначается primpart(f(x)).эти
определения понадобятся для нахождения
НОД двух многочленов p1(x)
и p2(x)
в кольце Z[x].
Для многочленов над целыми числами
верно следующее:
НОД
НОД
,
НОД
НОД
.
Таким
образом задача отыскания НОД двух
произвольных многочленов сводится к
задаче отыскания НОД примитивных
полиномов.Пусть есть два примитивных
многочлена p1(x)
и p2(x)
из Z[x],
для которых выполняется соотношение
между их степенями: deg(p1(x))
= m
и deg(p2(x))
= n,
m
> n.
Деление многочленов с остатком
предполагает точную делимость старшего
коэффициента делимого на старший
коэффициент делителя, в общем случае
деление с остатком выполнить невозможно.
Поэтому вводят алгоритм псевдоделения,
который всё же позволяет получить
псевдочастное и псевдоостаток (prem),
которые будут сами по себе принадлежать
множеству многочленов над целыми
числами.Под псевдоделением будем
понимать, что самому делению предшествует
умножение полинома p1(x) на ,
то есть
,
,
где
и
—
соответственно псевдочастное и
псевдоостаток.
Итак,
— (принадлежат кольцу многочленов над
целыми числами), причём
.
Тогда алгоритм Евклида состоит из
следующих шагов:
1.
Вычисление НОД содержаний:
-
НОД
.
2.
Вычисление примитивных частей:
.
3.
Построение последовательности
полиномиальных остатков:
4.
Выход и возврат результата:
Если
,
то вернуть c,
иначе вернуть
.
Наименьшее
общее кратное (НОК) двух целых чисел m
и n
— это наименьшее натуральное число,
которое делится на m
и n.
Обозначается НОК(m,n)
или , а в английской литературе lcm(m,n).
24. Корни многочленов. Простые и кратные формы?
Рассмотрим
в комплексной области многочлен, то
есть функцию вида , (8.1)
где
— комплексные числа. Числа называются
коэффициентами многочлена, а натуральное
число n — его степенью.
Определение
8.1. Два многочлена Pn (z) и равны тогда и
только тогда, когда m=n, a0 = b0 , a1 = b1 ,…, an =
bn .
Определение
8.2. Число z0 называется корнем многочлена
(8.1), если Pn (z0) = 0.
Теорема
8.1 (теорема Безу). Остаток от деления
многочлена Pn(z) на z — z0 ( z0 — не обязательно
корень многочлена) равен P(z0).
Доказательство.
Разделив P(z) на z — z0 , получим: P(z) = Q(z)(z —
z0) + r, где число r — остаток от деления,
а Q(z) — многочлен степени, меньшей n. При
подстановке в это равенство z = z0 найдем,
что r = P(z0), что и требовалось доказать.
Теорема
8.2 (основная теорема алгебры). Всякий
многочлен в комплексной области имеет
корень (без доказательства).
Разложение
многочлена в комплексной области на
линейные множители.
Пусть
Pn
(z)
— многочлен степени n,
а z1
— его корень. Тогда по теореме Безу Pn
(z)
можно представить в виде:
Pn
(z)
= (z
— z1)
Qn-1
(z),
где
Qn-1
— многочлен степени n
— 1. Если при этом Qn-1
(z1)
= 0, его вновь можно представить как ( z
— z1
)Qn-2
(z),
a
Pn
(z)
= (z
— z1)Qn-2
(z).
Определение
8.3. Натуральное число k1
называется кратностью корня z1
многочлена Pn
(z),
если этот многочлен делится на , но не
делится на . Корень кратности 1 называется
простым, а корень кратности, большей 1,
— кратным.
Итак,
если z1
— корень Pn
кратности k1
, то Из основной теоремы алгебры следует,
что многочлен тоже имеет корень.
Обозначим его z2
, а его кратность k2
. Тогда а , (8.2)
где
Следовательно, в комплексной области
всякий многочлен можно разложить на
линейные множители.Корень многочлена
(не равного тождественно нулю)
над
полем k
— элемент
,
такой что выполняются два следующих
равносильных условия:данный многочлен
делится на многочлен
;подстановка
элемента c
вместо x
обращает уравнение
в тождество.
Равносильность
двух формулировок следует из теоремы
Безу. В различных источниках любая одна
из двух формулировок выбирается в
качестве определения, а другая выводится
в качестве теоремы.
Свойства
Число
корней многочлена степени n
не превышает n
даже в том случае, если кратные корни
учитывать кратное количество раз.Всякий
многочлен
с комплексными коэффициентами имеет
по крайней мере один, вообще говоря,
комплексный, корень (основная теорема
алгебры) . Аналогичное утверждение верно
для любого алгебраически замкнутого
поля (по определению).Более того, многочлен
с вещественными коэффициентами
можно записать в виде
где
— (в общем случае комплексные) корни
многочлена
,
возможно с повторениями, при этом если
среди корней
многочлена
встречаются равные, то общее их значение
называется кратным корнем.Число
комплексных корней многочлена с
комплексными коэффициентами степени
n,
учитывая кратные корни кратное количество
раз, равно n.
При этом все чисто комплексные корни
(если они есть) многочлена с вещественными
коэффициентами можно разбить на пары
сопряжённых одинаковой кратности, таким
образом, многочлен четной степени с
вещественными коэффициентами может
иметь только чётное число вещественных
корней, а нечётной — только нечётное.Корни
многочлена связаны с его коэффициентами
формулами Виета.
25. Деление многочленов на двух член! Схема Хорнера?
Линейный
двучлен есть многочлен первой степени:
a
x
+ b.
Если разделить многочлен, содержащий
букву x
, на линейный двучлен x
– b,
где b
– некоторое число (положительное или
отрицательное), то остаток будет только
многочленом нулевой степени, т.е.
некоторым числом N
, которое можно определить, не находя
частного. Более точно, это число равно
значению многочлена, получаемому при
x
= b.
Это свойство вытекает из теоремы Безу:
многочлен a0
xm
+ a1
xm-1
+ a2
xm-2
+ …+ am
делится на двучлен x
– b
с остатком N
= a0
bm
+ a1
bm-1
+ a2
bm-2
+ …+ am
.
Д
о к а з а т е л ь с т в о . В соответствии
с определением операции деления
многочленов имеем:
a0
xm + a1 xm-1 + a2 xm-2 + …+ am = ( x – b ) Q + N ,
где
Q
– некоторый многочлен, N
– некоторое число.
Подставим
x
= b
, тогда слагаемое ( x
– b
) Q
обращается в нуль, и мы получаем:
a0
bm + a1 bm-1 + a2 bm-2 + …+ am = N .
З
а м е ч а н и е . При N
= 0 число b
является корнем уравнения:
a0
xm + a1 xm-1 + a2 xm-2 + …+ am = 0 .
Схе́ма
Го́рнера
(или правило Горнера, метод Горнера) —
алгоритм вычисления значения многочлена,
записанного в виде суммы мономов
(одночленов), при заданном значении
переменной. Метод Горнера позволяет
найти корни многочлена, а также вычислить
производные полинома в заданной точке.
Схема Горнера также является простым
алгоритмом для деления многочлена на
бином вида
.
Схема
Горнера
Если
то при делении f(x)
на g(x)
частное q(x)
имеет вид
где
Остаток r находится по формуле

26 Неприводимый многочлен и их свойства
Неприводимый
многочлен
— многочлен,
неразложимый на нетривиальные
(неконстантные) многочлены. Неприводимые
многочлены являются неприводимыми
элементами
кольца
многочленов.
Определение
Неприводимый
многочлен над полем
―
многочлен
от
переменных
над полем
является
простым элементом кольца
,
то есть, непредставим в виде произведения
,
где
и
―
многочлены с коэффициентами из
,
отличные от констант.
Многочлен
называется абсолютно
неприводимым,
если он неприводим над алгебраическим
замыканием поля коэффициентов. Абсолютно
неприводимые многочлены одной переменной
― это многочлены 1-й степени и только
они. В случае нескольких переменных
существуют абсолютно неприводимые
многочлены сколь угодно высокой степени
— например, любой многочлен вида
абсолютно
неприводим.
Свойства
-
Кольцо
многочленовфакториально:
любой многочлен разлагается в произведение
неприводимых многочленов, причем это
разложение определено однозначно с
точностью до постоянных множителей. -
Над
полем вещественных
чисел
любой неприводимый многочлен одной
переменной имеет степень 1 или 2, причем
многочлен 2-й степени неприводим тогда
и только тогда, когда он имеет отрицательный
дискриминант. -
Над
любым полем алгебраических чисел
существуют неприводимый многочлен
сколь угодно высокой степени; например,
многочлен
,
где
и
―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна. -
Если
—
конечное
поле
изэлементов,
а—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из
. -
Предположим
―
целозамкнутое
кольцо
с полем частных(например
и
)
и
―
многочлен одной переменной со старшим
коэффициентом 1, тогдав
,
причеми
имеют
старший коэффициент 1, то
. -
Редукционный
критерий неприводимости.
Пусть задан гомоморфизм
областей
целостности
.
Если степень многочлена
совпадает
со степенью многочленаи
неприводим
над полем частных области,
то не существует разложения,
где
и
отличны от константы.
27 Основная теорема поля комплексных чисел без доказательства и ее следствия
Определение.
Полем называется непустое множество,
для элементов которого определено два
действия, называемых сложением и
умножением, которые удовлетворяют
следующим аксиомам:
1.
(коммутативность
сложения);
2.
(ассоциативность
сложения);
3.
(существование
нуля);
4.
(существование
противоположного элемента);
5.
(коммутативность
умножения);
6.
(ассоциативность
умножения);
7.
(существование
единицы);
8.
(существование
обратного элемента);
9.
(дистрибутивность);
10.
(в
поле должно существовать хотя бы два
элемента).
Пример.
Поля:
–
поле вещественных чисел,
–
поле рациональных чисел,
Некоторые следствия из аксиом поля
1.
Нуль есть только один.
Действительно,
пусть есть два нуля
и
:
Тогда
и
.
2.
У числа есть только одно противоположное.
Действительно,
пусть их два
и
.
Тогда
3.
.
Действительно,
.
4.
.
Действительно,
.
Аналогично
.
Значит,
.
Кроме того,
.
Тогда
и
.
Определение поля комплексных чисел
Определение.
Полем комплексных чисел называется
множество
,
обладающее следующими свойствами:
1.
—
поле;
2.
(
содержит
).
При этом предполагается, что действия
в
в
применении к элементам из
приводят
к тем же результатам, что и действия в
.
3.
Любое квадратное
уравнение
с вещественными коэффициентами имеет
в поле
корень.
4.
Каждый элемент поля
является
корнем какого-либо квадратного уравнения
с вещественными коэффициентами.
Рассмотрим
уравнение
Оно
не имеет вещественных корней, но, по
аксиоме 3, имеет корень в поле
.
Один из корней этого уравнения зафиксируем
и обозначим
(image)
— мнимая единица.
Пусть
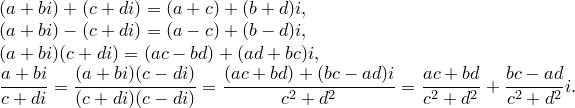
Теорема.
Любой элемент поля
можно
единственным образом представить в
виде
,
где
.
28 Неприводимые многочлены над полем действительных чисел?
Неприводимый
многочлен
— многочлен,
неразложимый на нетривиальные
(неконстантные) многочлены. Неприводимые
многочлены являются неприводимыми
элементами
кольца
многочленов.
Определение
Неприводимый
многочлен над полем
―
многочлен
от
переменных
над полем
является
простым элементом кольца
,
то есть, непредставим в виде произведения
,
где
и
―
многочлены с коэффициентами из
,
отличные от констант.
Многочлен
называется абсолютно
неприводимым,
если он неприводим над алгебраическим
замыканием поля коэффициентов. Абсолютно
неприводимые многочлены одной переменной
― это многочлены 1-й степени и только
они. В случае нескольких переменных
существуют абсолютно неприводимые
многочлены сколь угодно высокой степени
— например, любой многочлен вида
абсолютно
неприводим.
Свойства
-
Над
полем вещественных
чисел
любой неприводимый многочлен одной
переменной имеет степень 1 или 2, причем
многочлен 2-й степени неприводим тогда
и только тогда, когда он имеет отрицательный
дискриминант. -
Над
любым полем алгебраических чисел
существуют неприводимый многочлен
сколь угодно высокой степени; например,
многочлен,
гдеи
―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна. -
Если
—
конечное
поле
изэлементов,
а—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из.
Примеры
Следующие
пять многочленов демонстрируют некоторые
элементарные свойства неприводимых
многочленов:
,
,
,
,
.
Над
кольцом
целых
чисел,
первые два многочлена — приводимые,
последние два — неприводимые. (Третий
вообще не является многочленом над
целыми числами).
Над
полем
рациональных
чисел,
первые три многочлена являются
приводимыми, двое других — неприводимыми.
Над
полем
действительных
чисел,
первые четыре многочлена — приводимые,
но
является
неприводимым. В поле действительных
чисел неприводимыми являются линейные
многочлены и квадратичные многочлены
без действительных корней. Например
разложение многочлена
в
поле действительных чисел имеет вид
.
Оба множителя в данном разложении
являются неприводимыми многочленами.
Над
полем
комплексных
чисел,
все пять многочленов — приводимые.
Фактически, каждый отличный от константы
многочлен
над
может
быть разложен на множители вида:
где
—
степень
многочлена,
—
старший коэффициент,
—
корни
.
Поэтому единственными неприводимыми
многочленами над
являются
линейные многочлены (основная
теорема алгебры).
Конечные поля
Многочлены
с целочисленными коэффициентами, которые
являются неприводимыми над полем
могут
быть приводимыми над конечным
полем.
Например, многочлен
является
неприводимым над
,
но над полем
из
двух элементов мы имеем:
29 Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна?
Неприводимый
многочлен над полем
―
многочлен
от
переменных
над полем
является
простым элементом кольца
,
то есть, непредставим в виде произведения
,
где
и
―
многочлены с коэффициентами из
,
отличные от констант.Многочлен называется
абсолютно
неприводимым,
если он неприводим над алгебраическим
замыканием поля коэффициентов. Абсолютно
неприводимые многочлены одной переменной
― это многочлены 1-й степени и только
они. В случае нескольких переменных
существуют абсолютно неприводимые
многочлены сколь угодно высокой степени
— например, любой многочлен вида
абсолютно
неприводим.
Крите́рий
Э́йзенштейна
— признак неприводимости
многочлена.
Несмотря на (традиционное) название,
является именно признаком, то есть
достаточным условием — но вовсе не
необходимым, Формулировка
Пусть
—
многочлен
над факториальным
кольцом
R
(
),
и для некоторого неприводимого элемента
выполняются
следующие условия:
-
, -
для
любого i от 0 до n-1, -
.
Тогда
многочлен
неприводим
над F
— полем
частных
кольца R.Наиболее
часто этот критерий применяется, когда
R
— кольцо целых чисел
,
а F
— поле рациональных чисел
.Доказательство
Предположим обратное:
,
где
и
многочлены
над F
ненулевых степеней. Из леммы
Гаусса
следует, что их можно рассматривать как
многочлены над R.
Имеем:
По
условию
и
R
факториально, поэтому либо
либо
,
но не то и другое вместе ввиду того, что
.
Пусть
и
.
Все коэффициенты
не
могут делиться на
,
так как иначе бы это было бы верно для
.
Пусть
—
минимальный индекс, для которого
не
делится на
.
Отсюда следует:
Так
как
и
для
всех
то
,
но это невозможно, так как по условию
и
.
Теорема доказана.
30 Векторная пространства. Линейная оболочка векторов?
Линейное,
или векторное
пространство
над
полем
—
это непустое
множество
,
на котором введены операции
-
сложения,
то есть каждой паре элементов множества
ставится
в соответствие элемент того же множества,
обозначаемый
и -
умножения
на скаляр
(то есть элемент поля),
то есть любому элементу
и
любому элементу
ставится
в соответствие единственный элемент
из,
обозначаемый
.
При
этом на операции накладываются следующие
условия:
-
,
для любых(коммутативность
сложения); -
,
для любых
(ассоциативность
сложения); -
существует
такой элемент
,
что
для
любого(существование
нейтрального элемента относительно
сложения),
в частностине
пусто; -
для
любогосуществует
такой элемент
,
что
(существование
противоположного элемента относительно
сложения). -
(ассоциативность
умножения на скаляр); -
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). -
(дистрибутивность
умножения на вектор относительно
сложения скаляров); -
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы
множества
называют
векторами,
а элементы поля
—
скалярами.
Свойства 1-4 совпадают с аксиомами
абелевой группы
Линейная
оболочка
подмножества
линейного
пространства
—
пересечение всех подпространств
,
содержащих
.
Линейная оболочка является подпространством
.
Линейная оболочка также называется
подпространством,
порожденным
.
Говорят также, что линейная оболочка
натянута
на
множество
.
Линейная оболочка
состоит
из всевозможных линейных комбинаций
различных конечных подсистем элементов
из
.
В частности, если
—
конечное множество, то
состоит
из всех линейных комбинаций элементов
.
Если
—
линейно независимое множество, то оно
является базисом
и
тем самым определяет его размерность.
31. Базис и ранг системы векторов?
Определение
1.
Рангом системы векторов называется
максимальное число линейно независимых
векторов системы.
Определение
2.
Базисом системы векторов называется
максимальная линейно независимая
подсистема данной системы векторов.
Теорема.
Если система векторов
линейно-зависима,
то она эквивалентна системе
Доказательстово.
Действительно, пусть
одновременно
неравные нулю числа такие, что
.
Предположим, что
S
0
, разделим эту сумму на
S,
получим:
или
,
где
.
Заменим
систему векторов
эквивалентной
системой
с
помощью следующего элементарного
преобразования:
при
и
.
Тогда вектор
.
Поменяв местами векторы
и
получим
систему вида
.
Что и требовалось доказать.
Следствие.
Произвольную систему векторов
элементарными
преобразованиями можно привести к
системе вида
,
где
линейно
независимая система векторов.
Число
будем
называть рангом системы векторов
,
а систему
–
базисом
системы векторов
.
Отметим,
что ранг системы векторов
не
зависит от конкретной цепочки элементарных
преобразований. Максимально
независимая подсистема системы векторов
называется ее базисом;
векторы, входящие в базис, называются
базисными
векторами.
Будем называть рангом
системы векторов число векторов ее
базиса. Понятно, что если ранг системы
векторов меньше числа k
ее векторов, то она может иметь несколько
базисов.
Понятие базиса распространяется
и на пространство Rn,
которое является системой, содержащей
всю бесконечную совокупность n-мерных
векторов.
Определение
3.
Система n
векторов называется базисом пространства
Rn,если:
1)
векторы этой системы линейно независимы;
2)
всякий вектор из Rn
линейно выражается через векторы данной
системы.
32. Линейная зависимость и линейная независимость систем векторов
Рассмотрим
набор из p
n-мерных
векторов,
обозначим их следующим образом
.
Составим линейную комбинацию этих
векторов и произвольных чисел
(действительных
или комплексных):
.
Отталкиваясь от определения операций
над n-мерными
векторами, а так же свойств операций
сложения векторов и умножения вектора
на число, можно утверждать, что записанная
линейная комбинация представляет собой
некоторый n-мерный
вектор
,
то есть,
.Так
мы подошли к определению линейной
зависимости системы векторов
.Определение.Если
линейная комбинация
может
представлять собой нулевой вектор
тогда, когда среди чисел
есть
хотя бы одно, отличное от нуля, то система
векторов
называется
линейно
зависимой.
Определение.
Если линейная комбинация
представляет
собой нулевой вектор только тогда, когда
все числа
равны
нулю, то система векторов
называется
линейно
независимой.
Свойства
линейной зависимости и независимости.
На основании данных определений,
сформулируем и докажем свойства
линейной зависимости и линейной
независимости системы векторов.
1.Если к линейно зависимой системе
векторов
добавить
несколько векторов, то полученная
система будет линейно зависимой.
Доказательство.Так
как система векторов
линейно
зависима, то равенство
возможно
при наличии хотя бы одного ненулевого
числа из чисел
.
Пусть
.
Добавим к исходной системе векторов
еще s
векторов
,
при этом получим систему
.
Так как
и
,
то линейная комбинация векторов этой
системы вида
представляет
собой нулевой вектор, а
.
Следовательно, полученная система
векторов является линейно зависимой.
1.Если из линейно независимой системы
векторов
исключить
несколько векторов, то полученная
система будет линейно независимой.
Доказательство.
Предположим, что полученная система
линейно зависима. Добавив к этой системе
векторов все отброшенные векторы, мы
получим исходную систему векторов. По
условию – она линейно независима, а в
силу предыдущего свойства линейной
зависимости она должна быть линейно
зависимой. Мы пришли к противоречию,
следовательно, наше предположение
неверно. 1.Если в системе векторов
есть
хотя бы один нулевой вектор, то такая
система линейно зависимая.
Доказательство.Пусть
вектор
в
этой системе векторов является нулевым.
Предположим, что исходная система
векторов линейно независима. Тогда
векторное равенство
возможно
только тогда, когда
.
Однако, если взять любое
,
отличное от нуля, то равенство
все
равно будет справедливо, так как
.
Следовательно, наше предположение
неверно, и исходная система векторов
линейно зависима. 1Если система векторов
линейно
зависима, то хотя бы один из ее векторов
линейно выражается через остальные.
Если система векторов
линейно
независима, то ни один из векторов не
выражается через остальные.
33. Признаки линейной зависимости векторов
Теорема.
При
умножении вектора на число каждая из
его координат умножается на это число,
а при сложении складываются соответствующие
координаты.Доказательство.
Пусть даны два произвольных вектора xи
yи
некоторое произвольное число
.
Разложим векторы по базису l1,
l2,
…, ln,
получим x=x1l1+x2l2+…+xnlnи
y=y1l1+y2l2+…+ynlnи
найдем произведение
и
сумму x
+ y
x+y
= (x1l1+x2l2+…+xnln)+(y1l1+y2l2+…+ynln)=
=(x1+y1)l1+(x2+y2)l2+…+(xn+yn)ln
=>
=>
x+y = [(x1+y1);(x2+y2);…;(xn+yn)].
Доказанная
теорема очень важна в математике, так
как из нее следует признак
линейной зависимости
и независимости
векторов. Покажем это. Пусть в некотором
n
-мерном пространстве Rзадана
система векторов:
|
|
(1) |
Умножим
каждый из векторов на некоторое число
и
сложим их все друг с другом. В результате
получим линейную комбинацию этих же
векторов, которая является новым
вектором, равным, по определению нулю
|
|
(2) |
Распишем
систему (2) в координатной форме
|
|
(3) |
откуда
следует однородная система уравнений
|
|
(4) |
из
коэффициентов которой составляют
матрицу
|
|
(5) |
Равенство
(3) эквивалентно равенствам (2) и (4). На
основании теоремы можно утверждать,
что векторы системы (1) линейно независимы
тогда и только тогда, когда однородная
система (4) имеет единственное нулевое
решение, что на практике обозначает,
что ранг матрицы (5) равен количеству
векторов системы m
34 Необходимые и достаточные условия линейной независимости систем векторов?
.
Система
элементов линейного пространства
{a1,…,an}
называется линейно
независимой,
если
ее линейная комбинация равна нулю только
с нулевыми коэффициентами:

Имеют
место несколько простых утверждений.
Теорема
1 (необходимое
и достаточное условие линейной
независимости).
a1,…,an
– линейно зависима
когда
хотя бы один из элементов является
линейной комбинацией остальных.
{1.(необходимость:
{ak}
– л.з. ):
.
Пусть, для определенности,
а1
– линейная комбинация остальных.
2.(достаточность:
am
– л.к.):
}
Теорема
(необходимое и достаточное условие
линейной независимости в координатной
форме). Cистема
векторов
из
Rn
линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
Следствиями
из этой теоремы являются следующие
утверждения:
-
если
,
то система векторовиз
Rn
— линейно зависима; -
любая
система векторов
из
Rn,
k
> n —
линейно зависима
Теорема
2. Если
один из элементов системы равен нулю,
то вся система линейно зависима.
{
}
Теорема
3.
Если подсистема линейно зависима, то и
вся система линейно зависима.
{
}
35 Линейная зависимость двух векторов на прямой
Определение:
Система векторов
называется
линейно
зависимой,
если хотя бы одна нетривиальная
линейная
комбинация векторов системы обращается
в нуль, т.е. имеет место
равенство
,
при
.
Система
векторов не являющаяся линейно зависимой
называется линейно
независимой.
Определение:
Система векторов
называется
линейно
независимой,
если равенство нулю линейной
комбинации
векторов системы возможно лишь в случае
ее тривиальности, т.е. из
того,
что
следует
.
Теорема:
Если хотя бы один из векторов системы
является нулевым, то эта
система
является линейно зависимой.
Действительно,
из векторов системы
можно
составить линейную комбинацию
,
которая не является тривиальной.
Теорема:
Если часть системы векторов линейно
зависима то и вся система
векторов
линейно зависима.

Действительно,
если система векторов
линейно
зависима, то существует нетривиальная
линейная комбинация
.
Для любой системы векторов
линейная
комбинация
также
является
нетривиальной.
Теорема:
Необходимым и достаточным условием
линейной зависимости двух
векторов
является их коллинеарность.
Действительно,
либо оба коллинеарных вектора равны
нулю, и тогда равна нулю
любая
их линейная комбинация (в том числе и
нетривиальная), либо один из них не
нуль,
и тогда, в силу теоремы из второго
раздела, другой отличается от него на
числовой
множитель. Запишем это:
.
Но эта же запись означает, что
,
и мы имеем нетривиальную линейную
комбинацию, равную нулю.
Наоборот,
допустим, что два неколлинеарных вектора
и
линейно
зависимы. Тогда
существуют
коэффициенты λ и μ такие, что
,
причем, например, λ ≠ 0. Это означает,
что
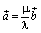
,
и векторы коллинеарны, вопреки нашему
предположению.
Следствие:
Если два вектора неколлинеарны, то они
линейно независимы.
Теорема:
Любой вектор
лежащий
в одной плоскости с неколлинеарными
векторами
и
,
может быть представлен в
виде
линейной комбинации этих векторов (т.е.
найдутся такие вещественные числа
λ
и μ, что
).
Такое
представление
единственно.
Заметим,
прежде всего, что оба вектора
и
отличны
от нуля, так как если
бы
хоть один из них был нулевым, то они были
бы коллинеарны. Если вектор
коллинеарен
одному из данных векторов, то утверждение
сводится к теореме из
второго
раздела.
В
общем случае перенесем все три вектора
в одну точку О
(рис. 6). Через
конец
C
вектора
проведем
прямые CР
и CQ,
параллельные векторам
и
.
Тогда
,
причем векторы
и
коллинеарны
соответственно
и
.
В силу теоремы из второго раздела
существуют и определены однозначно
такие
числа
λ и μ, что
,
.
Таким образом,
,
что и
требовалось.
Допустим
теперь, что существует другая линейная
комбинация
,
равная
,
причем, например
λ
≠ σ. Тогда
,
так
как иначе мы имели бы две прямые,
проходящие через точку C
параллельно
вектору
.
Из
последнего
равенства вытекает, что σ = λ, в противоречие
с нашим
предположением.
36 Линейная зависимость трех векторов на плоскости
|
Утверждение |
|
Доказательство. и , ,
|
|
Утверждение |
|
Доказательство.
согласно 2. Пусть а, , , (рис. и ). = 1 1. 3. Пусть a, b, , , , , , попарно , , ). = 1 1 1.
|
|
Теорема |
|
Теорема |
|
Доказательство. Достаточность.Пусть |
37 Линейная зависимость четырех векторов в пространстве
|
Теорема |
|
Доказательство. d = αa + βb + γc. В силу теоремы 2.2 отсюда |
Если
первые три вектора — некомпланарные,
то четвертый является их линейной
комбинацией
Предложение
Система
векторов
линейно
зависима тогда и только тогда, когда
один из векторов системы является
линейной комбинацией остальных векторов
этой системы.
Доказательство.
Пусть система векторов линейно зависима.
Тогда существует такой набор коэффициентов
,
что
,
причем хотя бы один коэффициент отличен
от нуля. Предположим, что
.
Тогда

то
есть
является
линейной комбинацией остальных векторов
системы.
Пусть
один из векторов системы является
линейной комбинацией остальных векторов.
Предположим, что это вектор
,
то есть
.
Очевидно, что
.
Получили, что линейная комбинация
векторов системы равна нулю, причем
один из коэффициентов отличен от нуля
(равен
).
38 . Базис и размерность над пространством
Определение.
Размерностью
векторного пространства
называется число, равное максимальному
количеству линейно независимых векторов
в этом пространстве.
Определение.Базис
векторного пространства
– это упорядоченная совокупность
линейно независимых векторов этого
пространства, число которых равно
размерности пространства. Приведем
некоторые рассуждения, основываясь на
этих определениях. Рассмотрим пространство
n-мерных
векторов. Покажем, что размерность этого
пространства равна n.
Возьмем систему из n
единичных векторов вида
Примем
эти векторы в качестве строк матрицы
А.
В этом случае матрица А
будет единичной матрицей размерности
n
на n.
Ранг этой матрицы равен n
(при необходимости смотрите статью ранг
матрицы: определение, методы нахождения).
Следовательно, система векторов
линейно
независима, причем к этой системе нельзя
добавить ни одного вектора, не нарушив
ее линейной независимости. Так как число
векторов в системе
равно
n,
то размерность
пространства n-мерных
векторов равна n,
а единичные векторы
являются
базисом этого пространства.
Из последнего утверждения и определения
базиса можно сделать вывод, что любая
система n-мерных
векторов, число векторов в которой
меньше n,
не является базисом.Теперь
переставим местами первый и второй
вектор системы
.
Легко показать, что полученная система
векторов
также
является базисом n-мерного
векторного пространства. Составим
матрицу, приняв ее строками векторы
этой системы. Эта матрица может быть
получена из единичной матрицы перестановкой
местами первой и второй строк,
следовательно, ее ранг будет равен n.
Таким образом, система из n
векторов
линейно
независима и является базисом n-мерного
векторного пространства.Если переставить
местами другие векторы системы
,
то получим еще один базис.Если взять
линейно независимую систему не единичных
векторов, то она также является базисом
n-мерного
векторного пространства.
39 Координаты вектора в данном базисе . Координаты точки
1.
Пусть e1
− базис V1
и а − произвольный вектор из V1.
Отложив эти векторы от
одной точки
О прямой V1
(рис.
2,а)
, так что e1
=
,
а
=
1,
получим, что а
= xe1,
где
(3.1.1)
Введем
на прямой V1
направление: пусть положительное
направление на прямой совпадает с
направлением базисного вектора e1.
Тогда согласно (3.1.1) и (1.1.1) получим
(3.1.2)
Ось,
положительное направление которой
совпадает с направлением вектора e1,
будем называть осью,
определенной
вектором e.
2. Пусть e1,
e2
− базис V2
и а − произвольный вектор из V2.
Отложив эти векторы от одной точки О
плоскости V2
(рис. 2,б),
так что e1
=
1,
e2
=
2,
а
=
,
введя направления на прямых ОЕ1
и OE2,
совпадающие с направлениями базисных
векторов e1
и e2,
получим в соответствии с (3.1.2), что а =
xe1
+ ye2,
(3.1.3)
где
А1,
A2
− проекции точки А на прямые OE1
и OE2
параллельно соответственно прямым OE2
и OE1.
3. Пусть e1,
e2,
e3
− базис V3
и a
− произвольный вектор из V3.
Поступая аналогично (рис.
2,в),
получим а = xe1
+ ye2
+ ze3,
(3.1.4)
где
A1,
A2,
A3
− проекции точки А на прямые OE1,
OE2
и OE3,параллельные
соответственно плоскостям OE2E3,
OE1E3
и OE1E2.
Координатами
точки А в
аффинной системе координат {O; e1,
e2,
e3}
называются координаты радиус — вектора
rA
этой точки в базисе e1,
e2,
e3.
Тот факт, что точка А имеет координаты
x, y, z, обозначают символом А( x, y, z). Итак,
rA
= xe1
+ ye2
+ ze3
⇔
A(x, y, z). 3.2.1
Замечание
1.Из
определения следует, что любая точка А
пространства в заданной системе координат
имеет координаты, причем точки A1(x1,
y1,
z1)
и A2(x2,
y2,
z2)
совпадают тогда и только тогда, когда
x1
= x2,
y1
= y2,
z1
= z2.
40 Скалярное произведение векторов свойства
Скалярным
произведением двух векторов называется
число, равное произведению модулей этих
векторов на косинус угла между
ними.Скалярное произведение векторов
,
обозначается
символом
(порядок
записи сомножителей безразличен, то
есть
).Если
угол между векторами
,
обозначить
через
,
то их скалярное произведение можно
выразить формулой
(1)
Скалярное
произведение векторов
,
можно
выразить также формулой
,
или
.
Из
формулы (1) следует, что
,
если
—
острый угол,
,
если
—
тупой угол;
в
том и только в том случае, когда векторы
и
перпендикулярны
(в частности,
,
если
или
).
Скалярное
произведение
называется
скалярным квадратом вектора и обозначается
символом
.
Из формулы (1) следует, что скалярный
квадрат вектора равен квадрату его
модуля:
.
Если
векторы
и
заданы
своими координатами:
,
,
то
их скалярное произведение может быть
вычислено по формуле
.
Отсюда
следует необходимое и достаточное
условие перпендикулярности двух векторов
.
Угол
между
векторами
,
,
дается
формулой
,
или в координатах
.
Проекция
произвольного вектора
на
какую-нибудь ось uопределяется формулой
,
где
—
единичный вектор, направленный по оси
u. Если даны углы
,
,
,
которые оси uсоставляет с координатными
осями, то
и
для вычисления вектора
может
служить формула
.
2.Свойтсва скалярного произведения векторов.
1.
Скалярное произведение обладает
переместительным свойством: ab=ba

41.
Векторное
произведение векторов. Свойства.
Векторное
произведение —это псевдовектор, перпендикулярный плоскости,
построенной по двум сомножителям,
являющийся результатом бинарной
операции «векторное
умножение» над векторами в
трёхмерном Евклидовом
пространстве.
Произведение не является ни коммутативным,
ни ассоциативным (оно
является антикоммутативным)
и отличается от скалярного
произведения векторов.
Векторное произведение определено
только в трёхмерном и семимерном пространствах.
Результат векторного произведения, как
и скалярного, зависит от метрики Евклидова
пространства.В отличие от формулы для
вычисления по координатам векторов скалярного
произведения в
трёхмерной прямоугольной
системе координат,
формула для векторного произведения
зависит от ориентации прямоугольной
системы координат или, иначе, её
«хиральности».
Иными словами векторным
произведением можно назвать произведение
векторов
и
называется
вектор
,
который определяется следующими
условиями:
1) Его модуль равен
где
—
угол между векторами
и
.
2) Вектор
перпендикулярен
к плоскости, определяемой перемножаемыми
векторами
и
.
3) Вектор
направлен
так, что наблюдателю, смотрящему с его
конца на перемножаемые векторы
и
,
кажется, что для кратчайшего совмещения
первого сомножителя со вторым первый
сомножитель нужно вращать против часовой
стрелки (см. рисунок).
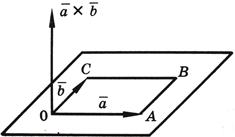
Основные
свойства векторного произведения:
1) Векторное
произведение
равно
нулю, если векторы
и
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2) При перестановке
местами векторов сомножителей векторное
произведение меняет знак на противоположный
С
помощью векторного произведения можно
1)вычислить площадь параллелограмма и
треугольника:
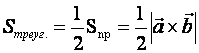
Пример.
Найти площадь параллелограмма,
построенного на векторах
,
,
если
,
.
Решение.
,
Поэтому
.
2)Векторное произведение позволяет
проверить коллинеарность двух векторов:
3)Векторное произведение позволяет
по двум заданным векторам указать
перпендикулярный им вектор
4) Механическая интерпретация векторного
произведения.
42.
Смешанное произведение векторов.
Нахождение объема параллелепипеда с
помощью смешанного произведения.
Смешанным
произведением трех векторов
,
,
называется
число
.
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор
Имеем
∙
,
так как
–
площадь основания построенного на
векторах
,
а
–
высота параллелограмма, то
–
объем параллелограмма построенного на
правой тройке векторов
,
.
Для
левой тройки векторов
Получаем,
, где
–
объем параллелепипеда построенного на
векторах
,
,
.

Свойства
смешанного произведения
1. Смешанное
произведение не меняется при циклической
перестановке его сомножителей (не
меняется ни объем параллелепипеда, ни
ориентация его ребер):
.
2. Смешанное
произведение не меняется
знаков
векторного и скалярного умножения:
, поэтому
смешанное произведение записывают
.
3. Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей:
,
.
4. Смешанное
произведение ненулевых векторов
,
и
равно
нулю тогда и только тогда, когда они
компланарны:
,
,
–
компланарны
.
Доказательство. Предположим,
что векторы
,
и
–
не компланарны. Тогда можно построить
параллелепипед имеющий объем
,
т.е.
,
но это противоречит условию, согласно
которого,
.
Следовательно, векторы
,
и
–
компланарны.
Обратно,
пусть
,
и
–
компланарны. Тогда вектор
и
перпендикулярен плоскости, в которой
находятся векторы
,
и
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
например
Это
значит, что
.
43. Геометрический смысл скалярного, векторного и смешанного произведения.
Пусть
и
—
два ненулевых вектора. Если отложить
их от одной точки
,
получится угол между
этими векторами (точнее между несущими
их полупрямыми, исходящими из точки
).
Этот угол обозначают
.
Скалярным
произведением двух векторов называется
число, равное произведению длин этих
векторов на косинус угла между ними:
Если
один из векторов нулевой, то угол не
определен, и произведение считают равным
нулю.
Геометрический
смысл скалярного произведения
1)Связь
с проекциями
Алгебраическое
значение проекции вектора
на
вектор
вдоль
прямой, перпендикулярной
,
очевидно, равно
Аналогично
Таким
образом, скалярное произведение
2)Связь
с длинами
Рассмотрим
скалярное произведение вектора на
самого себя.
3)Связь
с углами
Рассмотрим
скалярное произведение единичных
векторов. Поскольку их длины равны 1, то
Векторное
произведение —это псевдовектор, перпендикулярный плоскости,
построенной по двум сомножителям,
являющийся результатом бинарной
операции «векторное
умножение» над векторами в
трёхмерном Евклидовом
пространстве.
Произведение не является ни коммутативным,
ни ассоциативным (оно
является антикоммутативным)
и отличается от скалярного
произведения векторов.
Геометрические свойства векторного произведения
Модуль
векторного произведения
равняется
площади
параллелограмма,
построенного на приведённых к общему
началу векторах
и
(Если
— единичный
вектор,
ортогональный векторам
и
и
выбранный так, что тройка
—
правая, а
—
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
При использовании векторного и скалярного
произведений можно высчитать объём
параллелепипеда, построенного на
приведённых к общему началу
векторах a, b и c.
Такое
произведение трех векторов
называется смешанным.
Величина
векторного произведения зависит
от синуса угла
между изначальными векторами, поэтому
векторное произведение может восприниматься
как степень «перпендикулярности»
векторов также, как и скалярное
произведение может
рассматриваться как степень
«параллельности». Векторное произведение
двух единичных
векторов равно
1 (единичному вектору), если изначальные
векторы перпендикулярны, и равно 0
(нулевому вектору), если векторы
параллельны либо антипараллельны.
Смешанным
произведением трех векторов
,
,
называется
число
.
Геометрический
смысл смешанного произведения: модуль
смешанного произведения трех векторов
численно равен объему параллелепипеда,
построенного на этих векторах.Пусть
ребрами параллелограмма являются
векторы
,
,
образующие
правую тройку векторов и вектор
Имеем
∙
,
так как
–
площадь основания построенного на
векторах
,
а
–
высота параллелограмма, то
–
объем параллелограмма построенного на
правой тройке векторов
,
.
Для
левой тройки векторов
.
Получаем,
, где
–
объем параллелепипеда построенного на
векторах
,
,
.
44.Аффинная система координат. Прямоугольная система координат?
Пусть
в пространстве V3
(на плоскости V2
или на прямой V1)
зафиксиоована некотороая точка О,
называемая полюсом.
Для любой точки А вектор rA
=
называется
радиус
— вектором точки А относительно полюса
О.
Задание точки ее радиус — вектором
определяет, очевидно, биективное
отображение. Тот факт, что точка А имеет
радиус — вектор r, обозначают символом
А(r).
Если в пространстве V3
завиксираваны точка О и базис e1,
e2,
e3,
то говорят, что в пространстве задана
аффинная
система координат
(или общая
декартова система координат)
{O; e1,
e2,
e3}.
Точка О называется началом
координат;
оси, проходящие через начало координат
и определенные векторами e1,
e2,
e3,
называются осями
коордиеат
и обозначаются Ох (ось абцисс), Оу (ось
ординат), Oz (ось аппликат) соответственно.
Плоскость, определяемая осями координат
Ох и Оу (Ox и Oz, Oy и Oz), называется координатной
плоскостью Oxy (Oxz,
Oyz соответственно). В этой терминалогии
аффинная система координат обозначается
также символом Oxyz.
Координатами
точки А в
аффинной системе координат {O; e1,
e2,
e3}
называются координаты радиус — вектора
rA
этой точки в базисе e1,
e2,
e3.
Тот факт, что точка А имеет координаты
x, y, z, обозначают символом А( x, y, z). Итак,
rA
= xe1
+ ye2
+ ze3
⇔
A(x, y, z). 3.2.1
Замечание
1.Из
определения следует, что любая точка А
пространства в заданной системе координат
имеет координаты, причем точки A1(x1,
y1,
z1)
и A2(x2,
y2,
z2)
совпадают тогда и только тогда, когда
x1
= x2,
y1
= y2,
z1
= z2.
Замечание
2.Координаты
точки A(x, y, z) определяются соотношениями
(3.1.4)
. При этом, как легко видеть, проекции
A1,
A2,
A3
точки А имеют координаты A1(x,
0, 0), A2(0,
y, 0), A3(0,
0, z) .
Аналогично определяются аффинные
системы координат {O; e1,
e2}
на плоскости V2
и {O; e1}
на прямой V1,
а также координаты точки А(x, y) и A(x)
соответственно. При этом имеют место
очевидные аналоги соотношения (3.2.1) и
обоих замечаний. В дальнейшем все факты
будем излагать только в терминах V3.
Теорема 3.1Если
A(x1,
y1,
z1)
и B(x2,
y2,
z2)
− точки пространства, заданные своими
координатами в системе координат {O; e1,
e2,
e3},
то вектор а =
в
базисе e1,
e2,
e3имеет
координаты а = {x2
= x1,
y2
= y1,
z2
= z1}.
Д
оказательство.
Действительно,
=
−
(рис.
1) и, следовательно, а = rB
− rA.
Так как rA
= {(x1,
y1,
z1},
rВ
= {(x2,
y2,
z2},
то в силу свойства линейности координат
отсюда следует утверждение теоремы.
Теорема
доказана.
Деление отрезка в данном
отношении. Гворят, что точка М ≠ В делит
отрезок [АВ] в отношении λ, если
=
λ
(рис.
2).
Обозначение:
(АВМ) = λ. Из определения следует, что
точка М расположена на прямой АВ, при
этом (рис. 2):
-
если
М − внутренняя точка отрезка [AB], то λ
> 0; -
если
М = А, то λ = 0; -
если
М расположена вне отрезка [AB], то λ <
0.
Заметим,
что других вариантов расположения точки
М не может быть и что в одном из возможных
вариантов λ не равно -1.
Теорема
3.2Пусть
A(r1),
B(r2),
M(r3)
− точки пространства и (АВМ) = λ. Тогда
(3.2.2)
Доказательство.
Условие (АВМ) = λ означает, что
=
λ
или r3−
r1
= λ(r2
−r3).
Отсюда следует (3.2.2). Теорема
доказана.
Следствие.Соотношение
(3.2.2) в координатной форме имеет следующий
вид: для A(x1,
y1,
z1),
B(x2,
y2,
z2),
М(x3,
y3,
z3)
(3.2.3)
Прямоугольные
координаты. Базис e1,
… ,en,
где n = 1, 2, 3, называется ортонормированным,
если векторы базиса
-
имеют
единичную длину и, в случае n >1, -
попарно
перпендикулярны. -
Аффинная
система координат {O; e1,
e2,
e3},
соответствующая ортонормированному
базису e1,
e2,
e3,
называется прямоугольной
декартовой системой координат.
45 Радиус Вектора Расстояние между двумя точками
|
Расстояние |
Проведем
через точки
и
прямые,
параллельные оси z.
Пусть эти прямые пересекут плоскость xy в
точках
и
Заметим,
что поскольку эти точки лежат в
плоскости xy,
то координата z у
них равна нулю. Проведем плоскость через
точку
параллельную
плоскости xy.
Пусть эта плоскость пересекает прямую
в
точке C.
Применим теорему Пифагора к
треугольнику
Очевидно,
что отрезки
и
равны,
а согласно теореме Пифагора на плоскостиxy,
получаем, что
Поскольку
длина отрезка
равна
то
окончательно имеем
Если
же окажется, что отрезок
параллелен
оси z,
то
Но
тот же результат дает полученная формула,
так как в этом случае
Итак,
доказана следующая
Теорема 9.7.
Расстояние
между точками A1 и A2 можно
вычислить по формуле
|
|
Определение 9.14.
Вектор,
конец которого совпадает с данной
точкой, называется радиус-вектором данной
точки.
Ра́диус-ве́ктор (обычно
обозначается
или
просто
)
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.
Для
произвольной точки в пространстве,
радиус-вектор — это вектор, идущий из
начала координат в эту точку.
Длина
радиус-вектора,
или его модуль, определяет расстояние,
на котором точка находится от начала
координат, а стрелка указывает направление
на эту точку пространства.
На
плоскости углом радиус-вектора называется
угол, на который радиус-вектор повёрнут
относительно оси
абсцисс в
направлении против часовой стрелки.
46 Уравнение прямой на плоскости
Определение.
Любая
прямая на плоскости может быть задана
уравнением первого порядка
Ах
+ Ву + С = 0,
причем
постоянные А, В не равны нулю одновременно.
Это уравнение первого порядка называют
общим
уравнением прямой. В
зависимости от значений постоянных А,В
и С возможны следующие частные случаи:
• C
= 0, А ≠0, В ≠ 0 – прямая проходит через
начало координат
• А
= 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна
оси Ох
• В
= 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна
оси Оу
• В
= С = 0, А ≠0 – прямая совпадает с осью Оу
• А
= С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение
прямой может быть представлено в
различном виде в зависимости от каких
– либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали
Определение.
В
декартовой прямоугольной системе
координат вектор с компонентами (А, В)
перпендикулярен прямой , заданной
уравнением Ах + Ву + С = 0.
Пример.
Найти уравнение прямой, проходящей
через точку А(1, 2) перпендикулярно вектору
(3,
-1).
Решение.
Составим при А = 3 и В = -1 уравнение прямой:
3х – у + С = 0. Для нахождения коэффициента
С подставим в полученное выражение
координаты заданной точки А. Получаем:
3 – 2 + C = 0, следовательно С = -1. Итого:
искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки
Пусть
в пространстве заданы две точки M 1
( x
1
, y
1
, z
1
) и M2
( x 2,
y 2
, z 2
), тогда уравнение прямой, проходящей
через эти точки:

Если
какой- либо из знаменателей равен нулю,
следует приравнять нулю соответствующий
числитель.На плоскости записанное выше
уравнение прямой упрощается:

если
х
1
≠ х2
и х = х
1
, если х
1
= х2
.
Дробь
=
k называется угловым
коэффициентом прямой.
Уравнение прямой по точке и направляющему вектору
По
аналогии с пунктом, рассматривающим
уравнение прямой через вектор нормали
можно ввести задание прямой через точку
и направляющий вектор прямой.
Определение.
Каждый
ненулевой вектор
(
α1
, α2
), компоненты которого удовлетворяют
условию А α1
+ В α2
= 0 называется направляющим вектором
прямой
Ах
+ Ву + С = 0.
Пример.
Найти уравнение прямой с направляющим
вектором
(1,
-1) и проходящей через точку А(1, 2).
Решение.
Уравнение искомой прямой будем искать
в виде: Ax + By + C = 0. В соответствии с
определением, коэффициенты должны
удовлетворять условиям:
1
* A + (-1) * B = 0, т.е. А = В.
Тогда
уравнение прямой имеет вид: Ax + Ay + C = 0,
или x + y + C / A = 0. при х = 1, у = 2 получаем С/
A = -3, т.е. искомое уравнение:
х
+ у — 3 = 0
47 Нормальный и направляющий вектор на прямой
Всякое
уравнение первой степени относительно
координат x,
y, z
Ax
+ By
+ Cz
+D
= 0 (3.1)
задает
плоскость, и наоборот: всякая плоскость
может быть представлена уравнением
(3.1), которое называется уравнением
плоскости.
Вектор
n
(A, B, C ), ортогональный плоскости, называется
нормальным
вектором
плоскости. В уравнении (3.1) коэффициенты
A, B, C одновременно не равны 0.
Особые
случаи уравнения (3.1):
1.
D = 0, Ax+By+Cz = 0 — плоскость проходит через
начало координат.
2.
C = 0, Ax+By+D = 0 — плоскость параллельна оси
Oz.
3.
C = D = 0, Ax +By = 0 — плоскость проходит через
ось Oz.
4.
B = C = 0, Ax + D = 0 — плоскость параллельна
плоскости Oyz.
Уравнения
координатных плоскостей: x = 0, y = 0, z = 0.
Прямая
в пространстве может быть задана:
1)
как линия пересечения двух плоскостей,т.е.
системой уравнений:
A
1
x
+ B 1
y
+ C 1
z
+ D 1
= 0, A 2
x
+ B 2
y
+ C 2
z
+ D 2
= 0; (3.2)
2)
двумя своими точками M 1
(x 1,
y 1,
z 1
) и M 2
(x 2,
y 2,
z 2
), тогда прямая, через них проходящая,
задается уравнениями:
=
;
(3.3)
3)
точкой M 1
(x 1,
y 1,
z 1
), ей принадлежащей, и вектором a
(m,
n, р), ей коллинеарным. Тогда прямая
определяется уравнениями:
.
(3.4)
Уравнения
(3.4) называются каноническими
уравнениями прямой.
Вектор
aназывается
направляющим
вектором прямой.
Параметрические
уравнения прямой получим,
приравняв каждое из отношений (3.4)
параметру t:
x
= x
1
+
mt
, y
= y
1
+
nt
, z
= z
1
+
р t
. (3.5)
Решая
систему (3.2) как систему линейных уравнений
относительно неизвестных xи
y,
приходим к уравнениям прямой в проекциях
или к приведенным
уравнениям прямой:
x
= mz
+ a,
y
= nz
+ b.
(3.6)
От
уравнений (3.6) можно перейти к каноническим
уравнениям, находя zиз
каждого уравнения и приравнивая
полученные значения:
.
От
общих уравнений (3.2) можно переходить к
каноническим и другим способом, если
найти какую-либо точку этой прямой и ее
направляющий вектор n
=
[ n1,
n2
], где n1
(A 1,
B 1,
C 1
) и n2
(A 2,
B 2,
C 2
) — нормальные векторы заданных плоскостей.
Если один из знаменателей m,
nили
р
в уравнениях (3.4) окажется равным нулю,
то числитель соответствующей дроби
надо положить равным нулю, т.е. система
равносильна
системе
;
такая прямая перпендикулярна к оси Ох.
Система
равносильна
системе x = x 1,
y = y 1
; прямая параллельна оси Oz.
48 Расположение двух прямых Условия параллельности и перпендикулярности прямых
Условие
параллельности.
Если прямые линии параллельны, то они
наклонены к числовой оси ОХ под одним
и тем же углом, следовательно, разница
углов наклона параллельных прямых равна
нулю (действительно они никогда не
пересекаются). Тангенс угла в ноль
градусов (ноль радиан) равен нулю. То
есть левая часть уравнения (1-4) равна
нулю, тогда нулю должна быть равна и
правая часть данного выражения. Дробь
равна нулю если числитель равен нулю.
В нашем случае это может быть при:
k2
= k1.
(1-5)
Это
и есть условие параллельности двух
прямых линий.
Условие
перпендикулярности
Если две прямых линии взаимно
перпендикулярны, то угол между ними
равен 90 или П/2 радиан.
Тангенс такого угла не существует
(иногда говорят, что он равен бесконечности).
Правая часть (1-4) не существует при
равенстве нулю знаменателя, т.е.
k2
* k1 = -1.
(1-6)
|
Условие Условие k1k2=-1 Пример Решение. |
Расположение
двух прямых
Если
прямые заданы уравнениями
и
то
они:
1)
параллельны (но не совпадают)
2)
совпадают
3)
пересекаются
4)
скрещиваются
Если
то
случаи 1 — 4 имеют место, когда (
—
знак отрицания условия):
1)
2)
3)

4)

49.Угол между двумя прямыми
Угол
между двумя прямыми равен углу между
их направляющими векторами. Таким
образом, если вам удастся найти координаты
направляющих векторов a = (x1;
y1;
z1)
и b = (x2;
y2;
z2),
то сможете найти угол. Точнее, косинус
угла по формуле:
Посмотрим,
как эта формула работает на конкретных
примерах:
-
Задача.
В кубе ABCDA1B1C1D1 отмечены
точки E и F — середины
ребер A1B1 и B1C1соответственно.
Найдите угол между прямыми AE и BF.

Решение.
Поскольку ребро куба не указано,
положим AB = 1. Введем стандартную
систему координат: начало в точке A,
оси x, y, z направим вдоль AB,
AD и AA1соответственно.
Единичный отрезок равен AB = 1. Теперь
найдем координаты направляющих векторов
для наших прямых.
Найдем
координаты вектора AE. Для этого нам
потребуются точки A = (0; 0; 0)
и E = (0,5; 0; 1). Поскольку
точка E — середина отрезка A1B1,
ее координаты равны среднему
арифметическому координат концов.
Заметим, что начало вектора AE совпадает
с началом координат, поэтому
AE = (0,5; 0; 1).
Теперь
разберемся с вектором BF. Аналогично,
разбираем точки B = (1; 0; 0)
и F = (1; 0,5; 1), т.к. F —
середина отрезка B1C1.
Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) =
(0; 0,5; 1).
Итак,
направляющие векторы готовы. Косинус
угла между прямыми — это косинус
угла между направляющими векторами,
поэтому имеем:
Ответ:
arccos 0,8
50.Расстояние от точки до прямой
Расстоянием
от точки до прямой называется
длина перпендикуляра, опущенного из
точки на прямую.
Если точка M0∈l ,
то ρ(M0,l)=0 (расстояние
от точки M0 до
прямой l)
Для
всякой точки M2/=M1 M0M2>M0M1
Найдем ρ(M0,l) —
?
Oi→j→− прямоугольная
система координат;
M0(x0,y0);M1(x1,y1);
−−−−−−−→M0M1⊥l и −→n⊥l ;
−−−−−−−→M0M1∣∣−→n ,
тогда
−−−−−−−→M0M1·−→n=∣ ∣ −−−−−−−→M0M11∣ ∣ ·∣−→n∣(±1)
−−−−−−−→M0M1(x1−x0,y1−y0);−→n(A,B);
−−−−−−−→M0M1·−→n=A(x1−x0)+B(y1−y0)=Ax1+By1−(Ax0+By0), т.к. M1(x1,y1)∈l⇒Ax1+By1+C=0 ,
следовательно, последнее выражение
можно переписать в виде:
−−−−−−−→M0M1·−→n=A(x1−x0)+B(y1−y0)=−(С+Ax0+By0)
Длина
вектора −−→∣n∣=√A2+B2
Подставим
все в выражение (1):
−(С+Ax0+By0)=±ρ(M0,l)√A2+B2
Откуда
получим конечное
выражение для нахождения расстояния
от точки до прямой:
ρ(M0,l)=√A2+B2∣ ∣ Ax0+By0+С∣ ∣
Если у вас нет времени на выполнение заданий по матрицам, вы всегда можете попросить меня, пришлите задания мне в 
 Ответы на вопросы по заказу заданий по матрицам:
Ответы на вопросы по заказу заданий по матрицам:

- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

- Доработка бесплатна. Срок выполнения от 1 до 2 дней.

- Оценка стоимости бесплатна.

- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

- Присылайте в любое время! Я стараюсь быть всегда онлайн.

Содержание:
- Ответы на вопросы по заказу заданий по матрицам:
- Матрицы
- Задача 1:
- Задачи с решением
- Задача 2:
- Задача 3:
- Задача 4:
- Задача 5:
- Задача 6:
- Задача 7:
- Задача 8:
- Задача 9:
- Задача 10:
- Задача 11:
- Задача 12:
- Задача 13:
- Задача 14:
- Задача 15:
- Задача 16:
- Задача 17:
- Задача 18:
- Задача 19.
- Задача 20.
- Задача 21.
Матрицы
ОПРЕДЕЛЕНИЕ. Матрицей размера 



Числа называются элементами матрицы. Матрица может быть записана так:
Матрица размера 


ОПРЕДЕЛЕНИЕ. Матрица называется квадратной, если число строк равно числу столбцов 

ОПРЕДЕЛЕНИЕ. Главной диагональю квадратной матрицы называется диагональ, составленная из элементов 

ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие ниже (или выше) главной диагонали, равны нулю, называется треугольной, например:
ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие выше и ниже главной диагонали, равны нулю, называется диагональной, Т.е. 
ОПРЕДЕЛЕНИЕ. Квадратная диагональная матрица с единичными элементами называется единичной и обозначается буквой 
ОПРЕДЕЛЕНИЕ. Транспонированием квадратной матрицы называется такое преобразование, при котором ее строки становятся столбцами с теми же номерами, а столбцы — строками.
Матрицу, транспонированную по отношению к матрице 
Например, 

ОПРЕДЕЛЕНИЕ. Матрица называется нулевой, если все ее элементы равны нулю.
ОПРЕДЕЛЕНИЕ. Матрицы 
Определители второго и третьего порядка ОПРЕДЕЛЕНИЕ. Определителем второго порядка квадратной матрицы

Возможно, вас также заинтересует эта ссылка:
Задача 1:
ОПРЕДЕЛЕНИЕ. Определителем третьего порядка квадратной матрицы

Данная формула называется правилом треугольников. Элементы определителя изображаются кружками, а соответствующие произведения отрезками или треугольниками.
Знаки (+) и (-) соответствуют знакам определенных слагаемых, входящих в определитель (4).
Возможно, вас также заинтересует эта ссылка:
Задачи с решением
Задача 2:
Свойства определителей
Свойство 1. Определитель квадратной матрицы 
Свойство 2. При перестановке местами двух строк (столбцов) определитель 
Свойство 3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
Свойство 4. Общий множитель для элементов некоторой строки (столбца) определителя 
Это свойство можно сформулировать иначе: умножение всех элементов некоторой строки (столбца) определителя 

Свойство 5. Если все элементы некоторой строки (столбца) определителя 
Это свойство вытекает из предыдущего при
Свойство 6. Если все элементы двух строк (столбцов) определителя 
Свойство 7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
Свойство 8. Если к элементам какой-нибудь строки (столбца) определителя 

Замечание: пользуясь свойством 8, можно, не меняя величину определителя, все элементы некоторой строки (столбца) определителя, кроме одного, сделать равными нулю.
ОПРЕДЕЛЕНИЕ. Минором 





Возможно, вас также заинтересует эта ссылка:
Задача 3:
Найдите минор 

- Решение:
ОПРЕДЕЛЕНИЕ. Алгебраическим дополнением 






Возможно, вас также заинтересует эта ссылка:
Задача 4:
Для определителя
Свойство 9. Определитель 
Задача 5:
Вычислим определитель 3-го порядка разложением по элементам первой строки:
Свойство 10. Алгебраическая сумма произведений элементов любой строки (столбца) определителя 
Определители высших порядков
Определитель квадратной матрицы 
Для определителей 
Определители 
1. Метод разложения по строке или столбцу (метод понижения порядка):
Задача 6:
Вычислим определитель 4-го порядка 
- Решение:
Обозначим строки определителя через 


Обратим в нули элементы первого столбца во второй, третьей и четвертой строках с помощью преобразований

Метод приведения к треугольному виду.
Используя свойства, добьемся такой структуры определителя, при которой все его элементы, стоящие ниже главной диагонали, равны нулю. Тогда определитель будет численно равен произведению элементов, стоящих на главной диагонали.
Задача 7:
Вычислим определитель 5-го порядка 
- Решение:
Операции над матрицами и их свойства
ОПРЕДЕЛЕНИЕ: Суммой матриц 



Свойство 1.
Свойство 2.
Свойство З.
ОПРЕДЕЛЕНИЕ: Произведением матрицы 



Свойство 4.
Свойство 5.
Свойство 6.
Свойство 7.
Свойство 8.
Задача 8:
Найдите 
- Решение:
ОПРЕДЕЛЕНИЕ: Произведением матрицы 





т.е. 




Задача 9:
Найдите 
- Решение:
размерность матрицы
Свойство 9.
Свойство 10.
Свойство
ОПРЕДЕЛЕНИЕ: Матрицы 

Задача 10:
Найдите 
- Решение:
Свойство 12.
Свойство 13.
Свойство 14.
Свойство 15.
ОПРЕДЕЛЕНИЕ: Квадратная матрица 

ОПРЕДЕЛЕНИЕ: Матрица 

Основным методом вычисления обратной матрицы 
ОПРЕДЕЛЕНИЕ: Матрица 



Теорема. Если матрица 



Свойство 16.
Свойство 17
Свойство 18.
.
Матричные уравнения
ОПРЕДЕЛЕНИЕ: Если матрицы 

Если 


т.к. 
Задача 11:
решите матрическое уравнение
- Решение:
Вычислим 

Построим матрицу 
Записываем решение матричного уравнения:
Ранг матрицы
Пусть в матрице 





ОПРЕДЕЛЕНИЕ. Определитель 

ОПРЕДЕЛЕНИЕ. Рангом матрицы 


ОПРЕДЕЛЕНИЕ. Базисным минором матрицы 

ОПРЕДЕЛЕНИЕ. Матрицы называются эквивалентными и обозначаются 
Ранг матрицы 
1. Метод окаймляющих миноров
Пусть в матрице 




Если 

Выбираем отличный от нуля минор 2-го порядка 


2. Метод элементарных преобразований
К элементарным преобразованиям матрицы относятся:
1)транспонирование;
2) перестановка строк (столбцов);
3) умножение строки (столбца) на число
4) прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число;
5) отбрасывание нулевой строки (столбца) матрицы.
Теорема. Элементарные преобразования матрицы не меняют ее ранга.
Определение ранга матрицы 


Задача 12:
Вычислите ранг матрицы 
- Решение:
Системы 

Рассмотрим систему линейных уравнений вида
ОПРЕДЕЛЕНИЕ: Решением системы линейных уравнений (1) называется такое множество чисел 
Система (1) может быть записана в матричном виде 




ОПРЕДЕЛЕНИЕ: Система линейных уравнений называется совместной, если она имеет решения, и называется несовместной — в противном случае. Система называется определенной, если она имеет единственное решение, и называется неопределенной, если она имеет бесконечное множество решений.
Системы 

Рассмотрим систему вида

Теорема (правило Крамера). Если главный определитель системы линейных уравнений (1) не равен нулю, то система совместна и определена, причем единственное решение вычисляется по формулам Крамера:
Здесь 


Доказательство:

a 

Чтобы найти неизвестное 



В этом уравнении выражение
где 
поскольку представляют собой сумму произведений элементов 

В правой части уравнения имеем
Таким образом, уравнение примет вид 



Задача 13:
Решите систему:
По формулам Крамера:
Посчитаем значения неизвестных:
Системы 

Рассмотрим систему линейных уравнений вида
Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений (3) была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы:
Если 
Задача 14:
Решите систему
по теореме Кронекера — Капелли система несовместна. Если 
1) 
2) 
Схема отыскания решения системы 

Пусть 
минор, составленный из коэффициентов матрицы порядка 





Тогда 

Перенесем свободные неизвестные в правую часть уравнений системы:
Система (4) является следствием исходной системы (3) и ее решение может быть найдено или по формулам Крамера, или матричным способом. При этом базисные неизвестные 
то базисные неизвестные выражаются через свободные
Общее решение неоднородной системы 
Поскольку свободные неизвестные могут принимать произвольные числовые значения, то исходная система имеет бесконечно много решений. Общее решение 



Задача 15:
Решите систему
Рассмотрим расширенную матрицу системы:
Следовательно, 

Полагая 

Однородные системы
Однородная система имеет вид:
ей соответствует матричное уравнение
Однородная система всегда совместна, так как 
Теорема. Для того чтобы однородная система имела ненулевое решение, необходимо и достаточно, чтобы
Следствие. Для того чтобы однородная система
линейных уравнений с
неизвестными имела ненулевое решение, необходимо и достаточно, чтобы
Если 


Общее решение 

и совпадает с соответствующим общим решением неоднородной системы при
Задача 16:
Решите систему
Рассмотрим матрицу системы:
Следовательно, 

Полагая 


Метод Гаусса решения систем 

Одним из основных методов решения систем линейных уравнений является метод Гаусса.
Эквивалентными преобразованиями системы являются следующие:
Элементарным преобразованиям уравнений соответствуют элементарные преобразования элементов расширенной матрицы системы 
Сформулируем алгоритм Гаусса как преобразование строк матрицы 

Наиболее удобен метод Гаусса — Ньютона, в котором матрицу приводят не к треугольному, а к диагональному виду. При этом сразу получается решение системы уравнений.
Задача 17:
Решите систему
Запишем расширенную матрицу системы
Ранг основной матрицы системы равен трем, совпадает с рангом расширенной матрицы системы, следовательно, по теореме Кронекера — Капелли система линейных уравнений совместна. Вернемся к системе уравнений:
Решение задач:
Задача 18:
Вычислите ранг матрицы
- Решение:
В левом верхнем углу матрицы стоит определитель треугольного вида, который равен произведению элементов, стоящих на его главной диагонали 
Ответ: ранг матрицы равен 4.
Задача 19.
Решите систему линейных уравнений
- Решение:
Запишем расширенную матрицу системы
Если 
Вычислим основной определитель матрицы системы 
Чтобы получить определитель 

Аналогично вычисляем
Отсюда
Ответ:
Задача 20.
Решите систему линейных уравнений
- Решение:
Запишем расширенную матрицу системы
Ранг основной матрицы системы равен единице и совпадает с рангом расширенной матрицы системы, следовательно, по теореме Кронекера — Капелли система линейных уравнений совместна. Она равносильна уравнению:
В качестве базисного неизвестного выберем 

Итак,
Ответ: 
Задача 21.
Решите систему линейных уравнений
- Решение:
Запишем расширенную матрицу системы
В левом верхнем углу матрицы стоит треугольный определитель 
углу матрицы стоит треугольный определитель
матрицы системы линейных уравнений равен трем и равен рангу ее расширенной матрицы, следовательно, система совместна по теореме Кронекера — Капелли. Для удобства продолжим преобразования матрицы и приведем базисный минор не только к треугольному, но и к диагональному виду. С помощью преобразований получим:
Восстановим по полученной матрице решение системы уравнений:
Базисный минор содержит базисные неизвестные 


Ответ:
Возможно, вас также заинтересует эта ссылка:


 нужно сделать sum+=s; Получится sum = 3; Потом s обнулилось и пошла считаться вторая строка. Например стало s = 2. И если sum+=s; Вы поставили верно, то в конце у вас выведется верная сумма двух сумм строк
нужно сделать sum+=s; Получится sum = 3; Потом s обнулилось и пошла считаться вторая строка. Например стало s = 2. И если sum+=s; Вы поставили верно, то в конце у вас выведется верная сумма двух сумм строк Сообщение было отмечено nonameprogger как решение
Сообщение было отмечено nonameprogger как решение







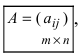
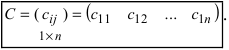
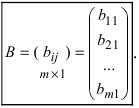
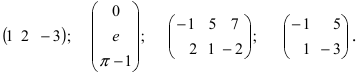


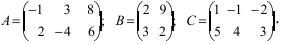
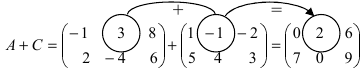
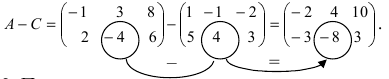

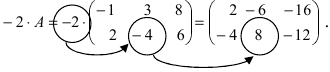
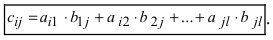
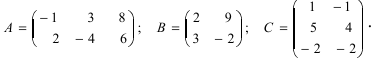
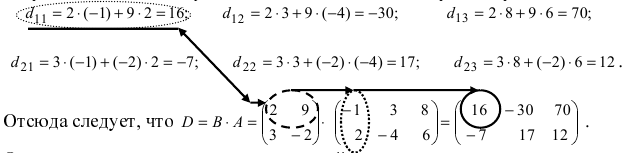
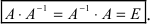
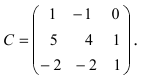
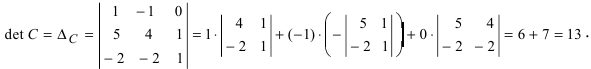
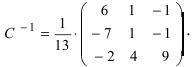
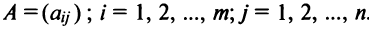
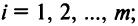
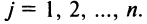

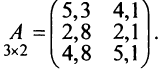
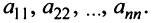

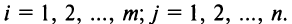
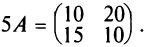
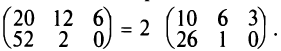
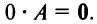
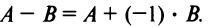
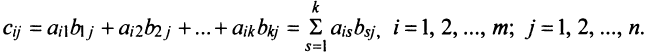
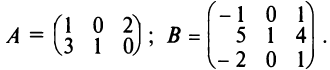
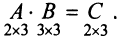
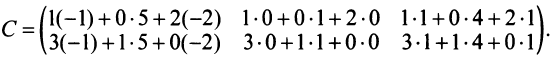
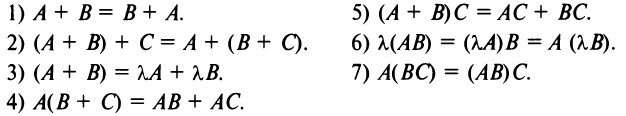
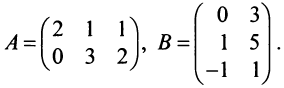
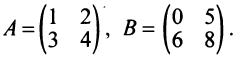
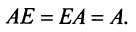
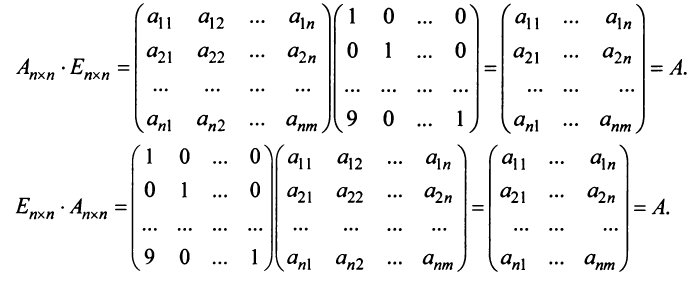
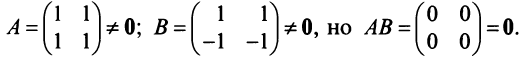
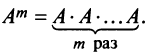
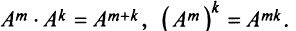
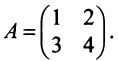
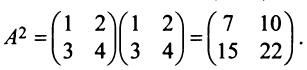
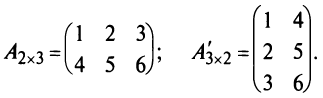

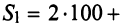
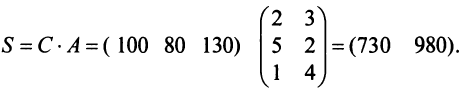

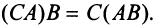

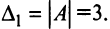
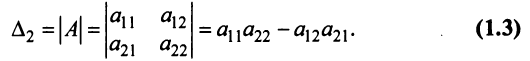
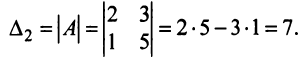
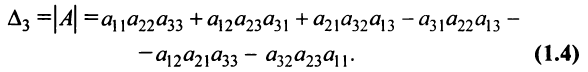

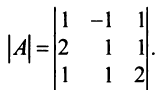


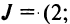

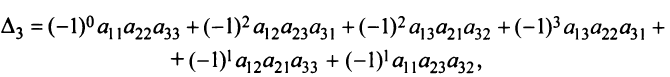
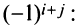

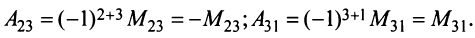
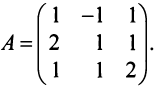
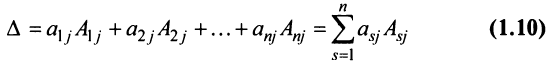
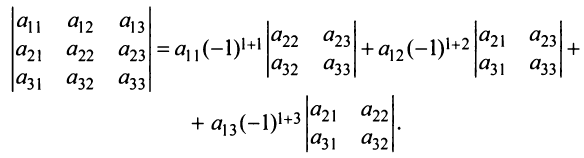

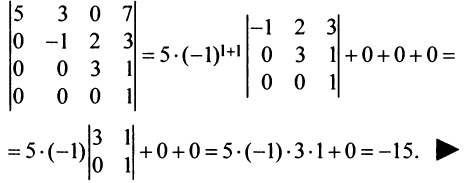
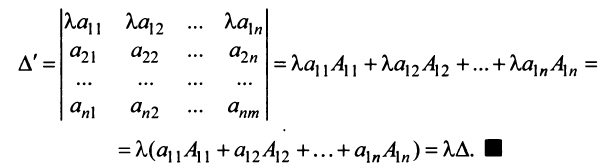
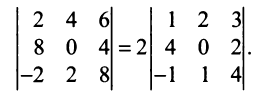
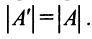
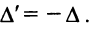

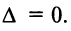
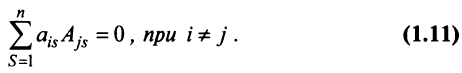
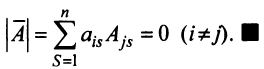
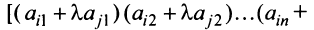
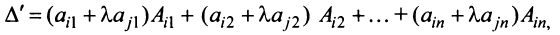
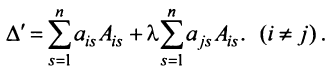
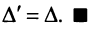
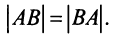
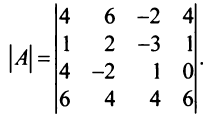
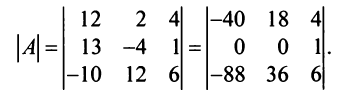
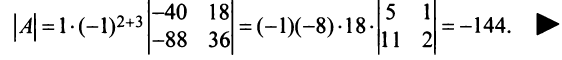

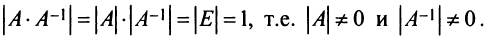
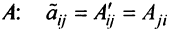
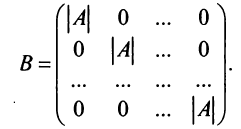
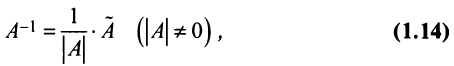

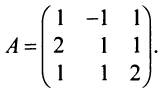
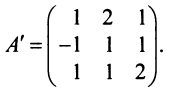
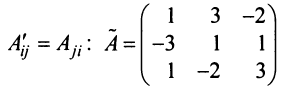
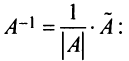
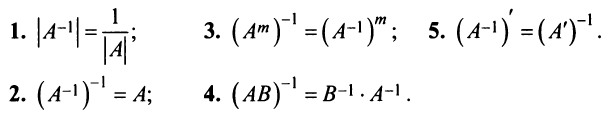
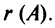
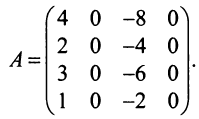

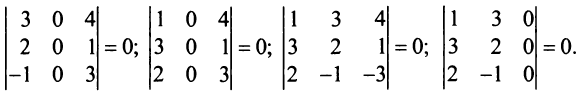

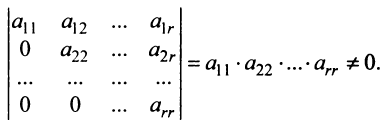
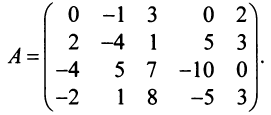
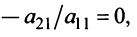
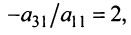
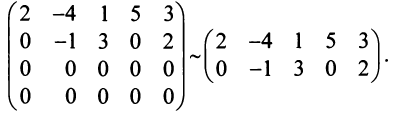

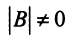
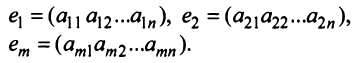
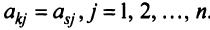
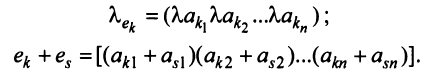
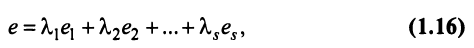
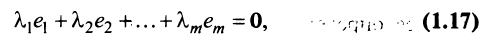
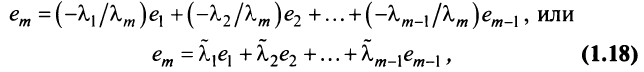
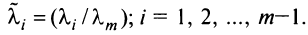


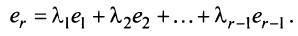


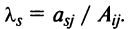
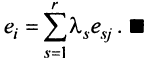
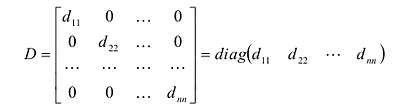
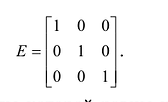
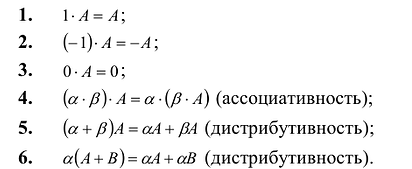
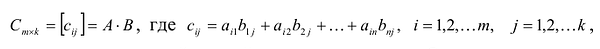
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;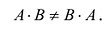
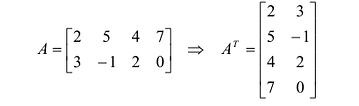
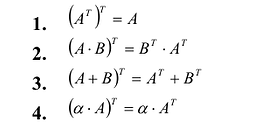
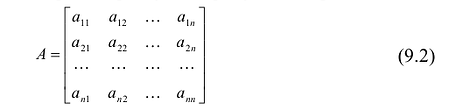
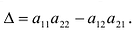
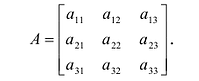
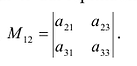
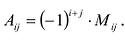
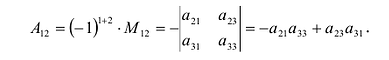
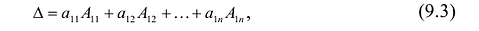
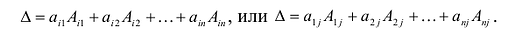
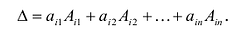
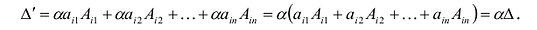
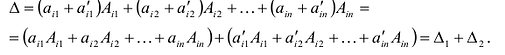

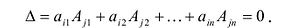
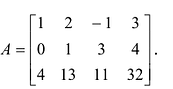
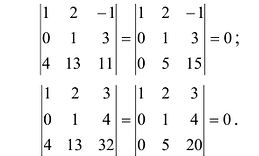

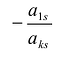 и т.д.;
и т.д.;



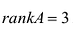
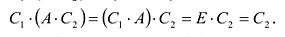
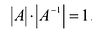
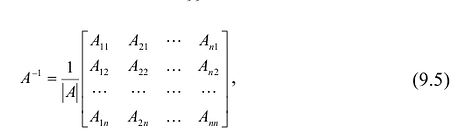
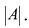

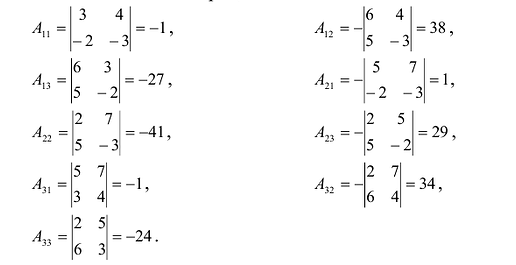
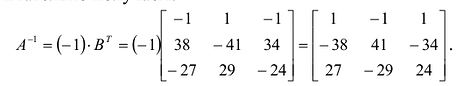


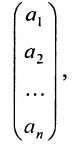
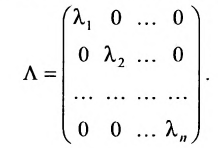
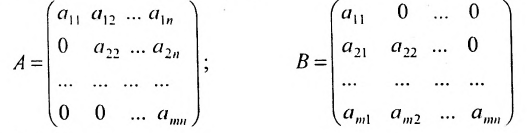

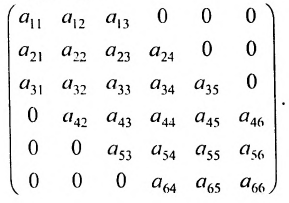
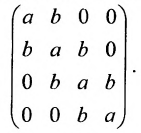




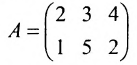

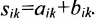
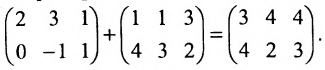
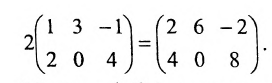
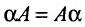 .
.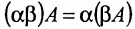 .
.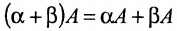 .
.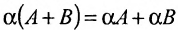 .
.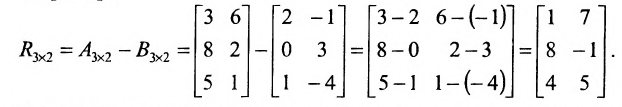
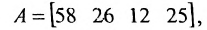
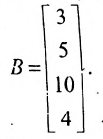
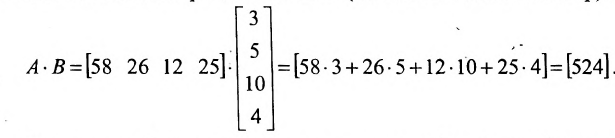

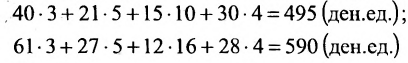
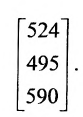
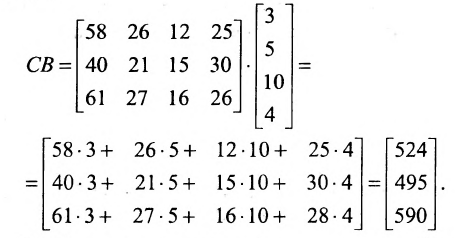
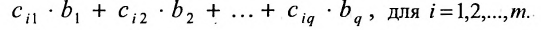


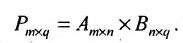
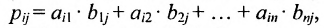
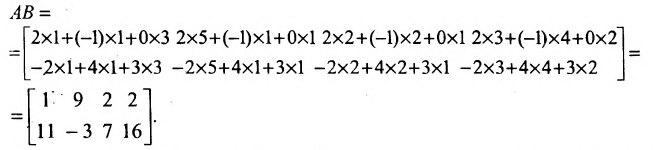
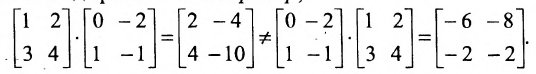
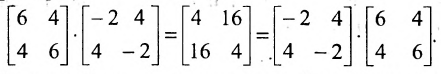
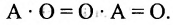
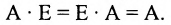

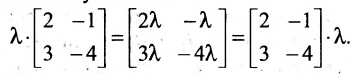
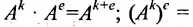
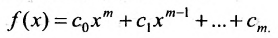
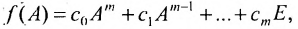
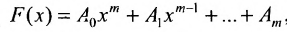
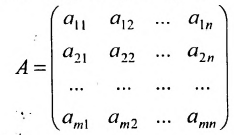
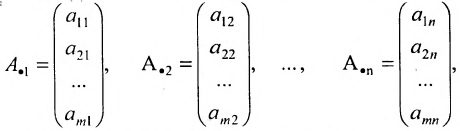
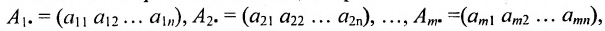
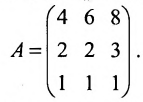


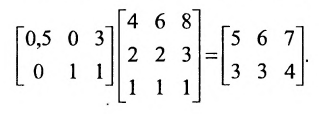
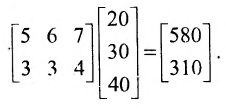
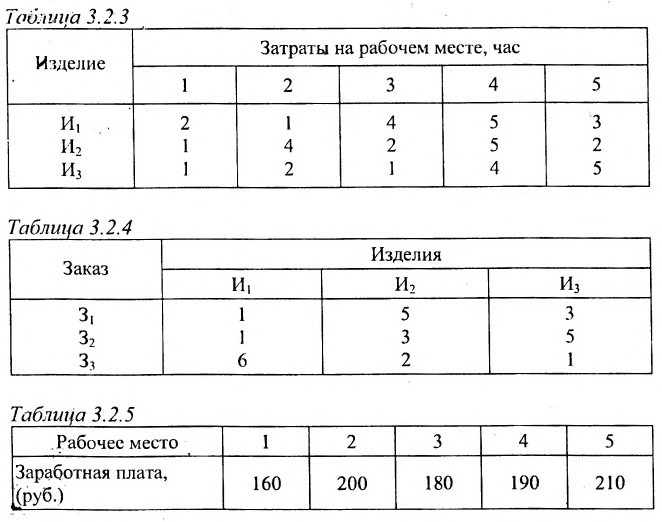
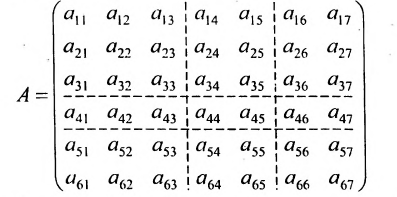
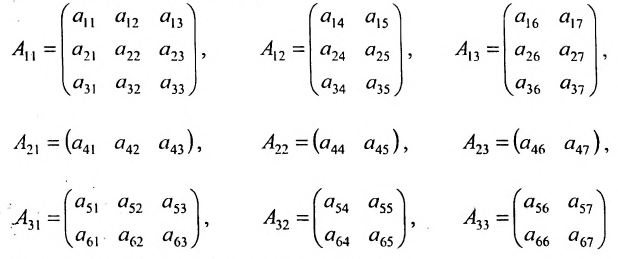
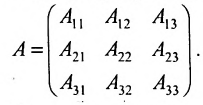
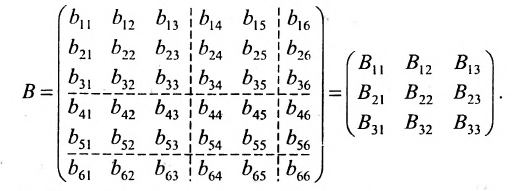
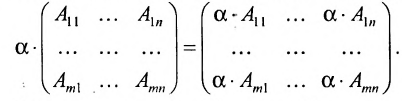
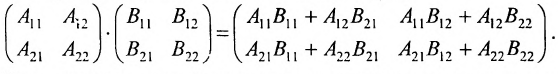
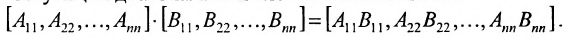
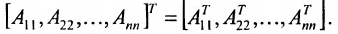
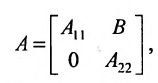
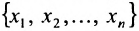
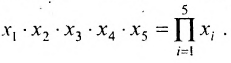
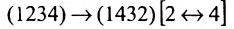

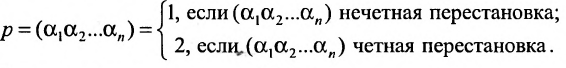
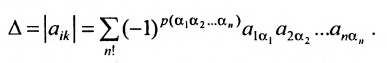
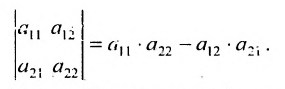
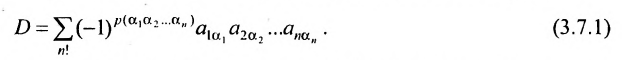
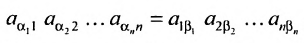
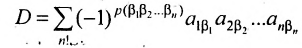
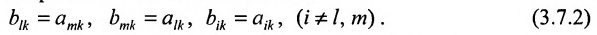
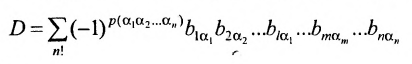
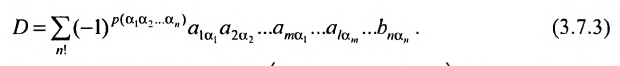
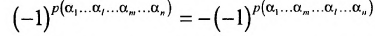
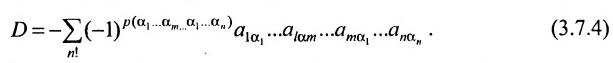
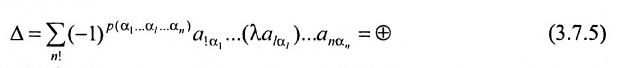
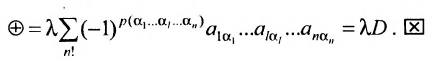
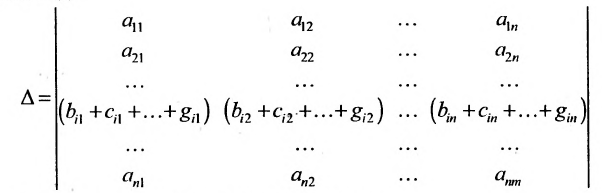
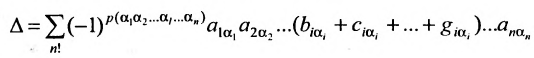
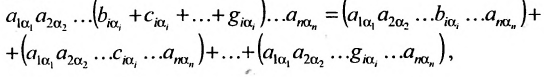
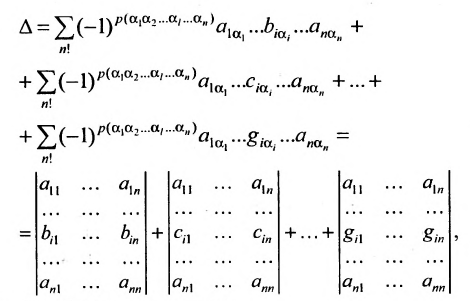

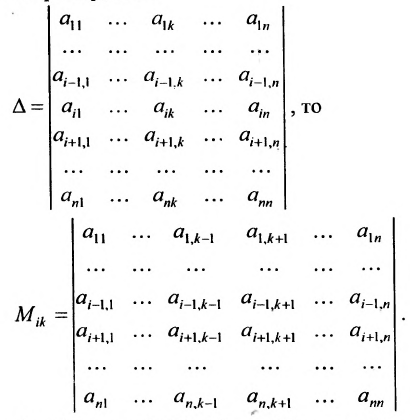

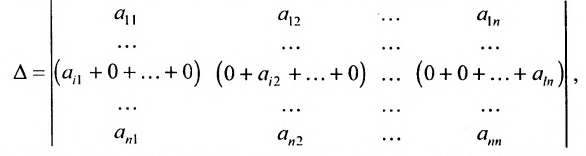

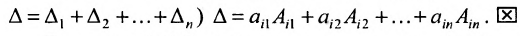

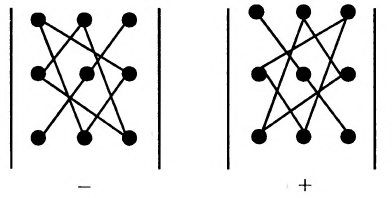
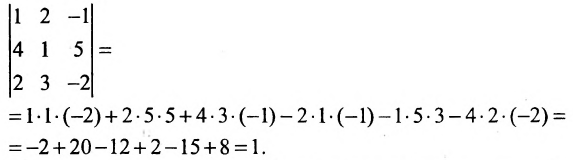

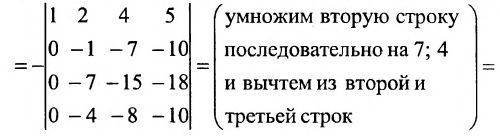

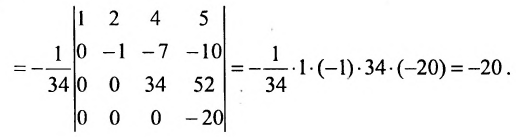
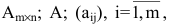
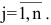
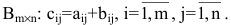
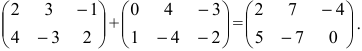
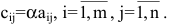
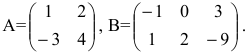
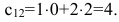
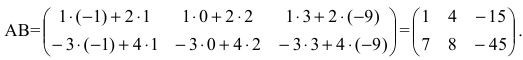
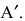
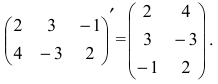

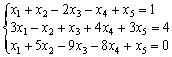

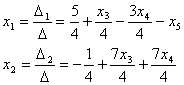
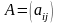
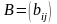
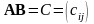
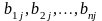

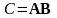
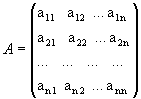
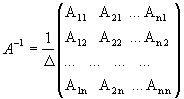

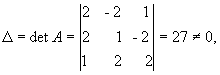
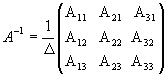


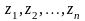


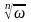
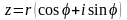
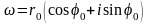
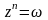
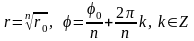
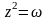
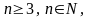

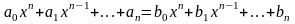
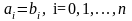

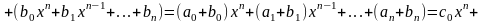

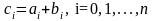

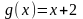
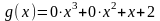
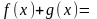
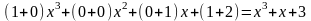
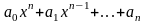
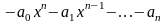
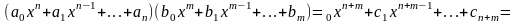
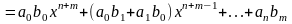
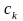
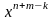
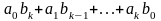
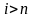
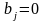
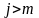

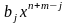
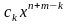

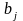
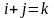
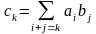
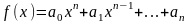
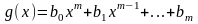
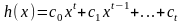


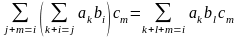


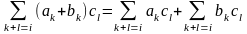
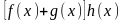



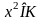
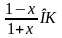

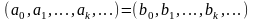
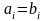

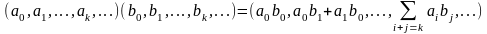
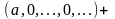

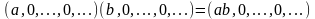
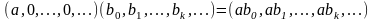
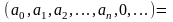

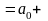

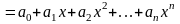
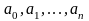
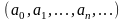

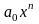
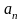







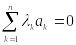

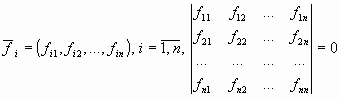

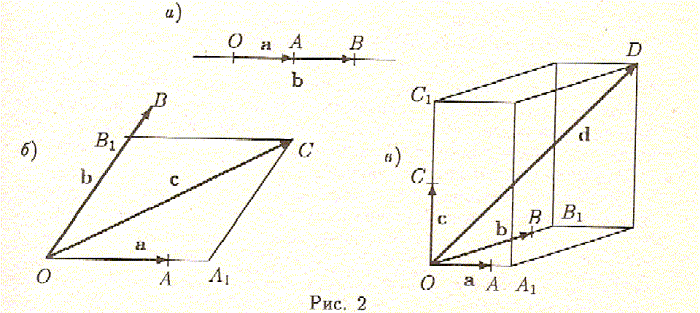

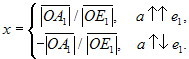


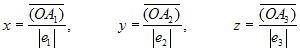

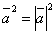

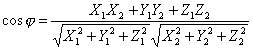


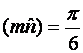



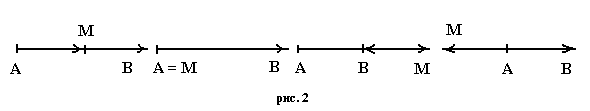
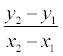

 Ответы на вопросы по заказу заданий по матрицам:
Ответы на вопросы по заказу заданий по матрицам:





















































































































 линейных уравнений с
линейных уравнений с  неизвестными имела ненулевое решение, необходимо и достаточно, чтобы
неизвестными имела ненулевое решение, необходимо и достаточно, чтобы 































