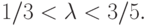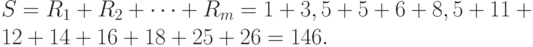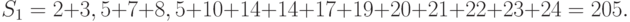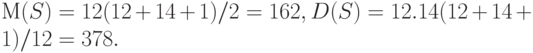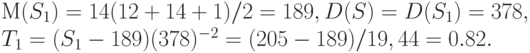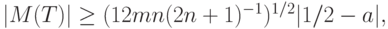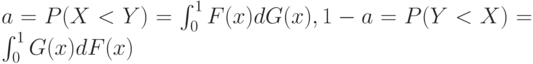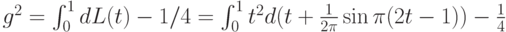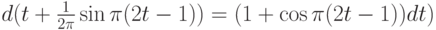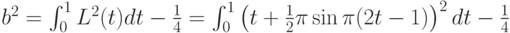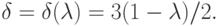А. Ранжирование
качественных признаков
Пример 1.
Испытуемому
предлагается задание, в котором семь
личностных качеств необходимо упорядочить
(проранжировать) в двух столбцах: в левом
столбце в соответствии с особенностями
его «Я реального», а в правом столбце в
соответствии с особенностями его «Я
идеального». Результаты ранжирования
даны в таблице 2.
Таблица 2.
-
Я
реальноеКачества
личностиЯ
идеальное7
ответственность
1
1
общительность
5
3
настойчивость
7
2
энергичность
6
5
жизнерадостность
4
4
терпеливость
3
6
решительность
2
Б. Ранжирование
количественных признаков
Пример 2.
В результате
диагностики невроза у пяти испытуемых
по методике К.Хека и Х. Хесса были получены
следующие баллы: 24, 25, 37, 13, 12. Этому ряду
чисел можно проставить ранги двумя
способами:
-
большему числу в
ряду ставится больший ранг, в этом
случае получится: 3, 4, 5, 2, 1; -
большему числу в
ряду ставится меньший ранг: в этом
случае получится: 3, 2, 1, 4, 5.
4.2. Проверка правильности ранжирования
А. Формула для
подсчета суммы рангов по столбцу
(строчке)
Если
ранжируется N
чисел,
то сумма рангов расчитывается по формуле
(1.1):
1+2+3+…+N=N(N+1)/2
(1.1)
В
случае примера 1 число ранжируемых
признаков было равно N
=7,
поэтому сумма рангов, подсчитанная по
формуле (1.1), должна равняться 7(7+1)/2=28.
Сложим величины
рангов отдельно для левого и правого
столбца таблицы:
7 + 1 + 3+ 2 + 5 + 4 + 6 = 28
— для левого столбца и
1 + 5+ 7+ 6 + 4 + 3 + 2 = 28
— для правого столбца.
Суммы рангов
совпали.
Б.
Формула
для расчета суммы рангов в таблице
Ранжирование
по столбцам.
Пример
3. Результаты
тестирования двух групп испытуемых по
5 человек в каждой по методике
дифференциальной диагностики депрессивных
состояний В. А. Жмурова представлены в
таблице 3.
Таблица 3.
-
Номер
испытуемогоГруппа
1Группа
21
15
26
2
45
67
3
44
23
4
14
78
5
21
3
Задача: проранжировать
обе группы испытуемых как одну, т. е.
объединить выборки и проставить ранги
объединенной выборке, сохраняя, однако
различие между группами. Сделаем это
в таблице 4, причем так, что максимальной
величине будем ставить минимальный
ранг.
Таблица 4.
-
Номер
испытеумогоГруппа
1Ранги
Группа
2Ранги
1
15
8
26
5
2
45
3
67
2
3
44
4
23
6
4
14
9
78
1
5
21
7
3
10
Сумма
31
24
Поскольку у нас
получены суммы ранга по столбцам, то
общую сумму рангов можно получить,
сложив эти суммы: 31+24= 55.
Чтобы применить
формулу (1.1), нужно подсчитать общее
количество испытуемых — это 5+5=10.
Тогда по формуле
(1.1) получаем: 10(10+1)/2=55.
Ранжирование
прведено правильно.
Если в таблице
имеется большое число строк и столбцов,
то можно использовать модификацию
формулы (1.1)
Сумма
рангов в таблице
=
(kc+1)kc/2
, (1.2)
где
k
— число строк, с — число столбцов.
Вычислим сумму
рангов по формуле (1.2.) для нашего примера.
В таблице 2 имеется 5 строк и 2 столбца,
сумма рангов = ((5·2+1)·5·2)/2=55
Ранжирование
по строкам
Пример 4.
В предыдущем
примере добавили еще одну группу
испытуемых 5 человек
.
Таблица 5. Проведем
ранжирование по строчкам.
-
Номер
испытуемогоГруппа
1Ранги
Группа
2Ранги
Группа
3Рагни
1
15
1
26
2
37
3
2
45
2
67
3
24
1
3
44
3
23
1
55
3
4
14
1
78
3
36
2
5
21
2
3
1
33
1
Суммы
по столбцам8
10
12
В этой таблице
минимальному по величине числу ставится
минимальный ранг. Сумма рангов по каждой
строчке должна быть равна 6, поскольку
у нас ранжируется три величины: 1+2+3= 6. В
нашем случае так оно и есть. Теперь
просуммируем ранги по каждому столбцу
отдельно и сложим их.
Расчетная формула
общей суммы рангов для ранжирования по
строчкам для таблицы определяется по
формуле:
Сумма
рангов =
nc(c+1)/2,
(1.3.)
где
n
– количество испытуемых в столбце, с —
количество столбцов (групп).
Проверим правильность
ранжирования для нашего примера.
Реальная сумма
рангов в таблице 8+10+12= 30
По формуле (1.3):
5·3·(3+1)/2=30.
Следовательно,
ранжирование проведено правильно.
Случай одинаковых
рангов
Ранжирование
качественных признаков
А.
Ранжирование качественных признаков
Модифицируем
пример 1. и перепишем его в табл. 6.
Предположим, что при оценке особенностей
«Я реального» испытуемый считает, что
такие качества, как «настойчивость»
и «энергичность», должны иметь один и
тот же ранг. При проведении ранжирования
(столбец 1 табл. 6) этим качествам необходимо
проставить мысленные ранги (М.Р.), как
числа, обязательно идущие по порядку
друг за другом, и отметить эти ранги
круглыми скобками — ( ). Однако поскольку
эти качества, по мнению испытуемого,
должны иметь одинаковые ранги, то во
втором столбце табл. 6, относящемуся
к «Я реальному», следует поместить
среднее арифметическое рангов,
проставленных в скобках, т.е. (2 + 3)/2 = 2,5.
Таким образом, второй столбец табл. 6 и
будет окончательным итогом ранжирования
особенностей «Я реального», данным
испытуемым, а проставленные в этом
столбце ранги будут носить название
— реальные ранги (P.P.).
Аналогично при
ранжировании «Я идеального» испытуемый
считает, что такие качества, как
«общительность», «энергичность» и
«жизнерадостность», должны иметь один
и тот же ранг. Тогда при проведении
ранжирования (см. столбец 5 табл. 6) этим
качествам необходимо проставить
мысленные ранги, как числа, обязательно
идущие по порядку друг за другом, и
отметить эти ранги круглыми скобками
— ( ). Однако поскольку эти качества, по
мнению испытуемого, должны иметь
одинаковые ранги — то в четвертом
столбце табл. 6, относящемся к «Я
идеальному», следует поместить среднее
арифметическое рангов, проставленных
в скобках, т.е. (4 + 5 + 6)/3 = 5. Таким образом,
четвертый столбец таблицы 6 и будет
окончательным итогом ранжирования
особенностей «Я идеального», данным
испытуемым, а проставленные в этом
столбце ранги будут носить название —
реальные ранги. Подчеркнем еще раз, что
мысленные (условные) ранги, как числа,
должны располагаться друг за другом по
порядку, несмотря на то что ранжируемые
качества в таблице данных не находятся
рядом друг с другом.
Таблица 6.
|
Я |
Качества |
Я |
||
|
М.Р. |
P.P. |
P.P. |
М.Р. |
|
|
7 |
7 |
Ответственность |
1 |
1 |
|
1 |
1 |
Общительность |
5 |
(4) |
|
(2) |
2,5 |
Настойчивость |
7 |
7 |
|
(3) |
2,5 |
Энергичность |
5 |
(5) |
|
5 |
5 |
Жизнерадостность |
5 |
(6) |
|
4 |
4 |
Терпеливость |
3 |
3 |
|
6 |
6 |
Решительность |
2 |
2 |
Обозначения:
М.Р.
— мысленные, или условные, ранги; P.P.
— реальные ранги.
Проверим
правильность ранжирования во втором
столбце табл. 6, т.е. реальные ранги,
относящиеся к «Я реальному»:
1
+ 2,5 + 2,5 + 5 + 4 + 6 = 28.
По формуле (1.1)
сумма рангов также равняется 28.
Следовательно, ранжирование проведено
правильно.
Проверим правильность
ранжирования в четвертом столбце табл.
6, т.е. реальные ранги, относящиеся к «Я
идеальному»:
1 + 2 + 3 + 5 + 5 + 5 + 7 =
28.
По формуле (1.1)
сумма рангов также равняется 28.
Следовательно, ранжирование проведено
правильно.
Б. Ранжирование
количественных характеристик (чисел)
Ранжирование чисел
рассмотрим на примере.
Пример.
Психолог получил у 11 испытуемых следующие
значения показателя невербального
интеллекта: 113,102,123,122, 117, 117, 102, 108, 114, 102,
104. Необходимо проранжировать эти
показатели, и лучше всего это сделать
в таблице 7.
Таблица 7
|
Номер |
Показатели |
Мысленные |
Реальные |
|
1 |
113 |
6 |
6 |
|
2 |
102 |
(1) |
2 |
|
3 |
123 |
11 |
11 |
|
4 |
122 |
10 |
10 |
|
5 |
117 |
[8] |
8,5 |
|
6 |
117 |
[9] |
8,5 |
|
7 |
102 |
(2) |
2 |
|
8 |
108 |
5 |
5 |
|
9 |
114 |
7 |
7 |
|
10 |
102 |
(3) |
2 |
|
11 |
104 |
4 |
4 |
В примере
встретились две группы из равных чисел
(102, 102 и 102; 117 и 117), поскольку числа в
группах различны, то и скобки,
проставленные этим группам чисел, также
различны.
Проверим
правильность ранжирования по формуле
(1.1). Подставив исходные значения в
формулу, получим: 11·12/2 = 66. Суммируя
реальные ранги, получим:
6
+ 2 + 11 + 10 + 8,5 + 8,5 + 2 + 5 + 7 + 2 + 4 = 66.
Поскольку
суммы совпали, следовательно, ранжирование
проведено правильно.
Правила
ранжирования чисел таковы.
1.
Наименьшему (наибольшему) числовому
значению приписывается ранг 1.
2. Наибольшему
(наименьшему) числовому значению
приписывается ранг, равный количеству
ранжируемых величин.
3. Одинаковым по
величине числам должны проставляться
одинаковые ранги.
4. Если в ранжируемом
ряду несколько чисел оказались равными,
то им приписывается реальный ранг,
равный средней арифметической величине
тех рангов, которые эти числа получили
бы, если бы стояли по порядку друг за
другом.
5. Если в ранжируемом
ряду имеется две и больше групп равных
между собой чисел, то для каждой такой
группы применяется правило 4, и мысленные
ранги каждой группы заключаются в разные
скобки.
6. Общая сумма
реальных рангов должна совпадать с
расчетной, определяемой по формуле
(1.1).
7. Не рекомендуется
ранжировать более чем 20 величин
(признаков, качеств, свойств и т.п.),
поскольку в этом случае ранжирование
в целом оказывается малоустойчивым.
При необходимости
ранжирования достаточно большого числа
объектов следует объединять их по
какому-либо признаку в достаточно
однородные классы (группы), а затем уже
ранжировать полученные классы (группы).
Наиболее часто к
измерениям, полученным в ранговой шкале,
применяются коэффициенты корреляции
Спирмена и Кэндалла, и, кроме того,
используются разнообразные критерии
различий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
U-критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя независимыми выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30).
Он считается непараметрическим эквивалентом двухвыборочного независимого t-критерия .
Вот несколько примеров, когда вы можете использовать U-критерий Манна-Уитни:
- Вы хотите сравнить зарплату пяти выпускников университета А с зарплатой пяти выпускников университета Б. Распределение зарплаты не является нормальным.
- Вы хотите узнать, различается ли потеря веса для двух групп: 12 человек, использующих диету А, и 10 человек, использующих диету Б. Потеря веса не распределяется нормально.
- Вы хотите знать, отличаются ли баллы 8 учеников в классе A от результатов 7 учеников в классе B. Баллы не распределены нормально.
В каждом примере у вас есть две группы, которые вы хотите сравнить, распределение выборки не является нормальным, а размеры выборки малы.
Таким образом, U-критерий Манна-Уитни подходит, если выполняются следующие предположения.
Предположения U-критерия Манна-Уитни
Прежде чем проводить U-критерий Манна-Уитни, необходимо убедиться, что выполняются следующие четыре предположения:
- Порядковая или непрерывная. Анализируемая переменная является порядковой или непрерывной. Примеры порядковых переменных включают пункты Лайкерта (например, 5-балльная шкала от «полностью не согласен» до «полностью согласен»). Примеры непрерывных переменных включают рост (измеряется в дюймах), вес (измеряется в фунтах) или экзаменационные баллы (измеряются от 0 до 100).
- Независимость: все наблюдения обеих групп независимы друг от друга.
- Форма: формы распределений для двух групп примерно одинаковы.
Если эти предположения соблюдены, то можно переходить к проведению U-критерия Манна-Уитни.
Как провести U-тест Манна-Уитни
Чтобы провести U-критерий Манна-Уитни, мы следуем стандартной пятиступенчатой процедуре проверки гипотез :
1. Сформулируйте гипотезы.
В большинстве случаев U-тест Манна-Уитни выполняется как двусторонний тест. Нулевая и альтернативная гипотезы записываются как:
H 0 : две популяции равны
H a : две популяции не равны
2. Определите уровень значимости для гипотезы.
Определите уровень значимости. Распространенные варианты: .01, .05 и .1.
3. Найдите тестовую статистику.
Тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборки 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборки 1 и 2 соответственно.
В приведенных ниже примерах подробно показано, как найти эту тестовую статистику.
4. Отклонить или не отклонить нулевую гипотезу.
Используя статистику теста, определите, можете ли вы отклонить или не отклонить нулевую гипотезу на основе уровня значимости и критического значения, найденных в U-таблице Манна-Уитни .
5. Интерпретируйте результаты.
Интерпретируйте результаты теста в контексте заданного вопроса.
Примеры проведения U-критерия Манна-Уитни
В следующих примерах показано, как проводить U-критерий Манна-Уитни.
Пример 1
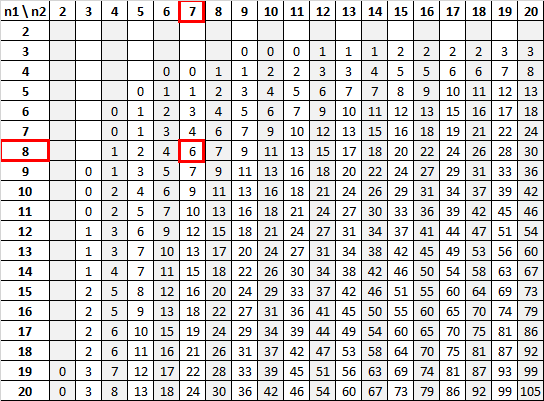
Мы хотим знать, эффективен ли новый препарат для предотвращения приступов паники. В общей сложности 12 пациентов были случайным образом разделены на две группы по 6 человек и назначены для получения нового препарата или плацебо. Затем пациенты записывают, сколько приступов паники у них было в течение одного месяца.
Результаты показаны ниже:
| НОВЫЙ ПРЕПАРАТ | плацебо | | — | — | | 3 | 4 | | 5 | 8 | | 1 | 6 | | 4 | 2 | | 3 | 1 | | 5 | 9 |
Проведите тест Манна-Уитни U, чтобы увидеть, есть ли разница в количестве панических атак у пациентов в группе плацебо по сравнению с группой нового препарата. Используйте уровень значимости 0,05.
1. Сформулируйте гипотезы.
H 0 : две популяции равны
H a : две популяции не равны
2. Определите уровень значимости для гипотезы.
Задача говорит нам, что мы должны использовать уровень значимости 0,05.
3. Найдите тестовую статистику.
Напомним, что тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборки 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборки 1 и 2 соответственно.
Чтобы найти R 1 и R 2 , нам нужно объединить наблюдения из обеих групп и ранжировать их в порядке от наименьшего к наибольшему:
| НОВЫЙ ПРЕПАРАТ | плацебо | | — | — | | 3 | 4 | | 5 | 8 | | 1 | 6 | | 4 | 2 | | 3 | 1 | | 5 | 9 |
Общая выборка: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Ранги: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12
R 1 = сумма рангов для выборки 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = сумма рангов для выборки 2 = 1,5+3+6,5+10+11+12 = 44
Затем мы используем наши размеры выборки n 1 и n 2 вместе с нашей суммой рангов R 1 и R 2 , чтобы найти U 1 и U 2 .
U 1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Наша тестовая статистика меньше U 1 и U 2 , что равно U = 13.
Примечание. Мы также можем использовать калькулятор критерия U Манна-Уитни , чтобы найти, что U = 13.
4. Отклонить или не отклонить нулевую гипотезу.
Используя n 1 = 6 и n 2 = 6 с уровнем значимости 0,05, U-таблица Манна-Уитни говорит нам, что критическое значение равно 5:
Поскольку наша тестовая статистика (13) больше нашего критического значения (5), мы не можем отвергнуть нулевую гипотезу.
5. Интерпретируйте результаты.
Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств, чтобы сказать, что количество приступов паники, испытываемых пациентами в группе плацебо, отличается от группы, принимавшей новое лекарство.
Пример 2
Мы хотим знать, помогают ли занятия по 30 минут в день в течение одной недели учащимся лучше сдавать тест. В общей сложности 15 пациентов были случайным образом распределены в группу исследования или группу без исследования. Через неделю все студенты сдают один и тот же тест.
Результаты тестов для двух групп показаны ниже:
| ИССЛЕДОВАНИЕ | БЕЗ ИССЛЕДОВАНИЯ | | — | — | | 89 | 88 | | 92 | 93 | | 94 | 95 | | 96 | 75 | | 91 | 72 | | 99 | 80 | | 84 | 81 | | 90 |
Проведите U-критерий Манна-Уитни, чтобы увидеть, есть ли разница в результатах тестов для исследуемой группы по сравнению с группой без исследования. Используйте уровень значимости 0,01.
1. Сформулируйте гипотезы.
H 0 : две популяции равны
H a : две популяции не равны
2. Определите уровень значимости для гипотезы.
Задача говорит нам, что мы должны использовать уровень значимости 0,01.
3. Найдите тестовую статистику.
Напомним, что тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборки 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборки 1 и 2 соответственно.
Чтобы найти R 1 и R 2 , нам нужно объединить наблюдения из обеих групп и ранжировать их в порядке от наименьшего к наибольшему:
| ИССЛЕДОВАНИЕ | БЕЗ ИССЛЕДОВАНИЯ | | — | — | | 89 | 88 | | 92 | 93 | | 94 | 95 | | 96 | 75 | | 91 | 72 | | 99 | 80 | | 84 | 81 | | 90 |
Общая выборка: 72 , 75 , 80 , 81 , 84 , 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Ранги: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = сумма рангов для выборки 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = сумма рангов для выборки 2 = 1+2+3+4+6+11+13 = 40
Затем мы используем наши размеры выборки n 1 и n 2 вместе с нашей суммой рангов R 1 и R 2 , чтобы найти U 1 и U 2 .
U 1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Наша тестовая статистика меньше U 1 и U 2 , что равно U = 12.
Примечание. Мы также можем использовать калькулятор критерия U Манна-Уитни , чтобы найти, что U = 12.
4. Отклонить или не отклонить нулевую гипотезу.
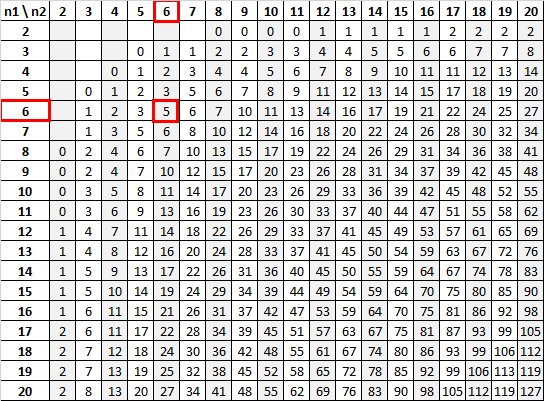
Используя n 1 = 8 и n 2 = 7 с уровнем значимости 0,01, U-таблица Манна-Уитни говорит нам, что критическое значение равно 6:
Поскольку наша тестовая статистика (12) больше нашего критического значения (6), мы не можем отвергнуть нулевую гипотезу.
5. Интерпретируйте результаты.
Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств того, что результаты тестов студентов, которые учились, отличаются от результатов тестов студентов, которые не учились.
Дополнительные ресурсы
Калькулятор критерия Манна-Уитни U
Таблица U Манна-Уитни
Как выполнить U-тест Манна-Уитни в Excel
Как выполнить U-тест Манна-Уитни в R
Как выполнить U-тест Манна-Уитни в Python
Как выполнить U-тест Манна-Уитни в SPSS
Как выполнить U-тест Манна-Уитни в Stata
Лекция 16-17.
9.3. Непараметрический метод для сравнение нескольких групп. Критерий Крускала-Уоллиса.
Для сравнения нескольких выборок ранее мы использовали дисперсионный анализ, который применим только в том случае, когда данные подчиняются нормальному закону распределения. В случае когда это условие не соблюдается необходимо воспользоваться непараметрическим аналогом дисперсионного анализа – а именно критерием Крускала-Уоллиса.
Критерий Крускала-Уоллиса представляет собой обобщение критерия Манна-Уитни. При использовании критерия Крускала-Уоллиса необходимо сначала упорядочить по возрастанию все значения вне зависимости от того, какой выборке они принадлежат. Каждому значению присваивается ранг соответствующий его месту в упорядоченном ряду. Аналогично рассмотренным ранее другим непараметрическим критериям совпадающим значениям присваивают общий ранг, равный среднему тех мест, которые эти величины делят между собой в упорядоченном ряду. Затем вычисляют суммы рангов, относящихся к каждой группе, и для каждой группы определяют средний ранг. При отсутствии межгрупповых различий средние ранги групп должны оказаться близки. Если существует значительное расхождение средних рангов, то гипотезу об отсутствии различий между группами необходимо отвергнуть. Значение критерия Крускала-Уоллиса Н является мерой различия средних рангов.
Рассмотрим пример. Предположим, что у нас имеется всего три группы (для большего числа групп критерий можно обобщить автоматически), для которых известны результаты измерения некоторого признака. Численность групп составляет n1, n2 и n3 соответственно. Объединим значения из разных групп, упорядочим по возрастанию и каждому присвоим ранг. Вычислим сумму рангов для каждой группы – R1, R2 и R3. Найдем средние ранги: ,
и
.
Общее число наблюдений N = n1+n2+n3. Для объединенной группы рангами являются числа 1, 2, …, N и общая сумма рангов равна
1+2+…+(N-1)+N=
Тогда средний ранг R для объединенной группы равен
Теперь найдем величину D, равную
Величина D зависит от размеров групп. Чтобы получить показатель, отражающий их различия, следует поделить D на N(N + 1)/12. Полученная величина
является значением критерия Крускала-Уоллиса. Суммирование в приведенной формуле производится по всем группам.
Для нахождения H можно было бы просто перечислить все сочетания рангов, как это делалось для критериев Манна-Уитни и Уилкоксона. Однако сделать это практически очень трудно, так как число вариантов слишком велико. К счастью, если группы не слишком малы, распределение Н хорошо приближается распределением 2 с числом степеней свободы = k-1, где k — число групп. Тогда для проверки нулевой гипотезы нужно просто вычислить по имеющимся наблюдениям значение Н и сравнить его с критическим значением 2. В случае трех групп приближение с помощью 2 пригодно, если численность каждой группы не меньше 5. Для четырех групп – если общее число наблюдений не менее 10. Но если группы совсем малы, не остается ничего, кроме как обратиться к таблице точных значений распределения Крускала-Уоллиса.
Чтобы выяснить, одинаково ли действие нескольких методов воздействия, каждый из которых испытывается на отдельной группе, нужно проделать следующее.
-
Объединив все наблюдения, упорядочить их по возрастанию. Совпадающим значениям ранги присваиваются как среднее тех мест, которые делят между собой эти значения. При большом числе совпадающих рангов значение Н следует поделить на
где N — число членов всех групп, i — как обычно, число рангов в i-й связке, а суммирование производится по всем связкам.
-
Вычислить критерий Крускала-Уоллиса Н.
-
Сравнить вычисленное значение Н с критическим значением Т для числа степеней свободы, на единицу меньшего числа групп. Если вычисленное значение Н окажется больше критического, различия групп статистически значимы.
9.4. Непараметрическое множественное сравнение
Необходимость в проведении множественного сравнения возникает всякий раз, когда с помощью дисперсионного анализа (или его непараметрического аналога – критерия Крускала-Уоллиса) обнаруживается различие нескольких выборок. В этом случае и требуется установить, в чем состоит это различие. Ранее мы познакомились с параметрическими методами множественного сравнения. Они позволяют сравнить группы попарно и затем объединить их в несколько однородных наборов так, что различия между группами из одного набора статистически незначимы, а между группами из разных наборов – значимы. Кроме того, они позволяют сравнить все группы с контрольной.
Известные нам параметрические методы множественного сравнения легко преобразовать в непараметрические. Когда объемы выборок равны, для множественного сравнения используют нераметрические варианты критериев Ньюмена-Кейлса и Даннета. Когда же объемы выборок различны, применяется критерий Данна. Опишем кратко эти методы.
Начнем с критериев для выборок равного объема. Критерии Ньюмена-Кейлса и Даннета совпадают практически полностью, поскольку критерий Даннета есть просто вариант критерия Ньюмена-Кейлса для сравнения всех выборок с одной контрольной.
Формула для непараметрического варианта критерия Ньюмена-Кейлса:

где RA и RB – суммы рангов двух сравниваемых выборок, n – объем каждой выборки, l – интервал сравнения. Вычисленное q сравнивается с критическим значением в табл. критерия Ньюмена-Кейлса для бесконечного числа степеней свободы.
Значение непараметрического критерия Даннета определяется формулой:

где Rкон — сумма рангов контрольной выборки, а остальные величины те же, что в критерии q, а l равно числу всех выборок, включая контрольную. Значение q’ сравнивается с критическим значением для бесконечного числа степеней свободы.
Наконец, для сравнения выборок разного объема используется критерий Данна. Впрочем, ничто не мешает применить его и к выборкам одинакового объема. Значение критерия Данна:

где и
— средние ранги двух сравниваемых выборок, nA и nB – их объемы, а N – общий объем всех сравниваемых выборок.
Критические значения Q приведены в таблице. «Стягивающее» сравнение проводится как в критерии Ньюмена-Кейлса.
Критерием Данна можно воспользоваться и для сравнения с контрольной выборкой. При этом формула для Q остается прежней, только критические значения находятся уже по другой таблице.
9.5. Повторные измерения. Критерий Фридмана.
Если одна и та же группа больных последовательно подвергается нескольким методам лечения или просто наблюдается в разные моменты времени, применяют дисперсионный анализ повторных измерений. Но чтобы использование дисперсионного анализа было правомерно, данные должны подчиняться нормальному распределению. Если вы в этом не уверены, лучше воспользоваться критерием Фридмана – непараметрическим аналогом дисперсионного анализа повторных измерений.
Логика критерия Фридмана очень проста. Каждый больной ровно один раз подвергается каждому методу лечения (или наблюдается в фиксированные моменты времени). Результаты наблюдений у каждого больного упорядочиваются. Обратите внимание, что если раньше мы упорядочивали группы, то теперь мы отдельно упорядочиваем значения у каждого больного независимо от всех остальных. Таким образом, получается столько упорядоченных рядов, сколько больных участвует в исследовании. Далее, для каждого метода лечения (или момента наблюдения) вычислим сумму рангов. Если разброс сумм велик – различия статистически значимы.
Таблица 1.
|
Данные для расчета критерия Фридмана. |
||||
|
Больной |
Метод лечения |
|||
|
1 |
2 |
3 |
4 |
|
|
1 2 3 4 5 Сумма рангов |
1 4 3 2 1 11 |
2 1 4 3 4 14 |
3 2 1 4 3 13 |
4 3 2 1 2 12 |
В табл. 1 описаны результаты испытания 4 методов лечения на 5 больных. В таблице указаны не сами значения, а их ранги среди данных, относящихся к одному больному. Каждая строка, кроме последней, соответствует одному больному. Последняя строка содержит суммы рангов для каждого из методов лечения. Различие сумм невелико; не похоже, чтобы эффективность какого-то метода отличалась от эффективности других.
Теперь обратимся к табл. 2. Различие в эффективности методов выражено предельно четко – упорядочение одинаково для всех больных. Во всех случаях наиболее эффективным оказался первый метод лечения, следующим – третий, за ним четвертый, и наконец, наименее эффективным – второй.
Таблица 2
Данные для расчета критерия Фридмана |
||||
|
Метод лечения |
||||
|
Больной |
1 |
2 |
3 |
4 |
|
1 2 3 4 5 Сумма рангов |
4 4 4 4 4 20 |
1 1 1 1 1 5 |
3 3 3 3 3 15 |
2 2 2 2 2 10 |
Перейдем к количественному оформлению наших впечатлений. Критерий Фридмана сходен с критерием Крускала-Уоллиса и вычисляется следующим образом. Сначала рассчитаем среднюю сумму рангов, присвоенных одному методу. (Именно этой величине равнялась бы сумма рангов любого из методов, если бы они были в точности равноэффективны.) Затем вычислим сумму квадратов S отклонений истинных сумм рангов, полученных каждым из методов, от средней суммы.
Разберем это на примере данных из табл. 1 и 2. Для каждого больного средний ранг равен (1 + 2 + 3 + 4)/4 = 2,5. В общем случае при k методах лечения средний ранг равен
| Ранги | 1 | 2 | 3,5 | 3,5 | 5 | 6 | 7 | 8,5 | 8,5 | 10 | 11 | 12 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Элементы выборок | 0 | 1 | 2 | 2 | 3 | 5 | 6 | 7 | 7 | 11 | 13 | 14 | 15 |
| Номера выборок | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 1 |
| Ранги | 14 | 14 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Элементы выборок | 15 | 15 | 17 | 21 | 22 | 25 | 29 | 30 | 33 | 44 | 47 | 66 | 97 |
| Номера выборок | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
Хотя с точки зрения теории математической статистики вероятность совпадения двух элементов выборок равна 0, в реальных выборках экономических данных совпадения встречаются. Так, в рассматриваемых выборках, как видно из табл.1, два раза повторяется величина 2, два раза — величина 7 и три раза — величина 15. В таких случаях говорят о наличии «связанных рангов», а соответствующим совпадающим величинам приписывают среднее арифметическое тех рангов которые они занимают. Так, величины 2 и 2 занимают в объединенной выборке места 3 и 4, поэтому им приписывается ранг 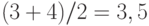

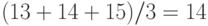
Следующий шаг — подсчет значения статистики Вилкоксона, т.е. суммы рангов элементов первой выборки
Подсчитаем также сумму рангов элементов второй выборки
Величина 



В соответствии с ранее проведенными расчетами 
Перейдем к расчету статистики Т. Согласно формуле (3)
Следовательно,
Поскольку 
Что будет, если поменять выборки местами, вторую назвать первой? Тогда вместо 
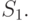
Таким образом, значения статистики критерия отличаются только знаком (можно показать, что это утверждение верно всегда). Поскольку в правиле принятия решения используется только абсолютная величина статистики, то принимаемое решение не зависит от того, какую выборку считаем первой, а какую второй. Для уменьшения объема таблиц принято считать первой выборку меньшего объема.
Продолжим обсуждение критерия Вилкоксона. Правила принятия решений и таблица критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (2). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?
Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (1) статистика T будет асимптотически нормальна с параметрами
![М(T) = ( 12mn )^{ ?} (1/2 - a) (m+n+1)^{ - ?} ,
D(T) = 12 [(n - 1) b^2 + (m - 1) g^2 + a(1 -a) ] (m+n+1)^{ - 1}](https://intuit.ru/sites/default/files/tex_cache/7f8adc5904c4bcce606c8cb95658ea96.png) |
( 5) |
Из формул (5) видно большое значение гипотезы
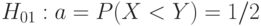 |
( 6) |
Если эта гипотеза неверна, то, поскольку 
а потому 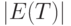
то
![D(T) le 12 [(n - 1) + (m - 1) + 1/4] (m+n+1)^{ - 1} le 12](https://intuit.ru/sites/default/files/tex_cache/ba8391d1fa7b39755713b0f3a06a8e98.png) |
( 7) |
Следовательно, вероятность отклонения гипотезы H01 , когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (6), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе
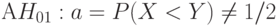 |
(
|
Если же гипотеза (6) верна, то статистика T асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой
![D(T) = 12 [(n - 1) b^2 + (m - 1) g^2 + 1/4 ] (m+n+1)^{-1}](https://intuit.ru/sites/default/files/tex_cache/bcae5545c281b36e1dd20e796bb30609.png) |
( 9) |
Гипотеза (6) является сложной, дисперсия (9), как показывают приводимые ниже примеры, в зависимости от значений 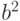
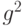
Приведем пример двух функций распределения 
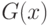
и 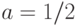
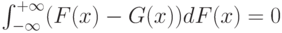 |
( 10) |
а потому естественно в качестве 
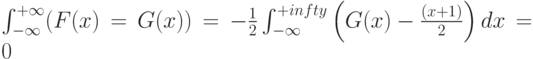 |
( 11) |
Это условие выполняется, если функция 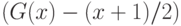
Пример 2. Пусть функции распределения 
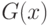
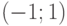
Тогда
Условие (11) выполнено, поскольку функция 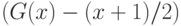

Поскольку
то
С помощью замены переменных 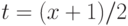
В правой части последнего равенства стоят табличные интегралы (см., например, справочник [14, с.71]. Проведя соответствующие вычисления, получаем, что в правой части стоит 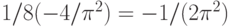
Перейдем к вычислению 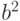
то
С помощью замены переменных 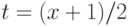
Проведя необходимые вычисления, получим, что
Следовательно, для рассматриваемых функций распределения нормированная и центрированная статистика Вилкоксона (см. формулу (4)) асимптотически нормальна с математическим ожиданием 0 и дисперсией (см. формулу (9))
Как легко видеть, дисперсия всегда меньше 1. Это значит, что в рассматриваемом случае гипотеза полной однородности (2) при проверке с помощью критерия Вилкоксона будет приниматься чаще, чем если она на самом деле верна.
На наш взгляд, это означает, что критерий Вилкоксона нельзя считать критерием для проверки гипотезы (2) при альтернативе общего вида. Он не всегда позволяет проверить однородность — не при всех альтернативах. Точно так же критерии типа хи-квадрат нельзя считать критериями проверки гипотез согласия и однородности — они позволяют обнаружить не все различия, поскольку некоторые из них «скрадывает» группировка.
Обсудим теперь, действительно ли критерий Вилкоксона нацелен на проверку равенства медиан распределений, соответствующих выборкам.
Пример 3. Построим семейство пар функций распределения 
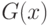

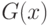
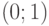
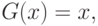

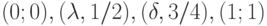


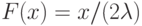
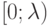
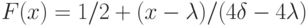
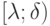
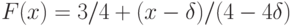
![[delta; 1]](https://intuit.ru/sites/default/files/tex_cache/99c26672f22f59edc51a4afea3549acd.png)
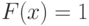

Очевидно, что медиана 

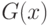
Согласно соотношению (9) для выполнения гипотезы (6) достаточно определить 
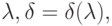
Вычисления дают
Учитывая, что