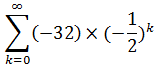Как найти сумму ряда для заданной точности - Исправление недочетов и поиск решений вместе с Examum.ru

Поскольку точное значение суммы ряда
удается вычислить далеко не всегда
(такие задачи были нами рассмотрены),
возникает проблема приближенного
вычисления суммы ряда с заданной
точностью.

Напомним, что
-ый
остаток рядаполучается из исходного рядаотбрасыванием первыхслагаемых:

Тогда, поскольку для сходящегося ряда

остаток сходящегося ряда равен разности
между суммой ряда и
-ой
частичной суммой:

и для достаточно больших
имеем
приближенное равенство

Из определения остатка ряда следует,
что абсолютная погрешность при замене
точного неизвестного значения суммы
его частичной суммойравна модулю остатка ряда:

Таким образом, если требуется вычислить
сумму ряда с заданной точностью
,
то нужно оставить сумму такого числаслагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:

Метод приближенного вычисления суммы
выбирается в зависимости от вида ряда:

если ряд положительный и может быть
исследован на сходимость по интегральному
признаку (удовлетворяет условиям
соответствующей теоремы), то для оценки
суммы используем формулу

;

если это ряд Лейбница, то применяем
оценку:

В других задачах можно использовать
формулу суммы бесконечно убывающей
геометрической прогрессии.

Задача №1. Сколько нужно взять
слагаемых ряда,
чтобы получить его сумму с точностью
0,01.

Решение.Прежде всего отметим, что
данный ряд сходится. Рассмотрим-ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:

Оценим этот ряд с помощью бесконечно
убывающей геометрической прогрессии.
Для этого заменим в каждом слагаемом
множитель
на,
при этом каждое слагаемое увеличится:

После вынесения общего множителя за
скобку, в скобке остался ряд, составленный
из членов бесконечно убывающей
геометрической прогрессии, сумму
которого мы и вычислили по формуле

Заданная точность будет достигнута,
если
будет удовлетворять условию

Решим неравенство, учитывая, что
—
целое.

При
имеем

В силу монотонности функции
,
неравенствобудет выполняться для всех.

Следовательно, если вместо точного
значения суммы мы возьмем первые пять
(или более) слагаемых, то погрешность
вычислений не превысит 0,01.

Ответ:
.

Задача №2. Оценить ошибку, получаемую
при замене суммы рядасуммой
первых 100 слагаемых.

Решение.Заметим, что данный ряд
является сходящимся и знакопеременным.
Оценивать будем ряд,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:

Рассмотрим ряд
.
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:

Вычислим несобственный интеграл:

погрешность вычислений можно оценить
по формуле

по условию
,
тогда.

Ответ:
.

Задача №3. Оценить ошибку,
получаемую при замене суммы рядасуммой
первых 10 слагаемых.

Решение.Подчеркнем еще раз, что
задача о приближенном вычислении суммы
имеет смысл только для сходящегося
ряда, поэтому, прежде всего отметим, что
данный ряд сходится. Поскольку исследуемый
ряд является знакопеременным со сложным
правилом изменения знака, то оценивать
придется, как и в предыдущем примере,
ряд из модулей данного ряда:

Используя тот факт, что
при любом значении аргумента, имеем:

Оценим остаток ряда:

Мы получили ряд, составленный из членов
бесконечно убывающей геометрической
прогрессии, в которой

его сумма равна:

Ответ:
.

Задача №4. Вычислить сумму рядас
точностью 0,01.

Решение.Данный ряд является рядом
Лейбница. Для оценки погрешности верна
формула:

другими словами, погрешность вычислений
меньше модуля первого отброшенного
слагаемого. Подберем номер
так, чтобы

При
имеем

Погрешность
,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:

Ответ:.

Соседние файлы в папке Ряды

Источник

Сумма ряда.

Пример 1:

Найти сумму ряда

Решение от преподавателя:

Пример 2:

Вычислить сумму ряда с точностью до Δ:

Решение от преподавателя:

: общий член ряда имеет вид — знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница) и погрешность при отбрасывании остатка ряда не превышает по абсолютной величине первый отбрасываемый член.

Вычисляем члены ряда:

Вычисления прекращаем, получаем сумму ряда с заданной точностью:

Пример 3:

Вычислить при любом натуральном n:

Решение от преподавателя:

Выразим сумму n-ого и (n+2)-го члена суммы:

Таким образом, имеем тождества:

Просуммируем все левыые и правые части:

Таким образом, мы имеем формулу для нахождения суммы ряда для любого n.

Пример 4:

Найдите сумму ряда:

Решение от преподавателя:

Степенной ряд в общем виде записывается следующим образом: ∑a_nxⁿ
где a_n — формула числовых коэффициентов. Для данного ряда:

Областью сходимости степенного ряда является интервал (-R;R), где:

R — радиус сходимости. Вычислим его:

Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-1;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд:

Это знакочередующийся числовой ряд который сходится согласно признаку Лейбница.

При x = -1
получаем ряд:

Это знакочередующийся числовой ряд, который сходится согласно признаку Лейбница.

То есть функциональный рядсходится при x∈[−1;1]

Чтобы вычислить сумму ряда, преобразуйте его следующим образом:

Во-первых, докажем, что данный ряд сходится. В самом деле, ряд
является знакочередующимся рядом, члены которого по модулю не возрастают и .

По теореме Лейбница данный ряд сходится к некоторому числу S

Пример 5:

Найти сумму ряда

Решение от преподавателя:

Пример 6:

Доказать, что при любом n > 1, сумма ряда больше 0,5 и меньше 0,75.

Решение от преподавателя:

Проверим для S_n

_{Таким образом, по методу математической индукции исходрное утверждение доказано.}

Пример 7:

Вычислить при любом натуральном n:

Решение от преподавателя:

Выразим сумму n-ого и (n+2)-го члена суммы:

Таким образом, имеем тождества:

Просуммируем все левыые и правые части:

Таким образом, мы имеем формулу для нахождения суммы ряда для любого n.

Пример 8:

Решение от преподавателя:

Пример 9:

Оценить ошибку, получаемую при замене суммы ряда суммой первых 100 слагаемых.

Решение от преподавателя:

Пример 10:

Найти сумму ряда:

Решение от преподавателя:

Предположим, что

Приведем правую сторону к общему знаменателю:

Приравниваем получившееся значение к первоночальному, получаем:

Знаменатели дробей равны, следовательно равны и числители:

Получаем систему уравнений:

Зная численные значения А и В, имеем:

Тогда сумма ряда равна:

Получаем верную формулу, следовательно:

Пример 11:

Сколько нужно взять слагаемых ряда , чтобы получить его сумму с точностью до 0,01?

Решение от преподавателя:

Погрешность суммы ряда не превышает по модулю первого отброшенного члена ряда. Поэтому находим искомое число членов ряда:

Поэтому начиная с k = 10-го члена ряда соответствующие члены ряда можно отбросить. Следовательно, необходимо взять m = 9 членов ряда, чтобы получить его сумму с точностью до 0,01.

Пример 12:

Найти сумму ряда:

Решение от преподавателя:

Используем формулу арифметической прогрессии:

Получим, что

Тогда имеем тождество:

Докажем верность для (n+1) равенства:

Значит, сумма такого ряда:

Пример 13:

Найти сумму ряда:

Решение от преподавателя:

Пример 14:

Найти сумму ряда:

Решение от преподавателя:

Пример 15:

Решение от преподавателя:

Пример 16:

Решение от преподавателя:

Пример 17:

Вычислить сумму ряда с заданной точностью ε.

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

22423 авторов готовы помочь тебе.
2402 онлайн

Источник

Подсказка (возможно не к этому примеру, но к сходящимся рядам в общем): double не резиновый, при сложении очень малых значений с очень большими (относительно, естественно) малое просто не входит в значимые разряды и отсекается. Складывать надо очень аккуратно по кускам (проверка S главного cо следующим членом ряда, если сильно разнятся, то завести 2ую сумму и в ней складывать до тех пор, пока не получится сумма, сравнимая с Sглавным, 2ая тоже может иметь такое неприятное явление, и, возможно надо заводить 3ю и т. д.).
Также почему условие while (a >= e)? Достаточно-ли только его?
z вычисляется верно? (при n=2 z д.б. 4! = 4*3*2*1 = 24, у нас z(1) = ??? непонятно чему, инициализации нет, ну пусть z начальное было б 1, тогда z(1)=2(верно), z(2)=2*(2+2) = 8 < 24 (неверно)).

Добавлено через 10 минут
Итого: попробуйте сначала z = z*(2n*(2n-1)), и инициализируйте его.

Не по теме:

И после этого ещё говорят, что прогерам не нужно знание математики и внутреннего представления типов данных. Мдя…

Источник

В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.

Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.

Сходящийся ряд

Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:

Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |a_n — a_n-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.

Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.

Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);

Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5^k.

Функцию f можно записать короче:

double f(int k)

{

return —32.0 * powf(—0.5, k);

}

Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.

float e;

printf(«e = «);

scanf_s(«%f», &e);

Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.

double previous, current;

double sum = 0;

int k = 0;

Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.

current = f(k);

sum += current;

k++;

Запись выражения sum += current; эквивалентна записи: sum = sum + current;

Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |a_n — a_n-1| > ε.

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

Сумма посчитана. Осталось вывести результат вычислений в консоль.

printf(«sum = %fn», sum);

В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:

#include <stdio.h>

#include <math.h>

#include <conio.h>

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

int main()

{

float e;

printf(«e = «);

scanf_s(«%f», &e);

double previous, current;

double sum = 0;

int k = 0;

current = f(k);

sum += current;

k++;

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

printf(«sum = %fn», sum);

_getch();

return 0;

}

Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.

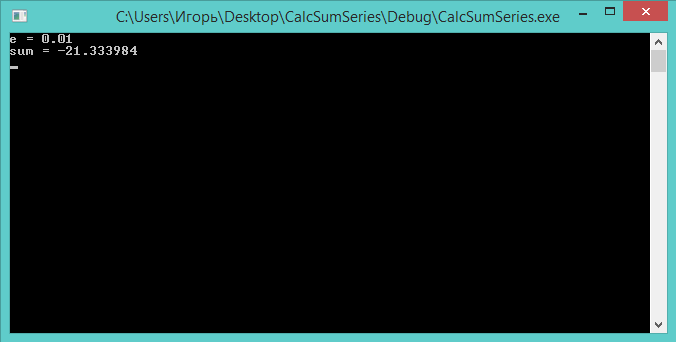
Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.

Скачать исходник

Источник