Рассмотрим
некоторые приемы нахождения суммы
функционального
ряда и области его сходимости к этой
сумме.
Нахождение
суммы ряда почленным интегрированием.
-
Пусть
дан ряд вида
.
По признаку Коши или
признаку
Даламбера область
сходимости определяется
неравенством
.
Если
,
то ряд
— расходящийся.
Если
,
то ряд
сходится условно (по признаку Лейбница).
Следовательно, область сходимости
находится из неравенства
.
Затем делаем
замену
в исходном ряде; получаем степенной ряд
с областью сходимости
.
Используем формулу для вычисления суммы
членов бесконечно убывающей геометрической
прогрессии со знаменателем
(12)
и
очевидное равенство
(13)
Учитывая,
что степенной ряд можно почленно
интегрировать по любому отрезку
,
целиком принадлежащему интервалу
сходимости, и используя формулу (13),
получаем
Заметим,
что так как ряд (12) сходится в граничной
точке t=-1,
то сумма ряда непрерывна в этой точке
(справа) и
.
Далее вычисляем интеграл (с переменным
верхним пределом), заменяем t
на
и получаем ответ.
-
Если
дан ряд вида
,
то следует либо
применить
теорему о почленном интегрировании
степенного ряда дважды, либо разложить
дробь на элементарные
и
вычислить сумму каждого ряда почленным
интегрированием.
Пример.
Найти сумму ряда
и указать область
его
сходимости к этой сумме.
Решение.
Данный ряд степенной. Находим его
интервал сходимости. По признаку Коши
имеем
.
Из неравенства находим
.
Исследуем поведение ряда в граничных
точках. При
—
расходящийся гармонический ряд. При
— условно сходящийся ряд по признаку
Лейбница. Следовательно, данный ряд
сходится при
.
Для нахождения суммы ряда сделаем замену
.
Получим геометрический ряд
,
сходящийся при
.
Используя равенство (13) и почленное
интегрирование степенного ряда, получаем:

Ответ:
для
.
Замечание.
Степенной ряд (10) сходится абсолютно и
равномерно на всяком отрезке, лежащем
внутри его интервала сходимости; ряд
(10) можно почленно интегрировать и
дифференцировать внутри его интервала
сходимости
,
т.е. если
то для
имеем
и
Задание
17. Найти
сумму ряда и указать область сходимости
к этой сумме.
Задача
1.
Решение.
Имеем
.
Найдем
сумму каждого из этих рядов в их области
сходимости. Сначала рассмотрим ряд
.
Используем
формулу для вычисления суммы членов
бесконечно убывающей геометрической
прогрессии
,
где
,
,
и равенство (13).Учитывая, что степенной
ряд можно почленно интегрировать на
любом отрезке
,
целиком принадлежащем интервалу
сходимости, получаем первую сумму:

Т.к.
ряд
сходится в граничной точке х=-1, то его
сумма непрерывна в этой точке:
.Значит,
при
всех
.
(14)
Аналогично
находим вторую сумму с учетом (14):
Таким
образом, сумма исходного ряда

Ответ:
,
Задача
2.
Решение.
Находим область сходимости функционального
ряда, применяя признак Даламбера
Область
сходимости определяется неравенством
,
или
.
Решая его, получаем
или
.
При
имеем
—
расходящийся ряд (т.к.
~
).
Следовательно, ряд сходится при
.
Сделаем замену
.
Получим ряд
с областью сходимости
.
Используя формулу (12):
равенство (13):
и почленное интегрирование на любом
отрезке, принадлежащем области сходимости,
получаем
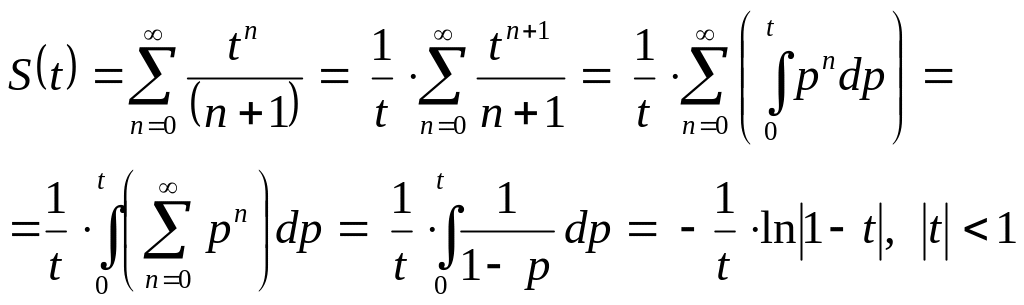
Заменяя
t
на
,
получаем сумму
Ответ:
,
.
Нахождение
суммы ряда почленным дифференцированием.
I.
Пусть дан ряд вида
.
Сначала
определяем область сходимости ряда,
например, по признаку Коши. Получаем
неравенство
.
Если
,
то ряд расходится, т.к. не выполнено
необходимое
условие
сходимости
.
Следовательно, область
сходимости
определяется неравенством
.
Затем делаем замену
и записываем ряд в виде суммы двух рядов
.
Для нахождения сумм этих рядов используем
формулу суммы членов бесконечно убывающей
геометрической прогрессии и очевидное
равенство
.
Учитывая,
что степенной ряд можно почленно
дифференцировать в любой точке интервала
сходимости, и используя равенство
,
получаем
Далее
вычисляем производную, делаем замену
и
записываем ответ.
II.
Если дан ряд вида
,
то вычисляем сумму трех рядов
,
и
,
причем при вычислении суммы ряда
применяем теорему о почленном
дифференцировании степенного ряда
дважды.
Задание
18. Найти
сумму ряда и указать область
сходимости
ряда к этой сумме.
Задача
3.
Решение.
а). Находим
область сходимости данного ряда по
признаку Даламбера
Отсюда
.
В граничных точках
ряд расходится, т.к. не выполнено
необходимое условие сходимости. Итак,
ряд сходится (и притом абсолютно) в
интервале (-1;1).
б).
Делаем в исходном ряде замену
и записываем в виде суммы двух рядов
Для
нахождения S(t)
достаточно найти суммы рядов
и
.
Учитывая,
что степенной ряд можно почленно
дифференцировать
в любой точке интервала сходимости,
получаем
.
И
в)
Заменяя
на
,
получаем
Ответ:
Задача
4.
Решение.
По признаку
Коши интервал сходимости
степенного
ряда определяется неравенством
,
т.е. ряд сходится в интервале (-1;1). Для
нахождения суммы ряда достаточно
представить ряд в виде суммы трех рядов
и найти суммы рядов:
,
где
применили один раз почленное
дифференцирование по x;
.
Т.к.
выше найденная на предыдущем шаге сумма
ряда
,
то еще раз применив почленное
дифференцирование по x
к ряду;
,
получаем
.Таким
образом, сумма исходного ряда равна
.
Ответ:
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
01.05.20221.51 Mб0Учебники 60167.doc
- #
01.05.20221.53 Mб0Учебники 60168.doc
- #
- #
- #
- #
- #
01.05.20221.56 Mб0Учебники 60172.doc
- #
- #
- #
Содержание:
- Понятие суммы ряда
- Вычисление суммы ряда почленным интегрированием
- Вычисление суммы ряда почленным дифференцированием
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 



По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 

Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Таким образом,
Заменяя 

Ответ.
Лекции:
- Метод Якоби
- Метод интегрирования
- Свойства функций, имеющих конечный предел
- Дифференциал длины дуги кривой. Формула парабол
- Дифференциальное уравнение Бернулли
- Область сходимости ряда
- Метод Ритца
- Разложение в ряд фурье функций
- Построение графиков функции с помощью производной
- Формулы двойного угла
ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ/PHYSICAL & MATHEMATICAL SCIENCE
УДК 519.642
ВЫЧИСЛЕНИЕ СУММЫ ЧИСЛОВОГО РЯДА МЕТОДОМ ИНТЕГРИРОВАНИЯ
CALCULATING THE SUM OF A NUMBER SERIESBY THE METHOD
OF INTEGRATION
©Апайчева Л. А.
канд. физ.-мат. наук, Нижнекамский химико-технологический институт (филиал) ФГБОУВПО «КНИТУ», г. Нижнекамск, Россия, lubovap@mail.ru
©Apaicheva L.
Nizhnekamsk Institute Of Chemical Technology (branch)FSFEI of HPE «KNRTU» Nizhnekamsk, Russia, lubovap@mail.ru
©ГалеевЭ. И.
Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО «КНИТУ» г. Нижнекамск, Россия, edvard_galeev@mail.ru
©Galeev E.
Nizhnekamsk Institute Of Chemical Technology (branch) FSFEI of HPE «KNRTU» Nizhnekamsk, Russia, edvard_galeev@mail.ru
Аннотация. Рассмотрен способ вычисления суммы числового ряда, использующий метод почленного интегрирования специально подобранного функционального ряда.
Abstract. A method for calculating the sum of a number series is considered, using the method of term-by-term integration of a specially selected functional series.
Ключевые слова: сумма ряда, метод интегрирования, рекуррентная формула.
Keywords: sum of the series, the method of integration, recurrent formula.
Ряды находят широкое применение в различных областях современной науки. В нашей работе [1] рассмотрены некоторые нестандартные подходы к решению задач по теме «Ряды». В практических задачах возникает также необходимость в вычислении суммы ряда, что в ряде случаев представляет особую сложность, так как решение таких задач требует изобретательности, догадки, творческого подхода.
Одной из важных целей данной работы является: дать возможность студентам более глубоко изучить курс математического анализа, способствовать развитию их интереса к математике, развитию творческого мышления, способностей применять теоретические знания в практической деятельности. Достижению этих целей помогает решение специально
№11 2017 г.
подобранных задач. Широкий выбор задач повышенной сложности имеется, например, в классическом сборнике задач [2].
В некоторых случаях удается подобрать функциональный ряд с известной суммой, почленное интегрирование которого приводит к нахождению суммы исходного ряда.
Рассмотрим пример. Вычислить сумму ряда
5
п=1
1^3…(2п — 1)(2п — 3) 2 • 4 … (2п — 2)(2п)
Решение. Сначала докажем соотношение
п
2
= I
I = I cos2nxdx = —
п (2п — 1)(2п — 3)…3^1 2 2п(2п — 2) … 4 • 2 ‘
Вычислим интеграл (1):
п
2
п
2
п
2
1= 1 cos^nxdx = 1 cos^n~-x cos2xdx = 0 0
п
2
= I cos2n 2x(1 — sin2x)dx = I cos2n 2xdx — I1.
(1)
(2)
Интеграл Ii будем вычислять по частям:
п
2
=I
cos2n 2х • sinx • sinxdx =
и = sinx, du = cosxdx dv = cos2n-2x • sinxdx 1
v = — —cos2′ 1X
n
2
2n—1
n
2
+
2^—1 Ic0s2UxdX== 2^—11
cos2nxdx.
sinx 2n — 1
2n—1 COS2′ 1X
(3)
Из соотношений (2) — (3) получаем
I cos2nxdx = I cos2n 2xdx — — I
J J 2n — 1J
cos2nxdx
Отсюда выводим рекуррентную формулу
0
0
0
I
1
0
0
0
п
п
п
2
2
0
0
0
и и и
2 2 2 f _ 2n—1f 7 (2n—1)(2n — 3)f _ .
I cos xdx =—— I cos 2xdx = —„ ^-—-I cos 4xdx = …
J 2n J 2n(2n -2) J
0 0 0 _n 3 … (2n — 1)(2n — 3)
= 2 ^ 2^4…(2n — 2)^2n ‘ (4)
Воспользуемся последней формулой для вычисления искомой суммы ряда. Имеем
1^3…(2п—1)(2п — 3)
2 • 4 … (2п — 2) • 2п
п=1
п п
т 2 2 т
2^ ..Г 2
= 2^(—1)П+1 J cos2nxdx = ^ J ^(—1)П+1 cos2nxdx. (5)
п ¿—I } п _
п=1 0 0 п=1
Вычислим интеграл в правой части равенства (5):
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
к
А = ¡^(С032Х — СОБ4Х + СОБ6Х — С058Х +—-+ ( — 1)п+гС032пХ + ••• )dx .
Подынтегральной функцией является геометрическая прогрессия со знаменателем
7 /■ 7 „ « СОБ2Х
Ц = С0Б2Х (соб2х < 1) и суммой-— .
1+ С05 X
Следовательно,
п п
2 2 Г С082Х Г ( 1
А = -rГdx= 1(1—r-)dx. (6)
7 1 + С0Э2Х ) V 1 + С052Х)
00
Вычислим
—
2
dx
Г dx / и „ Г dt
I -=т- = dt 7 1=1 -з-
J 1 + cos2x dx=—,cos2x = — J d , ,
0 1 + t2 1 + t2 0 (1 + t2)(1 + TTt2)
т
г dt 1 t
= ]—*=T2arct97i
0 2Л
0
Учитывая соотношения (5)-(6), находим искомую сумму ряда
y( 1)П+1^3.(2п — 1)(2п — 3) = 1—±
/-i( ) 2 • 4 … (2п — 2)(2п) Л
п=1
т
№11 2017 г.
Решение задач не примитивных — на применение формул, а требующих от студентов не только прочных знаний по программе, но и творческого подхода, побуждает студентов развивать свою математическую интуицию, логическое мышление, помогает подготовке к математическим олимпиадам.
Список литературы:
1. Апайчева Л. А., Шувалова Л. Е. Некоторые способы решения нестандартных задач по теме «Ряды» // Инновация наука. 2017. Т. 4. №4. С. 8-11.
2. Берман Г. Н. Сборник задач по курсу математического анализа. М.: Наука. 1967.
444 с.
Reference:
1. Apaicheva, L. A., & Shuvalova, L. Ye. (2017). Some ways of solving non-standard problems on the topic Rows. Innovatsionnaya nauka, 4, (4), 8-11
2. Berman, G. N. (1967). Collection of problems on the course of mathematical analysis. Moscow, Nauka, 444
Работа поступила Принята к публикации
в редакцию 07.10.2017 г. 11.10.2017 г.
Ссылка для цитирования:
Апайчева Л. А., Галеев Э. И. Вычисление суммы числового ряда методом интегрирования // Бюллетень науки и практики. Электрон. журн. 2017. №11 (24). С. 12-15. Режим доступа: http://www.bulletennauki.com/apaicheva (дата обращения 15.11.2017).
Cite as (APA):
Apaicheva, L., & Galeev, E. (2017). Calculating the sum of a number series by the method of integration. Bulletin of Science and Practice, (11), 12-15
Сумма ряда по-шагам
Результат
Примеры нахождения суммы ряда
- Сумма степенного ряда
- Факториал
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Сумма ряда
Содержание:
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 


Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Заменяя 

Ответ.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Высшая математика
-
Примеры решения рядов
Формулы и уравнения рядов здесь.
Пример. Исследование на сходимость и сумма ряда.
Дано: ряд
Найти: сумму ряда в случае его сходимости.
Решение.
Представим члены ряда в виде суммы двух слагаемых:
Получается, что n-я частичная сумма ряда может быть записана в виде:
Отсюда следует, что .
Ряд сходится. Сумма ряда равна .
Пример. Необходимый признак сходимости рядов.
Дано: ряд
Найти:
Проверить выполнение необходимого признака сходимости рядов.
Решение.
Необходимый признак сходимости рядов заключается в том, что если числовой ряд сходится, то
Как следствие, если ≠ 0, то ряд расходится.
Для данного в задаче числового ряда:
≠ 0. Ряд расходится.
Примеры. Достаточные признаки сходимости положительных рядов.
Дано: ряды
1)
2)
3)
4)
5)
6)
Найти:
Исследовать ряды на сходимость.
Решение.
1) Исходя из того, что ≤ при всех n и обобщенный гармонический ряд сходится, следует то, что ряд с меньшими членами сходящийся.
2) Исходя из того, что если выполняются условия: ln n ≥ 0 при n ≥ 1, то ≥ при n ≥ 1.
Обобщенный гармонический ряд расходится, следовательно, ряд с большими членами также расходится.
3) Из ряда выделим главную часть n-го члена: при n→∞ ∼ .
Заданный ряд и ряд ведут себя одинаково, так как .
Геометрический ряд сходится, значит, ряд также сходится.
4) Из ряда выделим главную часть n-го члена: при n→∞ ∼ .
Порядок 1, поэтому ряд сходится.
6) Из ряда выделяем главную часть n-го члена ряда:
при n→∞ ∼
Порядок , поэтому ряд расходится.
http://natalibrilenova.ru/summa-ryada/
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Как вычислить сумму ряда с помощью интеграла?
|
|
08/08/09 |
Как вычислить сумму ряда с помощью интеграла? Интересует либо общий случай: вот так уже пробовал:
|
|
|
|
|
ИСН |
Re: Как вычислить сумму ряда с помощью интеграла?
|
||
18/05/06 |
|||
|
|
|||
|
kiyanyn |
Re: Как вычислить сумму ряда с помощью интеграла?
|
|
25/07/11 |
Никак. Ну, не то чтобы непосредственно вычислять Другое дело, что человек почему-то решил, что такая замена даст точные результаты…
|
|
|
|
|
VoyagerEternal |
Re: Как вычислить сумму ряда с помощью интеграла?
|
|
08/08/09 |
мне не нужны точные результаты — нужны приблизительные с низкой погрешностью, при N > 16
|
|
|
|
|
svv |
Re: Как вычислить сумму ряда с помощью интеграла?
|
||
23/07/08 |
|||
|
|
|||
|
Klad33 |
Re: Как вычислить сумму ряда с помощью интеграла?
|
||
11/09/11 |
|
||
|
|
|||
|
VoyagerEternal |
Re: Как вычислить сумму ряда с помощью интеграла?
|
|
08/08/09 |
почти, методом тыка исправил ошибку: а как Вы вывели формулу?
|
|
|
|
|
ИСН |
Re: Как вычислить сумму ряда с помощью интеграла?
|
||
18/05/06 |
Ошибки не было, зато теперь есть. А формулу — видимо, Klad33 учился в секретной школе, где проходят геометрические прогрессии.
|
||
|
|
|||
|
Klad33 |
Re: Как вычислить сумму ряда с помощью интеграла?
|
||
11/09/11 |
Это слишком известный ряд. Я с ним постоянно имею дело по работе. — 30.11.2011, 17:31 — Верно так:
|
||
|
|
|||
|
VoyagerEternal |
Re: Как вычислить сумму ряда с помощью интеграла?
|
|
08/08/09 |
Ошибки не было, зато теперь есть. А формулу — видимо, Klad33 учился в секретной школе, где проходят геометрические прогрессии. ))) смешно
|
|
|
|
|
Lia |
Re: Как вычислить сумму ряда с помощью интеграла?
|
|
20/03/14 |
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы




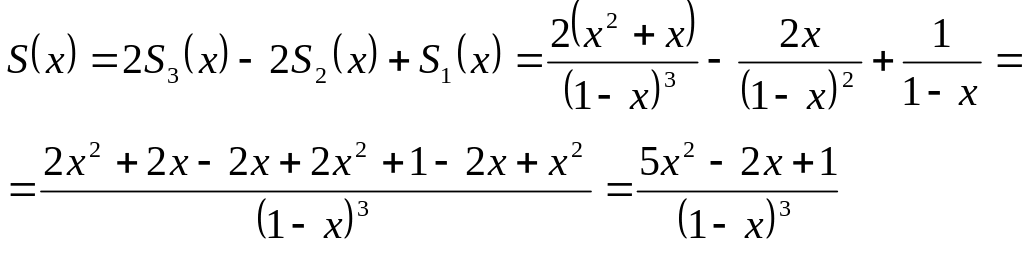




















 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем


































 , где
, где  — экспонента
— экспонента
 , а получается
, а получается 



