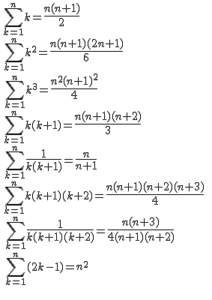|
Как сложить целые числа от 1 до N? Целые числа – это числа, не содержащие дробную или десятичную часть. Если в задаче требуется сложить определенное количество целых чисел от 1 до заданного значения N, то их не нужно складывать вручную. Вместо этого воспользуйтесь формулой (N(N+1))/2, где N — наибольшее число ряда. Окончательный ответ есть сумма всех целых чисел от 1 до данного N. Пример: (100(100+1))/2 = 100(101)/2 = (10100)/2 = 5050 Сумма всех целых чисел от 1 до 100 равна 5050. автор вопроса выбрал этот ответ лучшим В Рокотов 2 месяца назад Этот вопрос один из самых популярных в школьном образовании, даже несмотря на то, что сейчас на любое действие имеется онлайн калькулятор или иной электронный ресурс с подстановкой данных. Однако, более пригодится все-таки иметь представление о счете в диапазоне самому. Самая удобная формула нахождения суммы последовательного ряда в диапазоне от 1 до какого-то еще числа, назовем его N, такая: S =(n+1)*n/2; где N — наибольшее число ряда. Математику на пальцах не объяснишь, нужны примеры. Возьмем скажем последовательный ряд от единицы до пятнадцати., где нужно найти сумму диапазона от 1 до 15: (1+15)*15/2=120. Теперь стало более понятно. Удачи в будущих свершениях! -Irinka- 2 месяца назад Для того, чтобы облегчить жизнь — сделать расчеты более быстрыми и легкими, необходимо знать и пользоваться формулами. Для того, чтобы быстро и легко рассчитать сумму чисел, не производить сложение чисел в ручную, стоит воспользоваться формулой. Данная формула проверена ниже в ответе. В данной формуле буквой n обозначено максимальное число в данном ряду. Для того, чтобы понять формулу, можно произвести наглядный рассчет. За n условно возьмём число 6. Теперь подставляем зга, гения в формулу. S = 6×(6+1)/2 = 42/2 = 21. Теперь произведём сложение чисел последовательно без использования формулы. S = 6 + 5 + 4 + 3 + 2 + 1 = 21. Данные расчёты доказывают, что формула рабочая и ч её помощью произвести расчёт быстрее. Extrimal 2 месяца назад В математике данный вопрос можно встретить довольно часто. Многие считают, что это проще сделать вручную, складывая числа друг с другом по очереди. Однако если речь идет о больших числах, например если N=100, то проще воспользоваться формулой. Формула следующая Сумма равна (n+1) умножаем на n и делим на 2. Пробуем вычислить сумму, если n равно 100. 101*100/2 получаем 5050. КорнетОболенский 2 года назад Имеем ряд натуральных чисел. Первое число в ряду — единица, последнее N. Их сумму можно вычислить по формуле Для примера рассмотри сумму первых 10 натуральных чисел. В формулу вместо N поставим 10. Получим 10*(10+1)/2 = 55. Проверить несложно, посчитав эту сумму вручную. Сергей11110 3 года назад На самом деле, можно заметить, что ряд натуральных чисел образует арифметическую прогрессию с шагом 1. Сумма первых n членов арифметической прогрессии определяется формулой: S = (a1+an)*n/2; a1 = 1, а значит S = (n+1)*n/2 Это и есть сумма первых n натуральных чисел. Есть еще много способов ее посчитать, к примеру, написать программу на языке программирования (примерный код прилагаю): program a; var sum, i, n:longint; begin sum = 0; read(n); for i:=1 to n do begin sum:=sum+i; end; writeln(sum); end. Это код на языке программирования «Паскаль». Думаю, есть еще много способов посчитать сумму n первых натуральных чисел, но основные я перечислил. Просвет 7 лет назад Целые числа — это все числа, которые не дробные и не имеют десятично части, то есть 1, 2, 3, 10, 14, и так далее. Чтобы узнать их сумму, нужно ввести такой процесс с циклом: 1.. Задается N. A=0 S=0 2.. От 1 до N делать A=А+1 S=S+A В результате вы получите окончательный ответ S — сумма. (Вводить можно в паскале) MarkTolkien 6 лет назад Задача сложить ряд чисел от единицы до N не так сложна, но она требует слишком много времени. Упростить задачу призвана довольно простая формула: (N * (N + 1)) / 2 . Проверить формулу можем на простом примере вычисления суммы чисел от 1 до 5. 5 + 4 + 3 + 2 + 1 = 15. По формуле получаем 5 * (5 + 1) / 2 = 15. Чосик более года назад В данном примере мы обозначаем сумму чисел как S, а N — будет числом, до которого будет идти счет. То есть, N является самым большим числом среди всех. Рассчитываем сумму по формуле: Проверить правильность решения можно на малом числе. Допустим, N = 7. Можно просчитать сумму от 1 до 7. Выходит S = 1 +2 + 3 + 4 + 5 + 6 + 7 = 28. Теперь решим по формуле. S = 7 * (7+1)/ 2 = 7*8/2 = 56/2 = 28 владсандрович более года назад Если у нас идут натуральные числа вряд. При этом первым числом будет цифра 1, а последним N, то есть неизвестное. Тогда сумма их вычисляется вот такой вот формулой: (N * (N + 1)) / 2 . К примеру у вас в сумме идут 5 натуральных чисел. В формуле вместо N должна быть цифра 5. В итоге рассчитываем все так 5*(5+1)/2 =15. Степан БВ 2 месяца назад Сложить целые числа от 1 до N можно по формуле суммы арифметической прогрессии: S = (N * (N + 1)) / 2 где S — сумма чисел от 1 до N, N — последнее число в ряду. Например, если нужно сложить числа от 1 до 10, то S = (10 * (10 + 1)) / 2 = 55 Таким образом, сумма чисел от 1 до 10 равна 55. Natasha145 7 лет назад Это арифметическая прогрессия. Формула суммы N — первых членов такава: Знаете ответ? |
Загрузить PDF
Загрузить PDF
Если вы готовитесь к тестированию или просто хотите научиться быстро складывать числа, запомните, как суммировать целые числа от 1 до 

-
1
Определите арифметическую последовательность. Посмотрите на ряд чисел, которые вы хотите сложить. Чтобы воспользоваться формулой для суммирования целых чисел, убедитесь, что ряд чисел действительно является последовательностью, то есть каждое число возрастает на одну и ту же величину.[1]
- Например, ряд чисел 5, 6, 7, 8, 9 представляет собой последовательность, как и ряд 17, 19, 21, 23, 25.
- Ряд чисел 5, 6, 9, 11, 14 не является последовательностью, потому что числа возрастают на разные величины.
-
2
-
3
Найдите количество складываемых целых чисел. Чтобы суммировать целые числа от начального числа до
, необходимо найти общее количество складываемых чисел. Например, если вы хотите сложить целые числа от 1 до 200, общее количество чисел вычисляется так: 200+1 = 201.[2]
- Например, если нужно найти сумму целых чисел от 1 до 12, количество чисел: 12+1 = 13.
-
4
Найдите сумму целых чисел между двумя целыми числами, которые в расчете не участвуют. В этом случае вычтите 1 из
.[3]
- Например, чтобы найти сумму целых чисел между 1 и 100, вычтите 1 из 100 и получите 99.
Реклама
-
1
-
2
-
3
-
4
Пользуйтесь представленными формулами, чтобы найти сумму. Когда вы подставили нужно число в формулу, умножьте его на себя, прибавьте 1, 2 или 4 (в зависимости от формулы), а затем разделите результат на 2 или 4. [7]
- Пример 1: 100*101/2 = 10100/2 = 5050.
- Пример 2 (с четными числами): 20*22/4 = 440/4 = 110.
Реклама
Об этой статье
Эту страницу просматривали 191 897 раз.
Была ли эта статья полезной?
Формулы последовательностей:
где k — порядковый номер;
n — количество членов.
Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел.
1 вариант. Для того, чтобы определить сумму 5-ти последовательных чисел, следует умножить на 5 число, находящее посередине:
(х — 2) + (х — 1) + (х) + (х + 1) + (х + 2) = 5х,
в данном выражении х — число, находящееся посередине.
Например, сумма 30 + 31 + 32 + 33 + 34 будет равна 32 х 5 = 160
2 вариант. Чтобы найти сумму 5-ти последовательных чисел, нужно:
— умножить на 5 наибольшее число;
— из полученного произведения вычесть 10.
Возьмем, к примеру, те же 5 последовательных цифр 30,31,32,33,34
Дальше: 34 х 5 = 170
170 — 10 = 160
3 вариант. Чтобы найти сумму 5 последовательных чисел, можно:
— умножить на 5 наименьшее число;
— К полученному результату прибавить 10.
Взяв в качестве примера предыдущую последовательность:
30 х 5 = 150
150 + 10 = 160
Чтобы вычислить сумму 4-х последовательных чисел, нужно:
— умножить наибольшее число на 4;
— из полученного произведения вычесть 6.
Чтобы определить сумму 6 последовательных чисел, необходимо:
— умножить на 6 наибольшее число;
— от результата отнять 15.
Чтобы рассчитать сумму 7 последовательных чисел, нужно:
— умножить на 7 наибольшее число;
— вычесть из полученного произведения 21.
Чтобы вычислить сумму 8 последовательных чисел:
— умножим на 8 наибольшее число;
— из произведения вычесть 28.
Чтобы сложить любое количество как четных, так и нечетных последовательных чисел, нужно:
— сложить первое и последнее числа последовательности;
— полученный результат делим на 2;
— затем умножаем на число последовательных чисел, что выразим формулой:
n х (a+b)/2.
Чтобы быстро и правильно рассчитать сумму последовательности, воспользуйтесь онлайн калькулятором. Для этого вам нужно лишь выбрать последовательность и число членов последовательности.
Расчет суммы последовательности из приведенных последовательностей и количества членов
Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:
$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$
Приравниваем числитель последней дроби к числителю первой дроби:
$$ A(2n+3)+B(2n+1) = 1 $$
Раскрываем скобки:
$$ 2An + 3A + 2Bn + B = 1 $$
Теперь определяем находим неизвестные коэффициенты:
$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$
После разложения общий член ряда записывается следующим образом:
$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} — frac{1}{2} frac{1}{2n+3} $$
Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$
$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$
$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$
$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$
$$ …………………………………. $$
$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$
$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$
| Замечание |
|
Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок. |
Итого, получаем:
$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$
$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$
Выносим дробь одну вторую $ frac{1}{2} $ за скобки:
$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$
$$ + … frac{1}{2n-1} — frac{1}{2n+1} + frac{1}{2n+1} — frac{1}{2n+3} bigg) = $$
Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:
$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$
Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:
$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$
$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$
Если вы готовитесь к экзамену или хотите научиться быстро складывать числа, этот материал для вас.
Как найти сумму чисел 1 до N?
Для сложения определенного количества целых чисел в диапазоне от 1 до заданного значения N используется формула: N⋅(N+1)2frac{Ncdot(N+1)}{2}. Где NN — наибольшее число ряда.
Как работать с последовательностью чисел
- Определите арифметическую прогрессию, проверив последовательность чисел, которые вы собираетесь суммировать. Чтобы применить формулу для вычисления суммы целых чисел, убедитесь, что ряд чисел является арифметической прогрессией, то есть каждое последующее число увеличивается на одно и то же значение.
Пример
Последовательности чисел 5,6,7,8,95, 6, 7, 8, 9 и 17,19,21,23,257, 19, 21, 23, 25 являются арифметическими прогрессиями. Однако ряд чисел 5,6,9,11,145, 6, 9, 11, 14 не является арифметической прогрессией, так как числа увеличиваются на различные значения.
- Определите значение N в последовательности. Чтобы применить формулу для вычисления суммы целых чисел от 1 до N, определите наибольшее целое число, которое вы подставите вместо N.
Пример
Если вам нужно вычислить сумму всех целых чисел от 1 до 100, то N=100N = 100, поскольку это наибольшее целое число в последовательности. Помните, что вы работаете только с целыми числами, следовательно, NN не может быть дробным (обычным или десятичным) или отрицательным числом.
- Определите количество целых чисел, которые нужно сложить. Для того чтобы получить сумму целых чисел от начального числа до N, необходимо знать общее количество чисел, которые нужно сложить.
Пример
Если требуется сложить целые числа от 11 до 200200, то общее количество чисел равно 200−1+1=200200 — 1 + 1 = 200. Если нужно найти сумму целых чисел от 11 до 1212, то количество чисел равно 12−1+1=1212 — 1 + 1 = 12.
- Найдите сумму целых чисел между двумя заданными значениями, не включая сами эти значения. Для этого нужно вычесть единицу из разности между наибольшим и наименьшим числами.
Пример
Чтобы найти сумму целых чисел между 11 и 100100, нужно вычесть единицу из 100−1100 — 1, что даст 9999.
Как использовать формулу для сложения целых чисел
- Сформулируйте уравнение для вычисления суммы последовательных целых чисел. Чтобы вычислить сумму последовательных целых чисел до определенного значения n, используйте следующую формулу: Сумма =N⋅(N+1)2= Ncdotfrac{(N+1)}{2}.
Пример
Чтобы вычислить сумму целых чисел от 11 до 100100, замените NN на 100100 : 100⋅(100+1)2100cdotfrac{(100+1)}{2}.
- Запишите формулу для вычисления суммы четных целых чисел. Если вы хотите вычислить сумму четных целых чисел в последовательности, начинающейся с 1, воспользуйтесь формулой: Сумма =N⋅(N+2)4= frac{Ncdot(N+2)}{4} , где NN — наибольшее четное число в последовательности.
Пример
Чтобы вычислить сумму четных чисел от 1 до 20, замените N на 20⋅(20+2)4frac {20cdot(20+2)}{4}.
- Запишите уравнение для вычисления суммы нечетных целых чисел. Если вы хотите вычислить сумму нечетных целых чисел, то сначала найдите n, прибавив 1 к наибольшему числу в последовательности. Затем используйте следующую формулу: Сумма =(n+1)⋅(n+1)4= frac{(n+1)cdot(n+1)}{4}.
Пример
Чтобы вычислить сумму нечетных чисел от 1 до 9, замените NN на 99: (9+1)⋅(9+1)4frac{(9+1)cdot(9+1)}{4}.
- Примените соответствующую формулу, чтобы найти сумму. Когда вы подставили нужное число в формулу, умножьте его на себя, прибавьте 1,21, 2 или 44 (в зависимости от формулы), а затем разделите результат на 22 или 44.
Пример 1
Чтобы найти сумму целых чисел от 1 до 100, используйте формулу Сумма =100⋅(100+1)2= frac{100cdot(100+1)}{2}. Умножьте 100 на 101, затем поделите на 2, чтобы получить ответ: 50505050.
Пример 2
Чтобы найти сумму четных чисел от 1 до 20, используйте формулу Сумма =20⋅224= frac{20cdot22}{4}. Умножьте 20 на 22, затем поделите на 4, чтобы получить ответ: 110110.