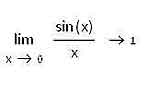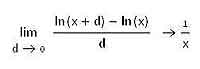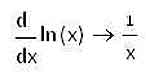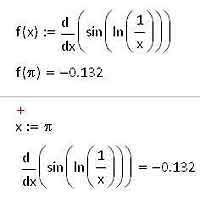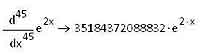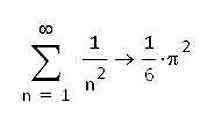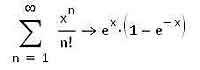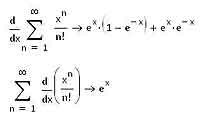Как найти сумму ряда в маткаде

Соседние файлы в папке TEXTBOOKS

• #
• #

  27.05.201534.74 Mб46Вержбицкий_В.Основы_числ_мет..pdf

• #

Всем привет.
Помогите пожалуйста решить задачу:
Дан ряд . Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда и найти величину погрешности при N= 10, , , , .

Порядок решения:
1. Найти сумму ряда S аналитически как предел частичных сумм ряда.
2. Используя функцию вычислить значения частичных сумм ряда при указанных значениях N.
3. Для каждого N вычислить величину абсолютной погрешности |S(N)-S| определить количество верных цифр в S(N).
4. Представить результаты в виде гистограммы.

Первый пунк на скрине, второй пункт не знаю как, подскажите пжл.
Спасибо.

Одно из самых впечатляющих достижений математики прошлых веков — это создание аппарата, позволившего количественно описать практически все законы природы, что и позволило физике стать самой передовой из всех наук. Естественно, MathCAD дает пользователю возможность воспользоваться всей мощью аппарата математического анализа (так принято называть курс дифференциального и интегрального исчисления в отечественных вузах) для решения задач. Сейчас мы с вами научимся пользоваться MathCAD’ом для вычисления пределов, производных, интегралов и прочих не слишком любимых студентами технических специальностей вещей.

Изучение математического анализа традиционно начинается с теории пределов. Вычисление пределов на практике, тем не менее, зачастую становится даже более сложной задачей, чем вычисление производных функций в точке или определенных интегралов. Несмотря на существование системы правил и теорем, которые позволяют вычислять пределы практически во всех случаях, эти вычисления, как правило, сопровождаются громоздкими выкладками и занимают очень много времени. Поэтому лучше переложить этот неблагодарный труд на плечи MathCAD’а, а самому заняться интерпретацией полученных результатов.

Вычислять пределы в среде MathCAD довольно просто. Найдите на панели Calculus операторы вычисления предела — там они, как и в математическом анализе, обозначаются с помощью слова lim. Всего в MathCAD’е присутствует три разных оператора вычисления предела: оператор вычисления предела в точке (двустороннего предела) и операторы правостороннего и левостороннего пределов. Для вычисления предела соответствующего типа нужно выбрать один из операторов, ввести точку и переменную, для которых мы будем вычислять предел, а также подкоренное выражение. Обратите внимание на то, что для вычисления пределов нужно использовать не знак равенства, который используется в численных вычислениях, а стрелочку — знак вывода результатов символьных преобразований, который записывается с помощью клавиатурной комбинации Ctrl+точка (русское «ю»).

С помощью пределов в MathCAD’е можно вычислять и производные. Если вы помните, то производная по определению равна пределу приращения функции к приращению аргумента этой функции при условии, что это приращение стремится к нулю. Выбрав любую функцию, вы можете легко вычислить ее производную с использованием пределов точно так же, как это показано для натурального логарифма на соответствующей иллюстрации к статье.

Впрочем, вычислять производные таким образом, мягко говоря, не очень удобно, а потому в MathCAD’е существуют специальные операторы, позволяющие вычислять производные функций. О том, как ими правильно воспользоваться, мы с вами сейчас и поговорим.

Вычисление производных

Вычислять полные производные выражений любой сложности в MathCAD’е так же просто, как вычислять пределы. Для этого на все той же панели Calculus присутствует специальная кнопка, при нажатии на которую появляется оператор вычисления производной, который, как и в матанализе, имеет запись d/dx. Вместо x, конечно, может стоять любая другая переменная. Выражение, для которого мы должны рассчитать производную, должно записываться после оператора ее вычисления. Как и в случае с пределом, для получения результата мы должны воспользоваться оператором аналитического вычисления значения производной.

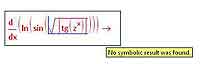
MathCAD умеет вычислять производные даже довольно сложных и громоздких выражений, хотя и не всегда выдает результаты подобных вычислений в удобной для пользователя форме. Тем не менее, если выражение будет очень сложным, то и MathCAD может с ним не справиться, что показывает соответствующая иллюстрация ниже.

Для получения численного значения производной в какой-то конкретной точке целесообразно использовать следующую схему: присвоить какой-либо новой функции значение производной от нужной вам функции, а после подставлять значение той точки, в которой нужно узнать производную, в эту новую функцию. Также, в принципе, можно воспользоваться изложенным выше методом вычисления производной с помощью пределов. Этот метод в общем случае является более корректным, поскольку MathCAD при попытке непосредственного вычисления производной функции в той точке, где она разрывается, может выдавать неверные результаты. Аналогичные результаты можно получить и при использовании оператора численного равенства (т.е. обычного знака «равно») при вычислении производной. Но тогда выше нужно будет указать значение переменной, для которого мы вычисляем производную численно.

Следует отметить, что вычисление производной аналитически, а затем подстановка конкретного значения переменной в функцию, выражающую производную данной функции, дает более точные результаты, чем непосредственное численное дифференцирование изначальной функции. Но, к сожалению, такой прим удается применить не всегда — как уже говорилось выше, встречаются ситуации, когда MathCAD’у не по силам вычислить аналитически значение производной функции. Тем не менее, точность численного вычисления значения производной в точке очень высока: не менее семи знаков после запятой являются верными, а в большинстве случаев она еще выше — от 10 до 12 знаков после запятой. Такой точности вполне хватает даже для очень точных расчетов, а потому использование в них численного дифференцирования вполне оправдано.

Для вычисления производных второго и более высокого порядков нужно использовать специальный оператор n-й производной функции, расположенный на панели Calculus рядом с оператором первой производной. Как и другие обозначения операторов в MathCAD’е, здесь используется общепринятое математическое обозначение dn/dxn.

В общем-то, вычисление производных высших порядков в MathCAD’е по своему принципу мало чем отличается от вычисления первой производной. Стоит заметить, впрочем, что с помощью MathCAD’а невозможно получить выражение для последующего вычисления производной n-го порядка путем подстановки числа n в какую-либо формулу. Дело в том, что оператор вычисления производных высших порядков допускает использование в качестве порядка производной только числовую константу (естественно, показатель должен быть натуральным числом). В общем-то, больше никаких особых ограничений оператор вычисления n-й производной на действия пользователя не накладывает.

Единственное, пожалуй, на что еще стоит обратить внимание при работе с производными высших порядков, это то, что численное дифференцирование с ними нужно производить куда аккуратнее, чем с первыми производными, так как существует проблема накопления погрешности при вычисления каждого следующего порядка производной через предыдущие. Уже для производных пятого порядка точность падает обычно до пяти знаков после запятой, а потому лучше использовать методы подстановки конкретных значений точек, в которых должна быть вычислена производная, в ее аналитическое выражение. Все же производные в большинстве случаев поддаются вычислению аналитически, а потому к численному дифференцированию для высоких порядков производной лучше вовсе не прибегать.

Вычисление производных, конечно же, не ограничивается этими двумя простыми случаями (полной производной первого и более высоких порядков), а потому в следующий раз мы немного поговорим о некоторых более сложных аспектах дифференцирования. Сейчас же мы перейдем к другому разделу математического анализа — рядам.

Ряды

Числовые и функциональные ряды играют очень важную роль в математическом анализе. Они позволяют переходить от непрерывного представления функции, используемого, например, в физике, к дискретному, которое необходимо для вычисления ее значения с помощью компьютера. Поэтому работа с рядами поддерживается MathCAD’ом в полной мере.

Самая важная операция, касающаяся как числовых, так и функциональных рядов — это, конечно же, вычисление суммы ряда. Найти оператор вычисления этой суммы без труда можно на все той же панели Calculus, и выглядит он, как и в математике, как большая греческая буква сигма. Для вычисления суммы ряда необходимо задать индекс суммирования (для определенности будем полагать, что он записывается буквой n), диапазон суммирования и, конечно же, значение n-го члена ряда. При этом можно использовать символ бесконечности для вычисления сумм бесконечных рядов (этот символ находится на все той же панели Calculus, сразу за оператором вычисления n-й производной). При этом стоит отметить, что вычисление суммы конечного ряда возможно как аналитически, так и численно, т.е. можно использовать и знак равенства, и стрелку, а вот для бесконечного ряда найти сумму можно только аналитическим путем.

Как и в других областях, где MathCAD задействует свой символьный процессор, всплывают на поверхность и начинают раздражать пользователя минусы этого самого символьного процессора. Самый главный из них, с которым мы с вами уже сталкивались — это нежелание полноценно работать с тригонометрическими функциями. Поэтому если вам нужно рассчитать сумму тригонометрического ряда, то на MathCAD в этом случае можете не рассчитывать.

Суммы функциональных рядов можно сразу дифференцировать и интегрировать (про интегрирование функций средствами MathCAD’а мы с вами поговорим позже), причем можно производить дифференцирование или интегрирование как всей суммы сразу, так и отдельных членов ряда. Пример того, как это можно сделать, показан на приведенной ниже иллюстрации. Правда, как вы видите, может показаться, будто бы результаты различаются, но если упростить первое выражение, то станет понятно, что на самом деле они абсолютно идентичны.

В общем, MathCAD действительно хороший помощник при работе с производными, пределами, рядами и, как мы с вами далее убедимся, интегралами. Конечно, невозможность работы с тригонометрическими рядами — это довольно серьезный минус, ведь тригонометрические ряды Фурье используются для разложения периодических функций, однако на самом деле, учитывая все плюса MathCAD’а, этот минус не так уж и велик. MathCAD’у вполне по силам упростить работу с производными и интегралами, а о том, как справиться с громоздкостью получаемых результатов средствами самой среды MathCAD, мы еще побеседуем.

SF, spaceflyer@tut.by