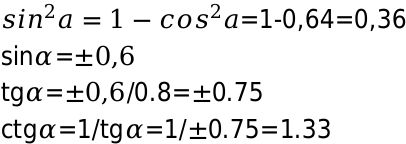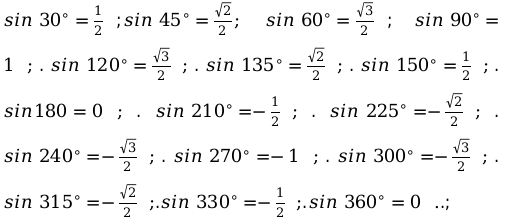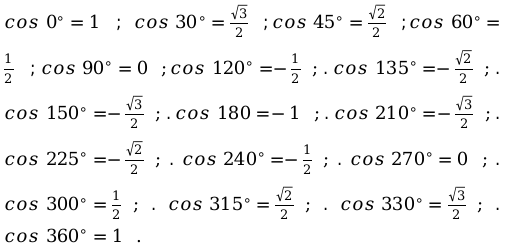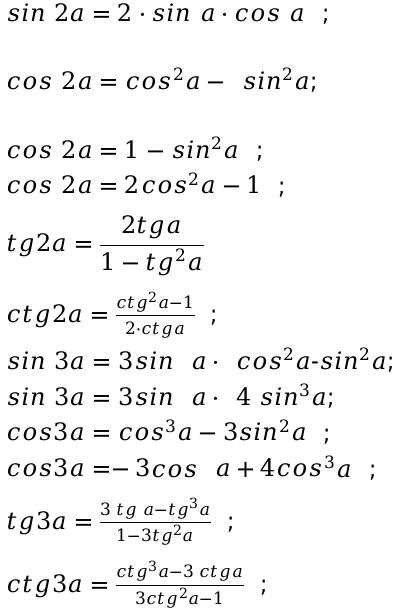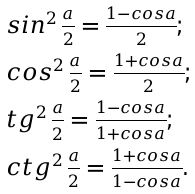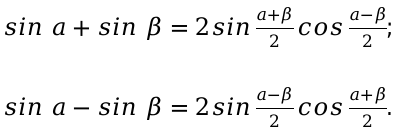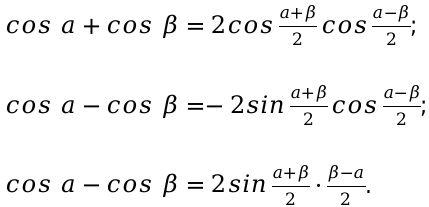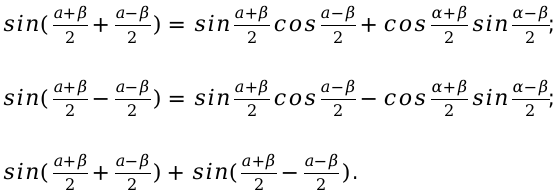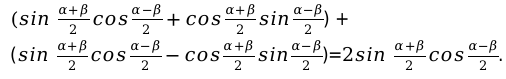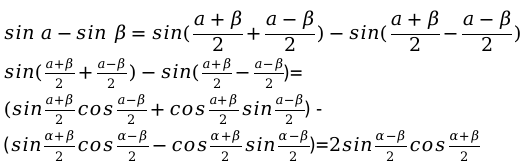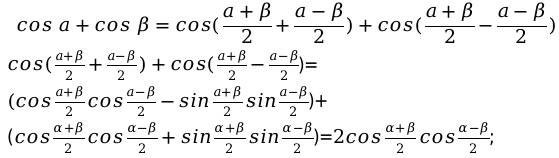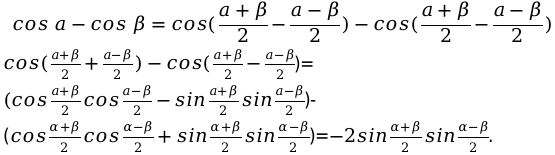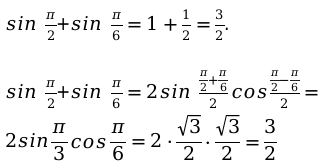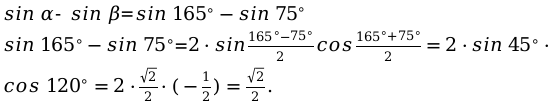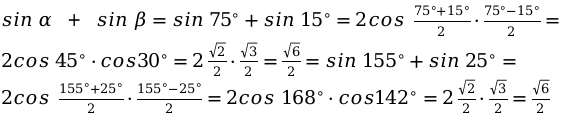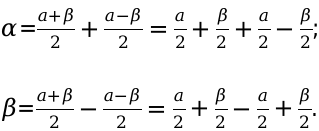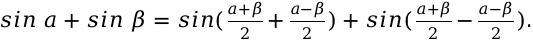Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
В математике применяются основные определения, связанные с тригонометрией. А именно:
- синус — соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
- косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos);
Стоит выделить главные тригонометрические тождества, существующие в математике:
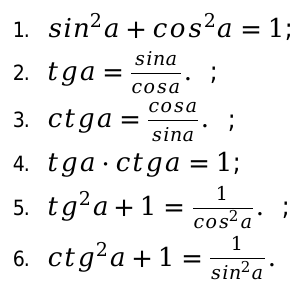
Применим основные формулы тригонометрии, решая задачи.
Пример:
Известно: [cos alpha=0.8];
Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.
Решение:
Для определения значения косинуса в квадрате, возводим число 0,8 в квадрат и вычисляем синус. Полученное значение подставляем в формулу и можем определить тангенс угла 0,8. Таким же методом, вычисляем котангенс
Решение довольно простое и особых сложней не вызывает.
Основные формулы для приведения заданных значений:
Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.
Существует два основных способа, использования формул приведения:
- Если угол можно записать как [(pi / 2 pm alpha)] или [left(3^{*} pi / 2 pm alpharight)], то название функции меняется с косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде [(pi pm alpha)] или [(2 * pi pm alpha)], то название функции не меняется.
- Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.
Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.
Значения функций тригонометрии на для основных угловых значений.
- синуса (sin):
- косинуса (cos):
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.
Формулы кратности значения угла:
Формулы угла, определяющие половину значения (половинного угла):
Более подробно в данном материале мы рассмотрим все уравнения суммы и разности, связанные именно с функцией косинус и синус.
Основные формулы для определения суммы и разности cos и sin
Перейдем к рассмотрению к простой форме разности и суммы функций.
Рассматриваемое уравнений можно представить, как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.
Составим и запишем основные формулы для функции синус.
Следующим основным шагом, будет составить уравнения для косинуса. Применим все изученные свойства данной функции тригонометрии и вычислим правильный ответ.
Выведем основные формулы для решения функций двух угловых значений. Для этого нужно применить составленные выше формулы сложения и вычитания. Их рассмотрение было в предыдущих материалах, посвященных тригонометрии. Поэтому лишний раз не стоит их заново переписывать. Так как рекомендовалась их обязательно заучить наизусть. Для более быстрого и правильного решения уравнений. И для последующего использования при изучении других смежных тем, где эти функции применяются.
Формулы можно представить также в виде полусуммы и полуразности угловых значений и получить следующие формулы.
Запишем уравнение для каждого угла раздельно и получим следующие формулы в виде уравнения:
[
alpha=frac{a+beta}{2}+frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}+frac{a}{2}-frac{beta}{2}
]
[
beta=frac{a+beta}{2}-frac{a-beta}{2}=frac{a}{2}+frac{beta}{2}-frac{a}{2}+frac{beta}{2}
]
Сравним записанные формулы для угловых значений. Проанализировав их становится очевидно, что полученные суммы функций одинаковы по значению.
Выведем основную формулу для решения:
[
sin a+sin beta=sin left(frac{a+beta}{2}+frac{a-beta}{2}right)+sin left(frac{a+beta}{2}-frac{a-beta}{2}right) .
]
Далее первую часть выражения преобразуем, для этого применим формулу для сложения функций. Значения, которые находятся после знака равно, преобразуются при помощи формулы синуса для разности.
Подставляя в формулу значения, получаем следующее выражение:
Далее необходимо раскрыть скобки и полученные значения привести в подобные слагаемые. Произведя все действия мы в конечном итоге получаем нужную нам формулу.
Запишем формулу следующего вида:
Другие, формулы преобразуются аналогичным способом
Нет времени решать самому?
Наши эксперты помогут!
Итоговые формулы сложения и вычитания тригонометрических функций
Формула определения разности для синуса:
Формула для расчета суммы косинуса:
Рассмотрим на практике применение изученного материала. Для этого решим несколько задач, подставляя числовые угловые значения
Пример №1:
По заданию нужно проверить сумму угловых значений для изученной функции подставив данные в формулу.
Заданы значения: [alpha=frac{pi}{2} ; beta=frac{pi}{6}].
Подберем нужную формулу и произведем вычисление:
Пример №2:
В этом примере рассмотрим вариант решения и применения формулы, для разности функции синуса.
Заданы следующие значения.
Углы: [alpha=165^{circ}, beta=75^{circ}]
Подставим угловые значения в формулу:
Пример №3:
Нужно найти сумму тригонометрической функции.
Для этого заданы угловые значения.
Применяя основные изученные формулы, решим данную задачу.
Применяя вышеизложенные формулы можно перейти к произведению функций.
В целом, данная тема, считается основой в алгебре. Однако стоит вспомнить, что данные функции имеют главную роль и в других технических науках.
Они встречаются во многих теоремах, особенно это свойственно для физики.
Для всех технических наук, характерна взаимосвязь между основными законами и теоремами. Поэтому для успешного решения задач разного уровня, необходимо изучать и уметь их всех применять на практике.
Ниже в табличном виде представлены формулы сумм основных тригонометрических функций.
Содержание
- Прямые и производные функции: sin, cos, tg, ctg
- Обратные функции: arcsin, arccos, arctg, arcctg
Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
| Действие | Формула |
| Сумма синусов |  |
| Сумма косинусов |  |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β |
| Сумма котангенсов | ctg α + ctg β = sin (α + β) / sin α sin β |
microexcel.ru
Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
| Действие | Формула |
| Сумма арксинусов |
 |
| Сумма арккосинусов |
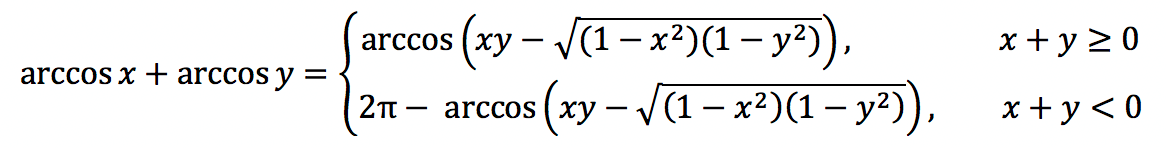 |
| Сумма арктангенсов |
 |
| Сумма арккотангенсов |
 |
microexcel.ru
Сумма и разность синусов и косинусов: вывод формул, примеры
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin ( α + β ) = sin α · cos β + cos α · sin β sin ( α — β ) = sin α · cos β — cos α · sin β cos ( α + β ) = cos α · cos β — sin α · sin β cos ( α — β ) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Сумма и разность синусов и косинусов
Время чтения: 16 минут
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
В математике применяются основные определения, связанные с тригонометрией. А именно:
- синус — соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
- косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos);
Стоит выделить главные тригонометрические тождества, существующие в математике:
Применим основные формулы тригонометрии, решая задачи.
Пример:
Известно: 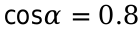
Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.
Для определения значения косинуса в квадрате, возводим число 0,8 в квадрат и вычисляем синус. Полученное значение подставляем в формулу и можем определить тангенс угла 0,8. Таким же методом, вычисляем котангенс
Решение довольно простое и особых сложней не вызывает.
Основные формулы для приведения заданных значений:
Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.
Существует два основных способа, использования формул приведения:
- Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.
Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.
Значения функций тригонометрии на для основных угловых значений.
- синуса (sin):
- косинуса (cos):
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.
Формулы кратности значения угла:
Формулы угла, определяющие половину значения (половинного угла):
Более подробно в данном материале мы рассмотрим все уравнения суммы и разности, связанные именно с функцией косинус и синус.
Основные формулы для определения суммы и разности cos и sin
Перейдем к рассмотрению к простой форме разности и суммы функций.
Рассматриваемое уравнений можно представить, как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.
Составим и запишем основные формулы для функции синус.
Следующим основным шагом, будет составить уравнения для косинуса. Применим все изученные свойства данной функции тригонометрии и вычислим правильный ответ.
Выведем основные формулы для решения функций двух угловых значений. Для этого нужно применить составленные выше формулы сложения и вычитания. Их рассмотрение было в предыдущих материалах, посвященных тригонометрии. Поэтому лишний раз не стоит их заново переписывать. Так как рекомендовалась их обязательно заучить наизусть. Для более быстрого и правильного решения уравнений. И для последующего использования при изучении других смежных тем, где эти функции применяются.
Формулы можно представить также в виде полусуммы и полуразности угловых значений и получить следующие формулы.
Запишем уравнение для каждого угла раздельно и получим следующие формулы в виде уравнения:
Сравним записанные формулы для угловых значений. Проанализировав их становится очевидно, что полученные суммы функций одинаковы по значению.
Выведем основную формулу для решения:
Далее первую часть выражения преобразуем, для этого применим формулу для сложения функций. Значения, которые находятся после знака равно, преобразуются при помощи формулы синуса для разности.
Подставляя в формулу значения, получаем следующее выражение:
Далее необходимо раскрыть скобки и полученные значения привести в подобные слагаемые. Произведя все действия мы в конечном итоге получаем нужную нам формулу.
Запишем формулу следующего вида:
Другие, формулы преобразуются аналогичным способом
http://skysmart.ru/articles/mathematic/teorema-sinusov
http://www.napishem.ru/spravochnik/matematika/summa-i-raznost-sinusov-i-kosinusov.html
$begingroup$
I wonder if there is a way to calculate the
$$S_n=sin x + sin 2x + … + sin nx$$
but using only derivatives ?
Aaron Maroja
17.3k5 gold badges26 silver badges56 bronze badges
asked Mar 2, 2015 at 20:34
$endgroup$
1
$begingroup$
Using telescopic sums:
$$ sin(mx)sin(x/2) = frac{1}{2}left(cosleft((m-1/2)xright)-cosleft((m+1/2)xright)right)$$
Hence:
$$ S_n sinfrac{x}{2} = frac{1}{2}left(cosfrac{x}{2}-cosleft(left(n+frac{1}{2}right)xright)right)=sinfrac{nx}{2}cdotsinfrac{(n+1)x}{2}.$$
abnry
14.4k2 gold badges34 silver badges75 bronze badges
answered Mar 2, 2015 at 20:40
Jack D’AurizioJack D’Aurizio
349k41 gold badges374 silver badges814 bronze badges
$endgroup$
5
$begingroup$
You may write
$$
begin{align}
sum_{k=1}^{n} sin (ktheta)&=Im sum_{k=1}^{n} e^{iktheta}\\
&=Imleft( e^{itheta}frac{e^{intheta}-1}{e^{itheta}-1}right)\\
&=Imleft( e^{itheta}frac{e^{intheta/2}left(e^{intheta/2}-e^{-intheta/2}right)}{e^{itheta/2}left(e^{itheta/2}-e^{-itheta/2}right)}right)\\
&=Imleft( e^{itheta}frac{e^{intheta/2}left(2isin(ntheta/2)right)}{e^{itheta/2}left(2isin(theta/2)right)}right)\\
&=Imleft( e^{i(n+1)theta/2}frac{sin(ntheta/2)}{sin(theta/2)}right)\\
&=Imleft( left(cos ((n+1)theta/2)+isin ((n+1)theta/2)right)frac{sin(ntheta/2)}{sin(theta/2)}right)\\
&=frac{sin ((n+1)theta/2)}{sin(theta/2)}sin(ntheta/2).
end{align}
$$
answered Mar 2, 2015 at 20:37
Olivier OloaOlivier Oloa
120k19 gold badges199 silver badges318 bronze badges
$endgroup$
2
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Синус суммы углов, формула
Данная формула позволяет найти синус суммы углов зная синус и косинус этих углов по отдельности:
[
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
]
Вычислить, найти синус суммы углов, по формуле (1)
| α° (градусов) | α´ (минут) | α˝ (секунд) |
| β° (градусов) | β´ (минут) | β˝ (секунд) |
Вычислить
нажмите кнопку для расчета
Синус суммы углов |
стр. 213 |
|---|