Как найти сумму собственных чисел матрицы - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Примеры с решением

Проблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах математики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции).

Пусть задана квадратная матрица размера , элементами которой являются действительные числа и вектор неизвестных размера :

Предположим, что — это некоторое неизвестное действительное число.

Если и ненулевой вектор удовлетворяют уравнению

то называется собственным числом или собственным значением матрицы , а — собственным вектором этой же матрицы, соответствующим .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Преобразуем уравнение (2.15) к следующему виду:

где — единичная матрица.

Матрица называется характеристической матрицей.

Так как по условию вектор неизвестных не равен нулю, то среди его координат должна быть хотя бы одна ненулевая.

А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли).

Поэтому получаем

Число, где будет собственным числом только в том случае, если матрица — вырожденная.

Уравнение (2.17) называется характеристическим уравнением матрицы и представляет собой алгебраическое уравнение степени относительно :

Уравнение (2.18) имеет корней . Множество всех корней уравнения (2.18) называется спектром матрицы .

Заметим, что уравнение имеет те же корни, что и уравнение (2.17), т. е.

Каждому собственному значению спектра матрицы ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя. Если есть кратный корень характеристического уравнения, то для произвольной квадратной матрицы число соответствующих собственных векторов может быть не равно кратности корня.

Возможно вам будут полезны данные страницы:

С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменяется и вдоль которого пространство испытывает растяжение или сжатие в раз.

Полином называют характеристическим полиномом. Коэффициенты можно вычислить по следующим рекуррентным формулам [57]:

Здесь — след матрицы (сумма элементов, стоящих на главной диагонали матрицы ). Заметим, что . При отыскании собственных чисел даже для матриц невысокого порядка неизбежно большое количество вычислений.

Для общего случая нельзя предложить оптимальный способ нахождения собственных чисел и собственных векторов матрицы.

Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диагональная, либо верхняя или нижняя треугольная). В этом случае собственные числа совпадают с элементами главной диагонали исходной матрицы

Пусть задана верхняя треугольная матрица размера Тогда имеем Отсюда видно, что собственные числа равны:

С появлением ЭВМ получили распространение итерационные методы нахождения собственных чисел, которые не используют вычисление характеристического полинома.

К этим способам относятся: степенной метод, метод обратных итераций, QR-алгоритм, метод вращений Якоби, QL-алгоритм и др.

Причем применение конкретного итерационного метода зависит от вида исходной матрицы А [4].

Теперь рассмотрим конкретные примеры.

Примеры с решением

Пример 2.8.

Дана матрица А размера (3 X 3)

Найти собственные числа и собственные векторы матрицы А.

Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали

Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем уравнение (2.16). Для получаем

где Далее раскроем матричное уравнение (2.20)

В результате получим

Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид:

т. е. получены искомые собственные вектора для Для получаем

или в подробной записи

В результате получаем

т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для Эти решения запишем в виде

Пример 2.9.

Дана матрица А размера (2 X 2). Найти собственные числа и собственные матрицы А

Запишем характеристическое уравнение (2.17) для данного случая

Теперь найдем собственные векторы исходной матрицы А, соответствующие и . Для имеем

В подробной записи получим Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собственными векторами , которые мы и находим

Из первого уравнения системы получаем Из второго уравнения системы получаем т. е. она имеет бесконечное множество решений. И искомый собственный вектор будет иметь вид

Аналогично, для находим

В заключение приведем два полезных правила [38]:

1) сумма собственных чисел матрицы А равна следу этой матрицы, т. е.

2) произведение собственных чисел матрицы А равно определителю этой матрицы

Кратко рассмотрим квадратичные формы. Квадратичной дборжой называется однородный многочлен второй степени от нескольких пременных. Обозначим их

Квадратичную форму в общем виде можно записать так:

В качестве примера рассмотрим квадратичную форму трех переменных:

Введем обозначения:

Тогда квадратичная форма примет вид

Дополнительно вводим симметричную матрицу В, вектор .

В этом случае квадратичная форма примет вид

Последняя формула представляет собой матрично-векторный вид квадратичной формы. А в общем случае получим:

где — коэффициенты при для всех , а равны полусуммам коэффициентов при элементах, содержащих произведения и при всех .

Матрица В является матрицей квадратичной формы. В качестве примера запишем в матрично-векторном виде квадратичную форму

В данном случае получаем:

Матрица данной квадратичной формы принимает вид

А ее матрично-векторная запись такова:

Лекции:

Системы линейных дифференциальных уравнений
Свойства пределов функции
Решение пределов со степенями
Теория сплайнов примеры решения
Жорданова форма матрицы
Исследование графика функции
Существование предела
Приложения двойных и тройных интегралов
Производная функции
Найдите наименьшее значение функции на отрезке

Источник

Элементарные преобразования.

отбрасывание
нулевой строки (столбца);
умножение
всех элементов строки (столбца) матрицы
на число, не равное нулю;
изменение
порядка строк (столбцов) матрицы;
прибавление
к каждому элементу одной строки (столбца)
соответствующих элементов другой
строки (столбца), умноженных на любое
число;
транспонирование
матрицы.

С помощью элементарных
преобразований можно привести матрицу
к так называемому ступенчатому виду,
тогда вычисление ранга не представляет
труда.

Матрица А
называется ступенчатой,
если она имеет вид:

,
где

i=1,2,…,r;
r
k.

Замечание:
условие r
k
всегда может быть достигнуто
транспонированием матрицы.

Очевидно, что ранг
ступенчатой матрицы равен r,
так как имеется минор r-го
порядка, не равный нулю:

Покажем на примере
алгоритм
вычисления ранга матрицы
с помощью элементарных преобразований.

Пример 9 :
Найти ранг матрицы

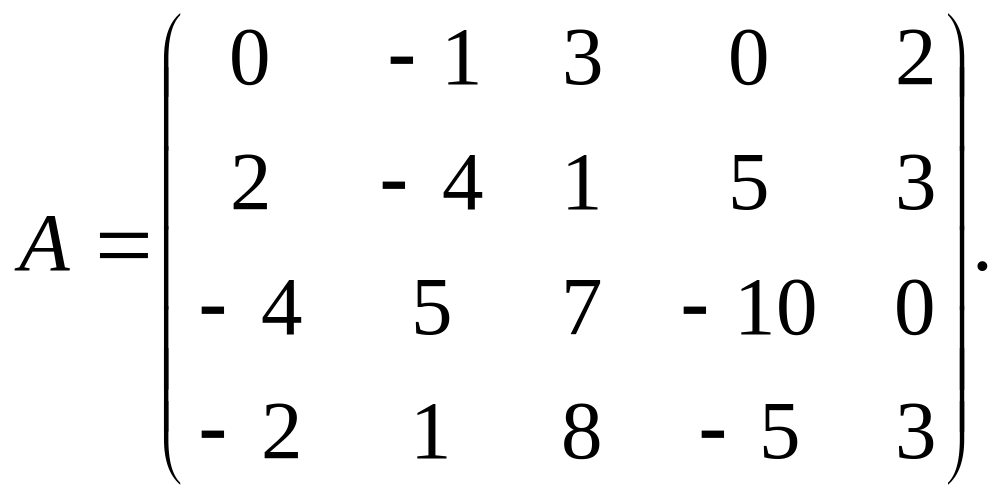
Если

,
то при перестановке строк или столбцов
добиваемся того, что

.
В данном случае поменяем местами,
например 1-ю и 2-ю строки матрицы.
Если

,
то умножая элементы 2-й, 3-й, 4-й строк но
подходящие числа (именно на

,

)
и прибавляя полученные числа соответственно
к элементам 2-й, 3-й, и 4-й строк, добьёмся
того, чтобы все элементы первого столбца
(кроме

)
равнялись нулю:

Если
в полученной матрице

(в нашем случае

),
то умножая элементы 3-й и 4-й строк на
подходящие числа (а именно, на

),
добьёмся того, чтобы все элементы 2-го
столбца (кроме

,

)
равнялись нулю. Если в процессе
преобразований получаются строки (или
столбцы), целиком состоящие из нулей
(как в данном примере), то отбрасываем
эти строки (или столбцы):

Последняя матрица
имеет ступенчатый вид и содержит миноры
второго порядка, не равные нулю, например,

Поэтому ранг полученной ступенчатой
матрицы, а следовательно, и данной
матрицы равен 2.

Для рангов матриц
справедливы следующие соотношения:

r(A+B)
r(A)+r(B);
r(A+B)

;
r(AB)
;
r(A
A)=r(A);
r(AB)=r(A),
если А и В – квадратные матрицы и

.

Собственные числа. Собственные векторы матрицы.

Пусть
дана матрица

,
и

—n-мерный
вектор.

Число

,
удовлетворяющее уравнению

(1), называется собственным
числом (значением)
матрицы А.

Ненулевой вектор

,
соответствующий числу

уравнения (1), называется собственным
вектором
матрицы А.

Множество собственных
чисел матрицы А,
называется её спектром.
Иногда собственные числа матрицы,
называют её характеристическими
корнями,
а собственные векторы – характеристическими
векторами.

Уравнение (1) можно
записать в виде

(2), где

— n—
мерный нуль-вектор.

Матрица А
имеет собственный вектор

,
если матрица

вырожденная, то есть её определитель
равен нулю:

.
(3)

Равенство (3)
является уравнением n-степени
относительно переменной

Уравнение (3)
называется характеристическим
уравнением
матрицы А,
определитель

— её характеристическим
многочленом.

Итак,
чтобы найти собственные числа матрицы,
надо составить и решить её характеристическое
уравнение.

Чтобы найти
собственный вектор, соответствующий
собственному числу

,
надо решить матричное уравнение (2), то
есть систему однородных линейных
уравнений, матрица которой – вырожденная.

Пример 10:
Найти собственные числа и собственные
векторы матрицы

.

Решение.

Составим и решим
характеристическое уравнение

Итак, матрица А
имеет два действительных собственных
числа (-2) и 13.

Собственные векторы
матрицы А,
соответствующие собственному числу

,
находим решая систему

эта система
равносильна одному уравнению

Пусть

,
тогда

Получим, что собственные векторы матрицы
А,
соответствующие собственному числу

имеет вид

,
где к
– любое число, не равное нулю.

Найдем собственные
векторы матрицы А,
соответствующие собственному числу

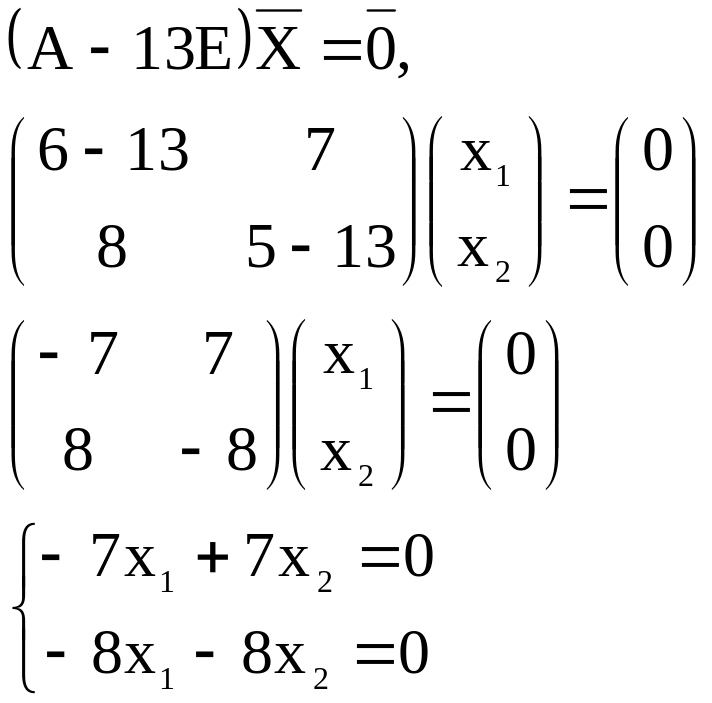
Эта система
равносильна одному уравнению

.

Собственные векторы
матрицы А,
соответствующие собственному числу

имеют вид
,
где к
– любое, не равное нулю, число.

В экономических
приложениях полезно использовать
некоторые свойства собственных чисел
и собственных векторов матрицы.

Свойства
собственных чисел матрицы.

Сумма диагональных
элементов матрицы называется её следом
и записывается
TrA.

Сумма
собственных чисел матрицы А
равна следу этой матрицы.

Пример
11: Для
матрицы

TrA=6+5=11
и, действительно,

.

Произведение
собственных чисел матрицы А
равно определителю этой матрицы.

Пример
12:

Число
отличных от нуля собственных чисел
матрицы А
равно её рангу.

Пример
13: rA=2,
и число собственных чисел отличных от
нуля тоже равно 2.

Все
собственные числа матрицы А
отличны от нуля, в том и только в том
случае, если матрица А
невырожденная.
Если

₀
– собственное число невырожденной
матрицы А,
то

— собственное число матрицы А^—¹.
Если

₀
– собственное число матрицы А,
то

₀^к—
собственное число матрицы А^к
при любом целом к
1.
Собственными
числами диагональной матрицы являются
числа, стоящие на её главной диагонали.

Рекомендуется
проверить самостоятельно.

Свойства
собственных векторов матрицы.

Собственные
векторы матрицы, соответствующие её
различным собственным числам, линейно
– независимы.
Если
все собственные числа квадратной
матрицы n-го
порядка различны, то соответствующие
им собственные векторы образуют базис
пространства Rⁿ.
Любая,
не равная нулевому вектору линейная
комбинация собственных векторов данной
матрицы, соответствующих одному и тому
же собственному числу этой матрицы,
также является собственным вектором
данной матрицы.

Рассмотрим
использование в экономике собственных
чисел и собственных векторов квадратной
матрицы на примере линейных моделей
обмена.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Собственные векторы и собственные значения матрицы

Пусть — числовая квадратная матрица n-го порядка. Матрица A-lambda E называется характеристической для , а ее определитель $Delta_{A}(lambda)=det(A-lambda E)$ характеристическим многочленом матрицы

$A-lambda E=begin{pmatrix}a_{11}-lambda&cdots&a_{1n}\ vdots&ddots& vdots\ a_{n1}&cdots&a_{nn}-lambdaend{pmatrix}!,quad Delta_{A}(lambda)=det(A-lambda E)= begin{vmatrix} a_{11}-lambda&cdots&a_{1n}\ vdots&ddots&vdots\ a_{n1}&cdots&a_{nn}-lambdaend{vmatrix}!.$

(7.12)

Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.

Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец $x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}$ , удовлетворяющий условию

Acdot x=lambdacdot x,

(7.13)

называется собственным вектором матрицы . Число lambda в равенстве (7.13) называется собственным значением матрицы . Говорят, что собственный вектор соответствует {принадлежит) собственному значению lambda .

Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде (A-lambda E)x=o , где — единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему линейных алгебраических уравнений с неизвестными x_1,x_2,ldots,x_n:

$begin{cases}(a_{11}-lambda)x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+(a_{22}-lambda)x_2+ldots+a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{n1}x_1+a_{2n}x_2+ldots+(a_{nn}-lambda)x_n=0. end{cases}$

(7.14)

Поскольку нас интересуют только нетривиальные решения (xne o) однородной системы, то определитель матрицы системы должен быть равен нулю:

$det(A-lambda E)=begin{vmatrix}a_{11}-lambda&a_{12}&cdots&a_{1n}\ a_{21}&a_{22}-lambda&cdots&a_{2n}\ vdots&vdots&ddots&vdots\ a_{n1}&a_{n2}& cdots&a_{nn}-lambda end{vmatrix}=0.$

(7.15)

В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена $Delta_{A}(lambda)=det(A-lambda E)$ матрицы . Уравнение $Delta_{A}(lambda)=0$ называется характеристическим уравнением матрицы . Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде

$Delta_{A}(lambda)= det(A-lambda E)= a_{n}(lambda-lambda_1)^{n_1}cdot (lambda-lambda_2)^{n_2}cdotldotscdot(lambda-lambda_k)^{n_k},$

где lambda_1,lambda_2,ldots,lambda_k — корни многочлена кратности n_1,n_2,ldots,n_k соответственно, причем n_1+n_2+ldots+n_k=n . Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.

Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.

Действительно, если число lambda — собственное значение матрицы , которому соответствует собственный вектор xne o , то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число lambda удовлетворяет характеристическому уравнению (7.15). Наоборот, если lambda — корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е. operatorname{rg}(A-lambda E)<n .В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец xne o , удовлетворяющий условию (7.14). Значит, lambda — собственное значение матрицы .

Свойства собственных векторов

Пусть — квадратная матрица n-го порядка.

1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.

В самом деле, пусть s_1 и s_2 — собственные векторы, соответствующие собственным значениям lambda_1 и lambda_2 , причем lambda_1ne lambda_2 . Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:

alpha_1cdot s_1+alpha_2cdot s_2=o.

(7.16)

Надо показать, что это равенство возможно только в тривиальном случае, когда alpha_1=alpha_2=0 . Действительно, умножая обе части на матрицу и подставляя As_1=lambda_1s_1 и As_2=lambda_2s_2 имеем

A(alpha_1s_1+alpha_2s_2)=oquad Leftrightarrowquad alpha_1As_1+ alpha_2As_2= oquad Leftrightarrowquad alpha_1 lambda_1s_1+alpha_2 lambda_2s_2=o.

Прибавляя к последнему равенству равенство (7.16), умноженное на (-lambda_2) , получаем

alpha_1cdotlambda_1cdot s_1-alpha_2cdotlambda_2cdot s_2=oquad Leftrightarrowquad alpha_1cdot(lambda_1-lambda_2)cdot s_1=o.

Так как s_1ne o и lambda_1ne lambda_2 , делаем вывод, что alpha_1=0 . Тогда из (7.16) следует, что и alpha_2=0 (поскольку s_2ne o ). Таким образом, собственные векторы s_1 и s_2 линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.

2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.

Действительно, если собственному значению lambda соответствуют собственные векторы s_1,ldots,s_k , то из равенств S_i=lambda s_i, i=1,ldots,k , следует, что вектор s=alpha_1s_1+ldots+alpha_ks_k также собственный, поскольку:

As=A(alpha_1s_1+ldots+alpha_ks_k)= alpha_1lambda s_1+ldots+alpha_klambda s_k=lambda(alpha_1s_1+ldots+alpha_ks_k)=lambda s.

3. Пусть $(A-lambda E)^{+}$ — присоединенная матрица для характеристической матрицы . Если lambda_0 — собственное значение матрицы , то любой ненулевой столбец матрицы $(A-lambda E)^{+}$ является собственным вектором, соответствующим собственному значению .

В самом деле, применяя формулу (7.7) имеем $(A-lambda E)(A-lambda E)^{+}=Delta_k(lambda)cdot E$ . Подставляя корень lambda_0 , получаем $(A-lambda_0E)(A-lambda_0E)^{+}=O$ . Если — ненулевой столбец матрицы $(A-lambda_0E)^{+}$ , то (A-lambda_0E)s=oLeftrightarrow As=lambda_0s . Значит, — собственный вектор матрицы .

Замечания 7.5

1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.

2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений lambda_1,lambda_2, ldots,lambda_k записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем

(A-lambda_1E)cdot x=o,quad (A-lambda_2E)cdot x=o,quad ldots,quad (A-lambda_kE)cdot x=o.

Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.

3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.

4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).

5. Для простого корня lambda=lambda_0 характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы (A-lambda_0E) по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы , является собственным вектором.

Нахождение собственных векторов и собственных значений матрицы

Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.

1. Составить характеристический многочлен матрицы Delta_A(lambda)=det(A-lambda E) .

2. Найти все различные корни lambda_1,lambda_2,ldots,lambda_k характеристического уравнения Delta_A(lambda)=0 (кратности n_1,n_2,ldots,n_k (n_1+n_2+ldots+n_k=n) корней определять не нужно).

3. Для корня lambda-lambda_1 найти фундаментальную систему $varphi_1,varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений

(A-lambda_1E)cdot x=o , где $r=operatorname{rg}(A-lambda_1E)$

Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).

4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению lambda_1:

$s_1=C_1varphi_1,quad s_2=C_2varphi_2,quad ldots,quad s_{n-r}=C_{n-r}varphi_{n-r},$

(7.17)

где $C_1,C_2,ldots,C_{n-r}$ — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению lambda_1 , образуют ненулевые столбцы вида $s=C_1varphi_1+C_2varphi_2+ldots+C_{n-r}varphi_{n-r}$ . Здесь и далее собственные векторы матрицы будем обозначать буквой .

Повторить пункты 3,4 для остальных собственных значений lambda_1,lambda_2,ldots,lambda_k .

Пример 7.8. Найти собственные значения и собственные векторы матриц:

$A=begin{pmatrix}1&-2\3&8end{pmatrix}!,quad B=begin{pmatrix}1&-4\ 1&1 end{pmatrix}!,quad C=begin{pmatrix}1&1&1\1&1&1\1&1&1end{pmatrix}!.$

Решение. Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{A}(lambda)=begin{vmatrix}1-lambda&-2\3&8-lambdaend{vmatrix}= (1-lambda)(8-lambda)+6=lambda^2-9 lambda+8+6= lambda^2-9 lambda+14.$

2. Решаем характеристическое уравнение: $lambda^2-9 lambda+14=0~Rightarrow~! left[!begin{gathered}lambda_1=2,\ lambda_2=7.end{gathered}right.$ .

3(1). Для корня lambda_1=2 составляем однородную систему уравнений (A-lambda_1E)x=o:

$begin{pmatrix}1-2&-2\ 3&8-2 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-1&-2\ 3&6 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-1&-2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}-2\1end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1=2colon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы $begin{pmatrix}-1&-2\3&6end{pmatrix}$ , то есть $begin{pmatrix}2\-1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=7 составляем однородную систему уравнений (A-lambda_2E)x=o:

$begin{pmatrix}1-7&-2\ 3&8-7 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-6&-2\ 3&1 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-6&-2!!&vline!!&0\ 3&1!!&vline!!&0end{pmatrix}sim begin{pmatrix}3&1!!&vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: $x_1=-frac{1}{3}x_2$ . Полагая x_2=1 , получаем решение $varphi_2=begin{pmatrix}-1/3\1end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=7colon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-6&-2\3&1end{pmatrix}$ , т.е. $begin{pmatrix}1\-3 end{pmatrix}$ . Поделив его на (- 3), получим varphi_2 .

Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{B}(lambda)= begin{vmatrix}1-lambda&-4\1&1-lambdaend{vmatrix}= (1-lambda)^2+4=lambda^2-2 lambda+1+4= lambda^2-2 lambda+5.$

2. Решаем характеристическое уравнение: $lambda^2-2 lambda+5=0~Rightarrow~! left[! begin{gathered}lambda_1=1+2i,\ lambda_2=1-2i.end{gathered}right.$ .

3(1). Для корня lambda_1=1+2i составляем однородную систему уравнений (B-lambda_1E)x=o

$begin{pmatrix}1-(1+2i)&-4\ 1&8-1-(1+2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-2i&-4\ 1&-2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-2i&-4!!&vline!!&0\ 1&-2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&-2i!!&vline!!&0\ -2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&-2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=2i,x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}2i\1 end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1= 1+2icolon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2i&-4\1&-2iend{pmatrix}$ , то есть $begin{pmatrix}-2i\ -1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=1-2i составляем однородную систему уравнений (B-lambda_2E)x=o:

$begin{pmatrix}1-(1-2i)&-4\ 1&8-1-(1-2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}2i&-4\ 1&2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}2i&-4!!&vline!!&0\ 1&2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&2i!!&vline!!&0\ 2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2i,x_2 . Полагая x_2=1 , получаем решение $varphi_2= begin{pmatrix}-2i\1 end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=1-2icolon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}2i&-4\1&2iend{pmatrix}$ , т.е. $begin{pmatrix}2i\-1 end{pmatrix}$ . Умножив его на (-1), получим varphi_2 .

Матрица 1. Составляем характеристический многочлен матрицы

$Delta_{C}(lambda)= det(C-lambda E)= begin{vmatrix}1-lambda&1&1\1&1-lambda&1\ 1&1&1-lambda end{vmatrix}= (1-lambda)^3+2-3(1-lambda)= -lambda^3+3 lambda^2.$

2. Решаем характеристическое уравнение: $-lambda^3+3 lambda^2=0~Rightarrow~! left[! begin{gathered}lambda_1=3,\ lambda_2=0end{gathered}right.$ .

3(1). Для корня lambda_1=3 составляем однородную систему уравнений (C-lambda_1E)x=o:

$begin{pmatrix}1-3&1&1\ 1&1-3&1\ 1&1&1-3end{pmatrix}!cdot! begin{pmatrix} x_1\x_2\x_3end{pmatrix}=begin{pmatrix}0\0\0end{pmatrix}quad Leftrightarrowquad begin{cases}-2x_1+x_2+x_3=0,\ x_1-2x_2+x_3=0,\ x_1+x_2-2x_3=0.end{cases}$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):

$begin{gathered}begin{pmatrix}C-lambda_1Emid oend{pmatrix}= begin{pmatrix} -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0\ 1&1&-2!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0 end{pmatrix}sim\[2pt] simbegin{pmatrix} 1&1&-2!!&vline!!&0\ 0&3&-3!!&vline!!&0\ 0&-3&3!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&0&-1!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.end{gathered}$

Ранг матрицы системы равен 2 (r=2) , число неизвестных n=3 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисные переменные x_1,x_2 через свободную $x_3colon begin{cases}x_1=x_3,\x_2=x_3,end{cases}$ и, полагая x_3=1 , получаем решение $varphi=begin{pmatrix}1\1\1end{pmatrix}$ .

4(1). Все собственные векторы, соответствующие собственному значению lambda_1=3 , вычисляются по формуле s=C_1cdotvarphi , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2&1&1\1&-2&1\1&1&-2end{pmatrix}$ , то есть $begin{pmatrix}3\3\3end{pmatrix}$ , так как

$A_{11}=(-1)^{1+1}begin{vmatrix} -2&1\1&-2 end{vmatrix} =3;quad A_{12}=(-1)^{1+2} begin{vmatrix} 1&1\1&-2 end{vmatrix}= 3;quad A_{13}=(-1)^{1+3}begin{vmatrix}1&-2\ 1&1 end{vmatrix}=3.$

Разделив его на 3, получим varphi .

3(2). Для собственного значения lambda_2=0 имеем однородную систему Cx=o . Решаем ее методом Гаусса:

$begin{pmatrix}Cmid oend{pmatrix}= begin{pmatrix}1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0 end{pmatrix}sim begin{pmatrix}1&1&1!!& vline!!&0\ 0&0&0!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.$

Ранг матрицы системы равен единице (r=1) , следовательно, фундаментальная система решений состоит из двух решений (n-r=2) . Базисную переменную x_1 , выражаем через свободные: x_1=-x_2-x_3 . Задавая стандартные наборы свободных переменных x_2=1,~x_3=0 и x_2=0,~ x_3=1 , получаем два решения

$varphi_1=begin{pmatrix}-1\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-1\0\1 end{pmatrix}!.$

4(2). Записываем множество собственных векторов, соответствующих собственному значению lambda_2=0colon~ s=C_1varphi_1+C_2varphi_2 , где C_1,C_2 — произвольные постоянные, не равные нулю одновременно. В частности, при C_1=0, C_2=-1 получаем $s_1=begin{pmatrix}1&0&-1end{pmatrix}^T$ ; при C_1=0,~C_2=-1colon $s_2=begin{pmatrix}1&-1&0end{pmatrix}^T$ . Присоединяя к этим собственным векторам собственный вектор $s_3=begin{pmatrix}1&1&1 end{pmatrix}^T$ , соответствующий собственному значению lambda_1=3 (см. пункт 4(1) при C_1=1 ), находим три линейно независимых собственных вектора матрицы

$s_1=begin{pmatrix}1\0\-1end{pmatrix}!,qquad s_2=begin{pmatrix}1\-1\0 end{pmatrix}!,qquad s_3=begin{pmatrix}1\1\1end{pmatrix}!.$

Заметим, что для корня lambda_2=0 собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы равно нулю.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Примеры с решением

Пример 2.8.

Пример 2.9.

Элементарные преобразования.

Собственные числа. Собственные векторы матрицы.

Собственные векторы и собственные значения матрицы

Свойства собственных векторов

Нахождение собственных векторов и собственных значений матрицы