|
т.к. это прямоугольник, противоположные стороны у него равны. Следовательно, для вычисления суммы длин его сторон верна формула |
Пример:
измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.
Найдём сумму длин всех сторон этого прямоугольника.
Для этого сложим все эти длины.
Получим:
(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.
Периметр — это сумма длин всех сторон фигуры.
Значит,
складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.
Периметр обозначается заглавной латинской буквой (Р).
Итак,
периметр прямоугольника (Р = 12) см.
Найдём периметр треугольника.
Сначала измерим стороны треугольника.
Длины сторон треугольника равны (4) см, (3) см, (6) см.
Значит,
сумма длин всех сторон треугольника, т. е. периметр треугольника
равен:
(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.
Дан квадрат, длина стороны которого равна (4) см.
У квадрата все стороны равны.
Периметр квадрата равен сумме длин всех сторон квадрата.
Получим:
(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.
Если у треугольника все стороны равны, такой треугольник называется равносторонний.
Для определения периметра данного треугольника найдём сумму длин всех его сторон.
Получим:
(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.
Источники:
Рис. 1. Прямоугольник. © ЯКласс
Рис. 2. Треугольник. © ЯКласс
Рис. 3. Квадрат. © ЯКласс
Рис. 4. Равносторонний треугольник. © ЯКласс
|
Это простой вопрос на знание школьной программы по матетатике. Сумма длин всех сторон геометрической фигуры всегда называлась и называется периметром. Собственно, формула для расчета периметра — это и есть сложение длин всех имеющихся сторон. Длину окружности тоже иногда называют периметром окружности. автор вопроса выбрал этот ответ лучшим 88SkyWalker88 7 лет назад Такое определение подходит для периметра. Периметр можно найти у многих фигур, например, ромб, трапеция или прямоугольник. Просто напросто складываем длину всех сторон фигуры. Для высчитывания периметра есть также разные формулы. Например, периметр квадрата со стороной а будет равняться 4а. Limitless 7 лет назад Если мы зададимся целью просуммировать числовое значение каждой стороны заданной фигуры или определим всю длину круга, то в результате полученное значение будет обозначать всем известный ещё с уроков геометрии Матвей628 9 лет назад Сумма длин всех сторон называется периметром, причем совершенно не важно, к какой именно геометрической фигуре относится это высказывание. Обычно определение периметра, как суммы длин всех сторон геометрической фигуры, относится к плоским геометрическим фигурам, имеющим замкнутый контур – кубу, квадрату, параллелограмму, многоугольнику. В случае трехмерных фигур определить периметр становится сложнее, поскольку одна и та же сторона может относиться к разным граням. Поэтому для трехмерных геометрических фигур обычно применяют понятие периметра грани, где периметром называется сумма длин всех сторон, составляющих одну грань. Rogneda 7 лет назад Если у плоскостной геометрической фигуры, треугольника, квадрата, параллелограмма или любой другой неправильной по форме фигуры, длину каждой стороны можно сложить вместе, то в результате получиться математическая величина, которая называется термином периметр от греческого глагола perimetreo, что буквально значит «измеряю». А греческое существительное perimetron, образованное от указанного глагола, значит «окружность». У круга нет сторон, которые можно измерить, тогда измеряется длина окружности — периметр. Ninaarc 7 лет назад Плоские геометрические фигуры имеют стороны, которые образовывают границы этой фигуры. Сумма всех длин границ геометрической фигуры называется периметром и измеряется в тех же величинах, что и длина. Сложением длин сторон можно определить периметр прямоугольников, треугольников, ромбов, квадратов, трапеций и других фигур, имеющих стороны. Периметр круга называется длиной окружности, которую можно определить по формуле: Но поскольку, сторон в круге нет, то этот случай обычно рассматривается отдельно. Mirra-Mi 7 лет назад Независимо от того какая фигура перед нами лежит, если сложить значения длин всех его сторон, то получим параметр, который называется периметром. Для этого нужно измерить все стороны, если есть неизвестные, то рассчитать, а потом все это сложить воедино. Это может быть стороны треугольника, прямоугольника, квадрата, параллелограмма, ромба и так далее. Virineya 7 лет назад Суммой длин всех сторон называется периметром многоугольника. В некоторых случаях требуется вычислять периметр по особенным формулах, в которых он обозначается как Р и измеряется в: мм, см, м, км. Периметр любой многоугольной фигуры вычисляется сложением длин всех сторон: P(ABCDE) = AB + BC + CD + DE + EA yuliyakotya 7 лет назад Это программа по математике для третьего класса.Можно сказать,что это первая формула,которую учат дети в школе.Сумма длин всех сторон называется периметр.То есть,чтобы найти эту величину,то необходимо сложить длины всех сторон многоугольника,или другой данной фигуры. Leather-Radish 8 лет назад Сумма длин всех сторон еще называют одним словом: периметр. Например, у четерехугольника четыре стороны. Вот если нам известны длины всех сторон, то просто приплюсовав их друг к другу мы получим периметр прямоугольника. Если вспомнит школьный материал, то сумма длин всех сторон будет «периметр». Афанасий44 9 лет назад Ещё со школы помнится, потому что учителя хорошие были, что если сложить длину всех сторон любой плоской геометрической фигуры, то сумма их будет называться периметр. И не имеет значения, какой формы эта фигура — правильная или неправильная Елена Лук 9 лет назад по- моему сумма жлин всех сторон называется периметр Знаете ответ? |
Содержание
- Методическая разработка урока математики в 1-м классе по теме «Длина. Нахождение суммы длин всех сторон многоугольников» (периметр)
- Как найти периметр фигуры
- Определение периметра
- Формулы нахождения периметра
- Равносторонний многоугольник
- Прямоугольник и параллелограмм
- Окружность
- Решение задач
- «Величины. Длина. Нахождение суммы длин всех сторон многоугольников»
- Просмотр содержимого документа ««Величины. Длина. Нахождение суммы длин всех сторон многоугольников»»
Методическая разработка урока математики в 1-м классе по теме «Длина. Нахождение суммы длин всех сторон многоугольников» (периметр)
Цель урока: закрепить знания о величинах и их измерении, полученные на предыдущих уроках.
Задачи:
- Научить измерять длины сторон многоугольников и вычислять периметр закрепление знаний о величинах и их измерении;
- Совершенствование вычислительных навыков, решение задачи по теме “Периметр”;
Учебник Л.Г. Петерсон “Математика для 1 класса”
Поздороваться с гостями!
Чтобы хорошо считать, нужно ум тренировать. Торопись, беги, спеши на урок математики.
1. Сегодня, ребята, мы отправимся в путешествие в удивительную страну ГЕОМЕТРИЮ.
– Как вы думаете, какие жители населяют эту страну? (Точки, отрезки, геометрические тела и фигуры, прямые, лучи, линии, углы…).
Путешествовать будем на паровозике.
(На доске прикреплён паровоз с вагонами).
– Кто будет путешествовать вместе с нами? (Буратино, Винни-Пух, Петушок – Золотой гребешок, Колобок).
Буратино, как вы помните, не дошёл до школы и не научился как следует считать.
Давайте, покажем ему, как вы умеете это делать. Мы поможем Буратино собрать геометрическую фигуру.
2. Устный счёт(с пособиями для счёта)
- Назвать число, последующее 3 (– 4)
- 4 уменьшить на половину (– 2)
- Первое слагаемое – 2, второе – 3. Чему равна сумма? (– 5)
- Уменьшаемое – 5, вычитаемое – 4. Найти разность? (– 1)
- Сколько надо прибавить к 1, чтобы получить 7 (– 6)
- Из каких двух одинаковых слагаемых состоит 6 (– 3)
- На сколько 3 меньше 10 (– 7)
(На доске учитель выкладывает геометрическую фигуру).
– Какая фигура у нас получилась? (прямоугольник, многоугольник, 4-х угольник)
– А какую фигуру напоминают наши вагончики?
На уроке мы встретимся с разными фигурами и узнаем о них что-то новое.
3. Поработает с другим многоугольником.
Тетрадь: стр. 4 №1 (Поможем птичкам разобраться в их споре).
– Рассмотрите многоугольник.
– Как он называется? (АБВГ)
– Как вы думаете: являются ли стороны многоугольника ОТРЕЗКАМИ? (выслушать выводы учащихся)
– А сейчас я покажу фокус – кто из вас прав (модель из полосок 4-х угольника).
– Кто же был прав? (Кто считал, что стороны являются отрезками).
– Давайте измерим стороны.
– Какую величину измерения длины вы знаете? (СМ)
Измеряем стороны и записываем в тетрадях и на доске:
АБ = 1 см
БВ = 5 см
ВГ = 3 см
АГ = 4 см.
– Сравните длины сторон. Что о них можете сказать?
4. Теперь назовите фигуры, которые вы видите в задании № 2.
Квадрат, 4-х угольник, прямоугольник
Многоугольник, 6-ти угольник
– Измерьте стороны квадрата (3 см)
– Что заметили?
– Измерьте стороны треугольника (4 см)
– Что получилось?
– Измерьте стороны последней фигуры (2 см)
– Что заметили сейчас?
– Какой вывод можем сделать? (правильные многоугольники, одинаковой длины стороны)
– А какой вывод можем сделать по 1 и 2 заданию?
5. Итак, мы познакомились с многоугольниками, имеющими разные длины сторон и многоугольниками, имеющими равные длины сторон.
Чтобы продолжить дальше наше путешествие, нам надо немного отдохнуть. А в этом нам поможет тот, кто еде в 3-ем вагоне. (Винни-Пух). Он сочиняет песни и поёт их.
Физкультурная пауза (под музыку).
Теперь пассажир из 3-го вагона предлагает выполнить задание № 3 на стр. 4
– Какая это фигура?
– А попробуйте найти в окружающей обстановке предметы прямоугольной формы (парты, доска, книги, дверь, тетради, пеналы, линейки…)
– Измерим длины сторон этого прямоугольника
– Что заметили?
– Какие стороны равны? Чему равны?
Запишем в тетрадь и на доске
АБ = ВГ = 2 см
БВ = АГ = 4 см
(Ученики записывают на доске).
Семья кенгуру хорошо прыгает, и нам предлагает попрыгать и отдохнуть под музыку.
– А теперь семья кенгуру подскажет, как называется Большая сторона и Меньшая сторона нашей фигуры.
Посмотрите в тетрадь. Как называется большая сторона?
Длина (табличка на доску под вагончики).
– Сколько у нас таких сторон?
– А как называется меньшая сторона?
Ширина (табличка на доску под вагончик).
– Сколько их?
– Как расположены 2 длины и 2 ширины по отношению друг к другу? (одна под другой, напротив)
Противоположные стороны (табличка).
– Повторите по табличкам (хорошо).
6. А давайте попробуем найти сумму длин всех сторон нашего прямоугольника.
– Кто догадался, что это значит “найти сумму длин?” (сложить все стороны).
Запишем на доске: 4 см + 2 см + 4 см + 2 см = 12 см
(По одному на доске).
– Хотите узнать: каким интересным коротким словом называется “сумма длин сторон многоугольника”.
В этом нам помогут пассажиры в вагончиках.
– Поменяйте местами одинаковые вагончики (открываем доску)
– Какое слово получилось? (Периметр)
– А кто запомнил, что это слово означает?
7. Молодцы, хорошо поработали. Можно немного отдохнуть.
Физкультурная минута для глаз.
Следим глазами по указке и произносим, не торопясь, слово “периметр”.
– А теперь закройте глаза, послушайте и доскажите словечко.
Он давно знакомый мой,
Каждый угол в нем прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его…(квадрат)
– А видите ли вы на нашей пиктограмме квадрат? Покажите.
– Посмотрите на свои парты. У вас тоже есть квадраты.
(На партах лежат квадраты – красные, жёлтые, зелёные; цвет с 2-х сторон).
– Найдите периметр ваших квадратов. А что такое периметр? (работа в парах)
– Чему равен периметр?
– А как вы находили? (измеряли; 1 раз измеряли)
– А как же получилось, что у каждого ряда разный цвет квадрата,
А периметр одинаковый?
Вывод: цвет не важен, а важна длина стороны квадрата.
8.
– Можем ли мы сказать, что Периметр – это целое? (на доске модель квадрата)
– Тогда чем будет являться длина каждой стороны фигуры? (частью)
– А теперь займёмся решением геометрической задачи на нахождение части
Стр. 5, №5 (модель треугольника развернуть).
Решение геометрической задачи на нахождение части.
— Работа с текстом задачи;
— Самостоятельное чтение задачи;
— Читает один учащийся.
— Что известно в задаче?
-Чем является периметр в задаче?
— Какие части известны? Что находим? Как?
в) Заполняем схему в тетради и на доске.
г) Решение в тетрадях и на доске: 7-2-2=3 (см)
д) Запись ответа.
А есть другой способ решения 7-(2+2) = 3 (см)
9. Наш паровоз прибыл на конечную станцию. Давайте подведём итог нашего путешествия.
– В какой стране побывали?
– Что нового узнали на уроке? (открытия, выводы)
– Чему научились?
10. Герой путешествия, который похож на геометрическую фигуру, но у неё нельзя узнать периметр, что-то хочет сказать всем вам. (круг – Колобок)
Переворачиваю карточку с вагоном, в котором Колобок, за ним написано – ОТЛИЧНО.
Источник
Как найти периметр фигуры
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
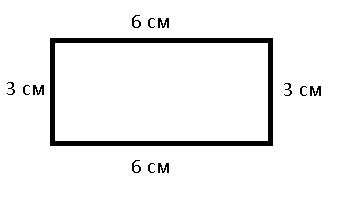
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 +
× 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Источник
«Величины. Длина. Нахождение суммы длин всех сторон многоугольников»

На этом уроке дети научатся измерять длины сторон многоугольников и вычислять периметр, использовать полученные знания и умения в повседневной жизни, а также приобретут навыки работы в паре.
Просмотр содержимого документа
««Величины. Длина. Нахождение суммы длин всех сторон многоугольников»»
Урок математики в 1-м классе по теме
Нахождение суммы длин всех сторон многоугольников»
Цель урока: закреплять знания о величинах и их измерении, полученные на предыдущих уроках; учить вычислять периметр многоугольника; развивать речь, логическое мышление, память, внимание; прививать интерес к математике.
Научить измерять длины сторон многоугольников и вычислять периметр; закрепление знаний о величинах и их измерении.
Работать в паре.
1. Сегодня, ребята, мы отправимся в путешествие в удивительную страну ГЕОМЕТРИЮ.
– Как вы думаете, какие жители населяют эту страну? (точки, отрезки, геометрические тела и фигуры, прямые, лучи, линии, углы, …).
— А чтобы нам было интересно на уроке, и вы могли успешно справиться с заданиями, что надо делать?
— Внимательно слушать вопросы учителя и быстро находить на них ответ.
— Правильно выполнять предложенные задания.
— Оказывать помощь друг другу
— Уметь выслушивать других.
— Активно работать на уроке.
— Молодцы! Я надеюсь, что у нас всё получится.
— Путешествовать будем на поезде.
– Кто будет путешествовать вместе с нами? (Буратино, Винни-Пух, Пятачок, Колобок).


— Буратино, как вы помните, не дошёл до школы и не научился как следует считать.
— Давайте, покажем ему, как вы умеете это делать.
2. Математический диктант (запись чисел на доске и в тетрадях в одну строку – минутка чистописания).
Увеличьте 3 на 5.
Уменьшите 7 на 6.
Первое слагаемое – 2, второе – 3. Чему равна сумма?
Уменьшаемое – 5, вычитаемое – 4. Найти разность?
Вычислите сумму чисел 6 и 2.
Найдите разность чисел 8 и 5.
— Молодцы, хорошо считаете!
— А какую фигуру напоминают наши вагончики?
— На уроке мы встретимся с разными фигурами и узнаем о них что-то новое.
3. Работа по учебнику (с.6 — №1).
– Рассмотрите фигуру. Как она называется? (четырёхугольник, многоугольник, замкнутая ломаная).
— Сколько сторон у многоугольника? (4)
– Как он называется? (АБВГ)
– Как вы думаете: являются ли стороны многоугольника отрезками? (Выводы учащихся)
– Стороны многоугольников измеряют точно так же, как отрезки. Давайте измерим стороны.
– Какую величину измерения длины вы знаете? (см)
— Измеряем стороны, записываем в тетрадях и на доске.
– Сравните длины сторон. Что о них можете сказать?
4. Теперь назовите фигуры, которые вы видите в задании №2.

– Измерьте стороны квадрата. (3 см)
– Что заметили?
– Измерьте стороны треугольника. (4 см)
– Что получилось?
– Измерьте стороны последней фигуры. (2 см)
– Что заметили сейчас?
– Какой вывод можем сделать? (правильные многоугольники, одинаковой длины стороны)
– А какой вывод можем сделать по I и II заданиям?
— Итак, мы познакомились с многоугольниками, имеющими разные длины сторон и многоугольниками, имеющими равные длины сторон.
— Чтобы продолжить дальше наше путешествие, нам надо немного отдохнуть. А в этом нам поможет Винни-Пух.
— Теперь Винни-Пух предлагает выполнить задание №3 на стр.6.
– Какая это фигура? (прямоугольник)
– Попробуйте найти в окружающей обстановке предметы прямоугольной формы. (парты, доска, книги, дверь, тетради, пеналы, линейки, …)
– Измерим длины сторон этого прямоугольника.
– Что заметили?
– Какие стороны равны? Чему равны?
Запишем в тетради и на доске:
АБ = ВГ = 2 см
БВ = АГ = 4 см
— Как называется бОльшая сторона? (длина)
– Сколько у нас таких сторон? (2)
– А как называется мЕньшая сторона? (ширина)
– Сколько их? (2)
– Как расположены 2 длины и 2 ширины по отношению друг к другу? (одна под другой, напротив)
— Это противоположные стороны.
— Что можете сказать о противоположных сторонах? (Они равны)
6. Практическая работа. Работа в паре.
— Возьмите прямоугольники и сравните их по длине и ширине. Как проще это сделать? (наложить друг на друга)
— Что вы выяснили? (Прямоугольники разные по длине, а по ширине одинаковые)
— А давайте попробуем найти сумму длин всех сторон одного из прямоугольников.
– Кто догадался, что это значит “найти сумму длин?” (сложить все стороны).
— Запишем на доске: 4 см + 2 см + 4 см + 2 см = 12 см
– Хотите узнать: каким интересным коротким словом называется «сумма длин всех сторон многоугольника»?
— В математике принято сумму длин сторон многоугольника называть периметром.
— Что же такое периметр? (сумма длин сторон многоугольника)
— Как вы думаете, можно ли вычислить периметр других фигур? Каких? (ответы детей)
— На какую геометрическую фигуру похож Колобок? (круг)
— Можно у него узнать периметр? (нет)
— А зачем нужно находить периметр? (ответы детей)
7. Работа по учебнику – с.6 (№4).
— Молодцы, хорошо поработали. Можно немного отдохнуть.
Физкультминутка для глаз.
– А теперь закройте глаза, послушайте и доскажите словечко.
Он давно знакомый мой,
Каждый угол в нём прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его…(квадрат)
– Посмотрите на свои парты. У вас тоже есть квадрат.
– Найдите периметр квадрата. А что для этого надо сделать? (работа в парах)
– Чему равен периметр квадрата? (5 см)
– А как вы находили? (измеряли 1 раз)
– Можем ли мы сказать, что периметр – это целое?
– Тогда чем будет являться длина каждой стороны фигуры? (частью)
– А теперь решим геометрическую задачу на нахождение части.
9. Наш паровоз прибывает на конечную станцию. Попрощаемся со сказочными героями и подведём итоги нашего путешествия.
– В какой стране побывали? (Геометрия)
– С каким новым математическим словом познакомились? (периметр)
– Как найти периметр? (сложить все стороны)
— Можно ли сказать, что сегодня мы на уроке мы с вами поработали хорошо?
— Довольны ли вы своими результатами?
— Что было сложно? Что было просто и легко?
— Заполним «Лестницу успеха»:
квадратик зелёного цвета – могу объяснить другим, могу научить других;
квадратик жёлтого цвета – я понял, я научился;
квадратик красного цвета – мне ещё нужна помощь.
Источник
«Таблица умножения на 2» — Кнопочка. Устный счёт. Счёт тройками. Таблица сложения. Способ. Смайлик. Найди лишнее слово. Звонок. Что нового узнали на уроке. Замени сумму. Счёт пятёрками. Первичное знакомство с таблицей умножения. Таблица умножения на 2. Замени сумму чисел умножением. Замени сумму чисел. Что такое умножение. Знак умножения. Знакомство с таблицей умножения. Синеглазка.
«Прямоугольник» — Проверьте. Сколько прямых углов у четырехугольников. Соедините фигуры. Геометрия. Длина. Проверьте себя. Сколько квадратов на рисунке. Урок математики 2 класс. Прямоугольник. Тест. Какая фигура лишняя.
«Знакомство с умножением» — Найти произведение. Больше, меньше, равно. Исследуем. Рассуждаем и доказываем. Разминка. Трудные случаи умножения. Составляем и решаем задачу. Задание усложняется. Умножаем и делим. Презентация урока математики, 2 класс. Посчитать количество клеток в каждой лесенке. Вычислительный тренинг. Организационный момент. Рассуждаем. Наблюдаем, сравниваем.
«Определение времени» — Устный счёт. Аня заплатила за открытку 2 рубля. Определить время. Минута. Во сколько утром начинаются у нас уроки. Запишите число, которое состоит из 6 десятков. Расстояние от одной маленькой черточки до другой. Час. Что нам поможет изучить время. Измените вопрос. Молчанка- повторялочка. О чём здесь идёт речь.
«Задачи для 2 класса» — Узнай, почему вымирают малые лебеди. Проверь свои записи. Решение задач. Найди периметр своего бумажного квадрата. Реши устно. «Лебеди летели и на числа сели…». Определите фигуру. Складывание лебедя. Проверь своё решение уравнения. Найди «пёрышко» со своим именем и выполни самостоятельно работу. Решение задач про лебедей и складывание фигурки лебедя. Найди периметр этого треугольника. Квадрат, прямоугольник, ромб, параллелограмм, четырёхугольник.
«Периметр многоугольника 2 класс» — Геометрическое задание. Оценивание. Волшебная строчка ответов. Самостоятельная работа по вариантам. Сумма длин сторон. Графический арифметический диктант. Долгожданный звонок. Периметр. Периметр многоугольника. Задача на смекалку.
Суммой длин всех сторон называется периметром многоугольника. В некоторых случаях требуется вычислять периметр по особенным формулах, в которых он обозначается как Р и измеряется в: мм, см, м, км. Периметр любой многоугольной фигуры вычисляется сложением длин всех сторон:
P(ABCDE) = AB + BC + CD + DE + EA
Плоские геометрические фигуры
имеют стороны, которые образовывают границы этой фигуры. Сумма всех длин границ геометрической фигуры называется периметром
и измеряется в тех же величинах, что и длина. Сложением длин сторон
можно определить периметр прямоугольников, треугольников, ромбов, квадратов, трапеций и других фигур, имеющих стороны.
Треугольник, как следует из названия, представляет собой многоугольник, образованный тремя вершинами, тремя углами и тремя сторонами. простейшая цифра в абсолютном, так как 3 — минимальное количество сегментов, необходимых для разграничения закрытой поверхности, в дополнение к этому треугольник также важен для многих других его свойств и геометрических характеристик, на которых основаны основы геометрии. не деформируемая фигура и является единственным полигоном, к которому он всегда окостенен и в котором всегда можно вписать окружность.
Периметр круга называется длиной окружности
, которую можно определить по формуле:
Но поскольку, сторон в круге нет
, то этот случай обычно рассматривается отдельно.
Если вспомнит школьный материал, то сумма длин всех сторон будет периметр.
Сумма длин всех сторон еще называют одним словом: периметр. Например, у четерехугольника четыре стороны. Вот если нам известны длины всех сторон, то просто приплюсовав их друг к другу мы получим периметр прямоугольника.
Определение. Определяется внешний угол каждого из двух углов, смежных с одним из его внутренних углов относительно расширений сторон угла, поэтому каждый внутренний угол имеет два внешних угла, которые, в отличие от вершины, являются конгруэнтными. Угол, который обращен в сторону.
Свойство Среди характерных особенностей можно упомянуть то, что сумма его внутренних углов равна 180 °. Свойства В каждом треугольнике внешний угол больше любого несмежного внутреннего угла. Каждый внешний угол равен сумме двух несмежных внутренних углов. В каждом треугольнике с главной стороны больший угол противоположный.
Это программа по математике для третьего класса.Можно сказать,что это первая формула,которую учат дети в школе.Сумма длин всех сторон называется периметр.
То есть,чтобы найти эту величину,то необходимо сложить длины всех сторон многоугольника,или другой данной фигуры.
Ещ со школы помнится, потому что учителя хорошие были, что если сложить длину всех сторон любой плоской геометрической фигуры, то сумма их будет называться периметр
. И не имеет значения, какой формы эта фигура — правильная или неправильная
В геометрии критериями конгруэнции треугольников являются постулат и две теоремы, через которые можно продемонстрировать конгруэнтность между треугольниками, если некоторые из их углов или сторон конгруэнтны. Существуют три критерия сравнения. В математике они называются постулатами или аксиомами, и только утверждения, которые, хотя они и не были доказаны, считаются истинными. В математике по теореме мы имеем в виду утверждение, которое показано на амбиции.
Диссертация. Таким образом, два треугольника одинаковы для первый критерий, который мы хотели продемонстрировать. Высота Высота треугольника относительно одной стороны — это сегмент, перпендикулярный стороне, идущей от противоположной вершины. Медианы Медиана — это сегмент, соединяющий вершину с серединой противоположной стороны, разделяющий треугольник на две части той же области. Каждая медиана лежит на две трети ее длины между вершиной и центром тяжести, а другая треть лежит между центром тяжести и срединной средой противоположной стороны медиан в остром треугольнике Медиан в восьмиугольном треугольнике.
Независимо от того какая фигура перед нами лежит, если сложить значения длин всех его сторон, то получим параметр, который называется периметром. Для этого нужно измерить все стороны, если есть неизвестные, то рассчитать, а потом все это сложить воедино. Это может быть стороны треугольника, прямоугольника, квадрата, параллелограмма, ромба и так далее.
В треугольнике по биссектрисе относительно угла мы имеем в виду протяженность полупрямой, которая делит ее на два конгруэнтных угла и соединяет вершину с противоположной стороной. Биссекторные оси в правом треугольнике Оси треугольника прямые, ортогональные сторонам, проходящим через середину.
Одна сторона в четыре раза больше, чем другая, и на 1 см больше, чем третья. Укажите размеры сторон треугольника. Из математики оценка была не хуже двух. Укажите количество учеников, у которых была математическая единица, если класс имел математическое среднее значение 1, 4.
Сумма длин всех сторон называется
периметром, причем совершенно не важно, к какой именно геометрической фигуре относится это высказывание.
Обычно определение периметра, как суммы длин всех сторон
геометрической фигуры, относится к плоским геометрическим фигурам, имеющим замкнутый контур кубу, квадрату, параллелограмму, многоугольнику. В случае трехмерных фигур определить периметр становится сложнее, поскольку одна и та же сторона может относиться к разным граням. Поэтому для трехмерных геометрических фигур обычно применяют понятие периметра грани, где периметром называется сумма длин всех сторон
, составляющих одну грань.
Решение: В классе было 18 учеников и 12 в классе. Сколько мальчиков соревновались, когда четверть конкурентов стояла перед Яном и две трети позади него? Решение: Все участники были. Есть 30 мальчиков и определенное количество девушек. В лыжной подготовке участвовало 28 мальчиков и всех девушек, что составляло 95% всех учеников. Сколько% учеников в классе — девочки?
Решение. В классе 10 девушек, что составляет 25% от 40 учеников. Каменщик установит стену через 30 часов. Два ученика будут строить одну и ту же стену каждые 40 часов. Сколько часов они будут скреплять стену? Решение: вместе они построят стену через 12 часов.
Если у плоскостной геометрической фигуры, треугольника, квадрата, параллелограмма или любой другой неправильной по форме фигуры, длину каждой стороны можно сложить вместе, то в результате получиться математическая величина, которая называется термином периметр
от греческого глагола perimetreo, что буквально значит измеряю.
Два резистора, соединенные последовательно, дают результирующее сопротивление 18 Ом, параллельное 4 Ом. Определите резисторы каждого резистора. Резисторы: резисторы 12 Ом и 6 Ом. Решение: Диагональ 54 имеет 12-угольный угол. На прямоугольной площади размером 12 м и 10 м нам нужен прямоугольный цветник с площадью 8 м2, чтобы его края были равноудалены от краев области.
Два полигона имеют 24 диагональные страницы и 109 диагональных диагоналей. Рассчитайте окружность этого треугольника. Сумма обоих кругов составляет 80 дюймов. Если умножить двузначное число на сумму его цифр, получим произведение. Число десятков заданного числа на 1 больше числа единиц.
А греческое существительное perimetron, образованное от указанного глагола, значит окружность. У круга нет сторон, которые можно измерить, тогда измеряется длина окружности
— периметр.
Это простой вопрос на знание школьной программы по матетатике. Сумма длин всех сторон геометрической фигуры всегда называлась и называется периметром. Собственно, формула для расчета периметра — это и есть сложение длин всех имеющихся сторон. Длину окружности тоже иногда называют периметром окружности.
Укажите длины ребер двух кубов. Сумма длин всех сторон. Геометрическая фигура с тремя сторонами. Прямоугольник со всеми равными сторонами. Распространение без отдыха. Часть прямой только на одном конце. Собственность на Ассамблею. Каковы числа, которые умножаются? Другое свойство умножения. Второй фактор умножения. Как происходит умножение сборки?
Тысячи единиц объединяются по порядку. Мы находим римские цифры, написанные на. Он может быть мысленно. а не только результат падения. Без этого вам не нужно судить. Результат умножения. Линия фракции читается. Одна часть целого. Часть прямой линии с обоих концов. Инструмент, с помощью которого строится круг. Два полугрипы одного и того же происхождения, а не в пролонгации. противоположные стороны. Это показывает нам, сколько частей мы берем из целого.
Такое определение подходит для периметра.
Периметр можно найти у многих фигур, например, ромб, трапеция или прямоугольник. Просто напросто складываем длину всех сторон фигуры.
Для высчитывания периметра есть также разные формулы. Например, периметр квадрата со стороной а
будет равняться 4а
.
Если мы зададимся целью просуммировать числовое значение каждой стороны заданной фигуры или определим всю длину круга, то в результате полученное значение будет обозначать всем известный ещ с уроков геометрии
по- моему сумма жлин всех сторон называется периметр























 × 2 = 36 см;
× 2 = 36 см;