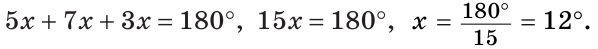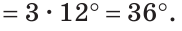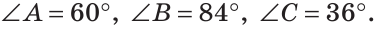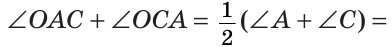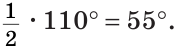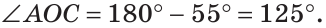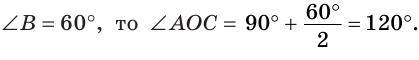Сумма углов треугольника равна (180°).
Доказательство
Рассмотрим произвольный треугольник (KLM) и докажем, что
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
1. Через вершину (L) параллельно стороне (KM) проведём прямую (a).
2. При пересечении параллельных прямых (a) и (KM) секущей (KL), углы, которые обозначаются (1), будут накрест лежащими углами, а углы, обозначенные (2) — это накрест лежащие углы при пересечении этих же параллельных прямых секущей (ML).
Очевидно, сумма углов (1), (2) и (3) равна развёрнутому углу с вершиной (L), т. е.
∠
(1) (+)
∠
(2) (+)
∠
(3 =)
180°
, или
∠
(K) (+)
∠
(L) (+)
∠
(M =)
180°
.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна
90°
.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен
45°
.
Следствие 3. В равностороннем треугольнике каждый угол равен
60°
.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство
Из равенств
∠
(KML) (+)
∠
(BML=)
180°
и
∠
(K) (+)
∠
(L) (+)
∠
(KML =)
180°
получаем, что
∠
(BML =)
∠
(K) (+)
∠
(L).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника (KLM) все углы острые.
У треугольника (KMN) угол (K = 90)
°
.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке (MN) — гипотенуза, (MK) и (KN) — катеты.
У треугольника (KLM) один угол тупой.
Геометрия
7 класс
Урок №23
Сумма углов треугольника
Перечень рассматриваемых вопросов:
- Формулирование и доказательство теоремы о сумме углов треугольника.
- Следствия теоремы о сумме углов треугольника.
- Классификация треугольников по видам углов.
- Формулирование и доказательство теоремы о свойствах прямоугольного треугольника.
- Решение задач с применением пройденного материала;
- Угловой отражатель.
Тезаурус:
Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.
Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.
Сформулируем эту теорему.
Сумма углов треугольника равна 180°.
Дано: ∆АВС.
Доказать:
∠А+∠В +∠С = 180º
Доказательство:
Проведем через вершину В прямую а ║АС.
∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.
Что и требовалось доказать.
Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.
Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Дано: ∆АВС.
Доказать:
∠4 = ∠1 + ∠2.
∠3 + ∠4 = 180° (по свойству развёрнутого угла).
∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.
Что и требовалось доказать.
Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Исходя из этого, можно классифицировать треугольники по углам.
По углам треугольник может быть:
‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);
‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);
‑ прямоугольным, если один угол 90° (т.е. прямой).
В прямоугольном треугольнике стороны имеют свои названия.
Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.
∆АВС– прямоугольный.
∠В = 90°.
АС – гипотенуза.
АВ,ВС – катеты.
Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.
Сумма двух острых углов прямоугольного треугольника равна 90º.
Дано:
∆АВС – прямоугольный.
∠В = 90°.
Доказать: ∠А +∠С = 90°.
Доказательство:
∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°
∠А + ∠С = 180 – 90° = 90°
Что и требовалось доказать.
Решим задачу.
Докажем, что в равностороннем треугольнике каждый угол равен 60 °.
Дано:
∆АВС – равносторонний
Доказать: ∠А =∠С = ∠В = 60°.
Доказательство:
Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.
∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠А = ∠С = ∠В = 180° : 3 = 60°.
Что и требовалось доказать.
Материал для углублённого изучения темы.
Угловой отражатель.
Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.
Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.
Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.
Разбор заданий тренировочного модуля
1. Чему равна градусная мера углаА, если треугольник АВС прямоугольный?
Решение:
По условию, ∆АВС – прямоугольный → сумма его острых углов равна 90°.
∠А+∠В=90°
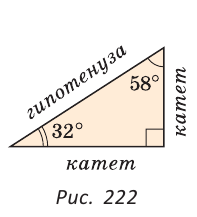
∠В = 45° (по рисунку) →∠А + 45° = 90°.
∠А=90° – 45° = 45°.
Ответ: ∠А = 45°.
2. По рисунку найдите угол N треугольника FNA.
Решение:
По рисунку ∠NAP= 140°, этот угол внешний к углу А треугольника FNA→
∠NAP = ∠N +∠F= 140° (т.к. внешний угол треугольника равен сумме двух углов треугольника не смежных с ним).
∠F = 60° (по рисунку).
∠N + 60° = 140°.
∠N = 140° – 60° = 80°.
Ответ:∠N = 80°.
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
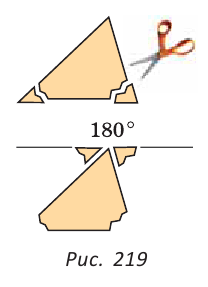
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 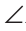
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 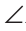
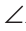
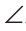
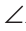





Следствия.
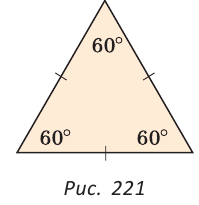
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
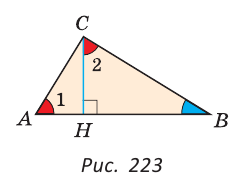
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
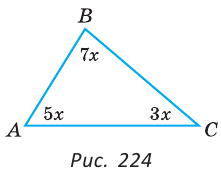
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 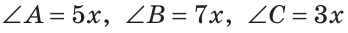
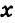
Так как сумма углов треугольника равна 180°, то
Тогда 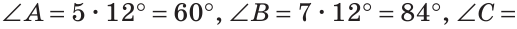
Ответ:
Пример:
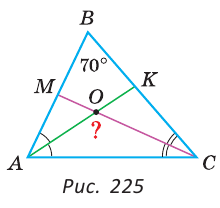
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Ответ: 125°.
Замечание. Если 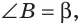
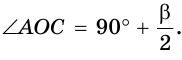
Пример:
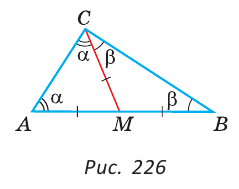
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 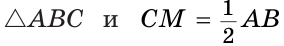
Докажем, что























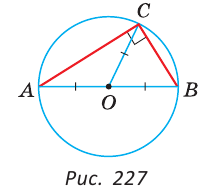
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
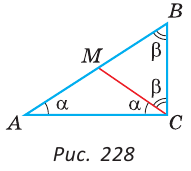
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
Блез
Паскаль, великий французский учёный 17-го века, заметил, что у всех
треугольников сумма 3-х углов равна 180 градусов. И у него возник вопрос: «Как
это доказать?»
И
он отрезал ножницами два уголка треугольника и приложил их к третьему углу. В
результате получился развёрнутый угол, градусная мера которого, как вам уже
известно, равна 180 градусов.
Теорема:
Сумма
углов треугольника равна 180 градусов.
Доказательство:
Пусть
АВС — произвольный треугольник. Доказать, что ∠А+∠В+∠С=
180 градусов.
Проведём
прямую а через точку В параллельно стороне АС.
∠1
и ∠4 — внутренние накрест лежащие углы при параллельных
прямых а и АС и секущей АВ. А значит, ∠1=∠4.
∠3
и ∠5 являются внутренними накрест лежащими при
параллельных прямых а и АС и секущей ВС. Следовательно, ∠3=∠5.
Сумма
градусных мер ∠4, ∠2 и ∠5
равна градусной мере развёрнутого угла с вершиной в точке В, то есть ∠4+∠2+∠5=180
градусов.
А
так как ∠1=∠4,
∠3=∠5,
то получаем, что ∠1+∠2+∠3=180
градусов. То есть ∠А+∠В+∠С=180
градусов. Теорема доказана.
Из
теоремы следует:
1.
Углы равностороннего треугольника равны по 60 градусов.
2.
Сумма острых углов прямоугольного треугольника равна 90 градусов.
Определение:
Внешним
углом треугольника называют угол, смежный с каким-либо
углом треугольника.
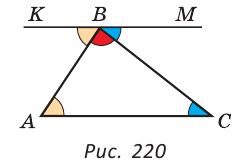
Например,
∠1
— внешний угол треугольника АВС, смежный с ∠ВАС.
∠2
— внешний угол, смежный с ∠АСВ.
Теорема:
Внешний
угол треугольника равен сумме двух внутренних, не смежных с ним.
Доказательство:
Пусть
АВС — произвольный треугольник. Доказать, что градусная мера ∠4
равна сумме градусных мер углов 1 и 2, не смежных с ним.
Сумма
градусных углов 3 и 4 равна градусной мере развёрнутого угла, то есть ∠3+∠4=180
градусов. А по теореме о сумме градусных мер углов треугольника ∠1+∠2+∠3=180
градусов. Из полученных двух равенств следует, что ∠1+∠2=∠4.
Что и требовалось доказать.
Пример.
Стороны
АВ и ВС треугольника АВС равны. ∠А=42
градуса. Чему равна градусная мера угла В?
Так
как АВ=ВС, то треугольник АВС является равнобедренным. Нам известно, что углы
при основании равнобедренного треугольника равны. А значит, ∠С=42
градуса.
По
теореме о сумме углов треугольника ∠А+∠В+∠С=180
градусов. Из этого равенства получаем:
Пример.
На
рисунке ∠ВСD=110 градусов, а ∠ВАС=45
градусов. Найти градусную меру ∠АВЕ.
Так
как углы ВСD
и ВСА — смежные, то:
Тогда:
Искомый
∠АВЕ
является внешним углом нашего треугольника, смежным с ∠АВС.
А значит:
Пример.
В
равнобедренном треугольнике АВС с основанием АС отрезок ВD является высотой. Найдите
градусные меры углов треугольника ABD, если ∠АВС=56
градусов.
Так
как треугольник АВС — равнобедренный, то высота ВD, проведённая к основанию, является
также и биссектрисой. Значит:
∠АDВ=90 градусов, так как ВD —
высота.
По
теореме о сумме углов треугольника, получаем: