Как найти сумму углов фигуры

Была ли эта статья полезной?

В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.

Поговорим подробнее о видах многоугольников и их характеристиках.

При изучении темы, что такое многоугольники, применяются следующие термины:

• Вершины многоугольника.
• Стороны замкнутой ломаной.
• Углы, образованные между смежными сторонами.
• Отрезки между несмежными вершинами называются диагоналями.
• Сумма длин всех сторон фигуры является периметром.
• Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.

Наименования данных фигур зависят от количества сторон:

• Треугольник – это 3 стороны.
• Четырехугольник имеет 4 стороны.
• Пятиугольник – это 5 сторон и пр.

Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.

Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.

Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.

Виды многоугольников

Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.

Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.

Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.

Что такое правильные многоугольники

Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.

На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали

Периметром многоугольника называется сумма длин его сторон.

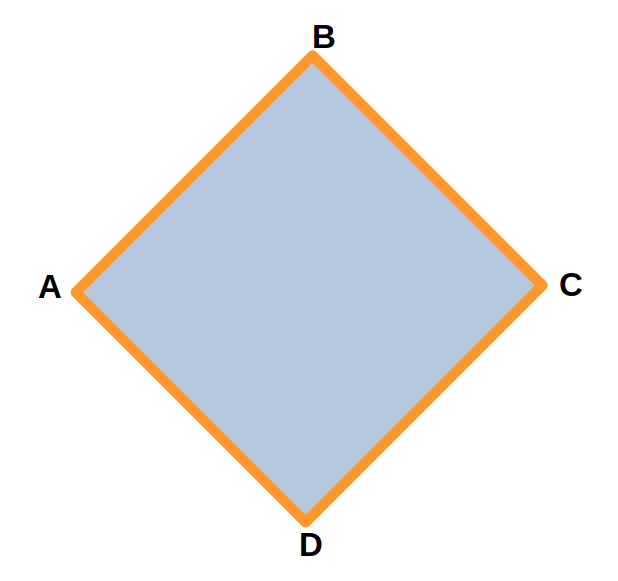
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.

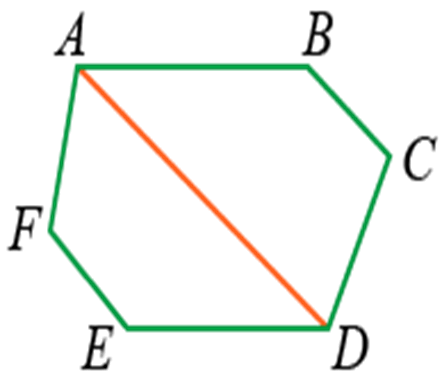
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.

Например, отрезок AD будет являться диагональю фигуры ABCDEF:

Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.

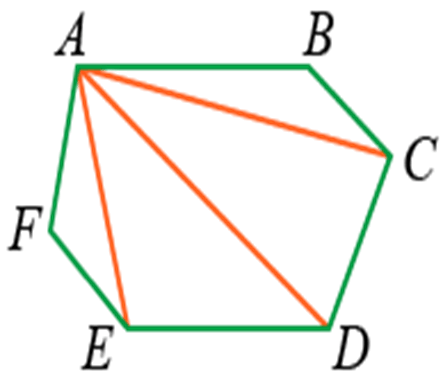
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:

Количество треугольников будет на 2 меньше, чем число сторон:

Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.

Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.

Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

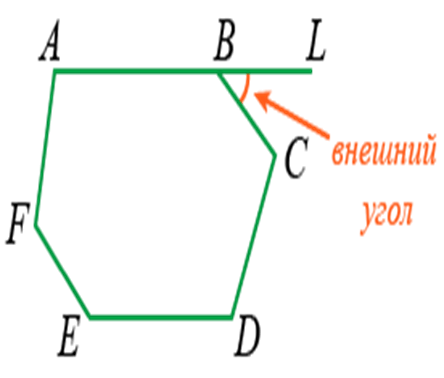
Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

• сумма углов – s;
• число сторон – n;
•  два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Сумма внешних углов

Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.

Где:

• s — сумма внешних углов;
• 4d — четыре прямых угла (4 · 90 = 360°).

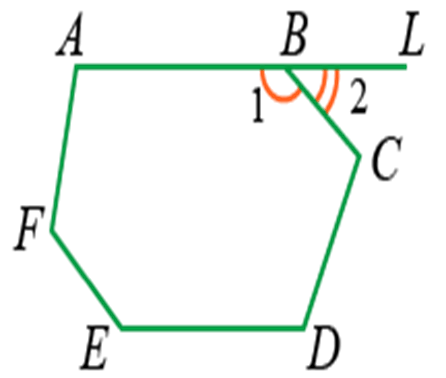
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).

Например, ∠1 и ∠2:

Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.

Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.

Углы многоугольника

• Сумма внутренних углов
• Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например,  ∠ABC  является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например,  ∠LBC  является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n — 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

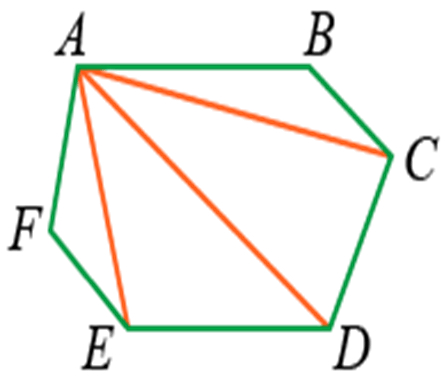
Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Лев Емельянов
«Квантик» №3, 2020

Для математического уха разговор выглядит комично. То, что сумма углов треугольника равна 180°, знают даже школьники, не очень увлечённые математикой. А что такое 180° и почему именно 180? Ясно, скажет умный школьник, это половина от 360, то есть полного оборота.

Невозможно точно сказать, почему окружность была разбита на 360 одинаковых частей и когда это произошло. То ли это персы придумали, у которых год длился 360 дней, то ли вавилоняне, которым удобно было делить окружность на 6 равных частей с помощью равностороннего треугольника.

Была, правда, попытка ввести более логичную, с точки зрения современных представлений о счёте, шкалу для угловых мер. Она делила окружность на 400 равных частей — градов. В этой шкале величина прямого угла равнялась 100 градам. Однако шкала эта не прижилась. Трудно одним желанием изменить пятитысячелетнюю историю цивилизации. Да впрочем, какая разница, в чём мерить, хоть в попугаях, главное — понять, что угол — это некоторая доля от полного оборота.

Почему же сумма углов любого треугольника равна в точности половине полного оборота? Давайте представим себе, что у нас есть три прожектора. Каждый освещает внутренность некоторого угла до бесконечности (жить мы будем временно в двумерном мире). Если мы, стоя в одной точке, включим три прожектора (зелёный, розовый и жёлтый на рисунке), сумма «световых углов» которых равна 180°, и направим их без наложений освещаемой площади, то осветим ровно половину нашего двумерного пространства.

Теперь рассмотрим произвольный треугольник и в вершинах его поставим трёх помощников (Али, Бен и Сирил по буквам вершин, но можно попросить Анну, Варвару и Светлану), доверив им по прожектору. Каждый помощник должен осветить внутренность треугольника лучами света, которые выходят из вершины и продолжаются до бесконечности. Таким образом, каждый прожектор будет освещать внутренность своего угла и не будет освещать внутренность такого же угла, вертикального выбранному. При этом каждая точка плоскости либо попадёт внутрь освещённого угла, либо не будет освещена, попав в вертикальный угол к углу треугольника. Точки же самого треугольника будут освещены трижды. Теперь давайте посмотрим на нашу частично освещённую плоскость с большой высоты (мы-то, как люди трёхмерные, имеем на это право). Если закрыть глаза на небольшой участок перекрытия внутри треугольника, то нетрудно понять, что мы осветили «ровно» половину плоскости. Из чего и можно заключить, что сумма углов произвольного треугольника равна 180°!

Если наше маленькое жульничество внутри треугольника режет глаз, давайте отойдём далеко-далеко от плоскости и забудем, что где-то стоят наши помощники. Нарисуем окружность огромного радиуса с центром где-то внутри треугольника. Какая часть окружности освещена? Ровно (почти) половина. И чем больше радиус нашей окружности, тем меньше будут отличаться освещённая и тёмная части окружности. Ведь каждой светлой дуге будет в пару поставлена такая же тёмная.

Не будем останавливаться на сумме углов треугольника, а попробуем развить эту идею. Самое естественное продолжение — четырёхугольник. Нетрудно понять, что четыре помощника, выполняя аналогичное задание, осветят всю плоскость, что значит: сумма углов четырёхугольника равна 360°. Стоп! Давайте не торопиться, отойдём подальше. Что мы видим? Ужас! Некоторые точки плоскости вообще не освещены. Всё пропало? Не будем паниковать преждевременно. Продолжим наши прямые до бесконечности. На рисунке серым цветом закрашена неосвещённая часть плоскости. Посмотрим внимательно на вертикальный с ней угол. Он освещён, конечно, но освещён дважды! А значит, и здесь всё сходится. Так и должно быть, ведь четырёхугольник можно просто разрезать на два треугольника. Думаем дальше.

Нарисуем пятиконечную звёздочку (не обязательно правильную). Теперь позовём пять фонарщиков, поставим их в вершинах «лучиков» нашей звёздочки, и пусть каждый освещает внутренность того угла, в котором стоит. Соответственно, вертикальный угол освещён не будет. Что мы видим? Картина почти такая же, как у треугольника. Половина плоскости светлая, половина тёмная, а значит, сумма углов пятиконечной звезды равна 180°!

При этом мы нигде не пользовались какими-то особенностями формы этой звёздочки. Более того, а где мы считали количество углов? Давайте внимательно посмотрим на 7-конечную звезду. А потом на 2021-конечную (нарисовать непросто, а представить можно). Что изменится для суммы? Да ничего — половина светлого, половина тёмного. Правда, для большого числа углов нужно «правильно» рисовать звёздочку. Например, для семиугольной конструкции можно привести два примера. Подсчитайте самостоятельно сумму для «более тупоугольной» звёздочки.

Теперь давайте немного развернём наших фонарщиков и дадим им задание осветить один из своих внешних углов. Для начала позовём четверых, поставим их в вершинах выпуклого четырёхугольника. Нетрудно понять, что они осветят всё, кроме самого четырёхугольника. Удаляясь от них, мы поймём, что сумма внешних углов выпуклого четырёхугольника равна 360°.

Также при достаточном удалении мы забудем о количестве помощников, а когда вспомним, поймём, что это совершенно неважно. Сколько бы их ни было, плоскость будет освещена полностью и без перекрытий. Из этого следует чрезвычайно важный и удивительный вывод: сумма внешних углов выпуклого многоугольника равна 360°!

Продолжая применять этот метод, можно получить и другие формулы для суммы углов. То есть если внимательно посмотреть на количество перекрытий, можно вывести формулу для суммы углов выпуклого многоугольника. Но даже без вывода становится понятно, почему сумма внутренних углов зависит от их количества, а сумма внешних нет. Попробуйте развить эту идею на случай невыпуклых многоугольников. Можно, немного поломав голову, найти сумму внутренних углов, а вот для суммы внешних надо сначала понять: что такое внешний угол невыпуклого многоугольника? Успехов в вашем исследовании!

P. S. А угольник 45°, 60° и 90°, оказывается, существует! Это специальный портновский угольник — треугольник, в котором сделаны треугольные дырки с другими углами. И речь в магазине «Ткани», оказывается, совсем не шла о сумме углов треугольника.

Художник Алексей Вайнер

Примечание. Данный материал содержит теорему и ее доказательство, а также ряд задач, иллюстрирующих применение теоремы о сумме углов выпуклого многоугольника на практических примерах.

Теорема о сумме углов выпуклого многоугольника

Для выпуклого n-угольника сумма углов равна 180°(n-2).

Доказательство.

Для доказательства теоремы о сумме углов выпуклого многоугольника воспользуемся уже доказанной теоремой о том, что сумма углов треугольника равна 180 градусам.

Пусть A 1 A 2…  A n – данный выпуклый многоугольник, и n  > 3. Проведем все диагонали многоугольника из вершины A 1. Они разбивают его на n  – 2 треугольника: Δ  A 1 A 2 A 3, Δ  A 1 A 3 A 4, … , Δ  A 1 A n  – 1 A n . Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число треугольников – ( n  – 2). Поэтому сумма углов выпуклого n -угольника A 1 A 2…  A n равна 180° ( n  – 2).

Задача.

В выпуклом многоугольнике три угла по 80 градусов, а остальные — 150 градусов. Сколько углов в выпуклом многоугольнике?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма углов равна 180°(n-2).

Значит, для нашего случая:

180(n-2)=3*80+x*150, где

3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит обозначим их количество как x.

Однако, из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то  очевидно, что x=n-3.

Таким образом уравнение будет выглядеть так:

180(n-2)=240+150(n-3)

Решаем полученное уравнение

180n — 360 = 240 + 150n — 450

180n — 150n = 240 + 360 — 450

30n = 150

n=5

Ответ: 5 вершин

Задача.

Какое количество вершин может иметь многоугольник, если величина каждого из углов менее 120 градусов?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех углов равна 180°(n-2).

Значит, для нашего случая необходимо сначала оценить граничные условия задачи. То есть, сделать допущение, что каждый из углов равен 120 градусам. Получаем:

180(n-2)=120n

180n — 360 = 120n

180n — 120n = 360 (это выражение рассмотрим отдельно ниже)

60n = 360

n=6

Исходя из полученного уравнения, делаем вывод: при величине углов менее 120 градусов, количество углов многоугольника менее шести.

Объяснение:

Исходя из выражения 180n — 120n = 360 , при условии, что вычитаемое правой части будет менее 120n, разность должна быть более 60n. Таким образом, частное от деления всегда будет менее шести.

Ответ: количество вершин многоугольника будет менее шести.

Задача

В многоугольнике три угла по 113 градусов, а остальные равны между собой и их градусная мера — целое число. Найти количество вершин многоугольника.

Решение.

Для решения данной задачи воспользуемся теоремой о сумме внешних углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех внешних углов равна 360°.

Таким образом,

3*(180-113)+(n-3)x=360

правая часть выражения — сумма внешних углов, в левой части сумма трех углов известна по условию, а градусная мера остальных (их количество, соответственно n-3, так как три угла известны) обозначена как x.

201+(n-3)x=360

(n-3)x=159

159 раскладывается только на два множителя 53 и 3, при чем 53 — простое число. То есть других пар множителей не существует.

Таким образом, n-3 = 3, n=6, то есть количество углов многоугольника — шесть.

Ответ: шесть углов

Задача

Докажите, что у выпуклого многоугольника может быть не более трех острых углов.

Решение

Как известно, сумма внешних углов выпуклого многоугольника равна 360⁰. Проведем доказательство от противного. Если у выпуклого многоугольника не менее четырех острых внутренних углов, следовательно среди его внешних углов не менее четырех тупых, откуда следует, что сумма всех внешних углов многоугольника больше 4*90⁰ = 360⁰. Имеем противоречие. Утверждение доказано.

0
 

 Шестиугольник и его свойства |

Описание курса

| Стереометрия