Как найти сумму углов многоугольника 8 класс

Была ли эта статья полезной?

Углы многоугольника

• Сумма внутренних углов
• Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например,  ∠ABC  является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например,  ∠LBC  является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n — 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Предварительная подготовка к уроку: учащиеся должны знать следующие темы: «Многоугольник», «Выпуклый многоугольник».

Цели урока: 1) образовательная: формирование новых знаний по данной теме, умение применять при решении задач; 2) воспитательная: формирование культуры личности, отношение к математике как части общечеловеческой культуры; 3) развивающая: развитие логического мышления, пространственного воображения.

Тип урока: урок изучения нового материала.

Вид урока: урок-лекция.

Ход урока

1. Объяснение нового материала.

Известно, что сумма углов выпуклого n-угольника равна 180°(n – 2). Оказывается, что это утверждение справедливо и для невыпуклых многоугольников.

Рассмотрим самопересекающиеся ломаные. Будем называть их звездчатыми многогранниками.

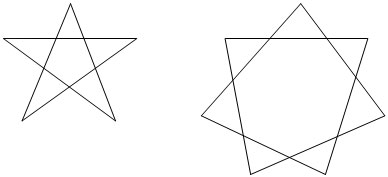
Зафиксируем направление подсчета углов против часовой стрелки. Заметим, что углы, образованные замкнутой ломаной, зависят от направления ее обхода. Если направление обхода ломаной меняется на противоположное, то углами многоугольника будут углы, дополняющие углы исходного многоугольника до 360°.

Если М – многоугольник, образованный простой замкнутой линией, которая проходит в направлении по часовой стрелке, то сумма углов этого многоугольника будет равна 180°(n  –  2). Если же ломаная проходит в направлении против часовой стрелки, то сумма углов будет равна 180°(n + 2).

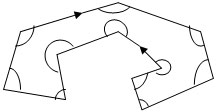
Таким образом, общая формула суммы углов многоугольника, образованного простой замкнутой ломаной, имеет вид ∑ = 180°(n ± 2), ∑ – сумма углов, n – число углов многоугольника, плюс или минус берется в зависимости от направления обхода ломаной.

Наша задача состоит в том, чтобы вывести формулу суммы углов произвольного многоугольного, образованного замкнутой (возможно самопересекающейся) ломаной. Для этого введем понятие степени многоугольника.

Степенью многоугольника называется число оборотов, совершаемое точкой при полном последовательном обходе его сторон. Причем обороты, совершаемые в направлении против часовый, считаются со знаком « + », а обороты по часовой стрелке – со знаком « – ».

У многоугольника, образованного простой замкнутой ломаной, степень +1 или -1 в зависимости от направления обхода. Степень звездчатых семиугольников, изображенных выше, равна соответственно двум и трем.

Теорема. Для произвольного многоугольника имеет место формула ∑ = 180°(n + 2m), где ∑ – сумма углов, n – число углов, m – степень многоугольника.

Доказательство. Пусть многоугольник М имеет степень m. М₁, М₂, …, М_k  – простые замкнутые ломаные, проходя по которым точка совершает полные обороты. А₁, А₂, …, А_k  – соответствующие точки самопересечения ломаной, не являющиеся ее вершинами.

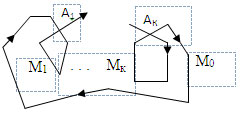
Обозначим число вершин многоугольника М, входящих в многоугольники М₁, М₂, …, М_k, через n₁, n₂, …, n_k соответственно. Поскольку, помимо вершин многоугольника М, к этим многоугольникам добавляются еще вершины А₁, А₂, …, А_k, то число вершин многоугольников М₁, М₂, …, М_k будет равно соответственно n₁ + 1, n₂ + 1, …, n_k+ 1. Тогда суммы этих углов будут равны 180°(n1 + 1 ± 2), 1800(n2 + 1 ± 2), …, 180°(nk + 1 ± 2). Плюс или минус берется в зависимости от направления обхода ломаных.

В качестве примера рассмотрим вычисление суммы углов пятиконечной звездочки. Степень соответствующей замкнутой ломаной равна -2. Поэтому искомая сумма углов равна 180°.

Сумма углов выпуклого многоугольника М0, оставшегося от многоугольника М после удаления многоугольников М₁, М₂, …, М_k равна 180°(n – n₁ – n₂  – … – n_k + k ± 2).

Суммы углов многоугольников М₀, М₁, М₂, …, М_k дают сумму углов многоугольника М, и в каждой вершине А₁, А₂, …, А_k дополнительно получим 360°.

Следовательно, имеем равенство 180°(n₁ + 1 ± 2) + … + 180°(n_k + 1 ± 2) + 180°(n – n₁ – n₂ – … – n_k + k ± 2) = ∑ + 360°k. Приводя подобные члены, получим ∑ = 180°(n ± 2 ± … ±2) = 180°(n + 2m), где m – степень многоугольника  М.

2. Решение задач.

1) Сумма углов выпуклого многоугольника равна 900°. Сколько у него сторон?

2) Найти сумму углов семиконечной звездочки, изображенной выше.

3. Итог урока.

Обратить внимание учащихся на введение новых понятий (звездчатый многоугольник, степень многоугольника), формулу для нахождения суммы углов произвольного многоугольника.

4. Домашнее задание.

1) Теория (конспект урока).

2) Составить две задачи по заданной теме.

В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.

Поговорим подробнее о видах многоугольников и их характеристиках.

При изучении темы, что такое многоугольники, применяются следующие термины:

• Вершины многоугольника.
• Стороны замкнутой ломаной.
• Углы, образованные между смежными сторонами.
• Отрезки между несмежными вершинами называются диагоналями.
• Сумма длин всех сторон фигуры является периметром.
• Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.

Наименования данных фигур зависят от количества сторон:

• Треугольник – это 3 стороны.
• Четырехугольник имеет 4 стороны.
• Пятиугольник – это 5 сторон и пр.

Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.

Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.

Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.

Виды многоугольников

Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.

Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.

Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.

Что такое правильные многоугольники

Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.

На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали

Периметром многоугольника называется сумма длин его сторон.

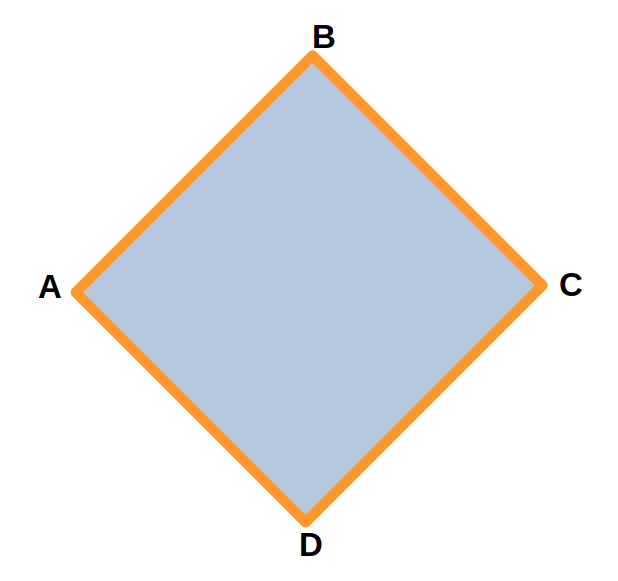
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.

Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.

Например, отрезок AD будет являться диагональю фигуры ABCDEF:

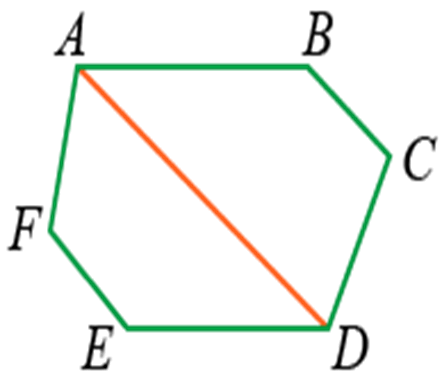
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.

Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:

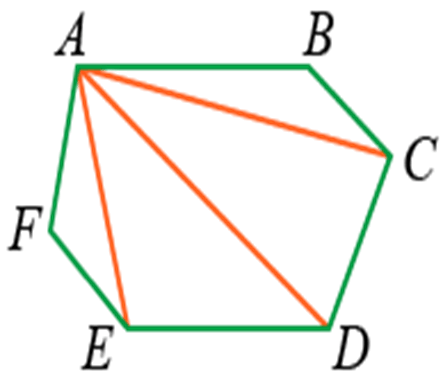
Количество треугольников будет на 2 меньше, чем число сторон:

Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.

Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.

Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

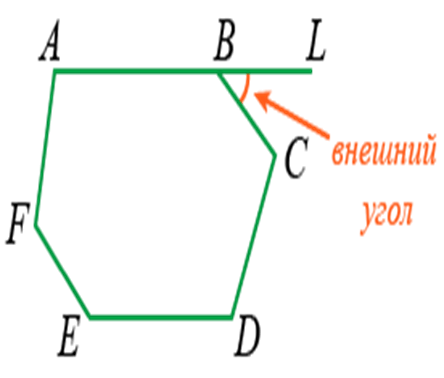
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

• сумма углов – s;
• число сторон – n;
•  два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

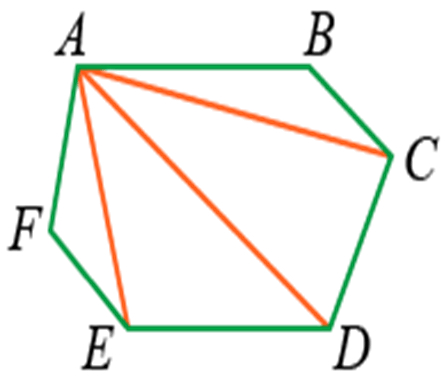
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Сумма внешних углов

Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.

Где:

• s — сумма внешних углов;
• 4d — четыре прямых угла (4 · 90 = 360°).

Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).

Например, ∠1 и ∠2:

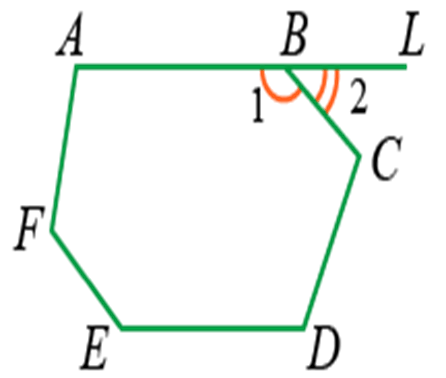
Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.

Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.

Теорема

(о сумме углов выпуклого многоугольника)

Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

(n — количество сторон многоугольника).

Другой вариант формулировки этой теоремы:

Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

Дано:

   

—  выпуклый n -угольник.

Доказать:

   

   

Доказательство:

1-й способ

Обозначим внутри многоугольника произвольную точку O.

Соединим точку O с вершинами многоугольника.

Получили n треугольников.

   

   

   

Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.

Так как сумма углов при вершине O составляет 360º

   

то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

Сумма углов каждого треугольника равна 180º.

Таким образом, искомая сумма углов n угольника равна

   

   

Что и требовалось доказать.

2-й способ

Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

Сумма всех углов этих треугольников равна сумме углов многоугольника.

Сумма углов углов каждого из треугольников равна 180º.

Следовательно, сумма углов многоугольника

   

   

Что и требовалось доказать.