Содержание:
- § 1 Теорема о сумме углов треугольника
- § 2 Прямоугольный, остроугольный и тупоугольный треугольники
- § 3 Краткие итоги урока
§ 1 Теорема о сумме углов треугольника
Треугольник — одна из самых распространенных фигур в геометрии. Вениамин Фёдорович Каган, русский математик ХХ века, однажды сказал: «Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике…» действительно одна из важнейших теорем геометрии гласит
Теорема: Сумма углов в треугольнике равна 180 градусов.
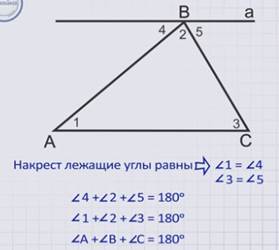
Докажем эту теорему. Для этого возьмем произвольный треугольник АВС. Через вершину В проведем прямую а параллельную стороне треугольника АС. Пронумеруем получившиеся углы: 1,2,3 номера углов при вершинах А, В и С соответственно, углы 4 и 5 образованы прямой а и сторонами АВ и ВС треугольника. Первый и четвертый углы являются накрест лежащими при пересечении параллельных прямых АС и а секущей АВ. Согласно теореме о накрест лежащих углах, они равны, то есть первый угол равен четвертому. Аналогично третий угол равен пятому, так как являются накрест лежащими при пересечении параллельных а и АС секущей ВС.
Сумма углов 4, 2 и 5 представляют собой развернутый угол с вершиной В, а он, как известно, равен 180 градусам. Тогда, исходя из равенства углов 1 и 4, 3 и 5, получаем, что сумма первого, второго и третьего углов равна 180 градусам. То есть угол А плюс угол В плюс угол С равно 180 градусов.
Что и требовалось доказать.
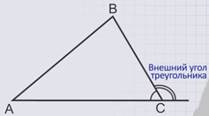
А теперь продлим сторону АС треугольника АВС и рассмотрим смежный угол угла С, такой угол называется – внешним углом треугольника.
Поскольку смежные углы составляют развернутый угол, их сумма равна 180 градусам, тогда внешний угол треугольника равен 180 градусов минус угол С. А нам теперь известно, что сумма углов треугольника равна 180 градусам, и из этой теоремы следует, что 180 градусов минус угол С — это сумма углов А и В. Значит, величина внешнего угла треугольника равна сумме двух углов треугольника не смежных с ним.
§ 2 Прямоугольный, остроугольный и тупоугольный треугольники
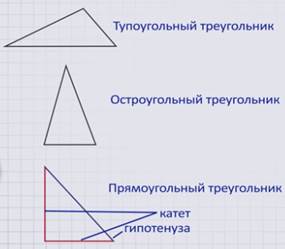
Представим, что в треугольнике один угол 90 градусов, тогда, согласно теореме о сумме углов в треугольнике, сумма оставшихся двух углов должна быть равна 180 — 90 = 90 градусам, из чего следует, что оставшиеся углы острые. Если же в треугольнике есть тупой угол, то есть больше 90 градусов, то оставшиеся два углы в сумме должны быть меньше 90 градусов и, значит, также будут острыми. Таким образом, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой. Поэтому в зависимости от вида угла рассматриваемый треугольник может быть:тупоугольным, если среди его углов есть тупой угол, остроугольным, если все три угла треугольника острые, или прямоугольным, если в треугольнике есть угол, равный 90 градусам.
В прямоугольном треугольнике стороны, расположенные друг к другу под прямым углом, называют катетами, а сторону, расположенную напротив угла в 90 градусов, гипотенузой.
§ 3 Краткие итоги урока
Итак, сумма углов в треугольнике равна 180 градусам.
Угол смежный с углом при вершине треугольника называется внешним углом треугольника и равен сумме двух углов треугольника не смежных с ним.
Треугольники могут быть трёх видов: остроугольные, тупоугольные и прямоугольные.
Список использованной литературы:
- Атанасян, Л.С. Учебник: Геометрия. 7-9 классы: учеб. для общеобразоват. организаций/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. –383 с.
- Геометрия. Ч.I. Планиметрия: учебное пособие/ И.Б. Барский, Г.Н. Тимофеев. – Йошкар-Ола: изд-во Марийского гос. ун-та, 2006 и 2008. – 636с.
Главная > Геометрия 7 класс > Сумма углов треугольника
Сумма углов треугольника — видеоурок
На этом видео уроке по геометрии для 7 класса объясняется чему равна сумма углов в треугольнике, решаются задачи из учебника Атанасяна
Внешний угол треугольника
Внешний угол треугольника – это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны ( как вертикальные).
Записываем в тетрадь:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°
Изучите видео ролик ниже:
Видео YouTube
Практическая часть занятий:
Решение задач на отыскание величин треугольника по теореме о сумме углов треугольника и внешнем угле. Теоремы обязательно выучить и видео внимательно все разобрать:
Видео YouTube
Геометрия. 7 класс
Конспект урока
Сумма углов треугольника
Перечень рассматриваемых вопросов:
- Формулирование и доказательство теоремы о сумме углов треугольника.
- Следствия теоремы о сумме углов треугольника.
- Классификация треугольников по видам углов.
- Формулирование и доказательство теоремы о свойствах прямоугольного треугольника.
- Решение задач с применением пройденного материала;
- Угловой отражатель.
Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.
Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.
Сформулируем эту теорему.
Сумма углов треугольника равна 180°.
Проведем через вершину В прямую а ║АС.
∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.
Что и требовалось доказать.
Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.
Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠3 + ∠4 = 180° (по свойству развёрнутого угла).
∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.
Что и требовалось доказать.
Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Исходя из этого, можно классифицировать треугольники по углам.
По углам треугольник может быть:
‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);
‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);
‑ прямоугольным, если один угол 90° (т.е. прямой).
В прямоугольном треугольнике стороны имеют свои названия.
Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.
Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.
Сумма двух острых углов прямоугольного треугольника равна 90º.
∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°
∠А + ∠С = 180 – 90° = 90°
Что и требовалось доказать.
Докажем, что в равностороннем треугольнике каждый угол равен 60 °.
Доказать: ∠А =∠С = ∠В = 60°.
Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.
∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠А = ∠С = ∠В = 180° : 3 = 60°.
Что и требовалось доказать.
Материал для углублённого изучения темы.
Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.
Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.
Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.
Разбор заданий тренировочного модуля
1. Чему равна градусная мера углаА, если треугольник АВС прямоугольный?
По условию, ∆АВС – прямоугольный → сумма его острых углов равна 90°.
2. По рисунку найдите угол N треугольника FNA.
По рисунку ∠NAP= 140°, этот угол внешний к углу А треугольника FNA→
∠NAP = ∠N +∠F= 140° (т.к. внешний угол треугольника равен сумме двух углов треугольника не смежных с ним).
Виды треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный видеоурок предназначен для самостоятельного ознакомления с темой «Виды треугольников». При помощи него все желающие смогут получить представления о том, что представляет собой треугольник, какие существуют виды этой геометрической фигуры. Также учитель расскажет об одной из важнейших теорем – сумме углов треугольника.
http://resh.edu.ru/subject/lesson/7308/conspect/
http://interneturok.ru/lesson/geometry/7-klass/sootnosheniya-mezhdu-storonami-i-uglami-treugolnikov/vidy-treugolnikov
Как поступить
в Онлайн-школу и получить аттестат?
Подробно расскажем о том, как перевестись на дистанционный формат обучения, как устроены онлайн-уроки и учебный процесс, как улучшить успеваемость и повысить мотивацию!
Нажимая на кнопку, я соглашаюсь на обработку
персональных данных
- Все предметы
- 7 класс
- Геометрия
-
Сумма углов треугольника
-
Общие геометрические сведения
-
Геометрические построения
- Видеоурок
- Учебник
- Тест
Видеоурок: Сумма углов треугольника
Треугольники
-
Видеоурок 15. Геометрия 7 класс
Предыдущий урок
Третий признак равенства треугольников
Треугольники
Следующий урок
Второй признак равенства треугольников
Треугольники
-
Деепричастный оборот
Русский язык
-
Паразитические плоские черви
Биология
-
Вынесение общего множителя за скобки
Алгебра
Зарегистрируйся, чтобы присоединиться к обсуждению урока
Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.
Отзывы об уроке:
Пока никто не оставил отзыв об этом уроке