Как найти сумму в циклическом алгоритме - Исправление недочетов и поиск решений вместе с Examum.ru

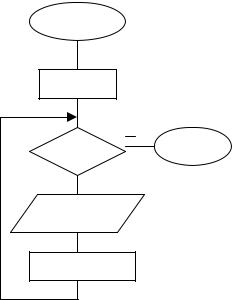
Рис.9. Алгоритм вычисления корней уравнения X2+B*X+C=0

Задания для самостоятельного выполнения

Составить визуальные разветвленные алгоритмы для следующих задач.

1.Для двух чисел Х,У определить, являются ли они корнями уравнения А*Р^4+D*P^2+C=0

2.Если среди трех чисел А,В,С имеется хотя бы одно четное вычислить максимальное, иначе — минимальное 3.Ввести положительное А>=1. Найти наибольшее из выражений вида 1А и SIN(A).

4.Ввести два числа . Меньшее заменить полусуммой, а большее — удвоенным произведением. 5.Ввести три числа А,В,С . Удвоить каждое из них , если А>=В>=С, иначе поменять значения А и В.

6.Определить является ли точка с координатами X,Y точкой пересечения диагоналей квадрата со стороной R ,одна вершина которого расположена в начале координат.

7.* Определить значения функции в зависимости от значения аргумента

	а*х2 ,	если х > 10
у=	1/х ,	если –10 ≤ х ≤ 10
	Sin(х) , если х < 10

7.ЦИКЛИЧЕСКИЕ АЛГОРИТМЫ

Циклические алгоритмы являются наиболее распространенным видом алгоритмов, в них предусматривается повторное выполнение определенного набора действий при выполнении некоторого условия. Такое повторное выполнение часто называют циклом.

Существуют два основных видов циклических алгоритмов: циклические алгоритмы с предусловием, циклические алгоритмы с постусловием. Они отличаются друг от друга местоположением условия выхода их цикла.

Цикл с предусловием начинается с проверки условия выхода из цикла. Это логическое выражение, например I<=6. Если оно истинно, то выполняются те действия, которые должны повторяться. В противном случае, если логическое выражение I<=6 ложно, то этот цикл прекращает свои действия.

Цикл с постусловием функционирует иначе. Сначала выполняется один раз те действия, которые подлежат повторению, затем проверяется логическое выражение , определяющее условие выхода из цикла, например, I>6

.Проверка его осуществляется тоже по-другому. Если условие выхода истинно, то цикл с постусловием прекращает свою работу, в противном случае — происходит повторение действий, указанных в цикле. Повторяющиеся действия в цикле

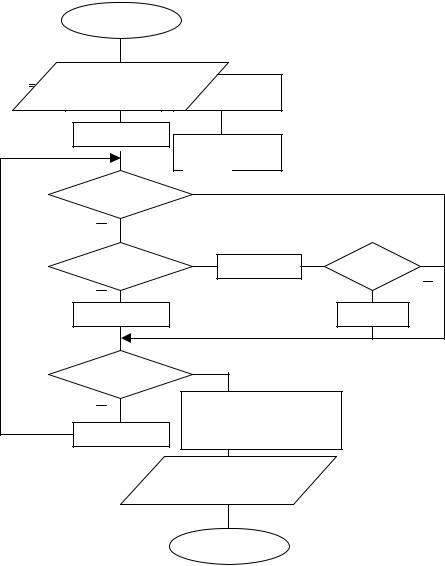
называются «телом цикла».Разновидности циклов приведены на рис. 10а),б).

i=1

K:=K+1

I<=6

i:=i+0,1

K:=K+S

i>6 K

i:=i+1

а) Цикл с постусловием

б) Цикл с предусловием

Рис. 10. Виды циклических алгоритмов

Классическим примером циклического алгоритма служит алгоритм для вычисления степени числа Y=Xⁿ . Этот алгоритм может быть реализован на основе операции умножения. Табличное представление такого алгоритма, отражающего зависимость У от Х при изменении показателя степени n от 1 до 3, представлено в табл.3. В этой таблице показанны также реккурентные соотношения между У и Х, определяющие как на каждом шаге зависит значение У от значения Х и от значения У, вычисленного на предыдущем шаге.

Таблица 3.Реккурентные соотношения при вычислении Y=Xⁿ

n	Y	Реккурентные соотно-
		шения
1	Y[1]=X	Y=X

2	Y[2]=X*X или	Y=XX или Y=YX
	Y[2]=Y[1]*X
3	Y[3]=XXX или	Y=XXX или Y=Y*X
	Y[3]=Y[2]*X

Текстовая форма алгоритма

___________________

Начало

Присвоить Х = -15

ПОКА Х <= 15

	1.Вычислить	K:=K+1
	Y= SIN(X)
	Y:=Y*x
	2.Вывести
	Y,X

S:=S+Y

3.Вычислить X=X+1,5

КОНЕЦ

19
НАЧАЛО
Ввод x, N
S:=0	НАЧАЛО
Y:=x
K:=1	X:= -15

K<N	x<=15

	КОНЕЦ
	Y =sin (X)
	Вывод S
	Y, X
	КОНЕЦ
	X: =X+1,5

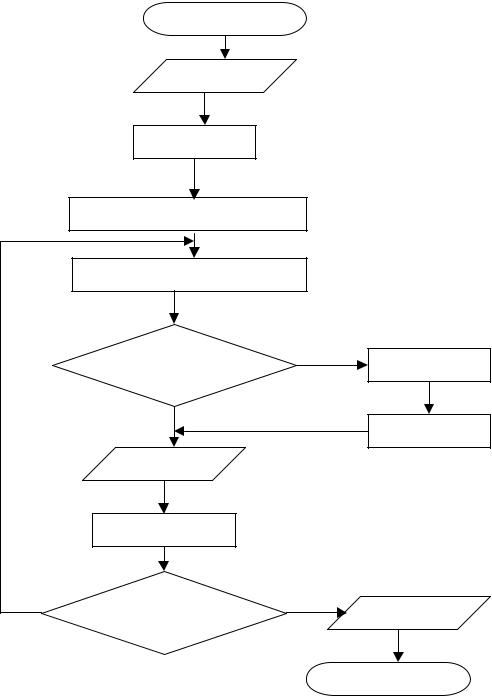
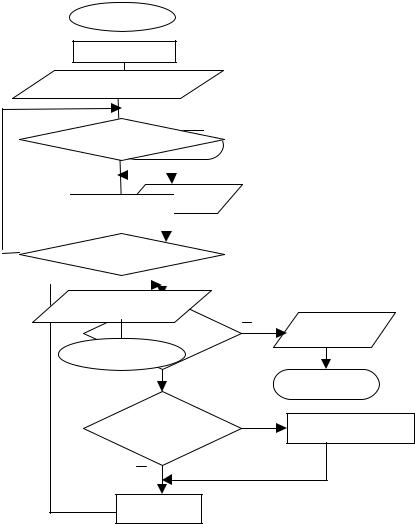
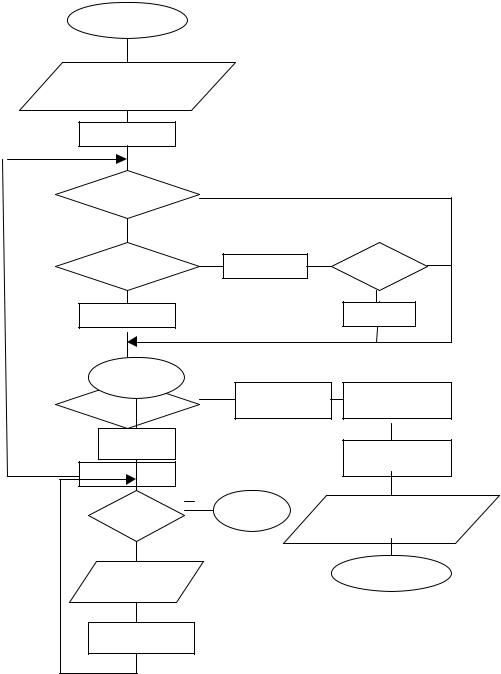
Рис.12. Алгоритм вычисления суммы ряда S=x+x^2+x^3+…+x^n

Пример 5.Пусть требуется составить алгоритм вычисления суммы ряда

S=x+x^2+x^3+…+x^n.

Решение. Исходные данные для алгоритма это переменные x и n. На каждом шаге будем вычислять очередной член суммы Y и прибавлять его к предыдущему значению суммы S.Для этого используем реккурентную формулу вычисления степени Х (см. таблицу 3) Y=Y*Х, тогда сумма ряда на каждом шаге итерации будет вычисляться по формуле S=S+Y. Количество итераций K изменяется от 1 до n и равно количеству членов ряда. Начальное значение суммы ряда S равно 0. На рис. 12 представлен циклический алгоритм с предусловием для вычисления заданной суммы ряда.

Пример 6. Требуется составить алгоритм получения на отрезке

[-15,15] множества значений функции Y= SIN(X) в виде таблицы значений (X,Y) при изменении аргумента Х по формуле X[k]=X[k-1]+h, где h=1,5.

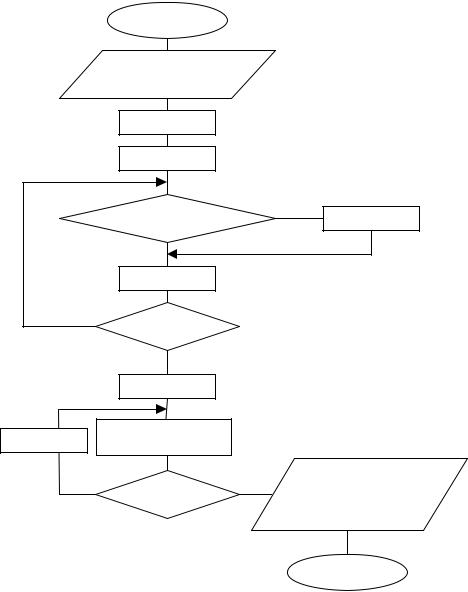
Решение. Такие задачи относят к задачам табулирования функций. Из условия задачи определяем, что начальное значение отрезка табулирования X= -15, конечное значение — X=15. Процесс получения множества пар Х,Y) является итерационным, значит проектируемый алгоритм будет циклическим. Условие выхода из цикла Х>15. На рис. 13 представлен циклический алгоритм с предусловием вычисления табличного значения функ-

ции Y= SIN(X) на отрезке -15<X<15 при изменении Х на каждом шаге итерации на величину 1,5. Результатом выполнения алгоритма является циклический вывод множеств пар

(Y,X) .

Рис. 13. Циклический алгоритм табулирования функции Y =sin (X)

Задания для самостоятельного выполнения

Составить визуальные циклические алгоритмы для следующих задач.

1.Вычислить число в факториале Y=X!

2.Вычислить сумму ряда , общий член которого задан формулой An=(x*n)/n!.

3.При табулировании функции y=cos(x+a) на отрезке [1,10] c шагом h=1 определить сумму значений y , больших p.

4.Подсчитать количество цифр в целом числе Х.

5.Вычислить сумму значений функции у=x^2 на отрезке [1,5] c шагом 1.

6.* Найти минимальное значение функции Y=Sin(X)*X , на отрезке [C,D] с шагом 0.001. Реализовать цикл с постусловием.

7.Протабулировать функцию y=sin(x) на отрезке [1,5] с шагом h=0,5. Вывести предпоследнее положительное значение функции.

8.Определить постановку задачи и составить визуальный алгоритм для этой задачи, если табличное представление ее решения изображено ниже:

Условие N>0	S	N
		0	125
125>0	да	0+5=5	12
12>0	да	5+2=7	1
1>0	да	7+1=8	0
0>0	нет

9.Составить визуальную и табличную формы алгоритма по его текстовому представлению, а также определить конечное значение S .

А) I=0; S=0;	В) I=1; S=0;
ПОКА I<3	ПОКА I >1
I=I+3	S=S+1/I
S=S+I*I	I=I-1
ВЫВОД S	ВЫВОД S

10. Составить визуальную и текстовую форму представления алгоритма, заданного в табличной форме.


		0
1	2	0+1+2=3
	3	3+1+3=7
2	2	7+2+2=11
	3	11+2+3=16

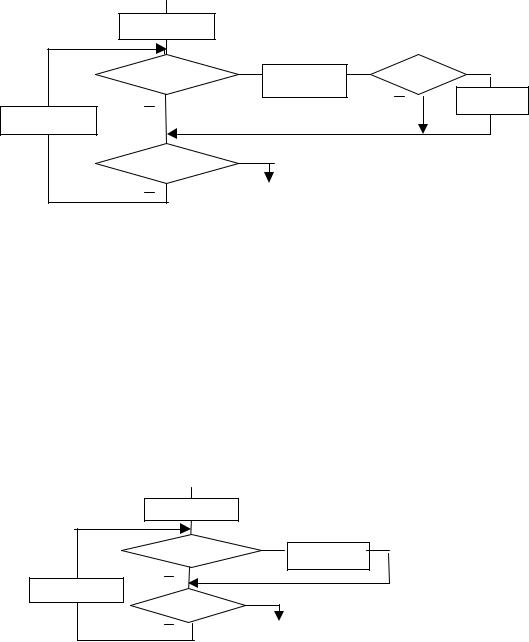
11.Определить является ли данный фрагмент алгоритма циклом, если да, то какого вида и какое действие является телом цикла?

A)	I=1	В)	I =1

	I<=6	+ +
	+
	K
	+
	K:=K+S	I := I +1

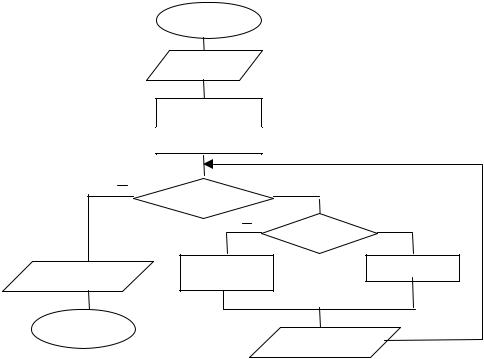
12.* Протабулировать функцию Y=tg(X), при изменении X на отрезке [A,B] с шагом K и определить количество точек разрыва(M) этой функции.

13.Определите местонахождение ошибок в алгоритмическом решении следующей задачи. Найти минимальное значение функции Y=A*X2+Sin(X)*X0,5 , для Х изменяющемся на отрезке [C,D] с шагом 0,01.

НАЧАЛО
C, D
X := C
M := AX2+SIN(X)X 0. 5
Y := AX2+SIN(X)X 0. 5
Y <M	Y=М

	C := Y
Y, X
X := X+0.001
X > D	M

	КОНЕЦ

8.АЛГОРИТМЫ ОБРАБОТКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ЧИСЕЛ

Последовательность значений — это набор однотипных величин, которые вводятся и обрабатываются циклически. Примером последовательности целых чисел может быть следующий набор значений: (2,5,-4,10,1,0). Последовательности значений отличаются от массивов значений тем, что в памяти одновременно все значения последовательности не хранятся. Для обозначения значения последовательности используют одну переменную, в которую на каждом шаге итерации вводится очередное значение последовательности. Отличительной особенностью последовательности является также возможность содержания неопределенного или неизвестного заранее количества ее значений. В этом случае критерием окончания последовательности служит некоторое особое значение, например, ноль.

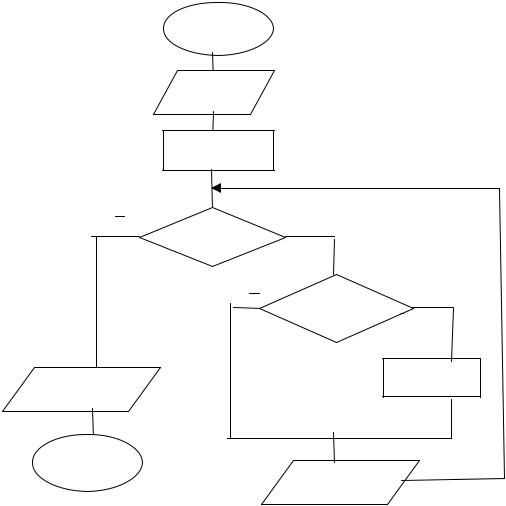
Пример 7. В числовой последовательности определить сумму положительных и произведение отрицательных чисел. Реализовать с помощью цикла с предусловием. Признак конца последовательности — значение 0. Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за S — сумму положительных значений , за Р — произведение отрицательных значений. Полученный алгоритм приведен на рис. 14. Условие

Рис.14. Алгоритм вычисления суммы положительных и произведения отрицательных значений числовой последовательности

для выбора вычислений Х>0. Для вычисления суммы значений воспользуемся реккурентной формулой S=S+X с начальным значением S=0, для вычисления произведения — реккурентной формулой P=P*X с начальным значением Р=1. Условие выхода из цикла неравенство Х<>0.

	НАЧАЛО
	Ввод X
	P:=1
	S:=0
	X<>0	+

		+
		X>0
Вывод P, S	P:=P*X	S:=S+X

КОНЕЦ

Ввод Х

Пример 8.Составить циклический алгоритм для определения в последовательности целых чисел количества четных чисел.

Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за K — количество четных значений (рис. 15). Условие для выбора четных значений Х mod 2=0 (остаток приделении Х

на 2 равен 0). Для вычисления количества значений воспользуемся реккурентной формулой К=К+1 с начальным значением К=0.

Рис. 15. Алгоритм определения количества четных чисел в последовательности значений

Задания для самостоятельного выполнения

Составить визуальные циклические алгоритмы для следующих задач обра-

НАЧАЛО

Ввод X

K=0

X<>0

K:=K+1

Вывод K

КОНЕЦ

Ввод Х

ботки последовательности значений.

1.В последовательности вещественных чисел подсчитать произведение чисел, кратных

2.В последовательности чисел сравнить ,что больше сумма положительных или произведение отрицательных.

3.В последовательности чисел определить предпоследнее отрицательное число.(При решении введите дополнительную переменную для хранения предпоследнего отрицательного числа).

4.В последовательности целых положительных чисел определить

максимальное число (Рекомендуем реализовать такой алгоритм :

			25
Вводим Х			mах=Х

Начало			Цикл с постусловием
		а. Если элемент Х > max
					то max:=Х (значение этого элемента);
			б. Вводим новый элемент последовательности Х.
K=1			Условие выхода из цикла Х=0 )
	5.	В последовательности целых чисел определить

			третье положительное число и подсчитать ко-
	Конец		личество цифр в нем.
K<=9
Ввод А(к)	9.АЛГОРИТМЫ ОБРАБОТКИ
ОДНОМЕРНЫХ ЧИСЛОВЫХ

		МАССИВОВ
К=К+1
			Под структурой данных типа массив
		понимают	однородную структуру	одно-
Рис. 16.Алгоритм ввода элементов	типных	данных, одновременно хранящихся
		в	последовательных ячейках оперативной
		памяти. Эта структура должна иметь имя и
определять заданное количество данных (элементов). Однотипность данных
определяет возможность использования циклических алгоритмов для	обра-
ботки всех элементов массива.	Количество итераций цикла определяется
количеством элементов массива Одновременное хранение в памяти всех эле-
ментов массива позволяет решать	большой	набор задач, таких как поиск
элементов, упорядочение и изменение порядка следования элементов.
Доступ	к любому элементу массива осуществляется по его номеру (
индексу ). Поэтому для обращения	к	элементу массива используют
имя_массива(номер элемента), например, А(5).
Массив называется одномерным , если для получения доступа к его
элементам достаточно одной индексной переменной.
Рассмотрим простой алгоритм ввода элементов одномерного числового
массива A из 9 элементов. В этом циклическом алгоритме условие выхода из
цикла определяется значением специальной
переменной К, которая называется	счетчиком элементов массива А
(рис.16), эта же переменная К определяет количество итераций циклического
алгоритма ввода элементов массива. На каждом шаге итерации переменная
К(значение номера элемента массива А) изменяется на 1, то есть происходит
переход к новому элементу массива.В дальнейшем, при рассмотрении
алгоритмов обработки одномерных массивов в целях устранения дублирова-
ния алгоритм ввода элементов массива будем заменять одним блоком,	под-
разумевая, что он реализуется по схеме, циклического алгоритма, представ-
ленного на ри-					сунке 16.

Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.

Решение. Алгоритм представлен на рисунке 17. В этом алгоритме переменная К — является счетчиком элементов массива, S — сумма элементов массива, она вычисляется по реккурентной формуле S=S+A(K). Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по схеме алгоритма ввода элементов массива, изображенного на рис.16.

Часто для проверки правильности работы алгоритмов на конкретных наборах данных используют таблицу трассировки. Эта таблица содержит столько столбцов, сколько переменных и условий в алгоритме, в ней мы вы-

полняем действия шаг за шагом от начала до конца алгоритма для конкретных наборов входных данных.НАЧАЛО

Пример 10. Составить алгоритм поиска

элемента

с максимальным значением в

одномерном массиве А(1..n) и его таблицу трассировки

для значений (3, 7, 0, 9).

Решение.

Введем обозначения K- текущий номер элемента, A[K] — текущее значение элемента массива,

Ввод N и А( 1.. N)

N=4 количество элементов одномерного массива, M- номер максимального элемента массива, A[M] — зна-

чение максимального элемента массива. Основной идеей

алгоритма

является выполнение сравнения теку-

A[М],

щего элемента массива A[K] и элемента с максимальным значением

определенным на предыдущем

A [K]>A[M]

шаге итерации.

По алгоритму

НАЧАЛО

изображенному

на рис.18

по-

лучено

максимальное значе-

ние для массива

(3, 7, 0,

9),

A(N)

процесс

и правильный резуль-

тат поиска которого показаны в

таблице 4.

K<=N K := 1

	Вывод А[M]
	K <= N	Вывод S
	КОНЕЦ
	+	КОНЕЦ

	A(K) > 0	+
	S := S+A(k)

K := K + 1

Рис. 17. Алгоритм вычисления суммы положительных элементов

Рис.18. Алгоритм поиска максимального значения в массиве

Таблица 4. Таблица трассировки алгоритма примера 10.

Номер элемен-	Значение эле-	Номер	макси-	Значение	мак-	Проверка
та массива К	мента А (К)	мального М	симальнго А(М)	А(К)>А(М)
1	3	1		3			Нет
2	7	1	2	3		7	да
3	0	2		7			нет
4	9	2	4	7		9	да

Рассмотрим несколько более сложных алгоритмов, в которых осуществляется изменение порядка следования элементов в одномерном массиве . К таким алгоритмам относят алгоритмы с перестановкой элементов местами, алгоритмы удаления некоторых элементов или циклического переноса некоторых элементов в начало или конец массива.

Основным требованием при составлении алгоритмов обработки массивов является неиспользование дополнительных массивов.

Чтобы точнее уяснить постановку задачи следует сначала рассмотреть частные решения для конкретных наборов входных данных (провести анализ) , затем обобщить полученное решение и определить набор решаемых задач. Составив визуальный алгоритм, его следует проверить на различных наборах исходных данных. Эти наборы исходных данных требуется подбирать таким образом, чтобы при заполнении таблиц трассировок проверить все пути вычислений данного алгоритма от начальной вершины до конечной.

Пример 11.Составить алгоритм решения и таблицу трассировки следующей задачи. В одномерном массиве поменять местами 2-ой нулевой элемент и последний положительный элемент. Применить нисходящее проектирование алгоритма.

Решение. Пусть одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0). Среди этих элементов имеются три нулевых значения, отрицательные и положительные значения. Второй нулевой элемент имеет порядковый номер 6, а последний положительный элемент — номер 3, его значение равно 4. Если поменять местами 2-ой нулевой элемент и последний положительный в исходном массиве (5, 0, 4, -3, -7, 0, -2, -4, 0)

то получим новый массив, в котором изменен порядок следования элементов 5, 0, 0, -3, -7, 4, -2, -4, 0 . Основными операциями алгоритма будут: поиск второго нулевого элемента массива, поиск по-

следнего положительного элемента массива и перестановка найденных элементов. Отметим, что для пере-

НАЧАЛО


			Перестановка эле-
Ввод мас-		ментов в массиве
Определение номера
сива
последнего

	элемента >0

Вывод Определение номера массива второго нулевого

элемента

КОНЕЦ

становки элементов необходимо знать номера переставляемых элементов. На рис. 19 изображен обобщенный алгоритм решения задачи, который в дальнейшем будет детализирован.

Рис. 19. Обобщенный алгоритм к примеру 11

Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по схеме алгоритма ввода элементов массива, изображенного на рис.16.

Поиск второго нулевого элемента массива будем осуществлять в цикле, проверяя значение очередного элемента на 0. Если очередной элемент равен 0, то для подсчета количества таких элементов используем реккурентную формулу M=M+1. В тот момент времени, когда значение М=2, нам необходимо запомнить номер текущего элемента массива, так как это и есть искомый второй положительный элемент исходного массива. На рис.20 приведен фрагмент алгоритма, реализующего поиск второго нулевого элемента в некотором массиве А из N элементов.

Рис. 20. Фрагмент алгоритма поиска второго нулевого элемента в массиве А, состоящем из N элементов. Здесь К- номер очередного элемента, А(К) — значение

K:=1 , m=0
A [K]=0	+	m=2
m:=m+1

P:=K

K:=K+1

K=N

очередного элемента, m -количество нулевых элементов, Р- номер второго нулевого элемента в массиве

Поиск последнего положительного элемента массива будем осуществлять аналогично в цикле, запоминая номер очередного элемента, значение которого больше нуля, в дополнительной переменной S. Учитывая тот факт, что после того как будут просмотрены и проверены на положительность все элементы массива в переменной S будет храниться номер последнего положительного элемента массива. На рис. 21 представлен фрагмент алгоритма поиска последнего положительного элемента в массиве А.

Рис. 21. Фрагмент алгоритма поиска последнего положительного элемента

Рассмотрим фрагменты алгоритма, приведенные на рис. 20 и 21. Можно заметить, что оба этих фрагмента выполняют поиск под управлением цикла, с одинаковым числом повторений, равным количеству элементов исходного массива N. Поэтому в итоговом алгоритме решения задачи примера 11 вместо композиции этих двух фрагментов в виде двух последовательных циклов можно использовать параллельное выполнение операций поиска под управлением одного цикла, который приведен на рис. 22.

S=K

K:=K+1

Рис 22. Алгоритм поиска второго нулевого и последнего положительного элементов массива А.

НАЧАЛО
Ввод N и элемен-
Q: =A [P]	A [P]: =A [S]
тов А(1.. N)
K:=1, m=0	A [S]: =Q

	+
A [K]<0
A [K]=0	+	m=2
m:=m+1
		+
S:=K		P:=K
K=N	+

	Перестановка
K:=K+1	элементов массива

	Вывод нового
	массива A[1..N]

КОНЕЦ

Напомним, что исходный одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0).По условию задачи необходимо поменять местами 2-ой нулевой элемент и последний положительный элемент.

Так как задачи поиска необходимых для перестановки элементов алгоритмически решены (рис. 22), то рассмотрим задачу перестановки элементовДля реализации перестановки найденных элементов достаточно воспользоваться управляющей структурой следования. Для того, чтобы во время перестановки не потерять переставляемые значения используем дополнительную переменную Q, временно хранящую одно из переставляемых значений элемента массива, в частности второе нулевое значение.На рис. 23 представлен универсальный алгоритм перестановки двух элементов одномерного массива, имеющих порядковые номера P и

S .

Рис. 23.Фрагмент перестановки двух элементов массива, с номерами S и P

Подводя итог для алгоритмического решения примера 11, приведем на рис. 24 алгоритм для вывода элементов преобразованного массива после перестановки найденных элементов.

Рис. 24. Алгоритм вывода элементов массива

Таким образом, процесс проектирование первоначального алгоритма перестановки второго нулевого элемента и последнего положительного элемента в одномерном массиве завершен. Полученный алгоритм представлен на рис.25. Следует заметить, что целью решения примера 11 было показать процесс нисходящего проектирования алгоритма » сверху-вниз » с использованием декомпозиции и метода структурной алгоритмизации. Отметим, что с целью упрощения в полученном алгоритме не рассматриваются ситуации, когда в составе элементов массива отсутствуют положительные значения или нулевые значения в количестве большем одного.

НАЧАЛО
Ввод N и элемен-
тов А(1.. N)
K=1, m=0
A [K]<0
A [K]=0	m:=m+1	m=2
S:=K		P:=K
Начало
	Q: =A [P]	A [P]: =A [S]
K=1		A [S]: =Q

K:=K+1
K<=9	Конец	Вывод нового
		массива A[1..N]
+
Вывод		КОНЕЦ
А к
К=К+1

Рис.25. Алгоритм перестановки второго нулевого и последнего положительного элемента в одномерном массиве

Для проверки правильности работы полученного алгоритма составим таблицу трассировки для одномерного массива из 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0), приведенных в примере 11. Напомним, что заполнение таблицы происходит по строкам. Считаем, что все начальные значения числовых переменных равны 0. В таблице 5 выполнена трассировка фрагмента поиска второго нулевого и последнего положительного элементов (их номеров), а в таблице 6 выполнена трассировка следующего фрагмента алгоритма по перестановке в массиве найденных элементов, где K- текущий номер элемента, A[K] — текущее значение элемента массива, М- количество нулей, обнаруженных в массиве при анализе очередного элемента, P- номер второго нулевого элемента массива, S- номер последнего положительного элемента массива, A[S] — значение последнего положительного элемента массива, A[P] — значение второго нулевого элемента массива.

Таблица 5.Таблица трассировки операций	Таблица 6. Таблица трассировки
поиска второго нулевого элемента и	перестановки найденных элемен-
последнего положительного	тов массива

К	Входной мас-	M	М=2	Р	S
	сив А(К)
1	5	0	Нет		1
2	0	1	Нет
3	4				3
4	-3
5	-7
6	0	2	Да	6
7	-2
8	-4
9	0	3	Нет

A(P)	Q	А(S)	Выходной мас-
А(6)		А(3)	сив А(К)
0	0	4	1	5
4	0	4	2	0
4	0	0	3	0
			4	-3
			5	-7
			6	4
			7	-2
			8	-4
			9	0

Пример 12. Составить алгоритм удаления в одномерном массиве элемента с максимальным значением. Решение. Анализ постановки задачи позволяет выделить две последовательно решаемые задачи: поиск элемента с максимальным значением и удаление этого значения из массива. Алгоритм первой задачи был рассмотрен ранее в примере 10 (рис.18). В этом алгоритме был определен номер максимального значения М, а максимальное значение определялось как А(М). Удаление элемента из массива приводит к уменьшению количества элементов массива за счет их перемещения на позицию удаляемого. Например, требуется удалить максимальное значение в массиве (2,4,13,5,7). Максимальное значение в этом примере равно 13. После удаления количество элементов данного массива уменьшится на 1 и станет равным 4, а массив примет вид (2,4,5,7). Таким образом, можно сделать вывод , что для удаления элемента из массива необходимо знать его номер, например М, удаление производится путем сдвига на одну позицию влево всех следующих за удаляемым элементов А(М)=А(М+1), этот сдвиг должен осуществляться под управлением цикла. Цикл завершит свою работу, когда последний элемент массива сдвинется на место предпоследнего элемента .

После приведенных рассуждений и используя алгоритмическое решение примера 10, изображенное на рис.18, составим алгоритм удаления элемента с максимальным значением из одномерного массива из N элементов (см. рис.26).

Рис. 26. Алгоритм удаления элемента с максимальным значением

К — номер очередного элемента, М- номер элемента с максимальным значением, N-1 — уменьшенное

НАЧАЛО
Ввод N и элемен-
тов А(1.. N)
А
K:=1
M:=1
A [K]>A [M]	M:=K
K:=K+1
K>N
K=М
A [K]: =A [K+1]
K:=K+1
	Вывод N-1 элемента
K=N-1	массива A

КОНЕЦ

в результате удаления одного элемента количество элементов массива А, A [K]: =A [K+1] — удаление путем сдвига влево следующих за удаляемым элементов на одну позицию.

Задания для самостоятельного выполнения

Составить визуальные циклические алгоритмы и таблицы трассировки для следующих задач обработки одномерных массивов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

План урока:

Понятие циклического алгоритма

Программирование циклического алгоритма

Операторы цикла

Решение задач с использованием операторов while, repeat, for

Понятие циклического алгоритма

В жизни людей очень часто встречаются циклы. Будь то жизнь маленького ребёнка или взрослого человека, а то и пожилых людей. Эти циклы можно расписать как выполнение одних и тех же действий, пока выполняется определённое условие. К примеру, взрослый человек находится на работе до момента, когда наступит время его ухода. И так изо дня в день, однако, есть и исключения в виде выходных. В жизни детей можно привести такой пример, как обязанность каждый день ходить в школу до момента, когда наступят выходные или каникулы.

Циклические алгоритмы – это алгоритмы, в которых некоторая часть операций повторяется многократно.

Цикл – конструкция с оператором, который повторяется определённое или неопределённое заранее количество раз. Действия, выполняющиеся последовательно внутри цикла, называют телом цикла.

В разных средах программирования циклические конструкции могут быть реализованы по-разному, но неизменным остается главный признак, отличающий циклы от линейных операций и ветвлений – возможность перемещения по программе не только «сверху-вниз», но и «снизу-вверх», для возврата к уже выполненным ранее действиям.

Циклы разделяют на три типа в зависимости от метода организации повторений:

Цикл, в котором задано условие окончания работы;
Когда известно условие продолжения работы цикла;
Когда известно число повторений цикла.

Программирование циклического алгоритма

Выбрав среду программирования Паскаль необходимо познакомиться с операторами, с помощью которых можно разработать программу с циклом. Ими являются while, repeat, for. Оператор while был разобран ещё на прошлом уроке, однако забывать о нём нельзя.

Цикл с предусловием

Цикл с предусловием реализует циклический алгоритм, записанный на языке программирования, с использованием определённого условия, истинность которого проверяется перед каждой итерацией цикла. Выполнение цикла прекращается, когда условие становится ложным.

Цикл с постусловием

Цикл с постусловием – это алгоритм циклической структуры, в котором проверка условия продолжения осуществляется после выполнения тела цикла.

Тело цикла с постусловием всегда выполняется как минимум один раз, независимо от истинности или ложности условия. Это его ключевое отличие от цикла с предусловием.

Такие циклы удобны, когда в условии используется результат выполнения тела цикла. Например, если мы хотим найти в тексте слово «стоп», мы должны сначала прочитать очередное слово, и только потом проверить, является ли оно искомым или следует продолжить поиск.

Цикл с заданным числом повторений

Этот вид цикла вместо логического условия выполнения использует параметр (счетчик) – специальную переменную, которая на каждом шаге цикла получает очередное значение из определенного диапазона. Цикл повторяется до тех пор, пока не будут перебраны все элементы диапазона. Таким образом, определяя диапазон, мы определяем заранее заданное число повторений.

Операторы цикла

Для программирования циклических алгоритмов и корректного выполнения программ с их использованием, необходимо знать операторы цикла. Чаще всего, в языке Паскаль используют операторы цикла: for, repeat и while. Разберем их подробнее.

Оператор while

Оператор while используется, когда нужно создать цикл с предусловием. Его схема в циклическом алгоритме выглядит следующим образом:

Если переводить его дословно, то можно сказать, что он работает по принципу «пока <условие> выполнять действие <оператор 1>», а заканчивается при переходе программы на слово end. Перед выполнением операторов внутри цикла условие обязательно проверяется и уже дальше, в зависимости от его истинности, программа либо выполняет тело цикла, либо переходит к последующим операторам.

Решение задач с использованием оператора while

Для более чёткого понимания решения задач нужно разобрать циклические алгоритмы, примеры которых приведены в решениях.

Задача 1. На вход подаются целые числа. До тех пор, пока не будет введено число, которое больше 17, программа должна вывести сумму полученного числа и числа 8. Когда вводимое число будет больше 17, то после выполнения программы цикл завершается.

Решение.

Шаг 1. Для начала необходимо дать программе название.

Шаг 2. Учитывая, что на вход подаётся целое число, указать тип данных, в данном случае – integer.

Шаг 3. Запись командного блока. Нужно написать слово, обозначающее начало, begin.

Шаг 4. Нужно дать переменной a значение 1, чтобы цикл начался автоматически.

Шаг 5. Запись цикла. Поскольку известно условие окончания работы, для этой задачи необходимо написать «пока a меньше или равно 17» и сделать переход к последующим операторам путём написания составного цикла.

Шаг 6. Первоначальный вывод программы. Необходимо написать то, что программа будет выдавать в первую очередь. В данном случае, она будет запрашивать целое число, запрос так и пишется: «Введите целое число: » .

Шаг 7. Запись необходимых операторов. Используя оператор readln программа считывает данные и переводит курсор на новую строку. Далее она производит операции над поступившими данными.

Шаг 8. Запись суммы. Исходя из условия задачи необходимо сделать так, чтобы программа выводила сумму входящего числа и числа 8. Осуществить это можно используя оператор writeln.

Шаг 9. Запись вывода программы после цикла. После того, как программа выполнит свою работу в цикле, необходимо показать, что она из него вышла. Можно просто попрощаться, как в данном случае.

Шаг 10. Проверка правильности записи алгоритма. В конце программного блока, после слова end нельзя забывать точку, её обязательно нужно поставить.

Оператор repeat

Оператор цикла repeat until используется для создания циклического алгоритма с постусловием. Его схема выглядит так:

Дословно оператор Паскаля repeat можно перевести как «повторяй <оператор 1>, до <условие>». В зависимости от истинности условия, либо происходит переход на повторение «оператора 1», либо осуществляется выход из цикла к последующим операторам.

Оператор repeat имеет два важных отличия от оператора while:

в операторе repeat сначала выполняется тело, а затем проверяется условие;
в операторе repeat прописывается условие завершения цикла, тогда как в операторе while – условие его продолжения.

Решение задач с использованием оператора repeat

Задача 1. Придумать алгоритм и написать по нему программу, результатом выполнения которой будет вывод последовательности натуральных чисел от 1 до введенного пользователем числа.

Решение.

Шаг 1. Название программы. В данном случае — «задача 1».

Шаг 2. Учитывая, что на вход подаются целые числа, требуется указать тип данных – integer.

Шаг 3. Командный блок. Запись начального слова begin.

Шаг 4. Вывод запроса программы. Поскольку программе необходимо целое число, нужно попросить пользователя ввести его. Осуществляется это с помощью процедуры writeln и текста «Введите целое число, которое больше 1: ».

Шаг 5. Необходимо присвоить переменной i значение 1 для того, чтобы последовательность начиналась с натурального числа.

Шаг 6. Запись цикла. Учитывая, что используется цикл с постусловием, необходимо сначала записать оператор, который будет повторяться, затем увеличить i на 1, чтобы образовывалась последовательность, и уже после этого прописать условие повторения. В данной задаче цикл перестаёт повторяться тогда, когда переменная i принимает значение больше введённого числа, которое является последним членом последовательности.

Шаг 7. Проверка программы на правильность в выводе. В результате своей работы программа должна вывести последовательность натуральных чисел от 1 до n, через пробел.

Оператор for

Используя оператор for можно задать нужное количество повторений одних и тех же действий. По-другому его называют оператором циклов с известным числом повторений. Он имеет два соединительных слова – это to и downto. Различие между ними в том, что при использовании первого к предыдущему значению переменной цикла прибавляется единица, а при написании второго – вычитается единица. Схемы оператора имеют следующий вид:

Дословно его можно перевести как «для переменной в значении от начального к конечному выполнять <оператор 1> ».

Решение задач с использованием оператора for

Рассмотреть пример с оператором for можно при написании короткого алгоритма для следующей задачи.

Задача 1. Напишите на одном из языков программирование алгоритм, который выводит квадраты чисел от 1 до 10.

Решение.

Шаг 1. Необходимо дать программе название.

Шаг 2. Поскольку на вход числа не подаются, тип указывается в зависимости от данных, которые изначально находятся в программе. В данном случае – это целые числа.

Шаг 3. Запись блока с командами алгоритма.

Шаг 4. Перебор последовательности чисел осуществляется в цикле for, в котором счетчик i пробегает значения от 1 до 10, а расчет и вывод квадратов осуществляется в процедуре write.

Решение задач с использованием операторов while, repeat, for

Задача 1 Разработать алгоритм программы, которая выведет таблицу умножения чисел от 1 до 10 на 9.

Решение

Для решения можно написать два вида кода. Однако, этапы разработки программы, задачи, которые ей необходимо выполнить, очень похожи на прошлые примеры, и она ничем не отличается от решения обычной задачи. Поскольку различие в этих двух кодах лишь в использованном операторе while и for, то рассматривать их по-отдельности нет смысла. Последовательность написания первого кода выглядит так:

Шаг 1. Нужно назвать программу.

Шаг 2. Так как пользователь не вводит никаких данных, то их можно ввести в сам код программы. Тип используемых данных в данном случае – это integer.

Шаг 3. Написание команд. Изначально нужно сделать так, чтобы программа вывела название того, для чего она предназначена. В данной задаче это «Таблица умножения на 9».

Шаг 4. Запись цикла for. С помощью него программа будет последовательно умножать числа от 1 до 10 на 9 и составлять таблицу умножения путём вывода каждого значения по схеме «9x, i, =, p», где i – умножаемое на 9 число, p – результат произведения 9 и i.

Шаг 6. Программа завершает свою работу. Необходимо проверить правильность выведенных данных и, если это необходимо, поправить код для более корректной работы.

Источник

to continue to Google Sites

Not your computer? Use Guest mode to sign in privately. Learn more

Источник

Циклическим называется алгоритм, в котором серия команд выполняется определённое количество раз.

Циклы бывают: с параметром (счётчиком), с условием. Циклы с условием ещё называют итерационными.

Циклы с параметром (счётчиком) выполняются заданное число раз.

Программа на Pascal	Программа на Python
for (i)(:) (= n) to (k) do begin … end;	for (i) in range((n)): …

Пример

Дан ряд чисел от (1) до (20), нужно найти сумму ряда.

Чтобы найти сумму, нужно выполнить алгоритм (20) раз. Обозначим слагаемое через (i) и на каждом повторе будем добавлять в переменную (S). Запишем программу.

Рис. (1). Программа на Pascal

Рис. (2). Программа на Python

Примечание: в программном коде на Python в строке for i in range указываем (21), т. к. последнее число в заданный диапазон не входит.

Добавим в программу условие, например: нужно сложить не все цифры диапазона, а только чётные. Условие проверяет чётность числа.

Рис. (3). Программа на Pascal

Рис. (4). Программа на Python

Усложним условие: дан ряд из (N) чисел, посчитать количество чисел, кратных (5) и не кратных (3).

Рис. (5). Программа на Pascal

Рис. (6). Программа на Python

Циклы с условием

В Pascal используются циклы с постусловием (repeat… until) и предусловием (while), а в Python используется только while.

В чём отличие?

Цикл repeat… until — цикл, в котором серия команд повторяется, пока не выполнено условие, а в цикле while серия команд выполняется, пока выполняется условие.
В цикле while серия команд может не выполниться ни разу, в цикле repeat такого произойти не может — хоть раз, но выполнится.
В Python нет цикла repeat, но его можно организовать с помощью цикла while, например так:

Рис. (7). Программа с использованием постусловия

While True будет выполняться бесконечно, но при вводе с клавиатуры числа больше (0) цикл закончится.

Рассмотрим задачу: определить количество чётных цифр в числе.

Составим алгоритм решения задачи.

1. Вводим число.
2. «Отсекаем» последнюю цифру числа ((a)(:) (= x) (mod) (10)).
3. Проверяем: если цифра чётная ((if) (a) (mod) (2 = 0) (then) (k)(:) (= k + 1)), то добавляем в переменную, например (k), единицу ((k)(:) (= k + 1)).
4. Уменьшаем количество цифр на одну, команда (x) (div) (10) уменьшает число на (1) разряд.
5. Повторяем цикл, пока есть цифры в числе (while (x > 0) (do)).

Рис. (8). Программа на Pascal

Рис. (9). Программа на Python

Решение задачи «Как на ЕГЭ» № (17)

Рассматривается множество целых чисел, принадлежащих полуинтервалу ((1310; 13154]), которые делятся на (3) и не делятся на (9, 11, 19).

Найди количество таких чисел и разницу между максимальным и минимальным числом.

Составим алгоритм решения.

1. Для решения будем использовать цикл for, диапазон от (1311) (круглая скобка) до (13154) включительно.
2. С помощью определения остатка от деления находим количество чисел, кратных (3) и не кратных (9), (11), (19).
3. Найдём максимальное число, которое попадает под условие (максимальным будет число, которое попадает под условие позже всего).
4. Найдём минимальное число, которое попадает под условие (минимальное число можно найти, «прокрутив» последовательность в обратном порядке).
5. Найдём разницу между минимальным и максимальным числом.

Рис. (10). Программа на Pascal

Ответ:

(k = 2265).

Разница max-min (= 11835).

Рис. (11). Программа на Python

Ответ:

(k = 2265).

Разница max-min (= 11835).

Как на ЕГЭ. Задание № (14).

Для решения задания рассмотрим программу на Python.

Алгоритм решения.

1. Запишем число в переменную, например (x).

2. Организуем цикл while, пока (x) больше (0), будем выполнять следующие действия:

определим остаток от деления (x) на основание системы счисления (например, (2)).
Если будем считать количество единиц в числе, то добавим в переменную, например (k), единицу.
Уменьшим число, т. е. поделим нацело на (2).

3. Напечатаем (k).

Значение арифметического выражения:

42018+8512−22017−130

записали в системе счисления с основанием (2). Сколько значащих нулей содержится в этой записи?

Рис. (12). Программа на Python

Ответ: (483).

Источники:

Источник

Практическая работа № 6.

Тема: Программная реализация циклического алгоритма.

Цель: Научиться программировать циклические алгоритмы.

Оборудование: ПК, система программирования Qbasic.

Ход работы

1. Изучить основные сведения по теме.

Основные сведения

При решении некоторых задач требуется выполнять одни и те же действия несколько раз. Такая последовательность команд называется циклом.

Организация цикла в программе:

FOR I=L TO K STEP H

тело цикла

NEXT I

I – счетчик цикла,

L – начальное значение счетчика,

К – конечное значение счетчика,

H – шаг (величина, прибавляемая к значению счетчика). Если шаг не указан, он считается равным 1.

Тело цикла – набор операторов, предназначенных для повторения.

2. Запишите в тетрадь примеры решения задач. Запустите программу qbasic2. Введите программы из примеров. Запустите на выполнение (RUN-Start или F5), запишите в тетрадь ответы. Сохраните программы на диске Х: под именем lr4pr1.bas, lr4pr2.bas и т.д.

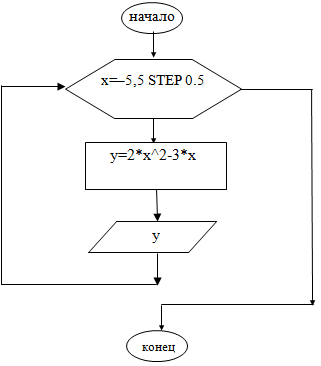
Пример 1. Найти значения функции y=2x²-3x на отрезке [-5;5] с шагом 0,5

Блок схема:

Программа:

10 REM znachenie funkcii

20 CLS

30 FOR x= -5 TO 5 STEP 0.5

40 LET y=2*x^2-3*x

50 PRINT “y(”; x; “)=”; y

60 NEXT x

70 END

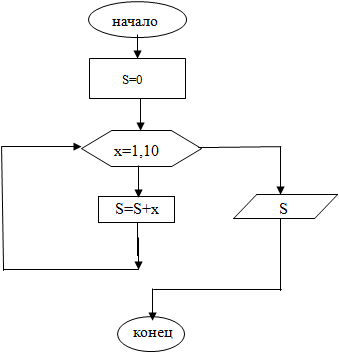
Пример 2. Найти сумму целых чисел от 1до 10.

Блок схема:

Программа:

10 REM Summa ot 1 do 10

20 CLS

30 LET S=0

40 FOR x=1 TO 10

50 LET S=S+x

60 NEXT x

70 PRINT “Summa S=”; S

80 END

3. Составить блок-схему и программу для решения задач по теме. Ввести программу в компьютер, отладить ее, получить результат.

ЗАДАЧИ

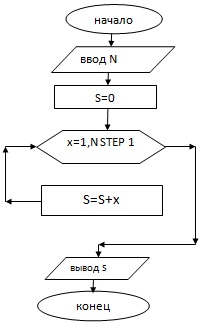
1.Найти сумму натуральных чисел до n.

Блок-схема:

10 REM summa naturalnyh chisel

20 CLS

30 INPUT “vvedite N” ; N

40 LET S=0

50 FOR x=1 TO N STEP 1

60 LET S=S+x

70 NEXT x

80 PRINT “summa naturalnyh chisel S=” ; S

90 END

Ответ: 1)N=9 summa naturalnyh chisel S=45

2)N= summa naturalnyh chisel S=

3)N= summa naturalnyh chisel S=

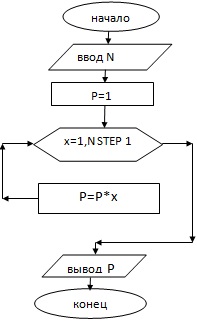
2.Найти произведение натуральных чисел до n.

Блок-схема:

10 REM proizvedenie naturalnyh chisel

20 CLS

30 INPUT “vvedite N” ; N

40 LET P=1

50 FOR x=1 TO N STEP 1

60 LET P=P*x

70 NEXT x

80 PRINT “proizvedenie naturalnyh chisel P=” ; P

90 END

Ответ: 1)N= proizvedenie naturalnyh chisel P =

2)N= proizvedenie naturalnyh chisel P =

3)N= proizvedenie naturalnyh chisel P =

3.Найти значение функции y=x³+3cosx в интервале от 0 до 5 с шагом 1.

4.Напечатать квадраты чисел от 1 до 10.

5.Посчитать произведение целых чисел от 3 до к.

6.Посчитать сумму чисел от 0 до р с шагом 0,5

7.Посчитать сумму чисел от 0 до n с шагом h.

8.Посчитать сумму 1+1/2+1/3+…+1/n.

9.Посчитать произведение 1*1/2*1/3*…*1/k.

10.Найти 2ⁿ, d – целое положительное число.

11.Дано натуральное число. Найти все его натуральные делители.

12. Запросить число, вывести таблицу умножения для него.

5.Работа над контрольными вопросами.

Контрольные вопросы

Что такое цикл в программе?
Перечислите операторы, используемые при написании циклических программ?
Как на языке Qbasic организовать цикл?
Каково назначение переменных I, L, K, H?
Можно ли не указывать шаг цикла?
Для чего предназначен оператор NEXT? Можно ли его не писать?

Презентация к уроку «Программная реализация циклического алгоритма.»

Расширения для Joomla

Источник