Как найти сумму векторов по правилу параллелограмма - Исправление недочетов и поиск решений вместе с Examum.ru

Сложение векторов по правилу параллелограмма

Даны векторы

a→

b→

. Если векторы

a→

b→

исходят из одной точки, то вектор суммы

c→

исходит из общей начальной точки векторов и является диагональю параллелограмма, сторонами которого являются векторы

a→

b→

Запись:

a→+b→=c→

или

AB→+AD→=AC→

Такой приём сложения векторов называется правилом параллелограмма.

Так как

DC→=AB→=b→

, то

a→+b→=AD→+DC→=AC→=c→

; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор

c→

. Поэтому оба способа сложения равноценны.

1. Для любых двух векторов

a→

b→

в силе равенство

a→+b→=b→+a→

(коммутативный, или переместительный, закон сложения).

2. Для любых трёх векторов

a→

b→

c→

в силе равенство

a→+b→+c→=a→+b→+c→

(ассоциативный, или сочетательный, закон сложения).

Источник

Сложение
и вычитание векторов.

Сумма
двух векторов. Законы сложения векторов. Правило параллелограмма.

Представим себе такую ситуацию.
Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в
магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой.
Сейчас мы описали принцип первого правила сложения векторов.

Правило треугольника.

Чтобы найти вектор суммы двух векторов и , нужно:

1) совместить параллельным переносом начало вектора с концом
вектора ;

2) провести вектор из начала вектора в конец
вектора ;

3) получившийся вектор и есть вектор суммы: .

Если к вектору прибавить
нулевой вектор по правилу
треугольника, то получим вектор , т.е.
справедливо равенство: .

Утверждение. Если и –
произвольные точки, то .

Например, .

Сложение векторов подчиняется алгебраическим законам.

ТЕОРЕМА.
Для любых векторов и справедливы
равенства:

(переместительный
закон)

(сочетательный
закон).

Дано:

Доказать: 1)

Доказательство.

Доказательство теоремы в случае, когда
векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно.
Мы рассмотрим случай, когда данные векторы неколлинеарны.

1). Отметим произвольную точку и отложим от этой точки
вектор . Воспользуемся правилом
треугольника и прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок слева).

Теперь от точки и отложим вектор . По правилу треугольника
прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок справа).

– параллелограмм и точка совпадает с точкой . Значит, , т.е.

2). От точки отложим вектор , от точки отложим вектор , а от точки – вектор . Найдём суммы векторов по
правилу треугольника.

Теорема доказана.

При доказательстве первой формулы получился параллелограмм,
причём, из точки выходят два вектора и , а вектор их суммы является
диагональю параллелограмма. На основе этого возникает второе правило
геометрического сложения векторов.

Правило параллелограмма.

Чтобы найти вектор суммы двух векторов и , нужно:

1) совместить параллельным переносом начала векторов и ;

2) на этих векторах достроить параллелограмм;

3) вектором суммы является
вектор, который лежит на диагонали параллелограмма, имеющий своё начало в
начале исходных векторов.

Сумма
нескольких векторов.

Сложение нескольких векторов происходит по принципу правила
треугольника. Складываются два вектора, к вектору суммы прибавляется следующий
вектор и т.д. Приведём пример.

Сложить векторы .

Отметим точку и отложим от неё вектор . Прибавим к нему вектор по правилу треугольника. . Теперь к вектору прибавим вектор . . К вектору прибавляем вектор . . Осталось к вектору прибавить вектор . .

Итак, . Значит, суммой векторов является вектор, с началом
в начале первого вектора и концом – в конце последнего. Такое сложение векторов
называется правилом многоугольника.

Правило многоугольника.

Чтобы найти вектор суммы нескольких векторов, нужно:

1) последовательно совместить параллельным переносом начало
последующего вектора с концом предыдущего;

2) вектором суммы всех векторов является вектор, с началом в
начале первого вектора и концом – в конце последнего.

Вычитание
векторов.

Определение. Разностью
двух векторов и называется такой вектор , что при
сложении его с вектором получается
вектор .

Вычитание
векторов можно производить, руководствуясь двумя понятиями: следствием из
правила треугольника сложения векторов; определением разности двух чисел. Разберём
каждое из них.

Сложим векторы и по правилу треугольника. По
рисунку видно, что . Отсюда, и . Значит, разность двух
векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда
два правила:

I правило
вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно:

1) совместить параллельным переносом начала этих векторов;

2) вектором разности является вектор с началом в конце второго вектора
и концом в конце первого вектора.

II правило
вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно:

1) совместить параллельным переносом концы этих векторов;

2) вектором разности является вектор с началом в начале первого
вектора и концом в начале второго вектора.

Далее, из алгебры мы знаем, что для того, чтобы
из числа вычесть
число , нужно к числу прибавить
число, противоположное числу , т.е. . Такое же
правило справедливо и для векторов.

ТЕОРЕМА.
Для любых векторов справедливо
равенство:

Дано:

Доказать:

Доказательство.

1. Найдём разность векторов по
I правилу. Вектором разности является
вектор (рисунок слева). А теперь
найдём сумму векторов по правилу
треугольника, где – вектор,
противоположный вектору . Вектором
суммы является вектор (рисунок
справа). Не трудно заметить, что . Они сонаправлены и имеют
одинаковые модули.

2. А теперь докажем то же самое аналитически. По определению
разности векторов,

Что и требовалось доказать.

Из этой теоремы следует третье правило
вычитания векторов.

III правило
вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный
второму.

Используя это правило вычитания векторов,
способ сложения векторов выбирается произвольно.

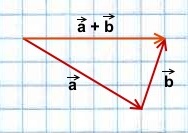
1. Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.

2. Проведите векторы . Какая геометрическая фигура у вас
получилась?

3. Вектор является разностью векторов и . Определите, какой из четырёх рисунков
верный.

4. Вектор является суммой векторов и . Определите, какой из четырёх рисунков
верный.

5. Выразите
вектор через векторы , используя рисунок.

6. Выразите
вектор через векторы , используя рисунок.

7. Упростите выражения:

8. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может
принимать длина вектора ?

9. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может
принимать длина вектора ?

10. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может
принимать длина вектора ?

11. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может
принимать длина вектора ?

12. Длина вектора равна , а длина вектора равна . Сколько различных целых значений может
принимать длина вектора ?

13. В квадрате проведены диагонали и . Укажите номера верных утверждений.

1)	2)	3)
4)	5)	6)
7)

14. – параллелограмм. Найдите сумму векторов .

15. – прямоугольник. Диагонали и пересекаются в точке . Укажите номера верных утверждений.

1)	2)	3)
4)	5)	6)
7)		9)	10)

16. – параллелограмм. Выразите векторы и через векторы и .

17. – параллелограмм. Выразите векторы и через векторы и .

18. – прямоугольник. Выразите векторы и через векторы и .

19. – параллелограмм. Выразите векторы и через векторы и .

20. Найдите длины
векторов , изображённых на клетчатой бумаге с
размерами клетки 1 х 1.

21. Две стороны
прямоугольника равны 20 и 21. Найдите длину суммы
векторов и .

22. Две стороны
прямоугольника равны 7 и 24. Найдите длину разности
векторов и .

23. На каждом рисунке
найдите длину вектора (размеры клетки 1 х 1).

24. На каждом рисунке
найдите длину суммы векторов и (размеры клетки 1 х 1).

25. На каждом рисунке
найдите длину разности векторов и , изображённых на клетчатой бумаге с
размерами клетки 1 х 1.

Источник

Определение

Сумма векторов

— это вектор

с координатами c₁=a₁+b₁, c₂=a₂+b₂, то есть

или

$[(overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 ;b_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Свойства сложения векторов:

Для любых векторов

верны свойства:

1) переместительное:

2) сочетательное:

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Доказательство:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

$[1)overrightarrow a (a_1 ;a_2 ) + overrightarrow b (b_1 ;b_2 ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ),]$

$[overrightarrow b (b_1 ;b_2 ) + overrightarrow a (a_1 ;a_2 ) = (overrightarrow {b_1 + a_1 ;b_2 + a_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Так как соответствующие координаты равны, то эти векторы равны.

Аналогично

$[2)overrightarrow a (a_1 ;a_2 ) + (overrightarrow b (overrightarrow {b_1 ;b_2 } ) + overrightarrow c (c_1 ;c_2 )) = ]$

$[= (overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 + c_1 ;b_2 + c_2 } ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } ),]$

$[(overrightarrow a (a_1 ;a_2 ) + overrightarrow b (overrightarrow {b_1 ;b_2 } )) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } );]$

$[3)overrightarrow a (a_1 ;a_2 ) + overrightarrow 0 (0;0) = (overrightarrow {a_1 + 0;a_2 + 0} ) = (overrightarrow {a_1 ;a_2 } ) = overrightarrow a .]$

Теорема

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Доказательство:

Для точек A (x₁;y₁), B (x₂;y₂), C (x₃;y₃)

$[overrightarrow {AB} (x_2 - x_1 ;y_2 - y_1 ),]$

$[overrightarrow {BC} (x_3 - x_2 ;y_3 - y_2 ),]$

$[overrightarrow {AC} (x_3 - x_1 ;y_3 - y_1 ).]$

Тогда

$[overrightarrow {AB} + overrightarrow {BC} = (overrightarrow {x_2 - x_1 + x_3 - x_2 ;y_2 - y_1 + y_3 - y_2 } ) = ]$

$[= (overrightarrow {x_3 - x_1 ;y_3 - y_1 } ) = overrightarrow {AC} .]$

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

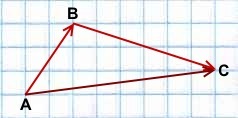
(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

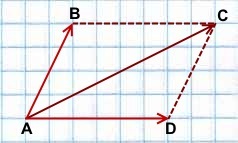
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Пример.

Построить сумму векторов

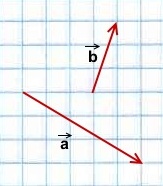
Решение:

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

вектор

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

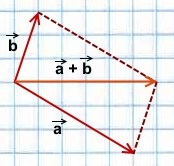
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

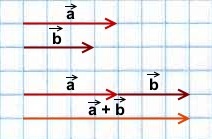
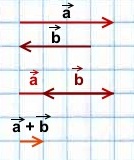
Сложение коллинеарных векторов

1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Источник

Часть математических и физических задач содержит необходимость математических действий с векторами (сложение и вычитание).

Проиллюстрируем сложение. Пусть даны вектора и , попытаемся найти вектор displaystyle vec{c}=vec{a}+vec{b} .

Способ 1. Метод сложения треугольником

Возьмём необходимые вектора и параллельным переносом совместим конец первого вектора () и начало второго ( displaystyle vec{b} ) (рис. 1)

Рис. 1. Сложение векторов (правило треугольника)

Тогда вектор, соединяющий начальную точку первого вектора () и конец второго (), является вектором ( displaystyle vec{c} ).

Способ 2. Метод сложения параллелограммом

Возьмём необходимые вектора и параллельным переносом совместим начало первого вектора () и начало второго ( displaystyle vec{b} ) (рис. 2). Параллельным переносом совместим конец каждого вектора с началом другого.

Рис. 2. Сложение векторов (правило параллелограмма)

Тогда вектор, соединяющий общую начальную точку первого () и второго () векторов и общий конец данных векторов, является вектором суммы ( displaystyle vec{c} ).

Вывод: в ряде задач, где присутствуют несколько однородных векторных физических величин, часто необходимо найти общий вектор (общую скорость, равнодействующую силу, полный вектор магнитной индукции или электрической напряжённости поля). Тогда необходимо сначала сложить вектора, а потом найти модуль получившегося вектора.Чаще всего первый метод используется в кинематике (сложение скоростей). Второй метод часто используют в динамике.

Источник

Содержание:

§ 1 Переместительный закон сложения векторов
§ 2 Сочетательный закон сложения векторов
§ 3 Сложение нескольких векторов
§ 4 Краткие итоги урока

§ 1 Переместительный закон сложения векторов

В алгебре часто при упрощении выражений и различных вычислениях используются переместительный и сочетательный законы.

Эти законы также справедливы для векторов.

Вспомним правило сложения векторов – правило треугольника.

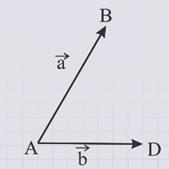
Пусть нам даны два вектора а и b.

От произвольно выбранной точки А отложим вектор АВ, равный вектору а.

Затем от точки В отложим вектор ВС, равный вектору b.

Вектор АС называется суммой векторов а и b.

Воспользуемся этим правилом треугольника для доказательства следующей теоремы.

Теорема:

Для любых векторов а , b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а (переместительный закон);

сумма векторов а плюс b и с равна сумме векторов а и b плюс с (сочетательный закон).

Для доказательства переместительного закона рассмотрим случай, когда векторы а и b не коллинеарны, т.е. ненулевые и не лежат на одной или параллельных прямых (случай коллинеарных векторов рассмотрите самостоятельно).

От произвольной точки А отложим вектор АВ, равный вектору а, и вектор АD, равный вектору b.

Основываясь на построенных векторах, достроим параллелограмм АВСD так, что вектор АВ равен вектору DС, а вектор АD равен вектору ВС.

По правилу треугольника сумма векторов АВ и ВС равна вектору АС, т.е. равна сумме векторов а и b.

С другой стороны, сумма векторов AD и DC также равна вектору АС, т.е. сумме векторов b и а.

Таким образом, сумма векторов а и b равна сумме векторов b и а.

Переместительный закон доказан.

§ 2 Сочетательный закон сложения векторов

Для доказательства сочетательного закона отложим от произвольной точки А вектор АВ, равный вектору а, от точки В вектор ВС, равный вектору b, и от точки С вектор CD, равный вектору с.

Рассмотрим сумму векторов а плюс b и вектора с с точки зрения правила треугольника: сумма векторов а и b равна вектору АС, в свою очередь, сумма вектора АС и вектора с равна вектору АD.

Теперь рассмотрим сумму векторов а и b плюс с: сумма векторов b и с, согласно рисунку, равна вектору ВD, в свою очередь, сумма векторов а и ВD равна вектору АD.

Исходя из этого, сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

Что доказывает сочетательный закон.

Теорема доказана.

Важно отметить, что при доказательстве переместительного закона было обосновано правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы а и b, необходимо от произвольной точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b.

§ 3 Сложение нескольких векторов

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов?

Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке происходит сложение.

Рассмотрим рисунок, отражающий сумму векторов а, b и с:

от произвольной точки А отложен вектор АВ, равный вектору а, затем от точки В отложен вектор ВС, равный вектору b, и, наконец, от точки С отложен вектор CD, равный вектору с.

В результате получается вектор АD, равный сумме векторов а, b и с.

Если продолжить процесс откладывания векторов, можно построить сумму четырех, пяти, любого количества векторов.

Правило построения суммы нескольких векторов называется правилом многоугольника: если А1, А2, …,Аn – произвольные точки плоскости, то сумма векторов А1А2, А2А3, …, Аn –1An равна вектору А1Аn.

Это равенство справедливо для всех точек А1, А2, …, Аn, в частности, когда некоторые из них совпадают.

Важно заметить, что если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.

§ 4 Краткие итоги урока

Итак, подведем итоги:

– Для любых векторов а, b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а;

сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

– Чтобы сложить неколлинеарные векторы а и b, необходимо от точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b (правило параллелограмма).

– Если А1, А2 … An – произвольные точки плоскости, то сумма векторов

А1А2, А2А3,.., Аn–1An равна вектору А1Аn (правило многоугольника).

Список использованной литературы:

Атанасян Л.С. Учебник: Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. –383 с.
Геометрия. Ч.I. Планиметрия: учебное пособие/ И.Б. Барский, Г.Н. Тимофеев. – Йошкар-Ола: изд-во Марийского гос. ун-та, 2006 и 2008. – 636с.

Источник