Как найти сумму векторов правило треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
Разность векторов
- Формула вычитания векторов
Примеры задач

Сумма векторов

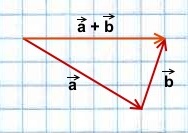
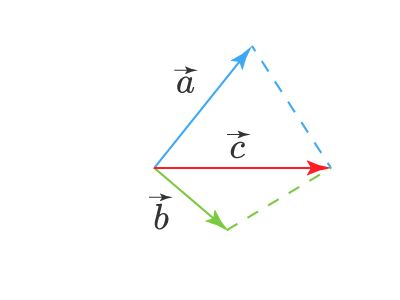
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c, начало которого совпадает с началом a, а конец – с концом b. При этом конец вектора a должен совпадать с началом вектора b.

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c, совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

c_i = a_i + b_i

Элементы вектора c равняются попарной сумме соответствующих элементов a и b.


Для плоских задач	a + b = {a_x + b_x; a_y + b_y}
Для трехмерных задач	a + b = {a_x + b_x; a_y + b_y; a_z + b_z}
Для n-мерных векторов	a + b = {a₁ + b₁; a₂ + b₂; … a_n + b_n}

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: (a + b) + c = a + (b + c)

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (-a) = 0

Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b, то получится c, причем должно соблюдаться условие: b + c = a

Формула вычитания векторов

c_i = a_i – b_i

Элементы вектора c равны попарной разности соответствующих элементов a и b.


Для плоских задач	a — b = {a_x — b_x; a_y — b_y}
Для трехмерных задач	a — b = {a_x — b_x; a_y — b_y; a_z — b_z}
Для n-мерных векторов	a — b = {a₁ — b₁; a₂ — b₂; … a_n — b_n}

Примеры задач

Задание 1
Вычислим сумму векторов a = {3; 5} и b = {2; 7}.

Решение:
a + b = {3 + 2; 5 + 7} = {5; 12}.

Задание 2
Найдем разность векторов a = {4; 8; -2} и b = {-1; 9; 5}.

Решение:
a – b = {4 – (-1); 8 – 9; -2 – 5} = {5; -1; -7}.

Источник

Определение

Сумма векторов

— это вектор

с координатами c₁=a₁+b₁, c₂=a₂+b₂, то есть

или

$[(overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 ;b_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Свойства сложения векторов:

Для любых векторов

верны свойства:

1) переместительное:

2) сочетательное:

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Доказательство:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

$[1)overrightarrow a (a_1 ;a_2 ) + overrightarrow b (b_1 ;b_2 ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ),]$

$[overrightarrow b (b_1 ;b_2 ) + overrightarrow a (a_1 ;a_2 ) = (overrightarrow {b_1 + a_1 ;b_2 + a_2 } ) = (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ).]$

Так как соответствующие координаты равны, то эти векторы равны.

Аналогично

$[2)overrightarrow a (a_1 ;a_2 ) + (overrightarrow b (overrightarrow {b_1 ;b_2 } ) + overrightarrow c (c_1 ;c_2 )) = ]$

$[= (overrightarrow {a_1 ;a_2 } ) + (overrightarrow {b_1 + c_1 ;b_2 + c_2 } ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } ),]$

$[(overrightarrow a (a_1 ;a_2 ) + overrightarrow b (overrightarrow {b_1 ;b_2 } )) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 ;a_2 + b_2 } ) + overrightarrow c (c_1 ;c_2 ) = ]$

$[= (overrightarrow {a_1 + b_1 + c_1 ;a_2 + b_2 + c_2 } );]$

$[3)overrightarrow a (a_1 ;a_2 ) + overrightarrow 0 (0;0) = (overrightarrow {a_1 + 0;a_2 + 0} ) = (overrightarrow {a_1 ;a_2 } ) = overrightarrow a .]$

Теорема

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Доказательство:

Для точек A (x₁;y₁), B (x₂;y₂), C (x₃;y₃)

$[overrightarrow {AB} (x_2 - x_1 ;y_2 - y_1 ),]$

$[overrightarrow {BC} (x_3 - x_2 ;y_3 - y_2 ),]$

$[overrightarrow {AC} (x_3 - x_1 ;y_3 - y_1 ).]$

Тогда

$[overrightarrow {AB} + overrightarrow {BC} = (overrightarrow {x_2 - x_1 + x_3 - x_2 ;y_2 - y_1 + y_3 - y_2 } ) = ]$

$[= (overrightarrow {x_3 - x_1 ;y_3 - y_1 } ) = overrightarrow {AC} .]$

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Пример.

Построить сумму векторов

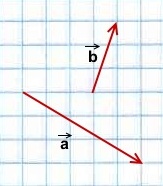
Решение:

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

вектор

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

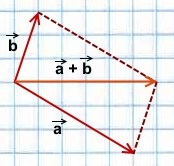
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

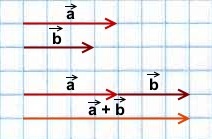
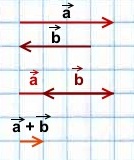
Сложение коллинеарных векторов

1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

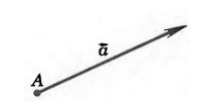
Определение 1

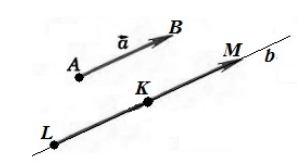
Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

Вектор $overrightarrow{a}$ — нулевой.

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.
Вектор $overrightarrow{a}$ — ненулевой.

Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ — конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Сложение векторов. Правило треугольника

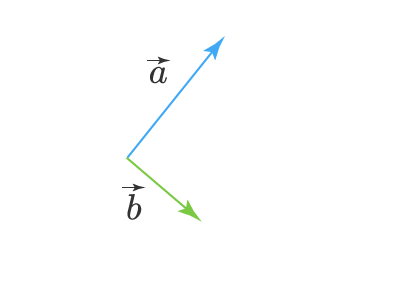
Пусть нам даны векторы $overrightarrow{a}$ и $overrightarrow{b}$.

Определение 2

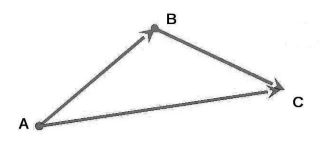
Суммой векторов $overrightarrow{a}+overrightarrow{b}$ называется вектор $overrightarrow{c}=overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $overrightarrow{AB}=overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $overrightarrow{BC}=overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис. 3).

Рисунок 3. Сумма векторов

«Сложение векторов. Как найти сумму векторов» 👇

Замечание 1

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $overrightarrow{a}$ выполняется равенство

[overrightarrow{a}+overrightarrow{0}=overrightarrow{a}]
Для любых произвольных точек $A, B и C$ выполняется равенство

[overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}]

Замечание 2

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Теорема 2

Для любых треух векторов $overrightarrow{a}, overrightarrow{b} и overrightarrow{c}$ справедливы следующие два закона:

Переместительный закон:

[overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}]

Сочетательный закон:

[left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)]

Доказательство.

Переместительный закон:

Пусть векторы $overrightarrow{a} и overrightarrow{b}$ не коллинеарны.

Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $overrightarrow{a}+overrightarrow{b} и overrightarrow{b}+overrightarrow{a}$. Получим следующий рисунок (рис 4).

Рисунок 4. Иллюстрация переместительного закона

Очевидно, что $overrightarrow{a}+overrightarrow{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, а $overrightarrow{b}+overrightarrow{a}=overrightarrow{AD}+overrightarrow{DC}=overrightarrow{AC}$

Следовательно, $overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}$.
Пусть векторы $overrightarrow{a} и overrightarrow{b}$ коллинеарны.

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow{a}+overrightarrow{b}right|и |overrightarrow{b}+overrightarrow{a}|$.

Сочетательный закон:

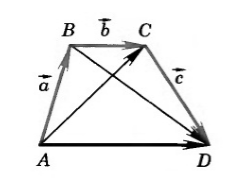
Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $overrightarrow{AB}=overrightarrow{a}$, от полученной точки $B$ — вектор $overrightarrow{BC}=overrightarrow{b}$ и от точки $C$ — вектор $overrightarrow{CD}=overrightarrow{c}$ (Рис. 5).

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

Следовательно, $left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)$.

Теорема доказана.

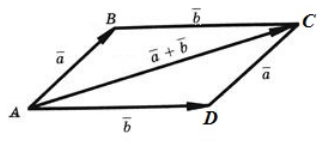
Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $overrightarrow{a}$ и $overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $overrightarrow{AB}=overrightarrow{a}$ и $overrightarrow{AD}=overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $overrightarrow{a}+overrightarrow{b}=overrightarrow{AC}$.

Пример задачи на сложение векторов

Пример 1

Дан четырехугольник $ABCD$. Доказать, что $overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AD}$

Рисунок 6.

Доказательство.

Воспользуемся свойством правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

[overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AC}+overrightarrow{CD}=overrightarrow{AD}]

ч. т. д.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В статье Понятие вектора мы сказали, что векторы можно складывать друг с другом. Рассмотрим этот вопрос подробнее.

Пусть нам даны два вектора a⃗vec{a} и b⃗vec{b}. Что понимать под суммой этих двух векторов, то есть под a⃗+b⃗vec{a}+vec{b}? Во первых, сумма двух векторов это вектор. То есть, если мы складываем два вектора (две стрелки) то снова получаем вектор (стрелку). Существуют два способа (или правила) как можно складывать векторы. Они, конечно, дают один и тот же самый результат. Говорят о правиле треугольника и правиле параллелограмма. Оба эти правила графические, то есть сумма векторов находится путем геометрического построения. О сумме векторов, выраженной через координаты векторов речь пойдет в другой статье.

Правило треугольника

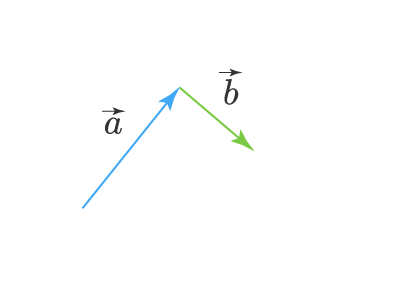
Вот нам даны два вектора a⃗vec{a} и b⃗vec{b}. Для того чтобы найти их сумму, пользуясь правилом треугольника, нужно чтобы начало одного из векторов находилось в точке конца другого вектора. То есть, чтобы точки начала одного вектора и конца другого вектора совпадали. Но что делать, если это не так? Для этого нужно параллельно перенести любой из векторов так чтобы это условие выполнялось. Например, пусть вначале векторы у нас расположены так:

Перенесем теперь вектор b⃗vec{b} параллельно самому себе так чтобы его начало совпало с концом вектора a⃗vec{a}. Получим:

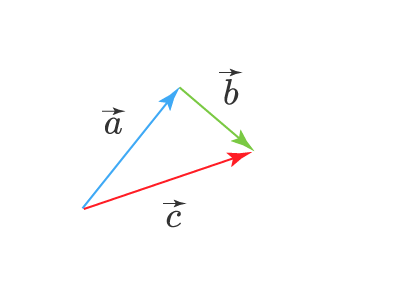
Теперь, чтобы найти сумму этих векторов, нужно провести вектор (стрелку) из начала вектора a⃗vec{a} в конец вектора b⃗vec{b}. Получим вектор c⃗=a⃗+b⃗vec{c}=vec{a}+vec{b}:

Правило параллелограмма

Решим ту же задачу вторым способом. Для этого нам нужно сделать так чтобы векторы a⃗vec{a} и b⃗vec{b} исходили из одной точки, то есть, чтобы точки начала этих векторов совпали. Получим:

Теперь построим на этих двух векторах параллелограмм. Суммой векторов a⃗vec{a} и b⃗vec{b} будет вектор, совпадающий с диагональю этого параллелограмма, и начало этого суммарного вектора c⃗vec{c} будет совпадать с началом векторов a⃗vec{a} и b⃗vec{b}:

На самом деле, по своему смыслу, оба эти правила это одно и то же правило. Просто так уж вышло, что в зависимости от построения треугольника или параллелограмма, говорят о соответствующем правиле складывания векторов.

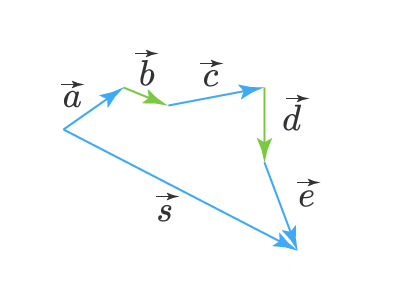
Сумма любого числа векторов

Складывать между собой можно не только два вектора, но и любое их количество. Для этого удобно воспользоваться правилом треугольника. Пусть у нас есть векторы a⃗,b⃗,c⃗,d⃗,e⃗vec{a}, vec{b}, vec{c}, vec{d}, vec{e}. Пусть мы перенесли параллельно векторы так, что начало каждого последующего вектора берет свое начало в конце предыдущего вектора, тогда сумма этих векторов, вектор s⃗vec{s} — это вектор с началом, совпадающим с началом первого вектора (вектора a⃗vec{a}) и концом, совпадающим с концом последнего вектора (вектора e⃗vec{e}):

Тест по теме “Сумма векторов”

Источник

Конспект
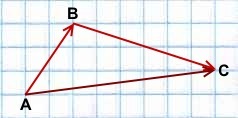
Рассмотрим ситуацию.
Стартовав из пункта A, туристы прошли 4 километра на запад, а затем 3 километра на север. В результате этих двух перемещений туристы переместились из пункта А в пункт С. Поэтому результирующее перемещение можно представить вектором (AC) ⃗. Перемещение из пункта А в пункт С складывается из перемещения из пункта А в пункт В и перемещения из пункта В в пункт С, поэтому вектор (AC) ⃗ естественно назвать суммой векторов (AB) ⃗ и (BC) ⃗.
Этот пример приводит нас к понятию суммы векторов: (AB) ⃗+ (BC) ⃗= (AC) ⃗
Даны два вектора: a ⃗ и b ⃗. Отметим произвольную точку А и отложим от этой точки вектор (AB) ⃗, равный вектору a ⃗.
(AB) ⃗ = a ⃗
Затем от точки В отложим вектор (BC) ⃗, равный вектору b ⃗.
(BC) ⃗ = b ⃗.
Вектор (AC) ⃗ называется суммой векторов a ⃗ и b ⃗.
Это правило сложения векторов называется правилом треугольника.
(AC) ⃗ = a ⃗ + b ⃗.
Правило треугольника можно сформулировать следующим образом: для произвольных точек А, В и С сумма векторов (AB) ⃗и (BC) ⃗ равна вектору (AC) ⃗: (AB) ⃗+ (BC) ⃗= (AC) ⃗.
Складывая по правилу треугольника произвольный вектор a ⃗ с нулевым вектором, получаем, что для любого вектора a ⃗ справедливо равенство a ⃗ + 0 ⃗ = a .
Докажем законы сложения векторов: переместительный и сочетательный.
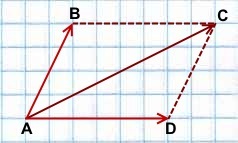
От произвольной точки А отложим векторы (AB) ⃗, равный вектору и вектор (AD) ⃗, равный вектору b ⃗.
(AB) ⃗ = a ⃗, (AD) ⃗ = b ⃗.
На векторах (AB) ⃗ и (AD) ⃗ построим параллелограмм АВСD.

По правилу треугольника вектор (AC) ⃗ равен сумме векторов (AB) ⃗и (BC) ⃗. С другой стороны, вектор (AC) ⃗ равен сумме векторов (AD) ⃗ и (DС) ⃗.

(AC) ⃗ = (AB) ⃗+ (BC) ⃗ = a ⃗ + b ⃗.
(AC) ⃗ = (AD) ⃗ + (DC) ⃗ = b ⃗ +(a) ⃗.
a ⃗ + b ⃗= b ⃗ + (a) ⃗ (переместительный закон)
При доказательстве переместительного закона сложения векторов мы обосновали правило сложения неколлинеарных векторов – правило параллелограмма.
Чтобы сложить неколлинеарные векторы a ⃗ и b ⃗, нужно выбрать произвольную точку и отложить от неё векторы, равные данным. На этих векторах построить параллелограмм. Вектор с началом в выбранной точке и являющийся диагональю параллелограмма, будет суммой данных векторов a ⃗ и b ⃗.
Докажем ещё одно свойство сложения векторов: сочетательный закон.
Выберем произвольную точку А и отложим от неё вектор (AB) ⃗, равный(a) ⃗, от точки В – вектор (BC) ⃗, равный вектору b ⃗, а от точки С – вектор (CD) ⃗, равный вектору c ⃗.

Пользуясь правилом треугольника, найдём значения суммы трёх данных векторов.
(a ⃗ + b ⃗) + c ⃗ = (AB) ⃗+ (BC) ⃗ + (CD) ⃗ = (AC) ⃗ + (CD) ⃗ = (AD) ⃗.
Найдём сумму этих же векторов, изменив порядок действий.
Построим сумму векторов b ⃗ и c ⃗, а затем к вектору a ⃗ прибавим получившийся результат.
a ⃗+ (b ⃗+ c ⃗) = (AB) ⃗+ ((BC) ⃗ + (CD) ⃗) = (AB) ⃗ + (BD) ⃗ = (AD) ⃗.
Мы доказали, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
При сложении нескольких векторов пользуются правилом многоугольника: при сложении векторов их последовательно откладывают один за другим, так чтобы начало следующего вектора совпадало с концом предыдущего. Вектор, соединяющий начало первого вектора с концом последнего, будет суммой данных векторов.
p ⃗ = (a₁) ⃗+ (a₂) ⃗ + (a₃) ⃗ + (a₄) ⃗+ (a₅) ⃗

Источник