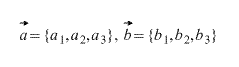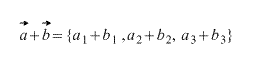Как найти сумму векторов заданных графически - Исправление недочетов и поиск решений вместе с Examum.ru

Сложение и вычитание векторов

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = < b ₁ ; b ₂ ; . ; b_n > можно найти, воспользовавшись следующими формулами:

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Сумма векторов: графический метод, примеры, решенные упражнения.

Содержание:

В векторная сумма это операция сложения между векторами, которая приводит к другому вектору. Векторы характеризуются величиной, а также направлением и смыслом. Следовательно, в общем случае невозможно сложить их, как это было бы со скалярными величинами, то есть путем сложения чисел.

Вектор, полученный из суммы нескольких векторов, называется результирующий вектор. В механике говорят о Равнодействующая сила, которая представляет собой векторную сумму всех сил, действующих на тело. Эта равнодействующая эквивалентна множеству или системе сил.

Чтобы полностью указать вектор суммы, необходимо указать величину и единицу, направление и смысл.

Важно отметить, что при сложении векторов они должны представлять одну и ту же физическую величину, поэтому векторная сумма является однородной операцией. Это означает, что мы можем добавлять одну силу к другой, но не силу со смещением, поскольку результат не имеет смысла.

Для нахождения результирующего вектора доступны несколько методов: графический и аналитический. Чтобы найти векторные суммы с помощью графических методов, мы начнем с простого представления вектора, а именно с ориентированного сегмента или стрелки, подобного этому:

Векторы обозначаются жирными буквами в печатном тексте или стрелкой над буквой, чтобы отличать их от соответствующих величин или скалярных величин. Например, величина вектора vЭто просто v.

Графический метод сложения векторов

Чтобы добавить более двух копланарных векторов, полигональный метод или метод траверса, который состоит из трансляции себя параллельно каждому из векторов слагаемых. Характерной чертой векторов является то, что они инвариантны относительно сдвига, поэтому мы будем использовать это свойство для определения суммы.

Мы начинаем с любого из векторов, так как сложение векторов коммутативно и порядок слагаемых не влияет на сумму. Затем переводится второй вектор, сопоставляя его начало с концом первого.

Затем он переносится к следующему вектору и помещается следующим, следуя той же процедуре, которая заключается в совпадении начала координат с концом предыдущего. Продолжайте таким образом, пока не будет установлен последний вектор.

Результирующий вектор — это тот, который соединяет начало первого со свободным концом последнего. Название этого метода происходит от получившегося рисунка: многоугольник.

пример

Возьмем для примера сумму двух векторов или Y v показано на рисунке выше.

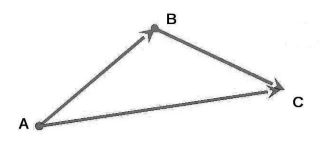
Начиная с вектора или, переехал в вектор v чтобы его начало совпадало с концом первого. Результирующий вектор ш взят из происхождения или до конца v, образуя трехстороннюю фигуру: треугольник. Поэтому в этом частном случае процедура называется метод треугольника.

Обратите внимание на важную деталь: величина или модуль результирующего вектора не является суммой модулей добавленных векторов. Фактически, это почти всегда меньше, если векторы не параллельны.

Посмотрим, что происходит в этом случае ниже.

Частный случай: сумма параллельных векторов

Описанный метод применим и к частному случаю, когда векторы параллельны. Рассмотрим следующий пример:

Оставлено вектору v в исходном положении и переводится в вектор или таким образом, что его происхождение совпадает с концом v. Теперь нарисован вектор, начиная с начала координат v и заканчивает конец или.

Это результирующий вектор ш а его размер — это сумма размеров слагаемых. Направление и смысл трех векторов одинаковы.

Результирующий вектор имеет максимальный модуль, если слагаемые образуют угол 0º друг с другом, как в примере. Если векторы расположены под углом 180º друг к другу, то результирующий вектор имеет минимальный модуль.

Примеры сложения векторов

— Смещения

Велосипедист проезжает сначала 3 км в северном направлении, а затем 4 км на запад. Ваше перемещение, которое мы называем р, легко найти с помощью метода треугольника плюс система отсчета, где отмечены стороны света:

Шаги к векторному сложению

— Начальная точка совпадает с началом системы отсчета.

-По осям координат выбран масштаб, который в данном случае составляет 1 см = 1 км.

-Первое смещение нарисовано в масштабе d_1.

-Следующий d₁ второе смещение нарисовано d₂, также в масштабе.

-В результате смещения р — вектор, идущий от начала до конца d₂.

-Размерр измеряется градуированной линейкой, легко проверить, что R = 5.

-Наконец, угол, который р форма по горизонтали измерена с помощью транспортира и составляет θ = 37 0

— Результирующая скорость

Пловец хочет пересечь реку и для этого плывет со скоростью 6 км / ч перпендикулярно берегу, но его отклоняет течение со скоростью 4 км / ч.

Чтобы узнать его итоговую скорость, добавляются векторы скорости пловца, изображенного вертикально, и вектора скорости, отображаемого горизонтально.

Графическим методом получается результирующая скорость. v_р:

Отклонение, которое испытывает пловец, можно рассчитать следующим образом:

θ = arctg (4/6) = 33,7º вправо от начального направления

Величина его скорости увеличивается благодаря тому, что скорость реки складывается векторно. Его можно найти, аккуратно установив масштаб, как в примере выше.

Или с помощью тригонометрических соотношений 33,7º:

грех 33,7º = 4 / v_р

v_р = 4 / sin 33,7º = 7,21 км / ч

Упражнение решено

На частицу действуют следующие силы, величины которых указаны ниже:

Найдите равнодействующую силу.

Решение

Мы можем складывать графически, начиная с любого из векторов, поскольку векторная сумма коммутативна.

На рисунке A мы начали с F₁. Устанавливая масштаб, с помощью линейки и квадрата переносятся другие векторы, чтобы расположить их один за другим.

Вектор F_р направлено от происхождения F₁ до конца F₄. Его величина составляет 5,2 Н, и он образует угол 26,5 ° по отношению к горизонту.

На рисунке B была решена та же проблема, начиная с F₃ и заканчивая F₄, чтобы сравнятьсяF_р .

Многоугольники разные, но результат тот же. Читатель может провести тест, снова изменив порядок векторов.

Ссылки

Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.

Смехотерапия: история, методики, польза

Психология и питание: важность эмоционального питания

Как найти сумму векторов

Формула

Примеры нахождения суммы векторов

Задание. Найти сумму векторов $bar+bar$, $bar=(2;0)$ и $bar=(1;3)$

Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

Остались вопросы?

Здесь вы найдете ответы.

Поможем выполнить
любую работу

Все еще сложно?

Наши эксперты помогут разобраться

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

источники:

http://ru1.warbletoncouncil.org/suma-de-vectores-14717

http://www.webmath.ru/poleznoe/formules_13_1.php

Источник

Содержание:

Формула
Примеры нахождения суммы векторов

Формула

Чтобы найти сумму векторов $bar{a}+bar{b}$, которые заданны координатами
$bar{a}=(a_x;a_y)$ и $bar{b}=(b_x;b_y)$, необходимо сложить соответствующие
координаты этих векторов,
то есть

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y}right)$$

В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их сумма равна

$$bar{a}+bar{b}=left(a_{x}+b_{x} ; a_{y}+b_{y} ; a_{z}+b_{z}right)$$

Примеры нахождения суммы векторов

Пример

Задание. Найти сумму векторов
$bar{a}+bar{b}$,
$bar{a}=(2;0)$ и
$bar{b}=(1;3)$

Решение. Для нахождения суммы векторов, сложим их соответствующие координаты

$$bar{a}+bar{b}=(2 ; 0)+(1 ; 3)=(2+1 ; 0+3)=(3 ; 3)$$

Ответ. $bar{a}+bar{b}==(3 ; 3)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти суммы векторов
$bar{a}+bar{b}$,
$bar{a}+bar{c}$,
$bar{b}+bar{c}$ и
$bar{a}+bar{b} +bar{c}$, если
$bar{a}=(1;-1;0)$,
$bar{b}=(3;2;-1)$ и
$bar{c}=(4;2;-1)$

Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:

$$bar{a}+bar{b}=(1+3 ;-1+2 ; 0+(-2))=(4 ; 1 ;-2)$$
$$bar{a}+bar{c}=(1+4 ;-1+2 ; 0+(-1))=(5 ; 1 ;-1)$$
$$bar{b}+bar{c}=(3+4 ; 2+2 ;-2+(-1))=(7 ; 4 ;-3)$$
$$bar{a}+bar{b}+bar{c}=(1+3+4 ;-1+2+2 ; 0+(-2)+(-1))=(8 ; 3 ;-3)$$

Ответ. $bar{a}+bar{b}=(4 ; 1 ;-2)$ , $bar{a}+bar{c}=(5 ; 1 ;-1)$ , $bar{b}+bar{c}=(7 ; 4 ;-3)$ , $bar{a}+bar{b}+bar{c}=(8 ; 3 ;-3)$

Читать дальше: как найти разность векторов.

Источник

Физика > Графическое добавление и вычитание векторов

Векторы можно добавлять и отнимать на графике при помощи прикладывания их к концам осей.

Задача обучения

Научиться разбираться в процессе сложения и вычитания векторов на графике.

Основные пункты

Чтобы добавить вектор, приложите первый набор осей с концом вначале координат. Отправьте вектор в голову предыдущего вектора. Когда закончите, проведите прямую линию от начала координат к голове последнего вектора. Эта линия отображает сумму векторов.
Чтобы отнять векторы, проделайте все с предыдущего пункта, но переверните вектор, который собираетесь убрать по осям, а затем прибавьте его к голове.
Сложение или вычитание предоставляет результирующий вектор.

Термины

Начало – центр координатной оси, отображенный как 0 по всем осям.
Оси координат – набор перпендикулярных линий, отображающих координаты с горизонтальным и вертикальным положениями.

Пример

В методе векторного сложения от головы до хвоста необходимо поставить первый вектор вдоль набора осей координат. Затем добавьте хвост следующего к голове первого. Нарисуйте новый вектор от начала координат к голове последнего. Этот новый вектор выступает суммой двух изначальных.

Добавление и вычитание векторов

Анализировать физические величины проще всего через добавление векторов. Так как это графические визуализации, то и операции с ними можно проводить прямо на графике.

Добавление часто называют «голова-хвост». Главное следовать правилам сложения векторов. Все начинается с изображения набора осей координат. Далее вычеркните первый вектор с хвостом (базой) в начале системы координат. Если добавляете, то неважно, какой вектор отобразите первым, но для отнимания проверьте, чтобы первый вектор был изначальным.

Дальше нужно нарисовать следующий вектор так, чтобы его хвост начинался с головы предыдущего (со стороны стрелки). Продолжайте повторять это с каждым вектором, пока они все не объединятся. В итоге, проведите прямую линию от начала координат к голове последнего вектора. Вы получили векторную сумму.

Важно выложить первый вектор вдоль набора оси координат. Далее поставьте хвост следующего к голове первого. Изобразите новый вектор от начала координат к голове последнего. Получившаяся линия отображает общую сумму

В случае с правилом вычитания векторов схема та же. Проверьте, что первый вектор выступает тем, от которого нужно отнимать. Далее добавляйте векторы, но обратной стороной. То есть, переверните вычитаемый вектор относительно осей и присоедините хвост к голове. Чтобы сделать переворот, определите голову туда, где располагался хвост, а хвост поставьте на место головы.

Источник

В механике существуют два типа величин:

скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

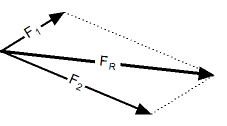
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

правило параллелограмма
правило треугольника
тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

Процедура сложения векторов по правилу параллелограмма заключается в следующем:

нарисовать первый вектор, учитывая его величину и направление
от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:

нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

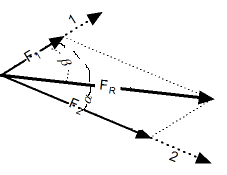Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:

F_рез. = [ F₁² + F₂² -2 F₁ F₂ cos(180^о-α) ]^1/2 (1)
- где
  - F = числовое значение вектора
  - α = угол между векторами 1 и 2

Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:

β = arcsin[ F₂*sin(180^o-α) / F_R] (2)
- где
  - α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80^o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН)² + (8 кН)² — 2 (5 кН)(8 kН) cos(180^o — (80^o)) ]^1/2

= 10,14кН

Угол между результирующей силой и первой силой равен:

β= arcsin[ (8кН) sin(180^o — (80^o)) / (10,14кН)]

= 51^o

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180^o — (80^o)) / (10,2 кН)]

= 29^o

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Распечатать: Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма.

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Определение 1

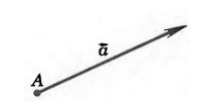
Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

Вектор $overrightarrow{a}$ — нулевой.

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.
Вектор $overrightarrow{a}$ — ненулевой.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

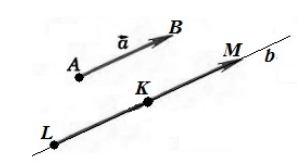
Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ — конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Сложение векторов. Правило треугольника

Пусть нам даны векторы $overrightarrow{a}$ и $overrightarrow{b}$.

Определение 2

Суммой векторов $overrightarrow{a}+overrightarrow{b}$ называется вектор $overrightarrow{c}=overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $overrightarrow{AB}=overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $overrightarrow{BC}=overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис. 3).

Рисунок 3. Сумма векторов

«Сложение векторов. Как найти сумму векторов» 👇

Замечание 1

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $overrightarrow{a}$ выполняется равенство

[overrightarrow{a}+overrightarrow{0}=overrightarrow{a}]
Для любых произвольных точек $A, B и C$ выполняется равенство

[overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}]

Замечание 2

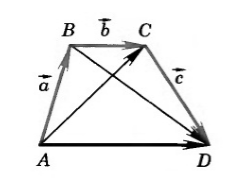
Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Теорема 2

Для любых треух векторов $overrightarrow{a}, overrightarrow{b} и overrightarrow{c}$ справедливы следующие два закона:

Переместительный закон:

[overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}]

Сочетательный закон:

[left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)]

Доказательство.

Переместительный закон:

Пусть векторы $overrightarrow{a} и overrightarrow{b}$ не коллинеарны.

Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $overrightarrow{a}+overrightarrow{b} и overrightarrow{b}+overrightarrow{a}$. Получим следующий рисунок (рис 4).

Рисунок 4. Иллюстрация переместительного закона

Очевидно, что $overrightarrow{a}+overrightarrow{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, а $overrightarrow{b}+overrightarrow{a}=overrightarrow{AD}+overrightarrow{DC}=overrightarrow{AC}$

Следовательно, $overrightarrow{a}+overrightarrow{b}=overrightarrow{b}+overrightarrow{a}$.
Пусть векторы $overrightarrow{a} и overrightarrow{b}$ коллинеарны.

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow{a}+overrightarrow{b}right|и |overrightarrow{b}+overrightarrow{a}|$.

Сочетательный закон:

Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $overrightarrow{AB}=overrightarrow{a}$, от полученной точки $B$ — вектор $overrightarrow{BC}=overrightarrow{b}$ и от точки $C$ — вектор $overrightarrow{CD}=overrightarrow{c}$ (Рис. 5).

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

Следовательно, $left(overrightarrow{a}+overrightarrow{b}right)+overrightarrow{c}=overrightarrow{a}+left(overrightarrow{b}+overrightarrow{c}right)$.

Теорема доказана.

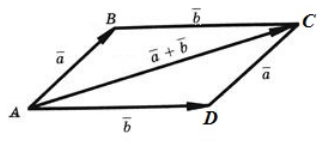
Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $overrightarrow{a}$ и $overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $overrightarrow{AB}=overrightarrow{a}$ и $overrightarrow{AD}=overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $overrightarrow{a}+overrightarrow{b}=overrightarrow{AC}$.

Пример задачи на сложение векторов

Пример 1

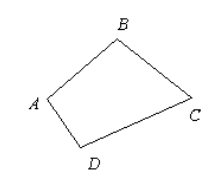
Дан четырехугольник $ABCD$. Доказать, что $overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AD}$

Рисунок 6.

Доказательство.

Воспользуемся свойством правила треугольника $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, получим:

[overrightarrow{AB}+overrightarrow{BC}+overrightarrow{CD}=overrightarrow{AC}+overrightarrow{CD}=overrightarrow{AD}]

ч. т. д.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник