Углы параллелограмма равны, соответственно, 30° и (180 — 30 = 150°). Тогда первая высота — катет прямоугольного треугольника с гипотенузой 10, совпадающей с малой стороной параллелограмма, противолежащий углу в 30° — значит, она равна 10:2 = 5 см.
Вторая высота параллелограмма — катет прямоугольного треугольника с гипотенузой 20, совпадающей с большей стороной параллелограмма, противолежащий углу в 30° — значит, она равна 20:2 = 10 см.
Сумма высот равна 5 + 10 = 15 см.
В параллелограмме противоположные стороны друг другу параллельны, а прилежащие находятся образуют определенный угол, поэтому чтобы определить большинство параметров параллелограмма нужно знать кроме сторон высоту или угол, их соединяющий. Если заданы стороны и высота, то одними из первых можно рассчитать периметр и площадь параллелограмма. Периметр параллелограмма, зная стороны, выглядит как их удвоенная сумма, а площадь является произведением высоты и стороны, на которую она опущена.
P=2(a+b)
S=ah_a=bh_b
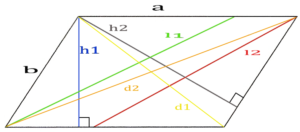
Чтобы иметь возможность продолжать расчеты, необходимо найти углы между сторонами α и β. Используя прямоугольный треугольник, образованный высотой со стороной параллелограмма, выводим их взаимосвязь в тригонометрическое отношение. Затем, зная один из углов, в зависимости от того, какая высота была дана, отнимаем его из 180 градусов, чтобы найти второй. (рис.106.1)
sinα=h_b/a
sinβ=h_a/b
α=180°-β
β=180°-α
Зная углы и стороны, можно найти диагонали параллелограмма по теореме косинусов в треугольниках, которые они образуют со сторонами. Каждая диагональ будет равна корню из суммы квадратов сторон параллелограмма и разности удвоенного их произведения на косинус угла между ними. (рис.106.2)
d_1=√(a^2+b^2-2ab cosβ )
d_2=√(a^2+b^2-2ab cosα )
Используя эту же теорему косинусов, можно найти угол между диагоналями в одном из четырех треугольников, образованных ими, где сторонами являются половины диагоналей и одна из сторон параллелограмма. (рис.106.3)
cosγ=(〖d_1/4〗^2+〖d_2/4〗^2-a^2)/((d_1 d_2)/4)=(〖d_1〗^2+〖d_2〗^2-4a^2)/(2d_1 d_2 )
cosδ=(〖d_1〗^2+〖d_2〗^2-4b^2)/(2d_1 d_2 )
Биссектрисы параллелограмма, проведенные из углов α и β, образуют равнобедренные треугольники, в которых сама биссектриса является основанием, а боковыми конгруэнтными сторонами становится меньшая сторона параллелограмма. Треугольник считается равнобедренным, так как из свойств биссектрисы и суммы углов в треугольнике следует, что углы при основании такого треугольника конгруэнтны. Используя теорему косинусов, можно найти биссектрисы параллелограмма через стороны. (рис. 106.4)
l_α=√(2a^2-2a^2 cosβ )=a√(2-2 cosβ )
l_β= b√(2-2 cosα )
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
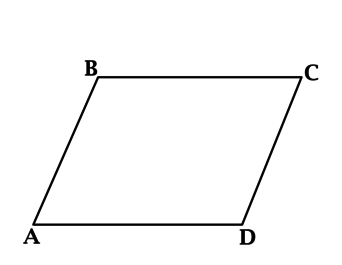
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
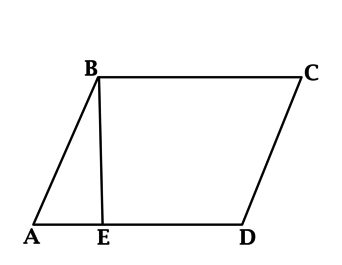
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
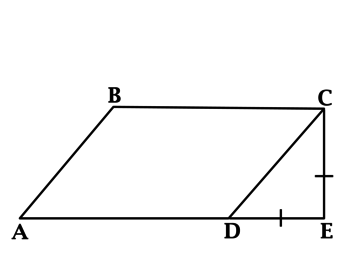
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни
Четырёхугольник, у которого стороны, находящиеся напротив друг друга параллельны и равны друг другу,
называется параллелограммом. Отрезок перпендикулярной прямой, проходящей от любой точки прямой, на
которой лежит одна из сторон параллелограмма через прямую, на которой расположена противоположная
сторона данной фигуры, является высотой параллелограмма. Высот параллелограмма можно провести
бесконечное множество через разные точки, но они неизменно будут перпендикулярны двум сторонам
фигуры.
- Высота параллелограмма через площадь и основание
- Высота параллелограмма через боковую сторону и острый угол
при основании - Высота параллелограмма через длину отрезка, образованного
на основании и боковую сторону - Высота параллелограмма через длину отрезка, образованного
на основании и диагональ
Через площадь и основание
Высота параллелограмма равна отношению площади к основанию.
h = S / a
где h – длина высоты параллелограмма, S – площадь, a – длина основания.
Цифр после
запятой:
Результат в:
Пример. На рисунке представлены пара абсолютно одинаковых параллелограммов. На левом
обозначена длина стороны (основания) в 6 единиц и проходящие через нее в разных точках высоты в 4
единицы.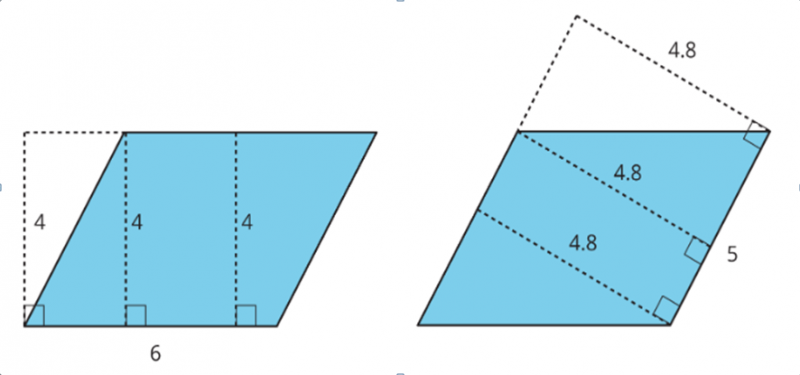
правом обозначена длина стороны (основания) в 5 единиц и проходящие через нее в разных точках высоты
в 4,8 единиц. Площадь параллелограмма можно вычислить умножением длины высоты на длину той стороны
(основания), которой эта высота перпендикулярна. Результат умножения будет одинаков для любой 2 двух
пар высота-основание. В рассматриваемом случае: 4 × 6 = 24; 4,8 × 5 = 24.
Можно визуально убедиться в этом, если разрезать фигуру и переставив части так, как показано на
рисунке.
Исходя из полученного, путем обратного подсчета можно вывести правило для определения высоты из
заданной площади и основания. В приведенном примере расчет будет выглядеть следующим образом: 24 / 6 = 4; 24 / 5 = 4,8.
Через длину отрезка, образованного на основании и диагональ
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и диагонали
производится также с использованием теоремы Пифагора. Высота в этом случае будет равна квадратному
корню из разницы диагонали и отрезка на основании.
h = √(d² — A2²)
где d — диагональ, A2 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 47 см, отрезок образованный на основании равен
34 см, тогда получим h = √(b² — A1²) = √(47² — 34²) = 32,4 см.
Через боковую сторону и острый угол при основании
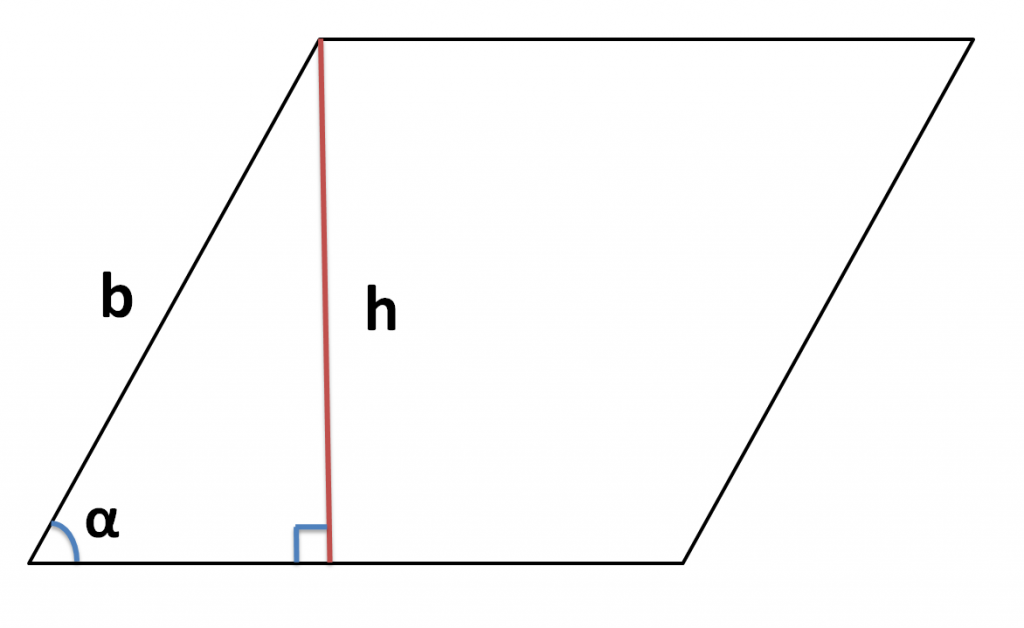
Если от тупого угла параллелограмма провести к основанию высоту, то образуется прямоугольный
треугольник, как показано на рисунке ниже. Если нам известна величина острого угла и длина боковой
стороны, то можно вычислить высоту через формулу синуса, который определяется как отношение катета к
гипотенузе. Роль катета здесь играет высота, а боковая сторона является гипотенузой. Соответственно
высота здесь будет равна произведению длины боковой стороны на синус острого угла.
h = b * sinα
где b — боковая сторона, sin α — острый угол при основании.
Цифр после
запятой:
Результат в:
Если известна величина тупого угла параллелограмма, то величину острого можно получить, отняв
величину тупого угла от 180 градусов.
Пример. Пусть боковая сторона b равна 115 см, острый угол при основании α равен 65º,
тогда получим h = b * sinα = 115 * sin 65 = 104 см.
Через длину отрезка, образованного на основании и боковую сторону
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и боковой
стороне производится с использованием теоремы Пифагора. Высота будет равна квадратному корню из
разницы квадратов боковой стороны и диагонали.
h = √(b² — A1²)
где b — боковая сторона, A1 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 39 см, отрезок образованный на основании равен
16 см, тогда получим h = √(b² — A1²) = √(39² — 16²) = 35,6 см.
Пирамида определяется как трехмерная структура – многогранник, в основе которой лежит многоугольник.
В основании пирамиды находится многоугольник. Углы многоугольника соединены линиями – боковыми
ребрами с одной точкой, которая в пирамиде именуется как вершина. Треугольники, образованные парами
соседних боковых ребер и стороной основания называются боковыми гранями.
В основании правильной пирамиды лежит правильный многоугольник (тот у которого все стороны равны
между собой). У правильной пирамиды длина боковых ребер одинаковая. Соответственно правильная
пирамида образована боковыми гранями, являющимися равными равнобедренными треугольниками,
соединенными с основанием.
Апофемами в пирамиде называют отрезки прямых, проведенных от вершины перпендикулярно к основаниям.
Также, одновременно апофемы являются высотами треугольников – боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему грани.
Установлено, что умение вычислять длину апофемы, было востребовано с древнейших времен для
строительства сооружений. Предположительно, перед возведением подобных сооружений предварительные
размеры могли быть отрегулированы древними инженерами с помощью натянутых шнуров. Расшифровка
древнеегипетских иероглифов дает перевод значения понятия землемера как «натяжителя веревок».
Умение вычислять высоту параллелограммов, было востребовано с древнейших времен для проверки
правильности измерений земельных участков. Множество древних народов тысячи лет назад воздвигали
пирамиды и курганы для различных целей. Современные измерения позволяют утверждать, что некоторые их
них точно ориентированы – как по сторонам света, так и в трехмерном измерении по созвездиям.
Вероятно, часть из этих сооружений использовалась для определения орбиты Земли относительно звезд.
Эти сведения использовались для определения времени начала различных сельскохозяйственных работ. От
этого зависела урожайность, а значит вопрос выживания народов. Таким образом, вычисление апофемы
позволяло точно ориентировать пирамиду в пространстве и спасало жизни людей.
Быстро вычислить высоту параллелограмма позволит этот удобный онлайн-калькулятор. С его помощью можно определить не только высоту параллелограмма, но и такие величины как площадь, биссектриса, периметр, диагональ, углы параллелограмма вместе с подробными формулами расчета.
Не забудьте добавить страницу в закладки, чтобы всегда иметь под рукой удобную шпаргалку по геометрии!
Введите данные:
Длинная сторона (a)
Короткая сторона (b)
Ключевой показатель *
Значение ключевого показателя *
Округление:
Знаков после запятой
* — обязательно заполнить