Как найти суммы в шестнадцатиричной системе счисления

Шестнадцатеричный калькулятор онлайн

  1. Главная
  2. /
  3. Информатика
  4. /
  5. Шестнадцатеричный калькулятор онлайн

Если вам необходимо произвести математические операции в шестнадцатеричной системе счисления воспользуйтесь нашим онлайн калькулятором:

Просто введите шестнадцатеричные числа, выберите операцию и получите результат.

Калькулятор может производить следующие действия:

  • сложение +
  • вычитание −
  • умножение ×
  • деление ÷
  • логическое И (AND)
  • логическое ИЛИ (OR)
  • исключающее ИЛИ (XOR)

Сложение в шестнадцатеричной системе счисления

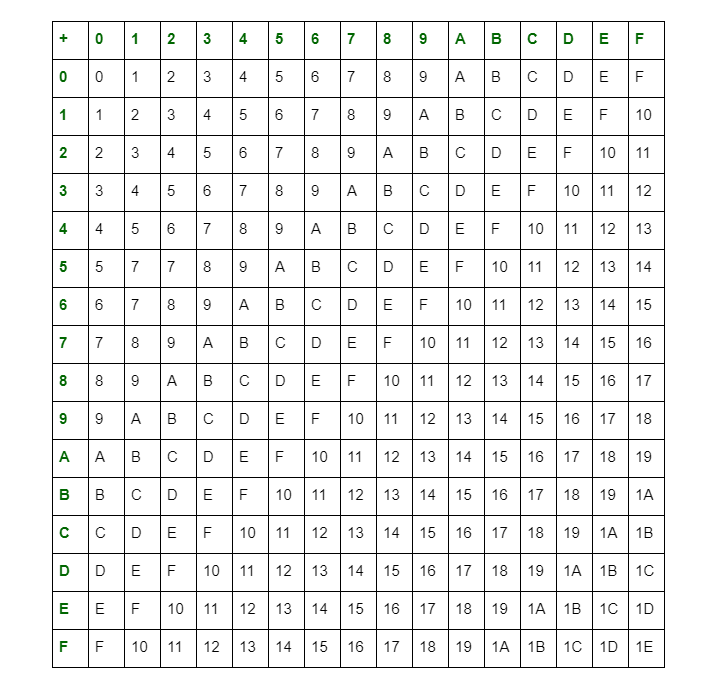
Сложение двух шестнадцатеричных чисел производится столбиком, как и в десятичной системе, но по следующим правилам:

+ 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0 1 2 3 4 5 6 7 8 9 A B C D E F
1 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 2 3 4 5 6 7 8 9 A B C D E F 10 11
3 3 4 5 6 7 8 9 A B C D E F 10 11 12
4 4 5 6 7 8 9 A B C D E F 10 11 12 13
5 5 6 7 8 9 A B C D E F 10 11 12 13 14
6 6 7 8 9 A B C D E F 10 11 12 13 14 15
7 7 8 9 A B C D E F 10 11 12 13 14 15 16
8 8 9 A B C D E F 10 11 12 13 14 15 16 17
9 9 A B C D E F 10 11 12 13 14 15 16 17 18
A A B C D E F 10 11 12 13 14 15 16 17 18 19
B B C D E F 10 11 12 13 14 15 16 17 18 19 1A
C C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B
D D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C
E E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D
F F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E

Пример

Для примера сложим F4240 и 7A120:

+ F 4 2 4 0
7 A 1 2 0
1 6 E 3 6 0

F424016 + 7A12016 = 16E36016

(1 000 00010 + 500 00010 = 1 500 00010)

Вычитание в шестнадцатеричной системе счисления

Правила вычитания шестнадцатеричных чисел обратны правилам сложения (см. таблицу выше).

Пример

Для примера вычтем из числа 16E360 число F4240:

– 1 6 E 3 6 0
F 4 2 4 0
7 A 1 2 0

16E36016 − F424016 = 7A12016

(1 500 00010 − 1 000 00010 = 500 00010)

Умножение чисел в шестнадцатеричной системе счисления

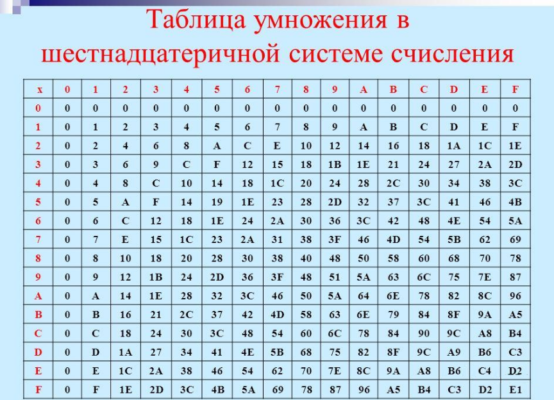
Умножение шестнадцатеричных чисел производится по следующим правилам:

× 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 A B C D E F
2 0 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E
3 0 3 6 9 C F 12 15 18 1B 1E 21 24 27 2A 2D
4 0 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C
5 0 5 A F 14 19 1E 23 28 2D 32 37 3C 41 46 4B
6 0 6 C 12 18 1E 24 2A 30 36 3C 42 48 4E 54 5A
7 0 7 E 15 1C 23 2A 31 38 3F 46 4D 54 5B 62 69
8 0 8 10 18 20 28 30 38 40 48 50 58 60 68 70 78
9 0 9 12 1B 24 2D 36 3F 48 51 5A 63 6C 75 7E 87
A 0 A 14 1E 28 32 3C 46 50 5A 64 6E 78 82 8C 96
B 0 B 16 21 2C 37 42 4D 58 63 6E 79 84 8F 9A A5
C 0 C 18 24 30 3C 48 54 60 6C 78 84 90 9C A8 B4
D 0 D 1A 27 34 41 4E 5B 68 75 82 8F 9C A9 B6 C3
E 0 E 1C 2A 38 46 54 62 70 7E 8C 9A A8 B6 C4 D2
F 0 F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2 E1

Пример

Для примера перемножим числа 1F4 и 2D:

× 1 F 4
2 D
+ 1 9 6 4
3 E 8
5 7 E 4

1F416 × 2D16 = 57E416

(50010 × 4510 = 2250010)

Деление шестнадцатеричных чисел

Деление шестнадцатеричных чисел выполняется по тому же принципу, что и деление десятичных, например:

Пример

Для примера разделим число 7D0 на 2:

Деление восьмеричных чисел

7D016 ÷ 216 = 3E816

(200010 ÷ 210 = 100010)

См. также

Источник

Шестнадцатеричная арифметика

12.03.2009
127013
Пишу
40 комментариев

компьютерная теория

Дорогие друзья, спасибо всем, кто отписался в этой статье. Откровенно говоря, когда я её писал, то не задумывался о том, что она будет так популярна (самая популярная статья на этом сайте). Видимо в самом деле стоит дописать её, чтобы полнее осветить тему. Какие-то куски старой статьи останутся здесь без изменения, что-то я дополню, еще что-то — перепишу. Итак, приступим.

Как перевести шестнадцатеричное число в десятичное?

Всё не так страшно, как может показаться в самом начале, и начнем мы с привычной всем нам десятичной арифметики. Во втором классе средней школы нас учили, например, что число 136, это — 100 + 30 + 6.

Десятичная система счисления является позиционной, так как цифры в числах (разряды) обозначают разные величины в зависимости от того, в каком месте они находятся. Поясню примером: В числе 1375 цифра 3 обозначает три сотни, так как стоит в третьей позиции или разряде; а в числе 136 из предыдущего примера тройка — это лишь три десятка, так как стоит она во втором разряде. Цифра 3 в этих примерах обозначает разные числа, так как находится в разных разрядах. Полезно вспомнить три основных правила:

  1. В десятичной системе счисления всего десять цифр (чисел, записываемых одним символом) — от 0 до 9.
  2. Число десять — первое число, которое нельзя записать одной цифрой.
  3. Число десять является основанием десятичной системы счисления.

Поясню эти правила. С первым всё понятно. Второе: действительно, когда все числа из одной цифры исчерпаны, принято составлять числа из двух и более знаков (цифр): 10, 11, 12 и т. д. Чтобы проиллюстрировать третье правило, давайте вспомним о степенях — это сведения математики пятого класса средней школы. Чтобы возвести число А в степень х, необходимо число А умножить само на себя и множителей должно быть x штук. При этом А называется основанием степени, а х — показателем, записывается как Ах Вспомним ещё одно правило: любое число А в нулевой степени равно единице, то есть А0 = 1.

Теперь вернемся к нашему первому примеру — числу 136. Используя только что восстановленные в сознании правила, его можно записать так: 136 = 100 + 30 + 6 = 1×102 + 3×101 + 6×100.

Разряды чисел принято нумеровать справа налево и начинать при этом с нуля. Эти числа соответствуют показателям степеней, в которые надо возвести десятку в только что показанной записи. Приведем еще один пример — число 1375: 1375 = 1000 + 300 +70 + 5 = 1×103 + 3×102 + 7×101 + 5×100.

Понятно, что таким способом можно расписать любое целое десятичное число.

Настало время перейти к шестнадцатеричной системе счисления. Она тоже является позиционной, то есть цифры означают в ней разные числа в зависимости от разряда, в котором находятся. Шестнадцатеричная арифметика тоже подчиняется трём правилам, но они немного изменены для неё.

  1. В шестнадцатеричной системе счисления 16 цифр (чисел, которые можно записать одним символом). Это цифры от 0 до 9 и первые шесть символов латинского алфавита — A, B, C, D, E, F. Можно при записи использовать и прописные буквы a, b, c, d, e, f. Все эти цифры соответствуют десятичным числам от нуля до 15.
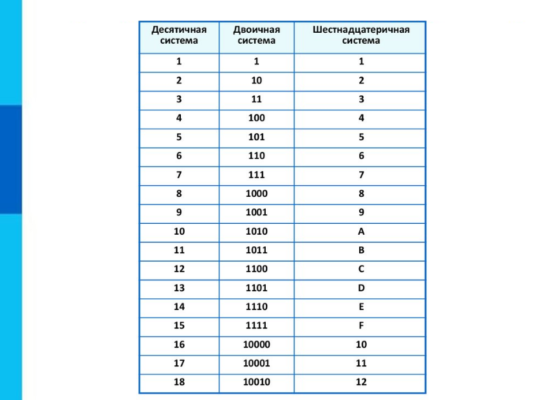
  2. Число, которое соответствует десятичному 16 — первое, которое нельзя записать одной цифрой. Проиллюстрируем это рядами чисел:

Таблица 1. Соответствие десятичных чисел шестнадцатеричным

Десятичные 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Шестнадцатеричные 0 1 2 3 4 5 6 7 8 9 a b c d e f 10
10-ная система 16-ная система
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 a
11 b
12 c
13 d
14 e
15 f
16 10

Из этого примера видно, что числа в шестнадцатеричной арифметике формируются по тем же правилам — когда исчерпаны все числа, состоящие из одной цифры, мы используем уже две цифры для записи чисел и т. д.

  1. Шестнадцать — основание в своей системе счисления. То есть, расписывая в ней числа, нужно в степень возводить число 16, а не десятку, как мы привыкли. Это, кстати говоря, позволит нам узнать, чему равно то или иное шестнадцатеричное число.

Как, например, понять, чему равно шестнадцатеричное число FF? Распишем его по известному нам правилу. Вместо десятки подставим 16, а шестнадцатеричную цифру F заменим соответствующим ей десятичным числом 15. Итак: FF = F×161 + F×160 = 15×161 + 15×160 = 15×16 + 15 = 255.

Попробуем с другим числом, например, 1F5: 1F5 = 1×162 + F×161 + 5×160 = 162 + 15×16 + 5 = 501.

Подобная запись является правилом перевода шестнадцатеричных чисел в привычные нам десятичные. А можно ли десятичное число перевести в шестнадцатеричное? Конечно, да. Но, чтобы избежать путаницы, будем десятичные числа писать как прежде, а перед шестнадцатеричными числами будем ставить префикс «0x», что повсеместно принято для записи таких чисел в компьютере.

Как перевести десятичное число в шестнадцатеричное?

Чтобы перевести десятичное число в шестнадцатеричное, необходимо выполнить следующие действия:

  1. Проверяем, не меньше ли 16 наше число: если да, то результат достигнут. Действительно, такое десятичное число необходимо лишь заменить соответствующей ему шестнадцатеричной цифрой из таблицы 1. Если же наше десятичное число больше 16, переходим к шагу 2.
  2. Делим наше число НАЦЕЛО на 16 и запоминаем целочисленный остаток от этого деления. Результат этого деления снова сравниваем с 16. Если результат деления меньше 16, то его стоит тоже запомнить как последний из остатков.
  3. Шаг 2 повторяем до тех пор, пока результат деления не будет меньше 16. Целочисленные остатки на всех этапах запоминаем. Они понадобятся в шаге 4.
  4. Все остатки записываем в обратном порядке и заменяем в них числа от 10 до 15 шестнадцатеричными цифрами от a до f.

Проиллюстрируем эти правила примером.

Переведем десятичное число 89 в шестнадцатеричное. Оно больше 16, поэтому разделим его на 16. Частное равно 5 и 9 в остатке. 5 меньше 16, значит, деление прекращается и 5 запомним как последний остаток. То есть у нас есть два остатка: 9 и 5. Теперь их надо записать в обратном порядке, получаем: 89 = 0×59.

Проверим, действительно ли 0×59 равно 89? Распишем его по привычной уже схеме: 0×59 = 5×161 + 9×160 = 5×16 + 9 = 89.

Действительно, получилось. Но в выбранном мной примере число 89 очень быстро закончилось, если так можно сказать. В противном случае деление потребовалось бы продолжить. Покажем это на более сложном примере. Возьмем число 3728: 3728 / 16 = 233 и 0 в остатке. Затем 233 / 16 = 14 и 9 в остатке. Результат этого деления равен 14, он меньше 16. Деление заканчиваем и запоминаем этот результат деления как последний остаток. Нам осталось лишь записать эти остатки в обратном порядке и заменить десятичное число 14 на шестнадцатеричную цифру E. Итак, искомое число 0xE90.

В качестве домашнего задания можете перевести это число в десятичное и проверить, действительно ли 0xE90 равно 3728?

На этом месте статья заканчивалась, я решил ее несколько дополнить. Продолжаем.

Сложение шестнадцатеричных чисел

Сначала немного поговорим о правилах. Самое первое — всегда стоит помнить о том, что шестнадцатеричная система счисления позиционная. Об этом я писал в самом начале, но не грех и повторить. Просто из этого правила следует очень важный момент, складывая числа, нужно делать это только с цифрами, находящимися в одинаковых разрядах.

Сначала мы с вами вспомним как складывать числа в столбик в привычной нам десятичной системе счисления и применим эти знания на шестнадцатеричные числа. Всего делов-то! :)

Предположим, нам необходимо сложить числа 234 и 49. Для этого мы запишем эти числа одно под другим так, чтобы разряды в них совпадали — единицы под единицами, десятки под десятками и так далее. И складывать будем цифры из одинаковых разрядов, начиная с единиц и идя влево.

Помня о том, что мы пока складываем десятичные числа (10 является основанием системы счисления), складываем разряды по очереди справа налево. 4 + 9 = 13. Наш результат — 13, он больше 10 — нашего основания. В случае, когда результат больше или равен основанию, это самое основание нужно вычесть из результата. В нашем примере от 13 необходимо отнять 10, а новый результат записать под цифрами 4 и 9, отнятую же здесь десятку, перенести в левый разряд как единицу старшего разряда (десять единиц равно одному десятку). В разряде с десятков мы складываем 3 + 4 и добавляем к ним перенесенный 1 десяток. Результат — 8. Он меньше нашего основания, значит под десятками просто записываем 8. Далее складываем сотни. Но двойку не с чем складывать, значит просто переносим ее в результат. Итак: 234 + 49 = 283.

Ровно те же правила сложения чисел действуют в любой позиционной системе счисления. Единственное отличие заключается в том, что результаты сложения цифр в разрядах придется сравнивать с другими основаниями систем счисления.

Переходим к шестнадцатеричным числам. Вспомним, что основание здесь равно 16. И неприятной особенностью являются цифры обозначенные буквами латинского алфавита. Чтобы нам было проще складывать, вспомним, чему они равны:

a = 10, b = 11, c = 12, d = 13, e = 14, f = 15.

Переходим собственно к примеру на сложение. Давайте сложим 0xA15 и 0xBC.

Сначала складываем единицы — 5 + С. Вспоминаем, что с = 12, получаем 5 + 12 = 17. Результат больше основания системы счисления, который равен 16. Значит вычитаем 16 из 17 — равно 1, записываем этот новый результат под правым разрядом, а в левый старший разряд переносим единичку (16 единиц равно одному десятку в шестнадцатеричной системе). Там же складываем 1 + B. Добавляем к этой сумме 1 перенесенный разряд и вспоминаем, что B = 11, получаем: 1 + 1 + 11 = 13. Во-первых: этот результат меньше 16, значит его можно просто записать под складываемыми цифрами, а во-вторых: Число 13 в шестнадцатеричной арифметике записывается буквой D. В разряд сотен при этом ничего не переносится, а цифра A из верхнего слагаемого просто переносится в результат. Несложно заметить, что 0xA15 + 0xBC = 0xAD1.

Вычитание шестнадцатеричных чисел

Начнем мы снова с привычной нам десятичной системы счисления. Давайте решим пример: 123-85.

Вычитание снова происходит поразрядно, но переносы делаются на сей раз слева направо. Поясню. В нашем примере необходимо из 3 отнять 5. Этого сделать нельзя, поэтому мы занимаем один десяток из левого разряда. Теперь 5 нужно отнять от 13. В результате мы получим 8, запишем этот результат под разрядом единиц. От десятков в уменьшаемом (число 123) мы один десяток заняли в разряд единиц. Теперь здесь только 1 десяток. Нам нужно из одного вычесть 8. Для этого снова приходится занять единицу из левого разряда (теперь уже сотен). Значит нужно из 11 вычесть 8. В результате получаем – 3 и записываем его под разрядом десятков. А единственную сотню мы заняли для вычитания десятков. Пример решён: 123-85 = 38.

Перейдем к вычитанию шестнадцатеричных чисел. Все делается аналогично, надо только помнить, что в случае необходимости из левых разрядов мы будем занимать не 10, а 16. Ну и снова вспомним, чему равны цифры старше девятки:

a = 10, b = 11, c = 12, d = 13, e = 14, f = 15.

Давайте решим пример 0xBC4-0xAF.

Из 4 нельзя вычесть F, значит из левого разряда мы займем 16. Теперь F надо вычитать из 20. В результате — 5, записываем его под разрядом единиц. Цифра C уменьшилась на 1, теперь это B. Значит надо A вычесть из B. Нетрудно догадаться, что в результате будет 1. Записываем этот результат в разряде десятков. Из сотен в этот раз мы ничего не занимали и в вычитаемом только 2 цифры — сотен нет, то есть сносим B из уменьшаемого в результат. Итак: 0xBC4-0xAF = 0xB15, пример решен. Было ли сложно? :)

Теги раздела

css (1), wordpress (4), изыски словообразования (4), компьютерная теория (9), компьютерный практикум (5), кулинария (1), мобильная связь (1), мои университеты (2), облако тегов (1), проза (33), рифмы (4), свои функции (1), теле2 (1), фельетон (1), шрифты (1), эссе (1), юмор (8)

Оставьте ваш отзыв:

Источник

Шестнадцатиричная система счисления


Шестнадцатиричная система счисления

4.1

Средняя оценка: 4.1

Всего получено оценок: 202.

4.1

Средняя оценка: 4.1

Всего получено оценок: 202.

Для записи адресов и содержимого ячеек памяти компьютера используется шестнадцатеричная система счисления. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение арифметических операций над ними имеет ряд особенностей, о чем можно прочитать в данной статье.

Что такое шестнадцатеричная система счисления

Шестнадцатеричная система счисления использует для записи числовых значений шестнадцать символов: арабские цифры от 0 до 9 и буквы латинского алфавита A, B, C, D, E, F. Соответственно, основанием такой системы счисления будет число 16.

При использовании шестнадцатеричных чисел следует помнить, что в числовом ряду шестнадцатеричных чисел после числа 9 идет А, а после F следует двузначное число 10.

Перевод 16 –10

Для прямого перевода шестнадцатеричного числа в десятичную систему удобно пользоваться развернутой формой записи, когда число представляют в виде суммы, в которой слагаемые получаются путем умножения символа разряда (числа или числового эквивалента буквы) на 16 в степени соответствующего разряда.

Например, 1F4 = 1 * (16^2) + 15 * (16^1) + 4 * (16^0) = 256 + 240 + 4 = 500

Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.

Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.

Например: 500 / 16 = 31 (остаток 4)

31 / 16 = 1 (остаток 15 заменяем на букву F)

Таким образом, получено шестнадцатеричное число 1F4.

Перевод 16 – 2

Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.

Рис. 1. Таблица соответствия шестнадцатеричных чисел и их двоичных и десятичных эквивалентов

Например, 1F4 = (0001)(1111)(0100).

Арифметические действия в шестнадцатеричной системе счисления

Сложение и вычитание

Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.

Рис. 2. Таблица сложения шестнадцатеричных чисел

Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.

Например, 1F + 2D = 4C.

Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.

Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.

Таким образом, получается число 4C.

При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.

Например, 2D – 1F = E.

Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.

После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.

Умножение и деление

Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.

Рис. 3. Таблица умножения шестнадцатеричных чисел

Например, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38

Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.

Заключение

Что мы узнали?

В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда — пройдите тест.

  • Роман Журавлев

    10/10

  • Татьяна Лазарева

    10/10

  • Коля Приходько

    8/10

  • Андрей Букин

    10/10

  • Игорь Карабута

    1/10

  • Александра Цалко

    8/10

Оценка статьи

4.1

Средняя оценка: 4.1

Всего получено оценок: 202.

А какая ваша оценка?

Источник

In the hexadecimal number system, the numbers are expressed with the base 16. Hexadecimal is also called as Hex. It is like decimal, binary or octal numbers. The list of 16 hexadecimal numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Here, we are going to learn how to perform addition, subtraction operations in between two hexadecimal numbers with the examples for the better understanding of the concept. So, interested people can check out this complete page.

What is Hexadecimal Number System?

A hexadecimal number is a number having a base of 16. These numbers are also called the 16 number system. It has 16 different symbols, 0 to 9 represent the binary values, A, B, C, D, E, F represent 10 to 15 values respectively. Each position in the hexadecimal number represents 0 power of the base 16. The last position in the number represents an x power of base 16.

Examples of Hexadecimal Numbers:

1. B84F

The decimal value of B84F is 11 x 16 + 8 x 16 + 4 x 16 + 16 x 16

= 176 + 128 + 64 + 256

= 624

2. Convert 857 to hexadecimal

857 ÷ 16 = 53.5625

0.5625 x 16 = 9 (Remainder 9)

53 ÷ 16 = 3.3125

0.3125 x 16 = 5 (Remainder 5)

3 ÷ 16 = 0.1875

0.1875 x 16 = 3 (Remainder 3)

Read remainders from bottom to top

So, 857 = (359)16

Also, Read: Binary Subtraction

Procedure for Adding & Subtracting in Hexadecimal

Below provided are the simple steps that are helpful to compute the addtion and subtraction of two hexadecimal numbers.

1. Hexadecimal Numbers Addition

  • Write two hexadecimal numbers one after another in two different lines
  • Begin adding from the rightmost digits.
  • If the digit is in the form of an alphabet then convert it to the respective decimal number to make the process easy
  • Add those digits and convert the sum to the hexadecimal
  • If you got the carry, then represent it on the top of the first number next digit and result on the bottom of the second number added digit.
  • Continue the process until you left nothing on the left side.

We can also add two hexadecimal numbers by following this table.

Hexadecimal Addition and Subtraction

For Example:

926 + 1A2

9 2 6

(+) 1 A 2

=    A C 8

So, 926 + 1A2 = AC8

2. Hexadecimal Numbers Subtraction

  • Write two hexadecimal numbers in different lines
  • Subtraction starts from the rightmost digits of the numbers.
  • Convert the alphabets into decimals and subtract two digits and again convert the difference value as hexadecimal.
  • In case the first number digit is smaller than the second number digit, then barrow from the left side digit.
  • The borrowed value is always 16 as its base is 16. Then add borrowed value and first number digit and subtract.
  • Don’t forget to mention the borrowed value on the top of the first number digit.
  • After borrowing, the left side digit decreased by 1.
  • Repeat the process till you have nothing remaining on the left side.

For Example:

938 – 1A2

8 – 2 = 6

3 – A(10) = (16 + 3) – 10 = 19 – 10 = 9

(9 – 1) – 1 = 8 – 1 = 7

So,  938 – 1A2 = 796.

Hexadecimal Addition and Subtraction Examples

Example 1:

Evaluate (1AB2)16 + (2198)16

Solution:

Given expression is (1AB2)16 + (2198)16

From the table,

2 + 8 = A

B + 9 = 4 and 1 is carry

1 + A + 1 = C

1 + 2 = 3

Therefore, (1AB2)16 + (2198)16 = 3C4A

Example 2:

Find subtraction of (B84F)16 and (A53)16.

Solution:

F means 15. F – 3 = 15 – 3 = 12 = C

4 + 16 = 20 – 5 = 15 = F

8 – 1 = 7

7 + 16 = 23 – A = 23 – 10 = 13 = D

8 – 1 = 7
23
10 7 20

B 8 4 F

(-) 0 A 5 3

= 7 D F C

So, (B84F)16 – (A53)16 = (7DFC)16

Example 3:

Find the addition, subtraction of (AB53)16, (155)16

Solution:

The addition of numbers is (AB53)16 + (155)16

3 + 5 = 8

5 + 5 = 10 = A

B + 1 = 11 + 1 = 12 = C

A + 0 = 10 + 0 = 10 = A

So, (AB53)16 + (155)16 = (ACA8)16

Subtraction of numbers is (AB53)16 – (155)16

(3 + 16) – 5 = 19 – 5 = 14 = E

(5 – 1) – 5 = 4 – 5

(4 + 16) – 5 = 20 – 5 = 15 = F

(B – 1) – 1 = (11 – 1) – 1 = 10 – 1 = 9

A – 0 = A

A B 5 3

(-) 0 1 5 5

= A 9 F E

So, (AB53)16 – (155)16 = (A9FE)16

Example 4:

(i) Calculate (9AB)16 + (12C)16

(ii) Compute (CB5)16 – (223)16

Solution:

(i) (9AB)16 + (12C)16

B + C = 11 + 12 = 23 = 7 and 1 is carry

1 + A + 2 = 3 + 10 = 13 = D

9 + 1 = 10 = A

So, (9AB)16 + (12C)16 = (AD7)16

(ii) (CB5)16 – (223)16

5 – 3 = 2

B – 2 = 11 – 2 = 9

C – 2 = 12 – 2 = A

So, (CB5)16 – (223)16 = (A92)16

Источник

  1. Действия с шестнадцатеричными числами.

    1. Сложение шестнадцатеричных чисел.

При сложении
шестнадцатеричных чисел следует помнить,
что

Сложение
шестнадцатеричных чисел проводят
столбиком. Сложение удобно проводить
в десятичной системе, переводя результат
в шестнадцатеричную. Если получено
число больше

,
то из него вычитают

,
прибавляя единицу к старшему разряду.

Пример:

Считаем справа
налево:


  • ;


  • ;


  • ;


  • ;


  • ,
    единица переходит в старший разряд;

  • + единица из
    предыдущего разряда

    .

    1. Вычитание шестнадцатеричных чисел.

Вычитание
шестнадцатеричных чисел удобно проводить
столбиком. Если нужно отнять от меньшего
числа большее, занимаем единицу в старшем
разряде. В младший разряд она приходит
как десятичное

(шестнадцатеричное

).
Если имеются промежуточные разряды
(содержащие нули), в них остаётся
десятичное

(шестнадцатеричное

).

Пример:

Считаем справа
налево:

Сложение
отрицательных чисел и чисел с разными
знаками осуществляется так же, как
и для двоичных чисел (см. выше, стр. 8).

4. Перевод чисел из десятичной системы счисления в другие системы

  1. Перевод целых десятичных чисел в другие системы счисления.

Алгоритм
перевода

    1. Делят
      данное десятичное число на основание
      системы счисления, в которую следует
      перевести это число.

    2. Переводят
      остаток от деления в новую систему
      счисления. Это будет младший разряд
      нового числа.

    3. Если
      частное от деления не меньше основания
      новой системы счисления, то продолжают
      деление, как указано в п.1. Следующий
      остаток, переведенный в новую систему
      счисления, даёт второй разряд числа и
      т.д.

    4. Старший
      разряд нового числа равен последнему
      частному от деления, меньшему основания
      новой системы счисления.

В качестве примера,
переведем число 189 из десятичной в
двоичную, восьмеричную и шестнадцатеричную
системы счисления2.

3


189

2

188

94

2

1

94

47

2

0

46

23

2

1

22

11

2

1

10

5

2

1

4

2

2

1

2

1

0

1
89

8

184

23

8

5

16

2

7


4

1
89

16

176

11

13

B

D

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти машину зная водителя
  • Как найти кнопка пуск
  • Как найти вторую девушку парня
  • Как найти сонар в гта 5
  • Как составить счет на задолженность