|
Как проверить, существует ли треугольник, если известны три его стороны? Необходимым и достаточным условием существования треугольника является выполнение следующих неравенств: a+b>c, a+c>b, b+c>a, (a>0, b>0, c>0), где a, b и с — длины сторон треугольника. Другими словами, треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны. автор вопроса выбрал этот ответ лучшим Kuzmich291192 9 лет назад Условие существования треугольника можно представить в следующем виде: пусть a b c стороны треугольника. Тогда, что бы треугольник существовал необходимо, что бы сумма двух любых его сторон была больше третьей стороны a+b>c или a+c>b или b+c>a (если сумма будет равна какой-либо стороне, то такой треугольник называется вырожденным). Рассмотрим пример: пусть дан треугольник со сторонами 3, 6, 5. Возьмём две любые стороны, например, 3 и 6. Проверим условие существования: 3+6=9>5, следовательно треугольник существует. Так же условие сущесвтвования треугольника можно представить в виде векторной суммы. Пусть вектора a b c задают стороны треугольника(и эти вектора не равны нуль-вектору), тогда треугольник существует, если векторная сумма a+b+c=0. Mefody66 9 лет назад Kuzmich291192 написал в общем, все правильно, но с одним маленьким уточнением: нужно взять самую большую сторону, и проверить, что сумма двух других сторон больше, чем эта большая сторона. Возьмем, например, числа 1, 2 и 10. Если мы сложим 1 + 10 > 2, 2 + 10 > 1, значит, треугольник существует? НЕТ! 1 + 2 < 10. Поэтому треугольник не существует. У м к а 6 лет назад В геометрии есть теорема под названием «Неравенство треугольника», которая гласит о том, что любая из сторон треугольника не будет превосходить по своему значению сумму двух других его сторон. Примечательно, что данная теорема также имеет доказательство. Таким образом, вам необходимо всего лишь поочерёдно просуммировать по две стороны треугольника и сравнить полученное значение с размером третьей стороны, которая не участвовала с сложении. Galina7v7 4 года назад Когда такой вопрос конкретно задаётся, причём, в цифрах, то нужно проверить величину каждой стороны, чтобы на была меньше суммы двух других сторон. Вот треугольник со сторонами 3,4, и 5 существует, а изменив только одну из сторон, например, 5 см на 7 см, то такого треугольника не существует, так 3 + 4 = 7, а не больше, как положено для существования треугольника. Начинать проверку нужно для большей стороны, и если она меньше суммы двух меньших сторон, то этот треугольник существует. Требование к углам треугольника тоже не маловажное, потому что если даны углы треугольника, и сумма их не равна 180 градусам, то треугольник не существует. Если известны длины трех сторон треугольника, то еще до его построения можно определить может ли такой треугольник существовать реально. Есть даже простенькая программа для вычисления этого на компьютере, но все что нам надо это найти самую длинную сторону из заданных и проверить является ли сумма двух других сторон больше. Примерно так: заданы три сторона а, в, с, причем в сторона самая длинная. Условием возможности существования треугольника будет выполнение неравенства в<а+с. Если большая сторона будет равна сумме двух других сторон, то это случай вырожденного треугольника, когда все вершины лежат на одной прямой: Azamatik 6 лет назад Имеем треугольник АВС, где АВ, ВС и СА — это три его стороны. Треугольник существует в тех случаях, когда АВ + ВС > СА; АВ + СА > ВС; ВС + СА > АВ, то есть в том случае, если сложить любые две стороны любого треугольника, сумма должна быть больше третьей его стороны. Например, АВ = 5 см, ВС = 6 см, СА = 8 см – треугольник существует. И другой пример: АВ = 4 см, ВС = 3 см, СА = 9 см. Получается, что одна сторона больше суммы двух других — треугольник не существует. moreljuba 6 лет назад Чтобы проверить существование треугольника нужно сложить все три угла треугольника ивот если они в сумме не дадут 180-ти градусов, то такого треугольника просто как раз не существует. А также треугольника не существует в том случае, когда одна сторона будет по длине больше чем длина в сумме двух других сторон. Помощни к 6 лет назад Если одна из сторон треугольника будет больше (по длине), чем две других стороны, то из этих катетов не получится сделать один треугольник. Получится фигура, напоминающая флажок, состоящая из треугольника и присоединенной линии. Любая сторона не может быть больше сумму двух оставшихся сторон треугольника. Smiledimasik 6 лет назад Самое главное во всех правилах существования треугольника то, что сума двух меньших сторон треугольника или как называются они «катеты» должна быть больше самой большой стороны треугольника. Если сума этих сторон совпадет с самой большой стороной, то это будет обычная прямая с точками на ней. MarkTolkien 6 лет назад Длина каждой из сторон треугольника должна быть меньше сумы остальных двух сторон, иначе этот треугольник не сложится. Углы треугольника в сумме дают 180 градусов, это еще один критерий для проверки, позволяющий вычислить, существует ли треугольник. Roxrite 9 лет назад Если одна сторона треугольника окажется больше суммы двух остальных сторон, то такого треугольника не существует. Если сумма всех 3-х углов треугольника не будет равна 180°, то такого треугольника не существует. Знаете ответ? |
Существующие треугольники

Обновлено 28.02.2022
Содержание
- Определение
- Теорема
- Доказательство теоремы
- Следствия из теоремы
- Признаки существования треугольника
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
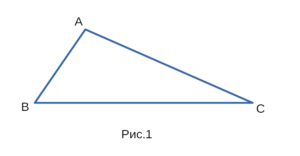
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
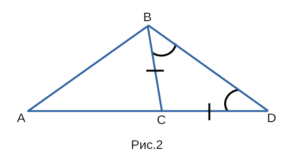
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠CBD = ∠CDB.
- Рассмотрим △ABD: ∠ABD > ∠CBD, следовательно ∠ABD > ∠CDB, то AB < AD.
- Но AD = AC + CD = AC + CB, поэтому AB < AC + CB, ч.т.д.
Следствия из теоремы
- Для любых точек А, В, С, не лежащих на
одной прямой справедливы неравенства:
AB < AC + BC
AC < AB + BC
BC < AC + AB
- Каждая сторона треугольника меньше суммы двух других сторон.
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним углов.
- Теорема о неравенстве треугольника для разности сторон.
Признаки существования треугольника
- Если каждая сторона треугольника меньше суммы двух других сторон, значит треугольник существует.
- Если большая сторона треугольника меньше суммы двух других сторон,
значит треугольник существует. - Если сумма углов треугольника равна 180°, значит треугольник существует.
Онлайн калькулятор поможет проверить существование треугольника.
Чтобы треугольник существовал, сумма двух сторон треугольника всегда должна быть больше третей стороны.
a + b > c, b + c > a, a + c > b.
Определить существование треугольника |
|
| Сторона треугольника A | |
| Сторона треугольника B | |
| Сторона треугольника C | |
|
|
|
Скачать калькулятор
Рейтинг: 3.4 (Голосов 78)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Сторона квадрата |
| Стороны ромба | Стороны параллелограмма | Ребро куба | Боковое ребро параллелепипеда |
Определить существование треугольника по трем сторонам
С клавиатуры вводятся длины трех отрезков. Определить, можно ли из них составить треугольник.
Решение задачи на языке программирования Python
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b, b + c, a + c. Первую сумму сравниваем с оставшейся стороной c, вторую — с a и третью — с b. Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
print("Стороны:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) if a + b > c and a + c > b and b + c > a: print("Треугольник существует") else: print("Треугольник не существует")
Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:
print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) flag = '' if a + b > c: if a + c > b: if b + c > a: print("Треугольник есть") else: flag = 'a' else: flag = 'b' else: flag = 'c' if flag != '': print("Треугольника нет") print("'%s' > суммы других" % flag)
Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует.
Пример выполнения программы:
Длины сторон треугольника: a = 4 b = 5 c = 10 Треугольника нет 'c' > суммы других
Более изящным решением является использование оператора множественного ветвления языка программирования Python: if-elif-else.
print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) flag = '' if a + b <= c: flag = 'c' elif a + c <= b: flag = 'b' elif b + c <= a: flag = 'a' else: print("Треугольник есть") if flag != '': print("Треугольника нет") print("'%s' > суммы других" % flag)
Здесь сравнение происходит от обратного: утверждается, что сумма двух сторон меньше или равна третьей. Если это так (утверждение верно), то треугольника не существует. «Слишком длинная сторона» определяется в зависимости от того, в заголовке какой ветки логическое выражение возвращает истину.
Больше задач в PDF
Как проверить существует ли треугольник с данными сторонами?
Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.
Как определить какой вид треугольника?
В зависимости от углов треугольник может быть:
- Прямоугольным , если один из углов равен 90 градусов;
- Тупоугольный , если один из углов тупой, т. е. больше 90 градусов;
- Остроугольным , если все углы треугольника острые.
28 нояб. 2021 г.
Когда можно сделать треугольник?
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Как определить Невырожденный треугольник?
По заданным длинам трех отрезков определить, можно ли из них составить невырожденный треугольник. Треугольник называется невырожденным, если его площадь больше 0.
Как узнать существует ли треугольник?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Как называется треугольник со сторонами 3 4 5?
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Как это Тупоугольный треугольник?
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т. е. один из его углов лежит в пределах между 90° и 180°.
Как доказать что треугольник тупой?
Тупоугольным называется треугольник, в котором
- один из углов больше 90 градусов
- есть две одинаковые стороны
- один из углов равняется 90 градусов
- есть острый угол
11 янв. 2021 г.
Почему не существует треугольника со сторонами 124?
1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.
Когда треугольник является Остроугольным?
Остроугольный треугольник – это треугольник, в котором все три угла острые, т. е. меньше 90°. Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.
Как проверить можно ли построить треугольник?
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Какая фигура называется треугольником?
Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Как называется треугольник со сторонами?
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Равносторонним или правильным называется треугольник, у которого все три стороны равны.
Как называется равносторонний треугольник?
Треугольник, все стороны которого равны, называется равносторонним.
Что такое элемент треугольника?
Треугольником называют многоугольник с тремя сторонами и тремя углами. Основными элементами данной геометрической фигуры являются отрезки, вершины и углы.
Когда треугольник Тупоугольный?
Тупоугольный треугольник. В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника. Рис.
Как определить является ли треугольник Остроугольным?
Определить треугольник тупоугольные — один из углов более 90 градусов, прямоугольные — один из угол равен 90 градусов, остроугольные — все углы менее 90 градусов.