Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
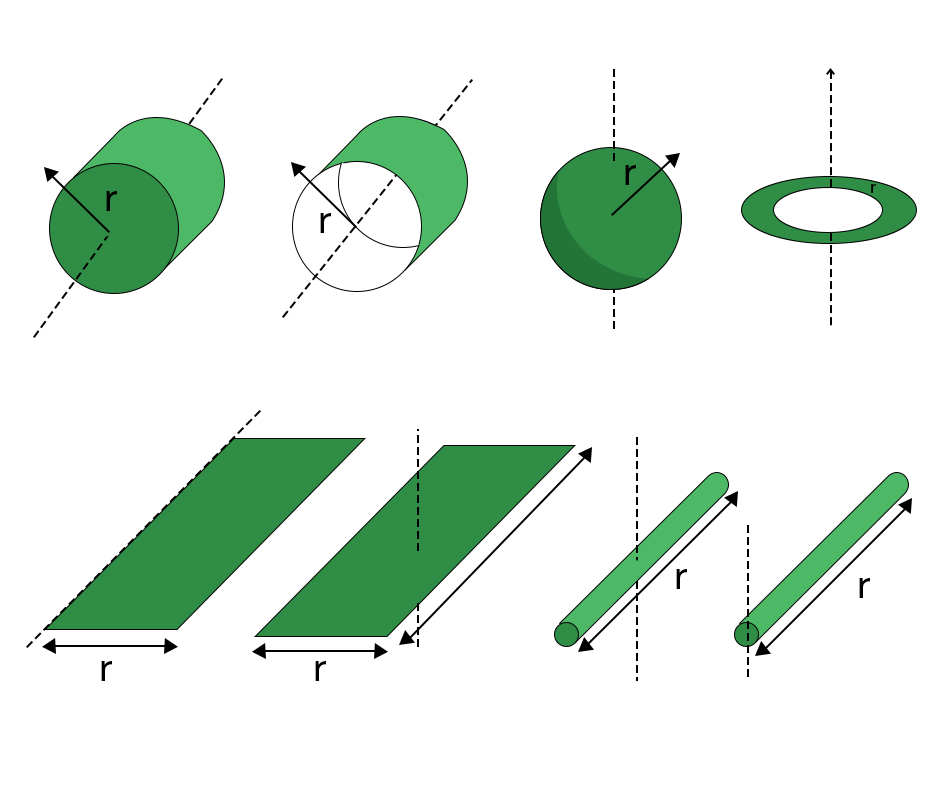
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
The moment of inertia, referred to as the angular mass or rotational inertia, with respect to the rotation axis is a quantity that determines the amount of torque necessary to achieve a desired angular acceleration or a characteristic of a body that prevents angular acceleration. The moment of inertia is calculated as the sum of each particle’s mass times the square of its distance from the rotational axis.
Moment of Inertia
The term “moment of inertia” refers to the quantity that describes how a body resists angular acceleration and is calculated as the product of the mass of each particle times the square of the particle’s distance from the rotational axis. Or, to put it another way, you could say that it’s a quantity that determines how much torque is required for a certain angular acceleration in a rotating axis. Inertia moment is often referred to as rotational inertia or angular mass. kg m2 is the unit of moment of inertia in the SI system.
Moment of Inertia of a System of n Particles
The moment of inertia is the following for a system of point particles rotating around a fixed axis:
I = ∑miri2
where,
ri is the distance between the axis and the ith particle,
mi is the mass of ith particle.
How to Calculate Moment Of Inertia?
Several ways are used to calculate the moment of inertia of any rotating object.
- For uniform objects, the moment of inertia is calculated by taking the product of its mass with the square of its distance from the axis of rotation (r2).
- For non-uniform objects, we calculate the moment of inertia by taking the sum of the product of individual point masses at each different radius for this the formula used is
I = ∑miri2
Formulas For Calculating Moment Of Inertia
Expressions for the moment of inertia for some symmetric objects along with their axis of rotation are discussed below in this table.
| Object | Axis | Expression of the Moment of Inertia |
|---|---|---|
| Hollow Cylinder Thin-walled | Central | I = Mr2 |
| Thin Ring | Diameter | I = 1/2 Mr2 |
| Annular Ring or Hollow Cylinder | Central | I = 1/2 M(r22 + r12) |
| Solid Cylinder | Central | I = 1/2 Mr2 |
| Uniform Disc | Diameter | I = 1/4 Mr2 |
| Hollow Sphere | Central | I = 2/3 Mr2 |
| Solid Sphere | Central | I = 2/5 Mr2 |
| Uniform Symmetric Spherical Shell | Central | |
| Uniform Plate or Rectangular Parallelepiped | Central | I = 1/12 M(a2 + b2) |
| Thin rod | Central | I = 1/12 Mr2 |
| Thin rod | At the End of Rod | I = 1/3 Mr2 |
Solved Examples of Moment of Inertia
Example 1: Determine the solid sphere’s moment of inertia at a mass of 22 kg and a radius of 5 m.
Answer:
Given:
M = 22 kg, R = 5 mWe have for solid sphere, MOI (I) = 2/5 MR2
I = 2/5 × 22 × 25
I = 220 kg m2
Example 2: Calculate the mass of the uniform disc when its moment of inertia is 110 kg m2 and its radius is 10 m.
Answer:
Given:
I = 110 kg m2, R = 10 mWe have for uniform disc (I) = 1/4 MR2
M = 4I / R2
M = 4 × 110 / 102
M = 440 / 100
M = 4.4 kg
Example 3: If a uniform plate has a mass of 23 kg, a length of 10 m, and a breadth of 7 m, determine its moment of inertia.
Answer:
Given: M = 23 kg, L = 10 m, b = 7 m
We have for uniform plate MOI


I = 285 kg m2
Example 4: When the uniform hollow right circular cone has a moment of inertia of 98 kg m2 and a mass of 20 kg, determine the radius of the cone.
Answer:
Given:
I = 98 kg m2, M = 20 kgWe have for right circular cone, MOI (I) = 1/2 MR2
R2 = 2I / M
R2 = 2 × 98 / 20
R2 = 9.8
R = √9.8
R = 3.13 m
Example 5: If the mass is 10 kg and the radius is 7 m, determine the hollow cylinder’s moment of inertia.
Answer:
Given:
M = 10 kg, R = 7 mWe have for hollow cylinder, MOI (I) = MR2
I = 10 × 49
I = 490 kg m2
Example 6: When r1 is 10 m, r2 is 20 m, and the mass of the annular ring is 14 kg, calculate the moment of inertia of the ring.
Answer:
Given: r1 = 10 m, r2 = 20 m, M = 14 kg
We have for Annular ring (I) = 1/2 M(r22 + r12)
I = 1/2 × 14 × (400 + 100)
I = 7000 / 2
I = 3500 kg m2
Related Resources
- Mass and Inertia
- Inertia
- Rotational Inertia
Last Updated :
15 Oct, 2022
Like Article
Save Article
Когда тело продолжает двигаться при отсутствии на него воздействия каких-либо сил, говорят о проявлении инерции. Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.
Момент инерции и его физический смысл
Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.
Было понятно, что именно масса тела характеризует степень его инертности и является ее мерой.
При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.
Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.
Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:
МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.
В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.
Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила. Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.
Единицы измерения в системе СИ
Единицей измерения момента инерции, принятой в системе СИ, является кг, умноженный на метр в квадрате — кг·м². В еще одной системе измерения (СГС) единицей измерения является грамм на квадратный сантиметр — г·см².
Как рассчитать момент инерции, формула
Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.
Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.
Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.
Виды моментов инерции
Кроме безразмерного момента инерции, в физике существуют понятия:
- центробежный МИ;
- главный МИ;
- геометрический МИ;
- МИ относительно плоскости;
- центральный МИ;
- тензор инерции;
- эллипсоид инерции.
Центробежными МИ относительно прямоугольных осей координат (декартовой системы) считаются Jxy, Jxz, Jyz. Ось ОХ является главной, когда центробежные моменты инерций Jxy и Jxz равняются нулям.
Любая точка тела может являться центром трех главных осей инерции. Они характеризуются взаимной перпендикулярностью. МИ относительно них считается главным для данного предмета. Главные оси, которые пролегают через центр масс, — являются главными центральными осями инерции предмета. МИ относительно них – главные центральные МИ. Для однородного тела ось симметрии всегда является главной центральной осью инерции.
Для геометрических МИ существуют формулы, основывающиеся на объеме относительно оси и площади относительно оси.
Твердое тело может иметь МИ относительно плоскости. Тогда это – скалярная величина, которая рассчитывается суммированием произведений массы каждой точки предмета и расстояния от нее до плоскости, возведенного в квадрат.
Понятие «Центрального МИ» связано с точкой О, МИ относительно полюса либо полярным МИ.
Момент инерции тела относительно оси вращения
МИ служит единицей измерения инерции тела, которое вращается вокруг оси, подобно тому, как масса является мерой при поступательном движении.
Определить МИ предметов касательно оси вращения позволяет формула Штейнера.
Пример:
Наглядное подтверждение применения формулы Штейнера – расчет МИ стержня, ось вращения которого проходит через конец.
Моменты инерции простейших объектов
Момент инерции некоторых однородных тел, имеющих простую форму, в зависимости от характеристик осей вращения можно определить по следующим формулам:
- МИ точечного предмета либо полого цилиндра с тонкими стенками (с массой m и радиусом r) = mr2
- МИ диска или сплошного цилиндра = 1/2 mr2
- МИ цилиндра с толстыми стенками, у которого внешний радиус обозначен r2, а внутренний – r1, :
- МИ сплошного цилиндра с осью вращения, перпендикулярной образующей цилиндра, расположенной по центру масс:
- МИ полого цилиндра с тонкими стенками и осью, перпендикулярной к цилиндру и проходящей через центр масс:
- МИ прямого тонкого стержня с осью, перпендикулярной к нему и проходящей через центр масс:
- МИ сферы с тонкими стенками и осью по центру = 2/3 mr2
- МИ шара с осью по центру = 2/5 mr2
- МИ равнобедренного треугольника с осью, перпендикулярной его плоскости и проходящей через вершину:
Примеры решения задач
Применение на практике приведенных формул происходит, например, для решения следующих задач.
Пример №1
Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска.
Для решения диск разбивается на тонкие кольца, радиусы которых равняются от 0 до R. Взяв одно из них и обозначив его радиус буквой (r), а массу – (dm), формула для расчета МИ (согласно теореме Гюйгенса-Штейнера) выглядит следующим образом: (dJ=dmr2.)
С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем:
Пример № 2
Задано найти у того же диска МИ относительно оси, которая проходит через середину радиуса.
Из предшествующего задания используем найденную величину МИ относительно оси, которая проходит через центр масс. Используя формулу Штейнера, решаем задачу.
Если решать аналогичные задачи нет желания или времени, а контрольную работу нужно сдать в срок, на помощь придут сотрудники Феникс.Хелп.
Свойство любого объекта, который может вращаться.
Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси. Каждая частица в теле движется по кругу с линейной скоростью, то есть каждая частица движется с угловым ускорением.
Это свойство тела, благодаря чему оно сопротивляется угловому ускорению, которое представляет собой сумму произведений массы каждой частицы в теле на квадрат ее расстояния от оси вращения.
Обозначается момент инерции символом II (альтернативно обозначается JJ).
I=mr2I=mr^2,
где mm – масса тела, rr – расстояние от тела до оси вращения.
Момент инерции играет похожую роль в механике вращения с массой в обычной линейной механике. Действительно, момент инерции напрямую зависит от массы, а также от распределения этой массы относительно оси вращения.
Чем вращение массы тела происходит дальше от оси, тем труднее изменить скорость вращение этой системы.
Момент инерции в системе СИ измеряется в кг·м2 (килограмм умноженный на квадратный метр).
Связь момента инерции со вторым законом Ньютона
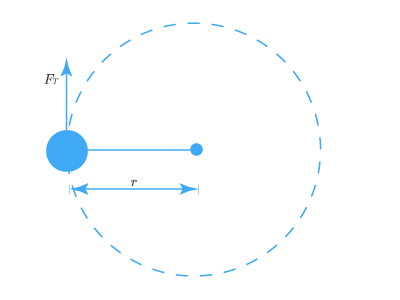
Момент инерции занимает место массы во «вращательной» версии второго закона Ньютона. Если рассмотреть массу mm, прикрепленную к одному концу стержня (для простоты объяснения массу стержня приравняем к 0). Другой конец стрежня прикреплен так, что вся система может вращаться вокруг центральной точки.
Далее система приводится во вращения, в результате действия тангенциальной силы FTFT на тело. Из второго закона Ньютона:
FT=maT или FT=m(rα)F_T = ma_T ~ или ~ F_T = m(rα)
В механике вращения крутящий момент τ=F⋅rτ = F·r занимает место силы. Умножив на rr последнее выражение, получим:
FTr=m(rα)rF_T r= m(rα) r, отсюда
τ=mr2ατ = mr^2α,
τ=Iατ = Iα
Это выражение можно использовать для определения поведения массы в ответ на действующий крутящий момент.
Момент инерции сложных фигур
Для более сложных фигур, чтобы найти момент инерции необходимо сделать несколько промежуточных вычислений. Для многих геометрических фигур существуют таблицы с уравнениями для моментов инерции. Более трудоемким будет вычисление момента инерции сложного тела, если представить его как сумму более простых тел.
Полученные моменты вращений каждого тела, объединяются в инерцию составного объекта.
Проблема, которая может возникнуть, состоит в том, что ось вращения для каждого тела будет отличаться и не будет совпадать с моментом инерции главного тела. Уравнение ниже позволяет связать момент инерции одного тела относительно момента инерции всего составного объекта:
I0=Ic+md2I_0 = I_c +md^2,
I0I_0 — момент инерции относительно точки OO (например, точка вокруг которой вращается составной главный объект), IcI_c — момент инерции относительно точки СС (например, точка вокруг которой вращается часть объекта), mm – масса части объекта, dd – расстояние между точками OO и CC.
Момент инерции важен почти во всех физических задачах, связанных с массой во вращательном движении. Он используется для расчета момента импульса и позволяет объяснить (посредством сохранения момента импульса), как изменяется вращательное движение при изменении распределения массы. А также при необходимости поиска энергии, которая хранится в виде вращательной кинетической энергии во вращающемся маховике.
Тест по теме «Момент инерции»
Момент
инерции —
скалярная
физическая величина, характеризующая
распределение масс в теле, равная сумме
произведений элементарных масс на
квадрат их расстояний до базового
множества (точки, прямой или плоскости).
Единица
измерения СИ: кг·м².
Обозначение:
I
или J.

расчета моментов
инерции
тонкого диска
массы m
и радиуса R
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним
радиусом
r
и наружным r+dr.
Площадь такого кольца ds=2r
$pi$ dr, а его
масса
,
гдеS= $pi$ R2
— площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
Вычисление
момента
инерции тонкого стержня:
Пусть
тонкий стержень имеет длину l
и массу m.
Разделим его на малые элементы длины
dx
(рис.27), масса которых
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции,
т.е.
Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
Момент
инеpции обручаотносительно оси,
пpоходящей чеpез центp кольца пеpпендикуляpно
к его плоскости. В этом случае все
элементаpные массы обруча удалены от
оси на одинаковое pасстояние, поэтому
в сумме (3.18) r2 можно вынести за знак
суммы, т. е.
Теорема
Штейнера:
В
общем случае вращения тела произвольной
формы вокруг произвольной оси, вычисление
момента инерции может быть произведено
с помощью теоремы Штейнера: момент
инерции относительно произвольной оси
равен сумме момента инерции J0 относительно
оси, параллельной данной и проходящей
через центр инерции тела, и произведения
массы тела на квадрат расстояния между
осями: J=J0+ma^2.
Например,
момент инерции диска относительно оси
О’ в соответствии с теоремой Штейнера:
17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
Линия
— ось вращения.
— масса на квадрат радиуса окружности,
по которой движется материальная точка.
Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка
.
Твердое
тело представляется как совокупность
системы точечных масс.
— расстояние, на котором находится точка
от оси вращения.
— общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
Момент
инерции шара.
Сплошной шар массы
m
и радиуса R
можно рассматривать как совокупность
бесконечно тонких сферических слоев с
массами dm
, радиусом r,
толщиной dr
(рис.35).
Рассмотрим
малый элемент сферического слоя $delta$
m с координатами
x, y, z.
Его моменты инерции относительно осей
проходящих через центр слоя — $delta$
Jx,
$delta$ Jy,
$delta$ Jz,
равны
Т.
е. можно записать
(п.26)
Так как для
элементов сферического слоя x2+y2+z2=r2
то
После
интегрирования по всему объему слоя
получим
(п.27)
Так как, в силу
симметрии для сферического слоя
dJx=dJy=dJz=dJ
, а

тоИнтегрируя по всему объему шара,
получаем
Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен
Разобьём
КОНУС
на цилиндрические слои
ось
толщиной dr.
Масса такого слоя
dm
= r2dr,
где
ρ – плотность
материала, из которого изготовлен конус.
Момент инерции этого слоя
dI = dm.r2.
Момент
инерции всего конуса
складывается
из моментов инерции всех слоёв:
I
=
=
ρπ
r
4
dr
=
ρR5.
Остаётся выразить
его через массу всего цилиндра:
m
=
=
=
R3,
отсюда ρ
=
,
I
=
=
mR2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #