Определение
8. Векторы
называются компланарными,
если их можно отложить в одной плоскости.
Свойства
компланарных векторов.
10.
Коллинеарные векторы компланарны. Иными
словами, во множество всех возможных
компланарных между собой векторов
вместе с каждым его вектором входят все
векторы, коллинеарные с ним. В частности,
нулевой вектор содержится в любом таком
множестве и вместе с каждым вектором в
это множество входит противоположный
ему вектор. Отсюда же следует, что
множество компланарных векторов замкнуто
относительно операции умножения на
действительное число.
20.
Сумма двух векторов есть вектор,
компланарный с ними. Следовательно,
множество компланарных векторов замкнуто
относительно операции сложения.
30.
Три вектора компланарны тогда и только
тогда, когда хотя бы один из них можно
представить в виде линейной комбинации
двух других.
Доказательство.
Пусть векторы
компланарны. Возможны два случая.
1) Среди данных
векторов есть хотя бы одна пара
коллинеарных векторов. Пусть
и
коллинеарны. Тогда, по свойствам
коллинеарных векторов, хотя бы один из
них можно выразить через другой. Пусть.
Тогда,
т.е. векторесть линейная комбинация векторов
и
.
|
2) |
Рис. |
Пусть
.
По свойствам 10
и 20
следует, что вектор
компланарен с векторами
и
.
40.
Если векторы
и
не
коллинеарны, то любой компланарный с
ними вектор можно представить в виде
их линейной комбинации.
Теорема 4.
Множество
всех компланарных векторов есть двумерное
векторное пространство над
полем действительных чисел. Базисом
в нём является любая упорядоченная пара
неколлинеарных векторов.
Доказательство
следует из
предыдущих
свойств.
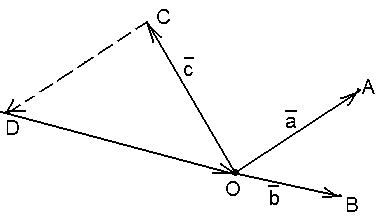
Задача 3. АВСD
и AB1C1D1
два произвольных параллелограмма.
|
Докажите, что
Решение. = |
Рис. |
Теорема 5. Если
векторы
не компланарные, то любой геометрический
вектор можно представить в виде их
линейной комбинации.
Доказательство.
Пусть векторы
не
компланарны. Очевидно, никакие два из
них не являются коллинеарными. Пусть
любой вектор. Возможны два случая.
1) Вектор
компланарен с какой-нибудь парой данных
векторов. Пусть
компланарен с векторами
и
.
Тогда по
свойству 30
компланарных векторов
.
|
2) |
Рис. |
Теорема 6.
Множество
всех геометрических векторов есть
трёхмерное
векторное пространство
над полем действительных чисел. Базисом
в нём является любая упорядоченная
тройка некомланарных векторов.
Доказательство
следует из
теоремы 5 и свойств компланарных векторов.
В курсе линейной
алгебры (в первом семестре) введены
координаты вектора в данном базисе и
рассмотрены свойства координат. Все
определения и свойства их будут
использоваться в векторных пространствах
геометрических векторов.
Если в векторном
пространстве зафиксированы два базиса
В и
В1,
Т
– матрица перехода от базиса В
к базису В1,
х и
х1
столбцы координат данного вектора
в базисахВ
и В1
соответственно, то х
= Тх1.
Если эти формулы переписать в координатах
во множестве компланарных векторов, то
получим
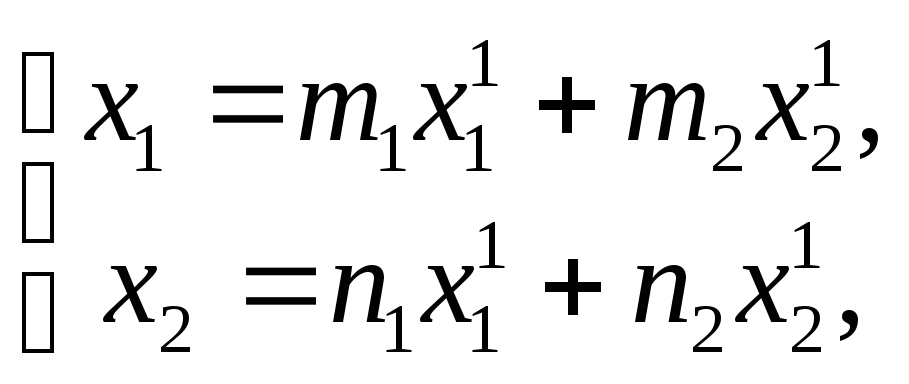
,
.
Во множестве всех
геометрических векторов
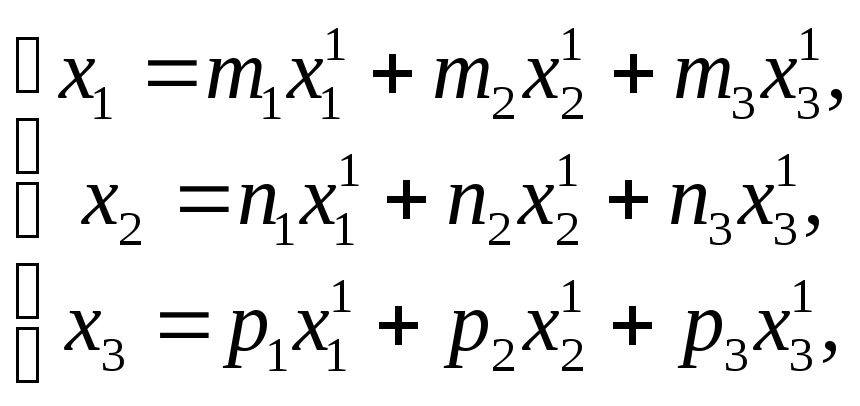
,
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейная зависимость векторов
Пусть даны три силы ,
,
, лежащие в одной плоскости. Можно ли любую из них выразить через две другие? Эта задача очень часто встречается в физике. Если
и
не лежат на одной прямой (рис. 3.15, а), то сила
может быть представлена через
, и
по правилу параллелограмма:
Рис. 3.15. Различные случаи расположения сил.
Если же и
лежат на одной прямой, то эту задачу решить не удастся (рис. 3.15, б). Решение задачи окажется невозможным и в том случае, когда сила
находится вне плоскости, которую образуют силы
,
, если они не лежат на одной прямой (рис. 3.15, в). Чтобы понять, почему это происходит, перейдем от геометрической иллюстрации этой задачи к ее строгому математическому анализу, основанному на понятии линейной зависимости векторов и исследовании свойств таких систем векторов.
Выражение вида:
Где – векторы, а
– скаляры, называется ЛИНЕЙНОЙ КОМБИНАЦИЕЙ ВЕКТОРОВ. Его смысл состоит в том, что над системой векторов производятся линейные операции, введенные выше, в результате выполнения которых получается некоторый новый вектор, возможно даже нулевой, если, например, все множители
. А если не все
равны нулю, может ли их линейная комбинация обратиться в нуль? Оказывается, что условия, определяющие эту возможность, разделяют векторы на две принципиально различные группы.
Система векторов , среди которых есть ненулевые, называется ЛИНЕЙНО ЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор при условии, что Не все скалярные множители
равны нулю, то есть
Система векторов называется ЛИНЕЙНО НЕЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор только при условии, что Все скалярные множители
равны нулю, т. е.
Очевидно, если в системе векторов есть нулевой вектор, то она линейно зависима. Для доказательства этого факта достаточно в равенстве
Взять все коэффициенты равными нулю, за исключением одного – стоящего перед нулевым вектором (он может принимать любое отличное от нуля значение). Это и будет означать линейную зависимость данной системы векторов.
Если система из n векторов включает в себя m линейно зависимых, то она линейно зависима. Действительно, пусть первые m векторов линейно зависимы. Тогда в равенстве
Хотя бы один из скалярных коэффициентов отличен от нуля. Записав формально равенство
Где не все равны нулю, получим, что система векторов
линейно зависима.
Рис. 3.16. Коллинеарные
Векторы.
Как геометрически представить себе линейно зависимые и линейно независимые векторы? Введем для этого два определения.
Векторы называются КОЛЛИНЕАРНЫМИ (рис. 3.16), если они лежат на параллельных прямых.
Нулевой вектор считается коллинеарным любому вектору.
Приведя эти векторы к общему началу, получим, что они располагаются на одной прямой.
Векторы, лежащие в параллельных плоскостях, называются КОМПЛАНАРНЫМИ (рис. 3.17). Нулевой вектор считается компланарным любой системе компланарных векторов.
Рис. 3.17. Компланарные векторы.
Если привести их к общему началу, то они окажутся расположенными в одной плоскости.
Из этих определений следует, что коллинеарность векторов можно рассматривать для системы, состоящей из двух или более векторов, а компланарность – для трех и более векторов.
Действительно, когда число векторов более одного, их приведение к одной прямой осуществимо не всегда. Для коллинеарных векторов этого удается добиться.
Термин «коллинеарность» характеризует взаимное расположение векторов, поэтому коллинеарность одного вектора лишена смысла.
Будут ли коллинеарные векторы компланарны? Будут ли компланарные векторы коллинеарны?
Аналогично, два вектора путем свободного переноса всегда можно расположить в одной плоскости. Поэтому они всегда компланарны. Этого может не быть, если число векторов больше двух. Если же векторы компланарны, то их всегда можно привести в одну плоскость.
Оказывается, коллинеарность и компланарность векторов неразрывно связаны с их линейной зависимостью. Мы докажем сейчас теоремы, которые соединяют эти понятия и служат предпосылками для введения центрального понятия всей математики – СИСТЕМЫ КООРДИНАТ.
ТЕОРЕМА 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Слова «тогда и только тогда», как известно, означают, что имеет место прямая и обратная теоремы. Сформулируем их и докажем.
Необходимость. Если два вектора линейно зависимы, то они коллинеарны.
ДОКАЗАТЕЛЬСТВО. Пусть векторы и
линейно зависимы. Тогда в равенстве
Хотя бы один из скалярных множителей или
отличен от нуля. Пусть для определенности
. Тогда
Где , что означает коллинеарность векторов
и
.
Достаточность. Если два вектора коллинеарны, то они линейно зависимы.
ДОКАЗАТЕЛЬСТВО. Пусть векторы и
коллинеарны. Тогда, очевидно, они связаны соотношением
Это означает, что линейная комбинация векторов и
обращается в нулевой вектор, причем скалярный множитель при векторе
не равен нулю, то есть система векторов
и
линейно зависима.
Наряду с доказанной теоремой, могут быть сформулированы еще две, являющиеся ее следствиями.
Сформулируйте эти утверждения с помощью предикатов.
Следствие 1. Если два вектора не являются линейно зависимыми, то они не будут коллинеарны.
Следствие 2. Если два вектора не являются коллинеарными, то они не будут линейно зависимы.
ТЕОРЕМА 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Необходимость. Если три вектора линейно зависимы, то они компланарны.
Рис. 3.18. Связь
между линейной
зависимостью
и компланарностью.
ДОКАЗАТЕЛЬСТВО. Пусть векторы ,
и
линейно зависимы (рис. 3.18). Тогда в равенстве
Хотя бы один из скалярных множителей ,
или
отличен от нуля. Пусть для определенности
. Тогда
То есть вектор – диагональ параллелограмма, построенного на векторах
и
как на сторонах (по правилу сложения векторов). Но векторы
и
, а также
И
попарно коллинеарны. Следовательно,
и
лежат в плоскости этого же параллелограмма, то есть
,
и
– компланарны.
В случае коллинеарности векторов и
компланарность
,
и
очевидна.
Достаточность. Если три вектора компланарны, то они линейно зависимы.
Рис. 3.19. Связь между компланарностью и линейной зависимостью векторов.
ДОКАЗАТЕЛЬСТВО. Пусть ,
и
компланарны (рис. 3.19), то есть они лежат в одной плоскости и хотя бы два из них, например,
и
, неколлинеарны. После приведения системы векторов к общему началу вектор
можно разложить по направлениям неколлинеарных векторов
и
, то есть представить его в виде суммы векторов, лежащих на прямых, задаваемых векторами
и
:
Но ,
, поэтому
или
.
Поскольку имеется хотя бы один скалярный множитель, отличный от нуля, то ,
и
линейно зависимы.
Могут ли быть среди трех некомпланарных векторов два коллинеарных?
Следствие 1. Если три вектора не являются линейно зависимыми, то они не будут компланарны.
Следствие 2. Если три вектора не являются компланарными, то они не будут линейно зависимы.
ТЕОРЕМА 3. Всякий вектор может быть единственным образом разложен по трем некомпланарным векторам.
Теорема означает, что если векторы ,
и
некомпланарны и вектор
произволен, то существует единственное представление
Где где L1, L2 и L3 – скаляры.
ДОКАЗАТЕЛЬСТВО. Приведем векторы ,
,
и
к общему началу (рис. 3.20). Пусть точка L – конец вектора
, а точка М – определяет пересечение вспомогательной прямой LM, параллельной вектору
, с плоскостью векторов
и
. Рассмотрим вспомогательные отрезки
. Тогда, по правилу сложения векторов,
Рис. 3.20. Разложение вектора по трем
некомпланарным
направлениям.
Но векторы и
,
и
,
и
коллинеарны, поэтому
А значит,
. (3.1)
Покажем, что это разложение единственно. Предположим противное, что существует другое представление через векторы
,
И
:
(3.2)
И хотя бы один из коэффициентов не равен соответствующему коэффициенту
. Пусть для определенности
. Тогда, вычитая из (3.1) равенство (3.2), получим:
Полученное соотношение означает, что линейная комбинация векторов ,
и
равна нулевому вектору, но скалярный коэффициент
при векторе
отличен от нуля, то есть векторы
,
и
линейно зависимы, а потому компланарны, что противоречит условию теоремы. Следовательно, предположение о справедливости равенства (3.2) наряду с равенством (3.1), неверно, то есть разложение (3.1) единственно.
Следствие. Любые четыре вектора в пространстве линейно зависимы.
Действительно, если ,
и
некомпланарны, то из равенства (3.1) следует:
Скалярный коэффициент при векторе не равен нулю. Следовательно, четыре вектора в пространстве линейно зависимы.
Если же какие-то три из векторов ,
,
,
компланарны, то они будут линейно зависимы, а значит приведут к линейной зависимости всю систему векторов.
Если какие-то два из четырех векторов коллинеарны, то это означает их линейную зависимость и, следовательно, линейную зависимость всех четырех векторов.
Таким образом, любые четыре вектора в пространстве линейно зависимы.
Вернемся теперь к задачам, поставленным в начале параграфа. Если силы и
лежат на одной прямой и силу
необходимо выразить через эти векторы, то ясно, что подобная задача неразрешима, так как всякая линейная комбинация сил
и
есть некоторый вектор
Лежащий на этой прямой и неколлинеарный вектору .
Если две из трех сил коллинеарны, то их можно параллельным переносом привести в одну плоскость, а значит они линейно зависимы. В их линейной комбинации, приравненной к нулю, есть хотя бы один коэффициент, отличный от нуля, что позволяет выразить одну силу через две другие. Если же силы ,
и
представляют собой неколлинеарные друг другу векторы, то, располагаясь в одной плоскости, они образуют линейно зависимую систему векторов, что обеспечивает возможность выразить одну из них через две другие.
Если векторы линейно зависимы, то всякий ли вектор можно выразить через остальные?
Когда одна из сил, например , лежит вне плоскости, образуемой силами
и
, то система векторов
,
,
становится некомпланарна, а значит, линейно независимой, поэтому между ними возможно лишь соотношение:
0.
| < Предыдущая | Следующая > |
|---|
В данной публикации мы рассмотрим, какие векторы называются компланарными, и перечислим условия для компланарности двух, трех и большего количества векторов. Также разберем примеры решения задач по этой теме.
- Условия компланарности векторов
- Пример задачи
Условия компланарности векторов
Векторы, лежащие в одной плоскости или параллельные ей, называются компланарными.
Из определения следует, что любые два вектора компланарны, т.к. всегда можно найти плоскость, параллельную им обоим.
Условия компланарности:
- Для трех векторов:
- Их смешанное произведение равняется нулю.
- Они линейно зависимы.
- Для n-ого количества векторов: среди них не более двух линейно независимых векторов.
Пример задачи
Определим, являются ли векторы a = {2; 5; 8}, b = {1; 4; 3} и c = {6; 7; 1} компланарными.
Решение
Чтобы проверить компланарность векторов с заданными координатами, найдем их смешанное произведение.
a · [b x c] = 8 + 90 + 56 – 192 – 42 – 5 = -85
Таким образом, векторы не являются компланарными, т.к. их смешанное произведение не равняется нулю.
Компланарные векторы
Содержание:
- Что такое компланарные векторы
-
Условия компланарности и линейная зависимость векторов
- Линейная зависимость
- Условия компланарности
- Теоремы, связанные с условием компланарности трех векторов
- Пример задачи на компланарность векторов
Что такое компланарные векторы
Определение
Векторы называются компланарными, если лежат в одной или параллельных плоскостях.
Это определение справедливо только для трех и более векторов, так как для двух направленных отрезков всегда можно найти плоскость, параллельную им.
Условия компланарности и линейная зависимость векторов
Среди условий компланарности векторов встречается понятие линейной зависимости, которое следует разобрать перед тем, как перейти непосредственно к условиям.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Линейная зависимость
Линейно зависимыми называются вектора (overline{a_1},;overline{a_2},;dots;,;overline{a_n};), которые можно составить в линейную комбинацию, равную нулю: (lambda_1cdotoverline{a_1}+;lambda_2cdotoverline{a_2}+dots+;lambda_noverline{cdot a_n};=0.)
Линейная комбинация — вектор, составленный из суммы векторов (overline{a_1},;overline{a_2},;dots;,;overline{a_n};) и коэффициентов разложения (lambda_{1,};lambda_2,;dots;,;lambda_n.)
Существует пять критериев и свойств линейной зависимости векторов:
- Хотя бы один из векторов можно представить в виде линейной комбинации других.
- В n-мерном пространстве любые n+1 векторов линейно зависимы.
- Хотя бы один из векторов — нулевой.
- Если часть системы векторов линейно зависимы, то это справедливо и для остальных.
- Если одна система векторов может быть выражена через другую и содержит больше векторов, то такая система линейно зависима.
Условия компланарности
Для неограниченного числа векторов справедливо следующее: если среди них есть не более двух линейно независимых векторов, то они компланарны.
На практике чаще всего встречаются задачи с тройками векторов. Для них существуют и другие условия компланарности:
- Если три вектора линейно зависимы, то они компланарны.
- Смешанное произведение компланарных векторов равняется нулю.
Теоремы, связанные с условием компланарности трех векторов
Правило, согласно которому три вектора компланарны, если их смешанное произведение равно нулю, проистекает из теоремы. Его также называют признаком и критерием компланарности векторов. Доказать данное утверждение можно следующим образом:
Пусть смешанное произведение ((overline atimesoverline b)cdotoverline c=0). Векторы ((overline atimesoverline b)) и (overline c) — перпендикулярны, так как их скалярное произведение равняется нулю.
В то же время, результатом векторного произведения является вектор, перпендикулярный перемножаемым. Таким образом, векторы overline a,overline b,overline c перпендикулярны одному и тому же вектору (overline atimesoverline b), то есть лежат в параллельных плоскостях. Значит, векторы компланарны.
Для проверки, к доказательству данной теоремы можно подойти с другой стороны:
Пусть векторы overline a,overline b,overline c компланарны.
Необходимо доказать, что их смешанное произведение ((overline atimesoverline b)cdotoverline c) равняется нулю. Так как данные вектора компланарны, то ((overline atimesoverline b)) перпендикулярен каждому из них.
Отсюда следует, что его скалярное произведение с вектором overline c будет равняться нулю. Это, в свою очередь, означает, что смешанное произведение ((overline atimesoverline b)cdotoverline c=0.)
Пример задачи на компланарность векторов
Задача
Даны точки A(1, 2, -1), B(0, -1, 5), C(-1, 2, 1) и D(2, 1, 3). Проверить, принадлежат ли они одной плоскости.
Решение
Сперва необходимо построить на основе имеющихся точек векторы (overline{AB},;overline{AC},;overline{AD}:)
(overline{AB}=(0-1,;(-1)-2,;5-(-1))=(-1,;3,;6))
(overline{AС}=((-1)-1,;2-2,;1-(-1))=(-2,;0,;2))
(overline{AВ}=(2-1,;1-2,;3-(-1))=(1,;-1,;4))
Чтобы проверить, принадлежать ли точки одной плоскости, необходимо найти смешанное произведение полученных векторов. Если оно равняется нулю, то векторы компланарны, следовательно, точки лежат в одной плоскости. В противном случае ответ на поставленный в условии вопрос будет отрицательным.
Смешанное произведение рассчитывается по формуле нахождения определителя матрицы:
((overline{AВ}timesoverline{AC})cdotoverline{AD}=begin{vmatrix}-1&-3&6\-2&0&2\1&-1&4end{vmatrix}=((-1)cdot0cdot4)+((-3)cdot2cdot1)+((-2)cdot(-1)cdot6)-(6cdot0cdot1)-((-1)cdot2cdot(-1))-((-3)cdot(-2)cdot4)=0-6+12-0-2-24=-20)
Полученное число не равно нулю, следовательно, векторы некомпланарны. Это значит, что точки не лежат в одной плоскости.
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 1).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
-
Для 3-х векторов. Три вектора компланарны если они линейно зависимы.
-
Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
Примеры задач на компланарность векторов
Пример 1. Проверить компланарны ли три вектора a = {1; 2; 3},
b = {1; 1; 1}, c = {1; 2; 1}.
Решение: найдем смешанное произведение векторов
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Пример 2. Доказать что три вектора a = {1; 1; 1},
b = {1; 3; 1} и c = {2; 2; 2} компланарны.
Решение: найдем смешанное произведение векторов
| a · [b × с] = | 1 | 1 | 1 | = |
| 1 | 3 | 1 | ||
| 2 | 2 | 2 |
= 1·2·3 + 1·1·2 + 1·1·2 — 1·2·3 — 1·1·2 — 1·1·2 = 6 + 2 + 2 — 6 — 2 — 2 = 0
Ответ: вектора компланарны так, как их смешанное произведение равно нулю.
Пример 3. Проверить коллинеарны ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1}, d = {3; 3; 3}.
Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования
| 1 | 1 | 1 | ~ | ||
| 1 | 2 | 0 | |||
| 0 | -1 | 1 | |||
| 3 | 3 | 3 |
из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ~ | ||||
| 1 — 1 | 2 — 1 | 0 — 1 | 0 | 1 | -1 | |||||||
| 0 | -1 | 1 | 0 | -1 | 1 | |||||||
| 3 — 3 | 3 — 3 | 3 — 3 | 0 | 0 | 0 |
к 3-тей строке добавим 2-рую
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ||||
| 0 | 1 | -1 | 0 | 1 | -1 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 | 0 | 0 | ||||||
| 3 — 3 | 3 — 3 | 3 — 3 | 0 | 0 | 0 |
Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.
Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.