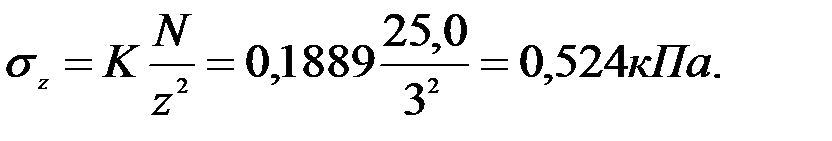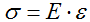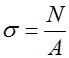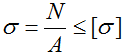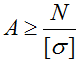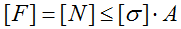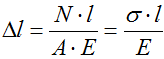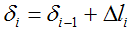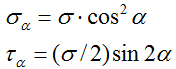Определение сжимающих напряжений от внешнего воздействия
Контрольная работа
по дисциплине: механика грунтов
Цель при изучении дисциплины «Механика грунтов» заключается в формировании у студентов знаний и умений в области строительства и эксплуатации транспортных сооружений. В задачи дисциплины входят:
ü изучение принципов и методов расчета напряженно – деформированного состояния грунтового массива;
ü оценка его прочности и устойчивости.
В результате изучения дисциплины студент должен уметь:
ü формулировать и решать задачи связанные с прогнозом полных осадок транспортных сооружений;
ü владеть методами оценки устойчивости склонов, откосов и массивных подпорных стенок.
Механические свойства грунтов
При анализе механических свойств грунтов испытания проводят на образцах грунта, тщательно отобранных в полевых условиях стараясь сохранить их природную структуру. Уплотнения грунта под действием внешнего давления рассматривают по трем основным схемам:
1. сжатие без ограничения возможности бокового расширения (штамповые испытания);
2. сжатие без возможности бокового расширения (компрессионные испытания в одометрах);
3. трехосное сжатие при ограниченной возможности бокового расширения (испытания в приборе трехосного сжатия – стабилометре).
При изысканиях мостового перехода, для расчета осадки насыпи, по данным отбора проб геологической колонки в лабораторию был доставлен суглинок аллювиальный характеризующийся следующими парпметрами:
| Наименование показателей | Суглинок аллювиальный |
| Удельный вес (плотность) γ, г/см | 2,72 |
| Объемная масса γ ,г/см | 2,01 |
| Влажность грунта W ,% | |
| Полная осадка ∆h по индикатору, мм При степени нагрузки, МПа | |
| 0,00 | |
| 0,1 | 0,11 |
| 0,2 | 0,14 |
| 0,3 | 0,17 |
| 0,4 | 0,19 |
| 0,5 | 0,21 |
| 0,6 | 0,23 |
| 0,7 | 0,24 |
Необходимо построить компрессионную кривую ек = f (Р), определить коэффициент сжимаемости (уплотнения) mо в диапазоне от 0,1 до 0,2 МПа и модуль общей деформации Ео если начальная высота образца hо = 30 мм.
Образец суглинка аллювиального имеет следующие параметры: удельный вес (плотность) γ = 2,72 г/см 3 ; начальная влажность Wо = 24 %; объемная масса γоб = 2,01 г/см 3 ; высота образца hо = 30 мм. Образец был помещен в компрессионный прибор одноосного сжатия – одометр ПЛЛ-9. По данным компрессионных испытаний были получены следующие значения полной осадки по индикатору ∆h (табл.2, столбец 2) для каждой ступени нагрузки.
Коэффициент пористости e это отношение объема пор к объему частиц исследуемого образца. Различают начальный коэффициент пористости (до сжатия, в естественном состоянии) – eои конечный eк после приложения нагрузки. При сжатии без возможности бокового расширения грунта можно воспользоваться зависимостью
где ε0 — относительная осадка.
| Ступень нагрузки Р, МПа | Полная осадка по индикатору ∆h, мм | Относительная осадка ε = ∆h / h | Коэффициент пористости е |
| 0,00 | 0,0000 | 0,678 | |
| 0,1 | 0,11 | 0,0040 | 0,671 |
| 0,2 | 0,14 | 0,0053 | 0,669 |
| 0,3 | 0,17 | 0,0063 | 0,667 |
| 0,4 | 0,19 | 0,0070 | 0,666 |
| 0,5 | 0,21 | 0,0077 | 0,665 |
| 0,6 | 0,23 | 0,0080 | 0,664 |
| 0,7 | 0,24 | 0,0083 | 0,664 |
Начальный коэффициент пористости определится как:

где γск – объемная масса скелета грунта, г/см 3 ,

По данным таблицы 2 строим компрессионную кривую eк=f(P), изображенную на рис. 2.
Рис.1. Компрессионная кривая
В результате отсыпки насыпи нагрузка на основание увеличилась с Р1=0 МПа до Р2=0,1 МПа. Следовательно для этого диапазона давлений коэффициент уплотнения определится как:

Если коэффициент уплотнения находится в диапазоне:
m0‹ 0,0005 – то грунт малосжимаемый,
при 0,0005 ‹ m0 ‹ 0,005 – грунт среднесжимаемый,
при m0 › 0,005 – грунт сильносжимаемый.
В нашем случае грунт сильносжимаемый.
Модуль общей деформации определится по зависимости

Но это компрессионный модуль и он несколько отличается от реального полученного в естественных условиях.
Определение сжимающих напряжений от внешнего воздействия
Для расчета грунтовых оснований необходимо знать, как распределяются напряжения в массиве грунта. В механике грунтов такую задачу можно решить для линейно-деформируемого однородного изотропного полупространства, ограниченного сверху горизонтальной плоскостью, к которой приложена внешняя нагрузка. Для сосредоточенной силы напряжение в любой точке М полупространства (рис.2) определится как

где σz – сжимающее напряжение, МПа; k – коэффициент, который учитывает положение рассматриваемой точки,

Р – сосредоточенная сила; z – глубина рассматриваемой точки; r – расстояние от оси приложения сосредоточенной силы.
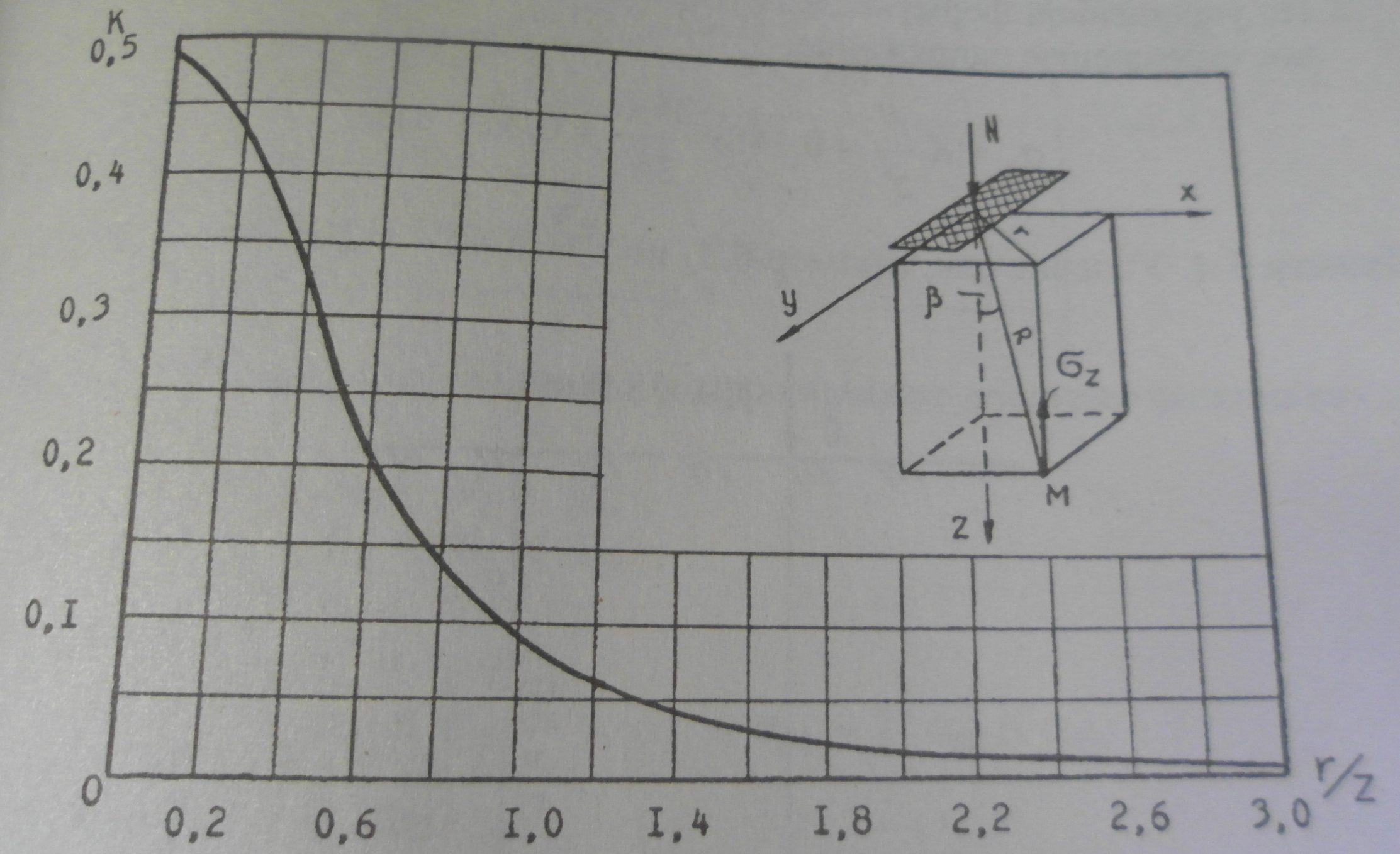
Рис.2. Схема действия на точку М сосредоточенной силы Р: ß – угол видимости; σR – результирующее напряжение, которое раскладывается на σz, σzx, σzy; z – глубина
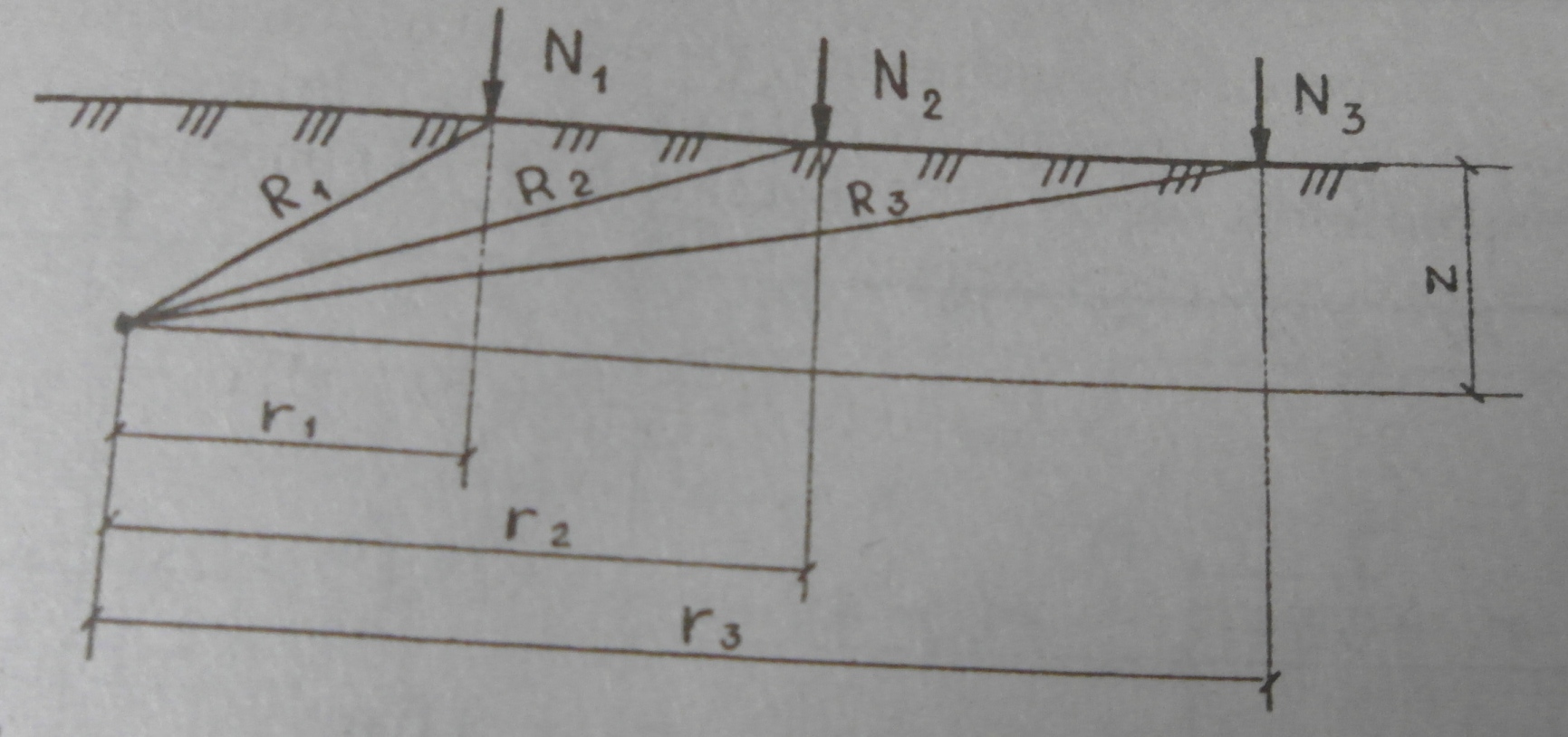
При действии нескольких сосредоточенных сил сжимающее напряжение определяется суммированием
Найти вертикальное сжимающее напряжение (σz) для точки Арасположенной согласно своего варианта. Построить эпюру сжимающих напряжений на глубине расположения точки и эпюру по оси действия сосредоточенной силы.
| Величина сосредоточенной силы Р, МН | 0,7 |
| Глубина расположения точки z, м | 3,0 |
| Расстояние от линии действия силы r, м | 2,4 |
Найдем вертикальное сжимающее напряжение (σz) для точки А, расположенной на глубине 3,0 м и в стороне на 2,4 м от линии действия силы Р = 0,7 МН.
2.1. Для точки А имеем: z = 3,0 м; r = 2,4 м; соотношение r / z = 0,8.
По приложению 1 или по формуле 2 определяем k = 0,. По формуле 1
2.2.Задавясь значением r через 0,25м построим эпюру сжимающих напряжений на глубине z = 3.0 м. Значения сводим в табл.3.
| r, м | 0,00 | 0,25 | 0,50 | 0,75 | 1,00 | 1,25 |
| δ , МПа | 0,037 | 0,036 | 0,033 | 0,029 | 0,025 | 0,020 |
| r, м | 1,50 | 1,75 | 2,00 | 2,25 | 2,50 | 2,75 |
| δ , МПа | 0,016 | 0,012 | 0,010 | 0,008 | 0,006 | 0,005 |
2.3. Задавясь значением z через 0,25 м построим эпюру сжимающих напряжений по глубине вдоль оси действия внешней силы. Значения сводим в табл.4.
Источник
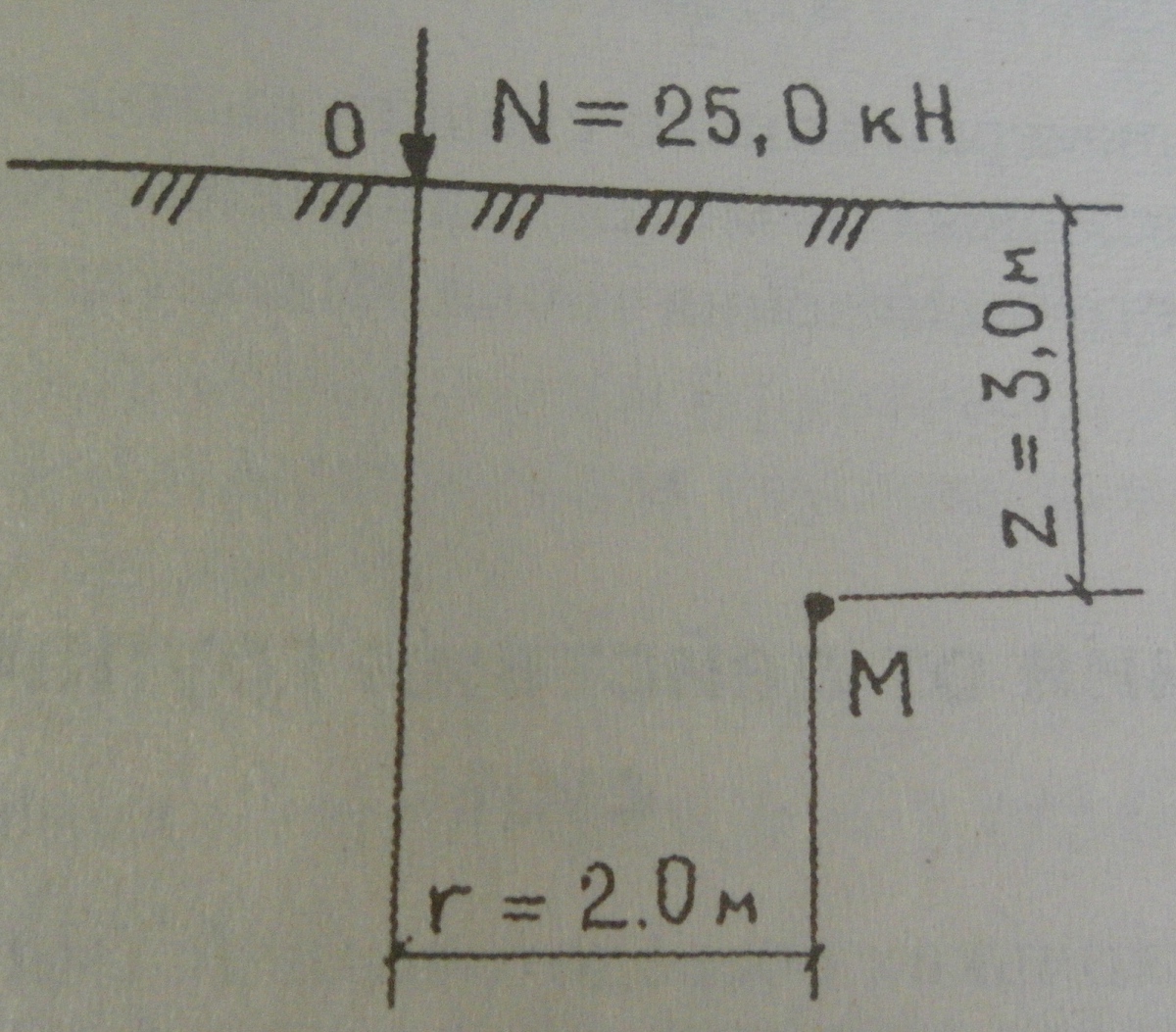
Пример 1. Определить вертикальное сжимающее напряжение в точке М от действия сосредоточенной силы N, приложенной к поверхности грунтового основания
Определить вертикальное сжимающее напряжение в точке М от действия сосредоточенной силы N, приложенной к поверхности грунтового основания, если известно: N=25.0кН, точка М находится на глубине 3 м от поверхности и на расстоянии 2 м в сторону от действия силы.
График для определения коэффициента К.
Решение: 1. Определяем отношение r/z=2/3=0,67. По графику находим соответствует К=0,1889.
2. По упрощенной формуле Ж. Буссинеска определяем вертикальное сжимающее напряжение:
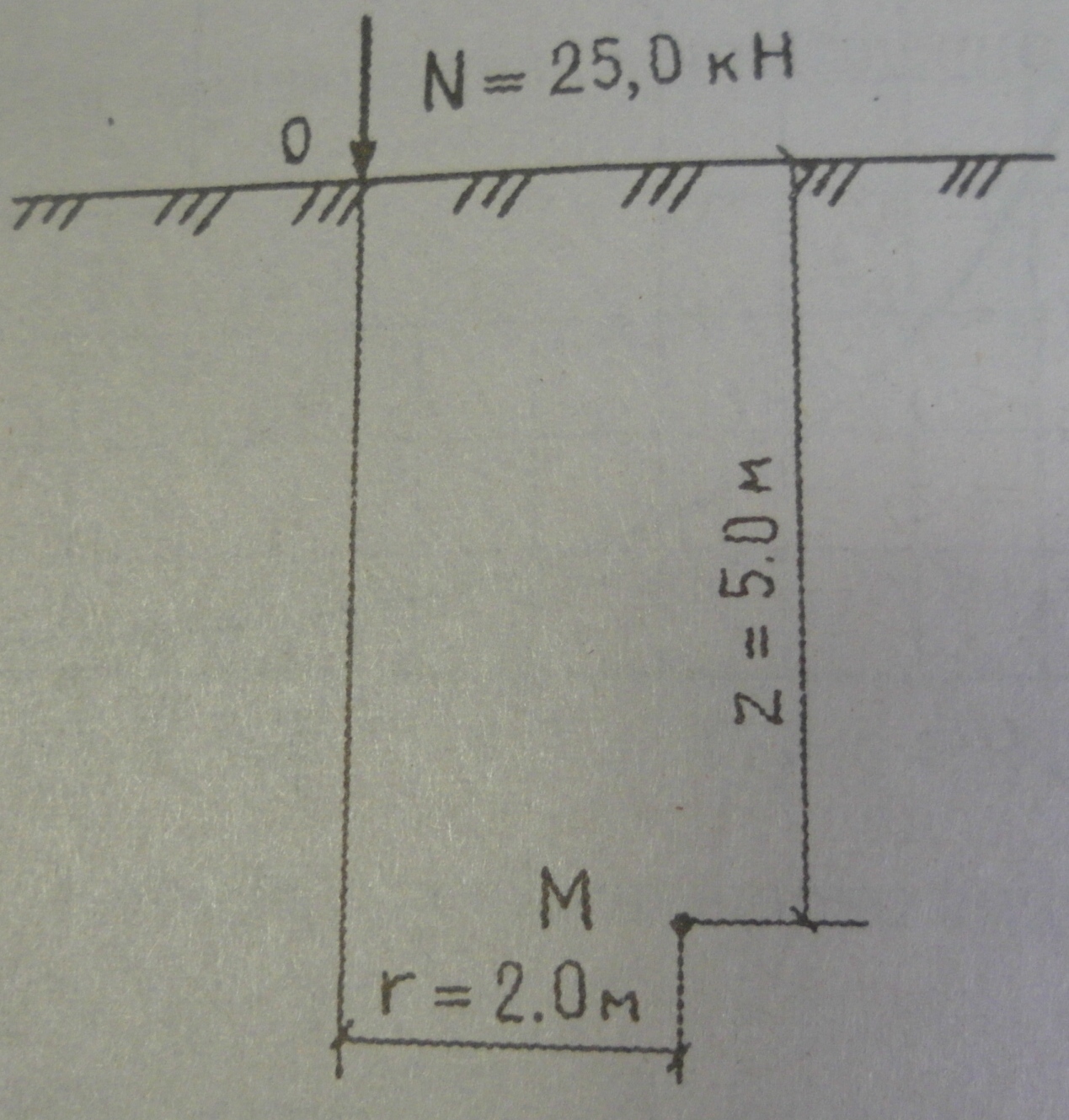
Пример 2. Условие (см. пример 1) по z=5 м; r=2 м.
Решение: 1. r/z=2/5=0.4, следовательно, по графику К=0,3294.
2. 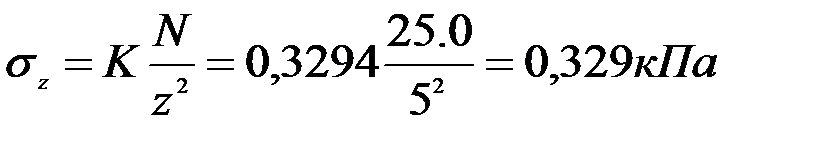
Вывод: вертикальное сжимающее напряжение зависит от места положения точки, например, с увеличением глубины (место положения точки М) и с удалением от оси напряжения уменьшается.
Напряжения от действия нескольких сосредоточенных сил.
Схема к определению напряжений от действия нескольких сил.
В основе – принцип суперпозиций. Суммарное напряжение равно сумме напряжения от каждой силы.
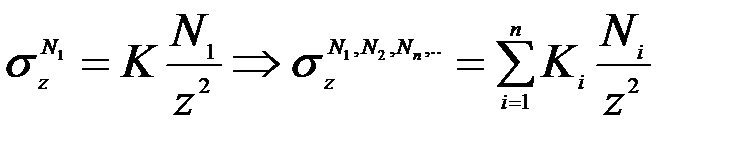
Дата добавления: 2015-08-08 ; просмотров: 2142 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Определение сжимающих напряжений по методу угловых точек.
Знание величины сжимающих напряжений для угловых точек под прямоугольной площадью загрузки позволяет очень быстро вычислять сжимающие напряжения для любой точки полупространства, особенно если пользоваться значениями угловых коэффициентов Кс (табл.9).
Для площадок под центром загруженного прямоугольника сжимающее напряжение ах0 будет равно
Значения коэффициентов / и /’ [формулы (111.9) и (111.10)]
| Прямоугольные фундаменты с отношением сторон а=,//* | ||||||||||||
| р | п га | 1,2 | 1,6 | 1,8 | 2,4 | 2,8 | 3,2 | |||||
| 0,0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,4 | 0,949 | 0,960 | 0,968 | 0,972 | 0,974 | 0,975 | 0,976 | 0,976 | 0,977 | 0,977 | 0,977 | 0,977 |
| 0,8 | 0,756 | 0,800 | 0,830 | 0,848 | 0,859 | 0,866 | 0,870 | 0,875 | ‘ 0,878 | 0,879 | 0,880 | 0,881 |
| 1,2 | 0,547 | 0,606 | 0,652 | 0,682 | 0,703 | 0,717 | 0,727 | 0,740 | 0,746 | 0,749 | 0,753 | 0,754 |
| 1,6 | 0,390 | 0,449 | 0,496 | 0,532 | 0,558 | 0,578 | 0,593 | 0,612 | 0,623 | 0,630 | 0,639 | 0,639 |
| 2,0 | 0,285 | 0,336 | 0,379 | 0,414 | 0,441 | 0,463 | 0,481 | 0,505 | 0,520 | 0,529 | 0,540 | 0,545 |
| 2,4 | 0,214 | 0,257 | 0,294 | 0,325 | 0,352 | 0,374 | 0,392 | 0,419 | 0,437 | 0,449 | 0,462 | 0,470 |
| 2,8 | 0,165 | 0,201 | 0,232 | 0,260 | 0,284 | 0,304 | 0,321 | 0,350 | 0,369 | 0,383 | 0,400 | 0,410 |
| 3,2 | 0,130 | 0,160 | 0,187 | 0,210 | 0,232 | 0,251 | 0,267 | 0,294 | 0,314 | 0,329 | 0,348 | 0,360 |
| 3,6 | 0,106 | 0,130 | 0,153 | 0,173 | 0,192 | 0,209 | 0,224 | 0,250 ■ | 0,270 | 0,285 | 0,305 | 0,320 |
| 4,0 | 0,087 | 0,108 | 0,127 | 0,145 | 0,161 | 0,176 | 0,190 | 0,214 | 0,233 | 0,248 | 0,270 | 0,285 |
| 4,4 | 0,073 | 0,091 | 0,107 | 0,122 | 0,137 | 0,150 | 0,163 | 0,185 | 0,203 | 0,218 | 0,239 | 0,256 |
| 4,8 | 0,062 | 0,077 | 0,092 | 0,105 | 0,118 | 0,130 | 0,141 | 0,161 | 0,178 | 0,192 | 0,213 | 0,230 |
| 5,2 | 0,053 | 0,066 | 0,079 | 0,091 | 0,102 | 0,112 | 0,123 | 0,141 | 0,157 | 0,170 | 0,191 | 0,208 |
| 5,6 | 0,046 | 0,058 | 0,069 | 0,079 | 0,089 | 0,099 | 0,108 | 0,124 | 0,139 | 0,152 | 0,172 | 0,189 |
| 6,0 | 0,040 | 0,051 | 0,060 | 0,070 | 0,078 | 0,087 | 0,095 | 0,110 | 0,124 | 0,136 | 0,155 | 0,172 |
| 6,4 | 0,036 | 0,045 | 0,053 | 0,062 | 0,070 | 0,077 | 0,085 | 0,098 | 0,111 | 0,122 | 0,141 | 0,158 |
| 6,8 | 0,032 | 0,040 | 0,048 | 0,055 | 0,062 | 0,069 | 0,076 | 0,088 | 0,100 | 0,110 | 0,128 | 0,144 |
| 7,2 | 0,028 | 0,036 | 0,042 | 0,049 | 0,056 | 0,062 | 0,068 | 0,080 | 0,090 | 0,100 | 0,117 | 0,133 |
| 7,6 | 0,024 | 0,032 | 0,038 | 0,044 | 0,050 | 0,056 | 0,062 | 0,072 | 0,082 | 0,091 | 0,107 | 0,123 |
| 8,0 | 0,022 | 0,029 | 0,035 | 0,040 | 0,046 | 0,051 | 0,056 | 0,066 | 0,075 | 0,084 | 0,098 | 0,113 |
| 8,4 | 0,021 | 0,026 | 0,032 | 0,037 | 0,042 | 0,046 | 0,051 | 0,060 | 0,069 | 0,077 | 0,091 | 0,105 |
| 8,8 | 0,019 | 0,024 | 0,029 | 0,034 | 0,038 | 0,042 | 0,047 | 0,055 | 0,063 | 0,070 | 0,084 | 0,098 |
| 9,2 | 0,018 | 0,022 | 0,026 | 0,031 | 0,035 | 0,039 | 0,043 | 0,051 | 0,058 | 0,065 | 0,078 | 0,091 |
| 9,6 | 0,016 | 0,020 | 0,024 | 0,028 | 0,032 | 0,036 | 0,040 | 0,047 | 0,054 | 0,060 | 0,072 | 0,085 |
| 0,015 | 0,019 | 0,022 | 0,026 | 0,030 | о.озз | 0,037 | 0,044 | 0,050 | 0,056 | 0,067 | 0,079 | |
| 0,011 | 0,017 | 0,020 | 0,023 | 0,027 | 0,029 | 0,033 | 0,040 | 0,044 | 0,050 | 0,060 | 0,071 | |
| 0,009 | 0,015 | 0,018 | 0,020 | 0,024 | 0,026 | 0,028 | 0,034 | 0,038 | 0,044 | 0,051 | 0,060 |
1,000 0,977 0,881 0,755 0,642 0,550 0,477 0,420 0,374 0,337 0,306 0,280 0,258 0,239 0,223 0,208 0,196 0,184 0,175 0,166 0,158 0,150 0,144 0,137 0,132 0,126 0,114 0,104
Примечание. Для промежуточных значений а и величины коэффициентов определяются интерполяцией.
и для площадок под углом загруженного прямоугольника
где Д’о и Д’с — табличные коэффициенты;
р— интенсивность равномерно распределенной нагрузки.
Значения коэффициентов Ко и Кс определяются по табл. 9 как функции относительной глубины $=2г/Ь или $=г/Ь (по СНиПу — т) и соотношения сторон прямоугольной площади загрузки (а = = Щ (по СНиПу — п):
Последние выражения позволяют пользоваться одной таблицей как при вычислении коэффициентов для центральных точек Ко, так и для угловых Кс-
Рис. 44. Схема разбивки прямоугольной площади загрузки при
определении напряжений по методу угловых точек
Максимальное сжимающее напряжение макс аг будет в точках, расположенных под центром загруженной площади, и вычисляется по формуле (Ш.7).
Метод угловых точек для определения величины сжимающих напряжений ах применяется тогда, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась бы угловой. Тогда сжимающее напряжение в этой точке (для горизонтальных площадок, параллельных плоской границе полупространства) будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.
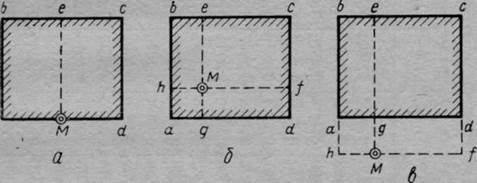
Поясним сказанное, рассмотрев три основных случая:
1) точка М находится на контуре прямоугольника внешних давлений (рис. 44, а);
2) точка М — внутри прямоугольника давлений (рис. 44, б);
3) точка М — вне прямоугольника давлений (рис. 44, в).
Значения вс /(1 + д0) в точках на разных глубинах, расположенных на угловых вертикалях при равномерно распределенной
по прямоугольной площади нагрузке р в долях от р
0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 3,0 4,0 6,0 8,0 10,0 0,0 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,2 0,2439 0,3405 0,3804 0,4003 0,4114 0,4183 0,4230 0,4259 0,4281 0,4297 0,4337 0,4352 0,4363 0,4367 0,4369 0,4 0,1363 0,2280 0,2810 0,3119 0,3308 0,3430 0,3515 0,3570 0,3612 0,3643 0,3721 0,3750 0,3771 0,3779 0,3782 0,6 0,0874 0,1578 0,2074 0,2406 0,2630 0,2782 0,2890 0,2967 0,3024 0,3068 0,3179 0,3222 0,3454 0,3265 0,3270 0,8 0,0607 0,1136 0,1552 0,1812 0,2087 0,2251 0,2371 0,2458 0,2529 0,2582 0,2721 0,2776 0,2818 0,2833 0,2840 1,0 0,0443 0,0846 0,1185 0,1456 0,1667 0,1828 0,1952 0,2047 0,2121 0,2180 0,2341 0,2406 0,2457 0,2476 0,2486 1,2 0,0336 0,0649 0,0924 0,1156 0,1344 0,1495 0,1616 0,1711 0,1788 0,1850 0,2026 0,2101 6,2162 0,2182 0,2193 1,4 0,0262 0,0510 0,0735 0,0931 0,1097 0,1235 0,1348 0,1441 0,1518 0,1580 0,1766 0,1848 0,1915 0,1940 0,1952 1,6 0,0209 0,0410 0,0596 0,0762 0,0906 0,1030 0,1135 0,1223 0,1296 0,1358 0,1549 0,1638 0,1711 0,1739 0,1753 1,8 0,0171 0,0336 0,0491 0,0632 0,0758 0,0868 0,0964 0,1046 0,1116 0,1177 0,1368 0,1460 0,1540 0,1571 0,1588 2,0 0,0142 0,0280 0,0410 0,0531 0,0641 0,0739 0,0826 0,0900 0,0967 0,1024 0,1214 0,1310 0,1395 0,1428 0,1445 2,5 0,0094 0,0187 0,0276 0,0361 0,0440 0,0514 0,0581 0,0642 0,0696 0,0745 0,0921 0,1020 0,1114 0,1153 0,1173 3,0 0,0067 0,0133 0,0198 0,0260 0,0319 0,0375 0,0427 0,0475 0,0520 0,0561 0,0718 0,0814 0,0913 0,0957 0,0980 5,0 0,0025 0,0050 0,0074 0,0099 0,0122 0,0146 0,0168 0,0190 0,0212 0,0232 0,0322 0,0391 0,0481 0,0532 0,0561 7,0 0,0013 0,0026 0,0038 0,0051 0,0064 0,0076 0,0088 0,0100 0,0111 0,0124 0,0177 0,0224 0,0293 0,0339 0,0370 10,0 0,0006 0,0013 0,0019 0,0025 0,0032 0,0038 0,0044 0,0047 0,0056 0,0067 0,0091 0,0118 0,0163 0,0198 0,0224
Примечания: Ь — ширина загруженного прямоугольника в плоскости чертежа; / — длина в направлении, перпендикулярном плоскости чертежа.
В первом случае величина а2 определится как сумма двух угловых напряжений, соответствующих прямоугольникам загрузки МаЬе и Меси, т. е.
где Л’1с и /»2с— угловые коэффициенты, определяемые по формуле (111.10) и данным табл. 9 в зависимости от относительной глубины р = г/й и отношения сторон сх ==ЦЪ;
р — интенсивность внешней равномерно распределенной нагрузки.
Во втором случае необходимо суммировать угловые напряжения от четырех прямоугольных площадей загрузки: МдаН, МНЬе, Мес и МЛц. т. е.
В третьем случае напряжение в точке М складывается из суммы напряжений от действия нагрузки по прямоугольникам МНЬе и Мес, взятых со знаком «плюс», и напряжений от действия нагрузки по прямоугольникам МИа@ и М§с1<, взятых со знаком «минус», т. е.
где /Сю, /Сгс, /Сзс, /Сю — угловые коэффициенты, определяемые по формуле (111.10) и табл. 9 в зависимости от соответствующих величин а = 11Ь и $ = г/Ь.
Для облегчения расчетов в табл. 11 приведены заранее вычисленные более подробные значения угловых коэффициентов Кс’ = = <«‘(г1Ь, 1/Ь), позволяющие обходиться без формулы (111.10), используя лишь выражение (П1.8), т. е.
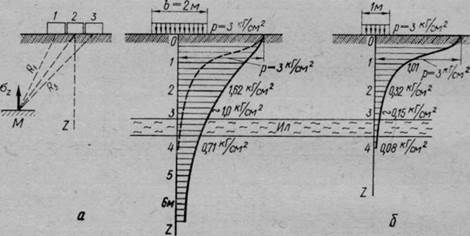
Пример 2. Определить величину сжимающих напряжений под центром и под серединой длинной стороны загруженного прямоугольника размером 2×8 м на глубине 2 м от поверхности при внешней нагрузке интенсивностью р = 3 кГ/см2,
Для площадки под центром загруженной площади
По табл. 9 коэффициент Ко = 0,54; тогда
аг0 = К0р = 0,54-3 = 1,62 кГ1см*.
Для. площадки под серединой длинной стороны прямоугольной площадки загрузки, разделяя ее на два прямоугольника размером 4×2 м, так чтобы рассматриваемая точка была бы угловой, 2 = 2 м; р = г/Ь=1;
Интеополируя по табл. 9, по формуле (ШЛО) получим
0,2500 0,2486 0,2401 0,2229 0,1999 0,1752 0,1516 0,1308 0,1123 0,0969 0,0840 0,0732 0,0642 0,0566 0,0502 0,0447 0,0401 0,0361 0,0326 0,0296 0,0270 0,0247 0,0227 0,0209 0,0193 0,0179 0,0127 0,0094 0,0073 0,0058 0.0047
0,2500 0,2489 0,2420 0,2275 0,2075 0,1851 0,1626 0,1423 0,1241 0,1083 0,0947 0,0832 0,0734 0,0651 0,0580 0,0519 0,0467 0,0421 0,0382 0,0348 0,0318 0,0291 0,0268 0,0247 0,0229 0,0212 0,0151 0,0112 0,0087 0,0069 0,0056
0,2500 0,2490 О,2429 0,2300 0,2120 0,1911 0,1705 О,1508 0,1329 0,1172 0,1034 0,0917 0,0813 0,0725 0,0649 0,0583 0,0526 0,0477 0,0433 0,0395 0,0362 0,0333 0,0306 0,0283 0,0262 0,0243 0,0174 0,0130 0,0101 0,0080 0.0065
0,2500 0,2491 0,2434 0,2315 0,2147 0,1955 О,1758 О,1569 0,1396 0,1241 0,1103 0,0984 0,0879 0,0788 0,0709 0,0640 0,0580 0,0527 0,0480 0,0439 0,0403 0,0371 0,0343 0,0317 0,0294 0,0274 0,0196 0,0147 0,0114 0,0091 0,0074
О,2500 0,2491 0,2437 0,2324 0,2165 0,1981 0,1793 0,1613 0,1445 О,1294 0,1158 0,1039 0,0934 0,0842 0,0761 0,0690 0,0627 0,0571 0,0523 0,0479 0,0441 0,0407 0,0376 0,0348 0,0324 0,0302 0,0218 0,0161 0,0127 0,0102 0,0083
0,2500 0,2491 0,2439 0,2329 0,2176 0,1999 0,1818 0,1644 0,1482 0,1334 0,1202 0,1084 0,0979 0,0887 0,0805 0,0732 0,0668 0,0611 0,0561 0,0516 0,0474 0,0439 0,0407 О,0378 0,0352 О,0328 0,0238 0,0180 0,0140 0,0112 0,0092
0,2500 0,2492 0,2440 0,2333 0,2183 0,2012 0,1836 0,1667 0,1509 0,1365 0,1236 0,1120 0,1016 0,0924 0,0842 0,0769 0,0704 0,0646 0,0594 0,0548 0,0507 0,0469 0,0436 0,0405 0,0378 0,0353 0,0257 0,0195 0,0153 0,0122 0,0100
),2500 ),2492 1,2441 ),2335 ),2188 1,2020 1,1849 1,1685 1,1530 1,1389 ),1263 ),1149 ),1047 1,0955 ),0875 ),0801 ),0735 1,0677 ),0624 ),0577 1,0535 1,0496 1,0462 ),0430 1,0402 1,0376 1,0276 1,0210 1,0165 1,0132 1,0109
0,2500 0,2492 0,2442 0,2337 0,2192 0,2026 0,1858 0,1696 0,1545 0,1408 0,1284 0,1172 0,1071 0,0981 0,0900 0,0828 0,0762 0,0704 0,0651 0,0603 0,0560 0,0521 0,0485 0,0453 0,0424 0,0397 0,0293 0,0224 0,0176 0,0142 0,0117
0,2500 0,2492 0,2442 0,2338 0,2194 0,2031 0,1865 0,1705 0,1557 0,1423 0,1300 0,1191 0,1092 0,1003 0,0923 0,0851 0,0786 0,0727 0,0674 0,0626 0,0588 0,0543 0,0507 0,0474 0,0444 0,0417 0,0310 0,0238 0,0187 0,0152 0,0125
0,2500 0,2492 0,2442 0,2339 0,2196 0,2034 0,1870 0,1712 0,1567 0,1434 0,1314 0,1205 0,1108 0,1020 0,0942 0,0870 0,0806 0,0747 0,0694 0,0646 0,0603 0,0563 0,0527 0,0493 0,0463 0,0435 0,0325 0,0251 0,0198 0,0161 0,0132
| Значения | а- ЦЬ | ||||||||
| 9— | |||||||||
| ь | 3,2 | 3,4 | 3,6 , | 3,8 | |||||
| 0,0 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 |
| 0,2 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 |
| 0,4 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 |
| 0,6 | 0,2340 | 0,2340 | 0,2341 | 0,2341 | 0,2341 | 0,2342 | 0,2342 | 0,2342 | 0,2342 |
| 0,8 | 0,2198 | 0,2199 | 0,2199 | 0,2200 | 0,2200 | 0,2202 | 0,2202 | 0,2202 | 0,2202 |
| 1,0 | 0,2037 | 0,2039 | 0,2040 | 0,2041 | 0,2042 | 0,2044 | 0,2045 | 0,2046 | 0,2046 |
| 1,2 | 0,1873 | 0,1876 | 0,1878 | 0,1880 | 0,1882 | 0,1885 | 0,1888 | 0,1888 | 0,1888 |
| 1,4 | 0,1718 | 0,1722 | 0,1725 | 0,1728 | 0,1730 | 0,1735 | 0,1739 | 0,1739 | 0,1740 |
| 1,6 | 0,1574 | 0,1580 | 0,1584 | 0,1587 | 0,1590 | 0,1598 | 0,1602 | 0,1604 | 0,1604 |
| 1,8 | 0,1443 | 0,1450 | 0,1455 | 0,1460 | 0,1463 | 0,1474 | 0,1480 | 0,1482 | 0,1482 |
| 2,0 | 0,1324 | 0,1332 | 0,1339 | 0,1345 | 0,1350 | 0,1363 | 0,1371 | 0,1373 | 0,1374 |
| 2,2 | 0,1218 | 0,1227 | 0,1235 | 0,1242 | 0,1248 | 0,1264 | 0,1274 | 0,1277 | 0,1277 |
| 2,4 2,6 | 0,1122 | 0,1133 | 0,1142 | 0,1150 | 0,1156 | 0,1175 | 0,1188 | 0,1191 | 0,1192 |
| 0,1035 | 0,1047 | 0,1058 | 0,1066 | 0,1073 | 0,1095 | 0,1111 | 0,1115 | 0,1116 | |
| 2,8 | 0,0957 | 0,0970 | 0,0982 | 0,0991 | 0,0999 | 0,1024 | 0,1041 | 0,1047 | 0,1048 |
| 3,0 | 0,0887 | 0,0901 | 0,0913 | 0,0923 | 0,0931 | 0,0959 | 0,0980 | 0,0986 | 0,0987 |
| 3,2 | 0,0823 | 0,0838 | 0,0850 | 0,0861 | 0,0870 | 0,0900 | 0,0923 | 0,0930 | 0,0933 |
| 3,4 | 0,0765 | 0,0780 | 0,0793 | 0,0804 | 0,0814 | 0,0847 | 0,0873 | 0,0880 | 0,0882 |
| 3,6 | 0,0712 | 0,0728 | 0,0741 | 0,0753 | 0,0763 | 0,0799 | 0,0826 | 0,0835 | 0,0837 |
| 3,8 | 0,0664 | 0,0680 | 0,0694 | 0,0706 | 0,0717 | 0,0753 | 0,0784 | 0,0794 | 0,0796 |
| 4,0 | 0,0620 | 0,0636 | 0,0650 | 0,0663 | 0,0674 | 0,0712 | 0,0745 | 0,0756 | 0,0758 |
| 4,2 | 0,0581 | 0,0596 | 0,0610 | 0,0623 | 0,0634 | 0,0674 | 0,0709 | 0,0721 | 0,0724 |
| 4,4 | 0,0544 | 0,0560 | 0,0574 | 0,0586 | 0,0597 | 0,0639 | 0,0676 | 0,0689 | 0,0692 |
| 4,6 | 0,0510 | 0,0526 | 0,0540 | 0,0553 | 0,0564 | 0,0606 | 0,0644 | 0,0659 | 0,0663 |
| 4,8 | 0,0480 | 0,0495 | 0,0509 | 0,0522 | 0,0533 | 0,0576 | 0,0616 | 0,0631 | 0,0635 |
| 0,0451 | 0,0466 | 0,0480 | 0,0493 | 0,0504 | 0,0547 | 0,0589 | 0,0606 | 0,0610 | |
| 0,0340 | 0,0353 | 0,0366 | 0,0377 | 0,0388 | 0,0431 | 0,0479 | 0,0500 | 0,0506 | |
| 0,0263 | 0,0275 | 0,0286 | 0,0296 | 0,0306 | 0,0346 | 0,0396 | 0,0421 | 0,0428 | |
| 0,0209 | 0,0219 | 0,0228 | 0,0237 | 0,0246 | 0,0283 | 0,0332 | 0,0359 | 0,0367 | |
| 0,0169 | 0,0178 | 0,0186 | 0,0194 | 0,0202 | 0,0235 | 0,0282 | 0,0310 | 0,0319 | |
| 0,0140 | 0,0147 | 0,0154 | 0,0162 | 0,0167 | 0,0198 | 0,0242 | 0,0270 | 0,0280 |
Влияние площади загрузки. Расчеты напряжений в грунтах показывают, что чем больше площадь передачи нагрузки, тем медленнее происходит затухание (рассеивание на большую площадь) напряжений с глубиной. Это и понятно, так как согласно рис. 45, а, если добавить к нагрузке 7 некоторую нагрузку 2 или 3, то в точке М сжимающее напряжение сг увеличится, но в меньшей степени, чем от нагрузки 1, так как расстояние Р до точки М также увеличится, а с увеличением расстояния величина добавочных напряжений уменьшается.
Рис. 45. Пример влияния размеров загруженной площади на распределение сжимающих напряжений по глубине
Возрастание напряжений с увеличением площади можно установить непосредственно и по данным табл. 9 и проиллюстрировать следующими примерами.
Так, в примере 2 было получено, что на глубине 2 м от ограничивающей полупространство плоскости давление от действия внешней нагрузки интенсивностью р = 3 кГ/см2, распределенной по площади 2X8 ж2, равнялось а2=1,62 кГ/см2. Если при той же интенсивности внешняя нагрузка на поверхность грунта будет действовать по площадке 1X1 м2, то сжимающее напряжение на той же глубине 2 м, учитывая, что в этом случае
На рис. 45, б приведены эпюры распределения сжимающих напряжений по оси нагрузки для двух нагруженных площадей: 2X8 м2 и 1 X 1 м2.
Как видно из приведенных эпюр, при одном и том же внешнем давлении на поверхности напряжения по глубине сильно отличаются, завися от величины площади загрузки.
Таким образом, внешние давления тем медленнее загасают с глубиной, чем больше площадь загрузки, и на любой заданной глубине сжимающие напряжения будут тем больше, чем больше площадь загрузки. Последнее имеет существенное практическое значение. Так, например, слабые слои грунта при большой площади загрузки на некоторой глубине могут испытывать очень большие давления (больше их несущей способности), тогда как при малых площадях загрузки возникающие давления совершенно не повлияют на прочность и устойчивость даже слабого грунта, так как они будут малы по величине. В приведенном на рис. 45, б примере на глубине 3 м от загруженной поверхности под площадкой 2X8 м давление будет около 1,0 кГ/см2, тогда как под площадкой 1X1 м на той же глубине — всего лишь около 0,15 кГ/см2.
Способ элементарного суммирования. Для площадей загрузки сложной формы, которые нельзя разделить на прямоугольники (например, имеющих криволинейное очертание в плане или составленных из треугольников и более сложных фигур), метод угловых точек неприменим.
В этом случае пользуются способом элементарного суммирования, который заключается в следующем. Загрузочную площадь разделяют на площадки таких размеров, чтобы можно было считать приходящиеся на них нагрузки сосредоточенными в их центрах тяжести.
Путем сравнения с результатами точного решения установлено, что при разделении нагруженной поверхности на элементы, длинная сторона которых /о меньше половины расстояния от центра элемента Но до точки, в которой определяется сжимающее напряжение,
погрешность составляет около 6%, т. е. при — = г2 = г3 = гА = = Т
для треугольных элементов »5 = »б =
Рис. 46. К примеру определения сжимающих напряжений по способу элементарного суммирования
Источник
Что такое сжимающая сила?
Свойства материала на растяжение и сжатие представляют собой осевые нагрузки вдоль ортогональных осей. Нагрузки, которые растягиваются на границах системы, описываются как растягивающие нагрузки, в то время как сжатые на границах системы описываются как сжимающие нагрузки.
Внешняя сила, приложенная к телу, деформирует его таким образом, что тело уменьшается в объеме, а длина называется сжимающим напряжением.
Это восстановленная деформация тела при приложении внешней сжимающей нагрузки. Увеличение напряжения сжатия в тонких, длинных цилиндрах имеет тенденцию к разрушению конструкции из-за продольного изгиба колонн. Когда материал не выдерживает сжатие, возникает коробление под напряжением.
Формула напряжения сжатия:
К единице площади прилагается нормальная сила.
Σ = F/A
Где,
Сила сжатия (F): сила сжатия — это нагрузка, необходимая для сжатия материала, чтобы соединить его вместе.
Единица сжимающего напряжения:
Единица СИ такая же, как единица силы для площади.
Итак, он представлен как Н / м2 or Па.
Размер напряжения сжатия:
Размер напряжения сжатия составляет [МЛ-1T-2].
Сжимающее напряжение положительно или отрицательно?
Ответ: сжимающее напряжение отрицательно, поскольку он сжимается, поскольку изменение размера (dL) имеет противоположное направление.
Одинаковы ли предел текучести и прочность на сжатие?
Ответ: Нет, податливость при растяжении и сжатии — это не одно и то же. Значение будет меняться в зависимости от применимости.
Прочность на сжатие:
Это способность материала противостоять сжатию, возникающему из-за сжимающего напряжения. Некоторые материалы могут выдерживать только одно растяжение, некоторые материалы могут выдерживать только сжатие, а некоторые материалы могут выдерживать как растяжение, так и сжатие. Предел прочности на сжатие — это величина, полученная при полном разрушении материала. Испытание на сжатие проводится так же, как испытание на растяжение. Единственная разница в том, что используемая нагрузка — это сжимающая нагрузка.
Прочность на сжатие выше у камня и бетона.
Напряжение сжатия мягкой стали | низкоуглеродистая сталь:
Материал, который подвергается большим деформациям перед разрушением, представляет собой пластичные материалы, такие как мягкий стали, алюминий и его сплавы. Хрупкие материалы, когда подвергается сжимающему напряжению, возникает разрыв из-за внезапного высвобождения накопленной энергии. Принимая во внимание, что когда пластичный материал подвергается сжимающему напряжению, материал сжимается, и деформация происходит без какого-либо разрушения.
Напряжение сжатия и растягивающее напряжение | Напряжение сжатия и растягивающее напряжение
| Сжимающее напряжение | Растягивающее напряжение | |
| Результаты | Последствия сжатия материала в результате сдавливания материала. | Результаты растягивающего напряжения при растяжении материала |
| Толкать или тянуть | В то время как сжимающее напряжение — это давление, оказываемое на тело внешними силами, чтобы изменить его форму и размер. | Напряжение растяжения — это сила, которую тело испытывает от внешних сил, чтобы изменить его форму и размер. |
| Сжатие или удлинение | Напряжение сжатия создается из-за внешней сжимающей силы | Напряжение растяжения возникает из-за того, что сила растяжения стремится к растяжению. |
| Приложение на баре | Когда стержень подвергается сжимающему напряжению, деформации сжимающие (отрицательные). | Когда стержень подвергается растягивающему напряжению, деформации растяжения (положительные). |
Кривая деформации при сжатии
Диаграмма напряжение-деформация: напряжение сжатия
Диаграмма напряжение-деформация для сжатия отличается от растяжения.
При испытании на сжатие кривая напряжения-деформации представляет собой прямую линию до предела упругости. За этой точкой отчетливый изгиб кривой, обозначающий начало пластичности; точка показывает композитный предел текучести при сжатии, который напрямую связан с остаточным напряжением. Увеличение остаточного напряжения увеличивает сжимающее напряжение.
При испытании на сжатие линейная область представляет собой упругую область согласно закону Гука. Следовательно, регион можно представить как
E = модуль Юнга
В этой области материал ведет себя упруго и возвращается в исходное положение за счет снятия напряжения.
Предел текучести:
Это точка, где заканчивается упругость и начинается область пластичности. Таким образом, после достижения предела текучести материал не сможет вернуться в свою фактическую форму после снятия напряжения.
Обнаружено, что если кристаллический материал подвергается сжатию, кривая напряжения-деформации противоположна приложениям растяжения в упругой области. Кривые растяжения и сжатия изменяются при больших деформациях (деформациях), поскольку в сжатом материале происходит сжатие, а при растяжении материал подвергается пластической деформации.
Напряжение-деформация при растяжении | Тест на растяжку:
Линия OA: Пропорциональный предел
Линия OA представляет собой пропорциональный предел. Пропорциональный предел — это предел до тех пор, пока напряжение не станет пропорциональным деформации в соответствии с законом Крюка. По мере увеличения напряжения деформация материала увеличивается.
Точка A: предел упругости:
В этой точке было приложено максимальное напряжение в твердом материале. Эта точка называется пределом упругости. Материал в пределах упругости подвергнется деформации, и после снятия напряжения материал вернется в свое фактическое положение.
Что такое эластопластическая область?
Эластопластическая область:
Это область между пределом текучести и пределом упругости.
Точка B: верхний предел текучести
Пластическая деформация начинается с нарушения его кристаллической структуры. Это смещение становится выше после достижения верхнего предела текучести и ограничивает его движение, эта характеристика известна как деформационное упрочнение.
Точка C: нижний предел текучести
Это точка, после которой проявляются такие характеристики, как деформационное упрочнение. И наблюдается, что за пределами упругости происходит такое свойство, как пластическая деформация.
Постоянная деформация:
Верхний предел текучести:
Точка приложения максимальной нагрузки или напряжения для начала пластической деформации.
Верхний предел текучести нестабилен из-за движения кристаллических дислокаций.
Нижний предел текучести:
Предел минимальной нагрузки или напряжения, необходимый для сохранения пластичности.
Нижний предел текучести является стабильным, поскольку кристаллический материал не движется.
Напряжение — это сопротивление, оказываемое материалом при приложении внешней нагрузки, а деформационное упрочнение — это медленное увеличение сопротивления из-за увеличения дислокаций в материале.
Точка D: точка предельного напряжения
Он представляет собой точку предельного напряжения. Максимальное напряжение может выдержать предельное напряжение. После увеличения нагрузки происходит отказ.
Точка E: точка разрыва
Он представляет собой точку разрыва или разрыва. Когда материал подвергается быстрой деформации после точки предельного напряжения, это приводит к его разрушению. При этом в материале произошла максимальная деформация.
Примеры задач, связанных с напряжением сжатия | Приложения
- Аэрокосмическая и автомобильная промышленность: испытания срабатывания и испытания пружин
- Строительная промышленность: Строительная промышленность напрямую зависит от прочности материалов на сжатие. Столб, кровля, построены с использованием напряжения сжатия.
- Бетонная колонна: в бетонной колонне материал сжимается под действием сжимающего напряжения.
- Материал спрессован, чтобы избежать разрушения здания. Он имеет устойчивое количество напряженной накопленной энергии.
- Косметическая промышленность: уплотнение компактной пудры, подводки для глаз, бальзамов для губ, помады, теней для век производится путем приложения сжимающего усилия.
- Упаковочная промышленность: картонная упаковка, сжатые бутылки, ПЭТ-бутылки.
- Фармацевтическая промышленность: в фармацевтической промышленности в основном используется сжимающее напряжение.
- Разрушение, уплотнение, крошка происходит при изготовлении таблеток. Твердость и прочность на сжатие — важная часть фармацевтической промышленности.
- Спортивная индустрия: мяч для крикета, теннисный мяч, баскетбольный мяч сжаты, чтобы сделать его более жестким.
Как измерить сжимающее напряжение?
Испытание на сжатие:
Испытание на сжатие — это определение поведения материала при сжимающей нагрузке.
Испытание на сжатие обычно используется для камня и бетона. Испытание на сжатие показывает напряжение и деформацию материала. Экспериментальный результат должен подтвердить теоретические выводы.
Виды компрессионного тестирования:
- Испытание на изгиб
- Весенний тест
- Испытание на раздавливание
Испытание на сжатие предназначено для определения параметров целостности и безопасности материала путем выдерживания сжимающего напряжения. Также обеспечивается сохранность готовой продукции, комплектующих, изготавливаемого инструмента. Он определяет, подходит ли материал для этой цели и соответствующим образом изготовлен.
Тесты сжатия предоставляют данные для следующих целей:
- Для измерения качества партии
- Чтобы понять последовательность в производстве
- Помочь в процедуре проектирования
- Уменьшить цену материала
- Гарантировать качество по международным стандартам и т. Д.
Машина для испытания на сжатие:
Машины для испытания на сжатие включают измерения таких свойств материала, как модуль Юнга, предел прочности на сжатие, предел текучести и т. Д., Следовательно, общие статические характеристики прочности материалов на сжатие.
Устройство сжатия сконфигурировано для множества приложений. Благодаря конструкции машины он может выполнять испытания на растяжение, циклическое испытание на сдвиг и изгиб.
Испытание на сжатие проводится так же, как испытание на растяжение. В обоих тестах происходит только изменение нагрузки. В машинах для испытания на растяжение используются растягивающие нагрузки, а в машинах для испытания на сжатие — сжимающие нагрузки.
Прочность на сжатие различных материалов:
· Прочность бетона на сжатие: 17Мпа-27МПа
· Прочность стали на сжатие: 25 МПа
· Прочность гранита на сжатие: 70-130 МПа
· Прочность цемента на сжатие: 11.5 — 17.5 МПа.
· Предел текучести алюминия при сжатии: 280 МПа
Какое допустимое напряжение сжатия для стали?
Ответ: Допустимые напряжения обычно измеряются кодами конструкции этого металла, такого как сталь и алюминий. Он представлен долей его предельного напряжения (прочности).
Какова прочность бетона на сжатие в разном возрасте?
это минимальное сжатие сила была материальной в стандартном испытании 28-дневного бетонного цилиндра.
Измерения прочности бетона на сжатие требуют от 28 до 35 МПа через 28 дней.
Прочность бетона на сжатие:
Проблемы с компрессионным напряжением:
Проблема #1
Стальной стержень диаметром 70 мм и длиной 3 м окружен оболочкой из чугуна толщиной 7 мм. Рассчитайте сжимающую нагрузку для комбинированного стержня 0.7 мм на длине 3 м. (Eстали = 200 ГПа, а Eчугун = 100 ГПа.)
Решение:
δ=PL/AE
δ=δ чугун=δ стали= 0.7мм
δ чугун ={4}*{100 000}*{84^{2}-70^{2} = 0.7
P чугун = 50306.66 πN
δ сталь= л (3000)} { гидроразрыва { пи} {4} * {200 000}*{70^{2}= 0.7
P стали= 57166.66πN
ΣFV=0
P= P чугун +P стали
P= 50306.66π+57166.66π
P= 107473.32πN
P= 337.63 кН
Проблема #2:
Статуя весом 10 кН покоится на плоской поверхности на вершине столба высотой 6.0 м. Площадь поперечного сечения башни 0.20 м.2 и выполнен из гранита плотностью 2700кг / м3. Рассчитайте сжимающее напряжение и деформацию в поперечном сечении на 3 м ниже верха башни и верхнего сегмента соответственно.
решение:
Объем сегмента башни с высотой
H= 3.0 м и площадь поперечного сечения A= 0.2м2
V = A * H = 0.3 * 0.2 = 0.6 м ^ 3
Плотность ρ= 2.7 × 10 ^ 3 кг / м3, (графит)
Масса сегмента башни
m= ρV =(2.7×10^3 *0.60m3)=1.60×10^3 kg.
Вес сегмента башни составляет
Wp = mg= (1.60 × 103 * 9.8) = 15.68 кН.
Вес скульптуры
Ws = 10 кН,
нормальная сила на 3 м ниже скульптуры,
F⊥ = wp + ws = (1.568 + 1.0) × 104 Н = 25.68 кН.
Следовательно, напряжение рассчитывается по формуле F/A
= 2.568 × 104 * 0.20
= 1.284 × 10 ^ 5 Па = 128.4 кПа.
Y=4.5×10^10Pa = 4.5×10^7kPa.
Таким образом, деформация сжатия, рассчитанная в этом положении, равна
Y= 128.4 / 4.5 × 107
= 2.85 × 10-6.
Проблема #3:
Стальной стержень изменяемого поперечного сечения подвергается опасности осевого усилия. Найдите значение P для равновесия.
E = 2.1 * 10 ^5MPa. L1=1000mm, L2=1500mm, L3=800mm.A1=500mm2, A2 = 1000 мм2, A3 = 700 мм2.
Из равновесия:
ΣFx = 0
+ 8000-10000 + П-5000 = 0
P = 7000N
Дополнительные статьи нажмите здесь.
Если
известно угловое сжимающее напряжение,
то по нему легко определяются и сжимающие
напряжения для любой точки полупространства,
загруженного равномерно распределенной
нагрузкой, приложенной по прямоугольной
площади. Для этого используется метод
угловых точек. Здесь могут встретиться
следующие три случая:
1)
Точка М
находится на контуре прямоугольника,
и величина z
определяется как сумма двух угловых
напряжений для загруженных прямоугольников
I
и II
(рис.3.12,а):
.
(3.24)
2)
Точка М
находится внутри прямоугольника, и
величина z
определяется как сумма четырех угловых
напряжений прямоугольников I,
II,
III
и IV
(рис.3.12,б):
.
(3.25)
Р
Схема разбивки нагруженной площади при
определении сжимающих напряжений по
методу угловых точек
3)
Точка М
расположена вне прямоугольника, и
величина z
определяется как сумма угловых напряжений
прямоугольников III
и IV,
взятых со знаком минус, и угловых
напряжений I
и II
со знаком плюс (рис.3.12,в); для этого
последнего случая напряжения для всех
горизонтальных площадок по вертикали,
проходящей через точку М,
будут равны:
,
(3.26)
где
P
– интенсивность внешней равномерно
распределенной нагрузки;
–угловые
коэффициенты, определяемые по таблице
в зависимости от отношений
и
для каждого рассматриваемого
прямоугольника (табл.II.2
приложения II).
Метод угловых
точек широко используется для определения
взаимного влияния смежных фундаментов
на деформацию их оснований.
3.3.2. Влияние формы и площади загрузки
Расчеты
показывают, что при одинаковых удельных
нагрузках напряжения при большей площади
загрузки затухают медленнее и
распространяются на большую глубину.
На
рис.3.13 показано влияние формы и размеров
загруженной площади на распределение
сжимающих напряжений по глубине.
Рис.3.13. Характер
распределения напряжений zпо оси фундамента в зависимости от формы
и площади его подошвы: 1 – для квадратного
фундамента; 2 – для ленточного фундамента
ширинойb= 1 м; 3 – для
ленточного фундамента ширинойb= 2 м
Как
видно из приведенных эпюр, при одном и
том же внешнем давлении на поверхности
напряжения с глубиной сильно отличаются
друг от друга, так как они зависят от
формы и площади загрузки.
Соседние файлы в папке Механика грунтов лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Формула для расчета абсолютных деформаций
Расчет перемещения сечений
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Сжимающее напряжение
Предмет
Материаловедение
Разместил
🤓 nataliya.veselova.1961
👍 Проверено Автор24
напряжение, возникающее в результате действия сжимающей нагрузки.
Научные статьи на тему «Сжимающее напряжение»
Расчет осадок фундамента методом послойного суммирования
В случае применения данного метода рассматривается сжимаемая толща грунта, которая испытывает нагрузки…
от вертикальных напряжений….
Сжимаемая толща рассматривается как линейно-деформируемая среда, а условием, ограничивающим деформации…
на границе слоя;
определяем полное вертикальное напряжение;
разбиваем толщу на элементарные слои и ведем…
расчет осадок в пределах сжимаемого слоя, значения для каждого слоя записывают в табличной форме;
оцениваем

Статья от экспертов
Распределение сжимающих напряжений в основании из мерзлого торфа
Рассмотрена методика расчета напряженно-деформированного состояния оснований из мерзлого торфа (или грунта) с учетом нелинейности его модуля деформации.
Расчет осадок фундаментов
имеющий толщину 0,2-0,4 от ширины фундамента в пределах которого просто найти деформации, возникающие от сжимаемых…
Затем вычисляется напряжение от собственного веса грунта на границе основных слоев и строится эпюра напряжений…
Затем определяют напряжение от собственного веса на нижней границе и дополнительное вертикальное напряжение…
Вертикальное напряжение определяется для каждого элементарного слоя;
определяют границы сжимаемой зоны…
Таким образом находят границу сжимаемой толщи и осадку основания.

Статья от экспертов
Устойчивость пластин цементита при воздействии сжимающих напряжений
The behaviour of steels with a structure of plate cementite in requirements of cold plastic deformation is examined. At the effect of compression stress there are losses of stability of plates. Despite the major width being much of cementite, plates remain unbroken. Such behaviour of carbides is explained by their laminate structure.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек