Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
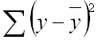
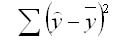
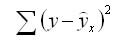
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
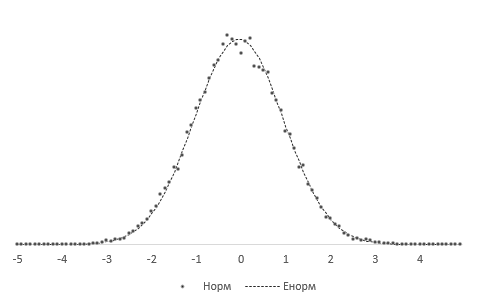
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
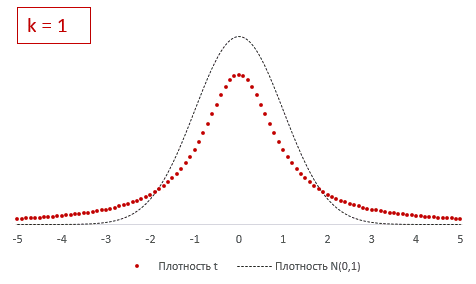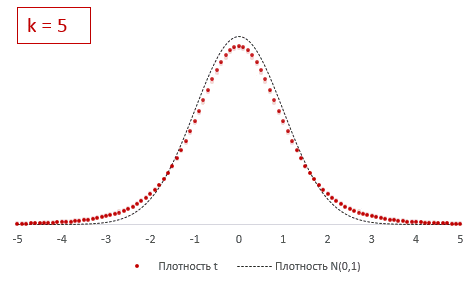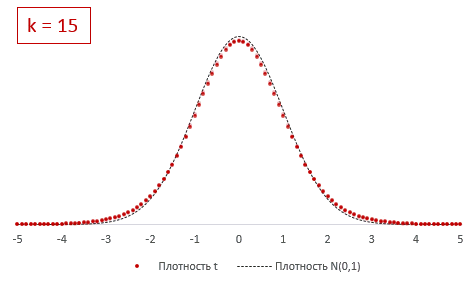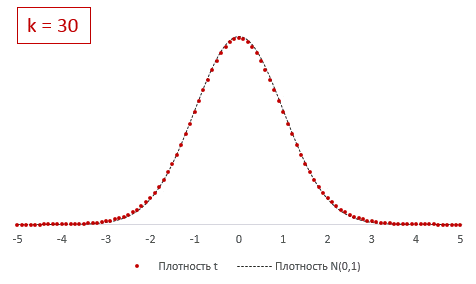
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
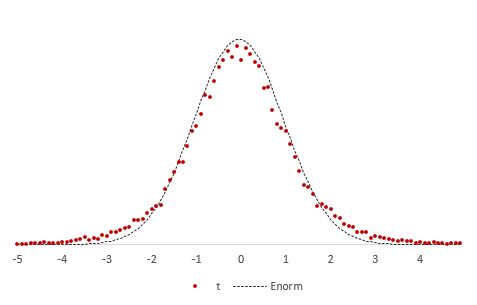
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
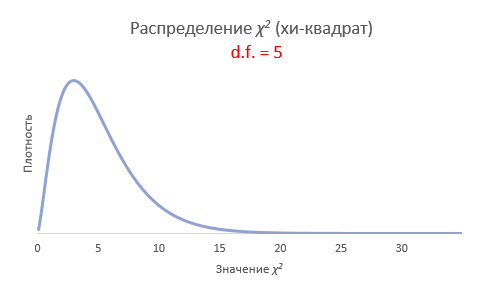
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
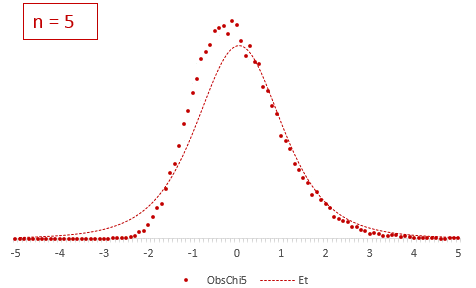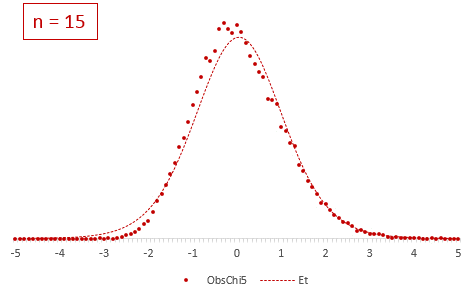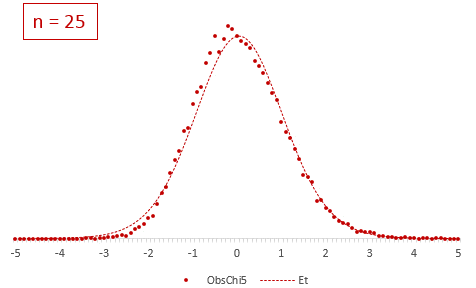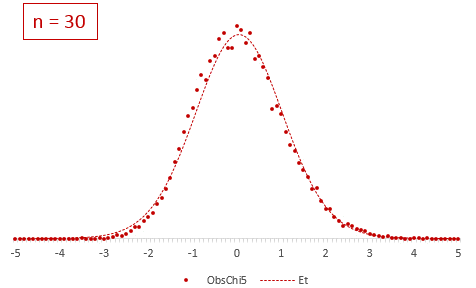
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
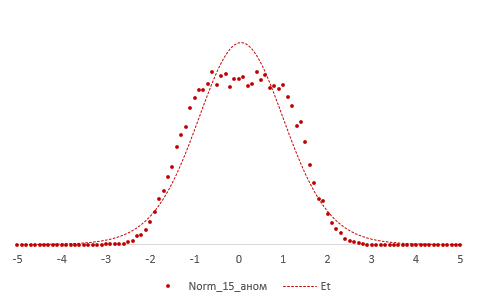
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
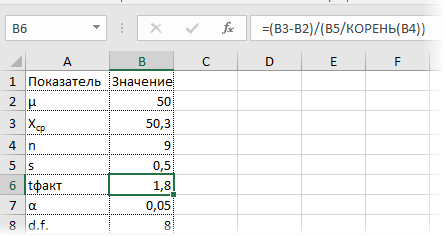
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
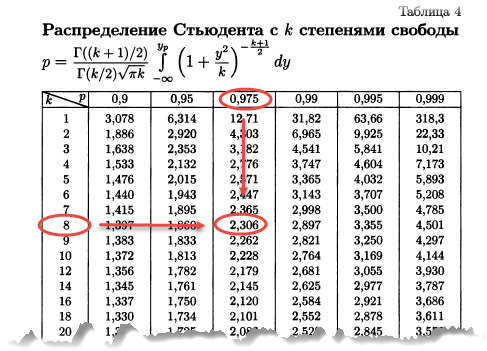
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
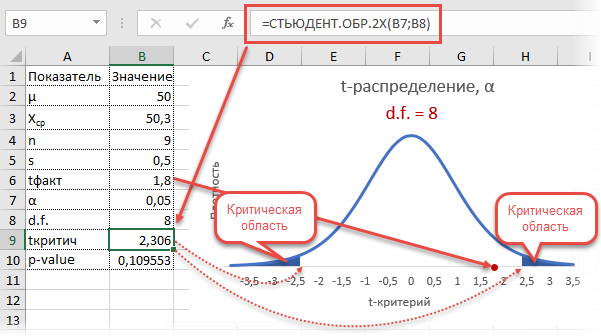
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
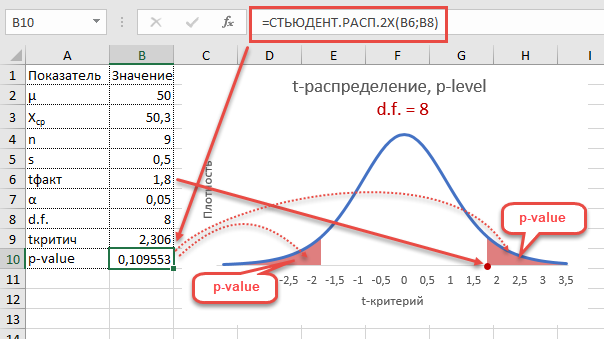
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
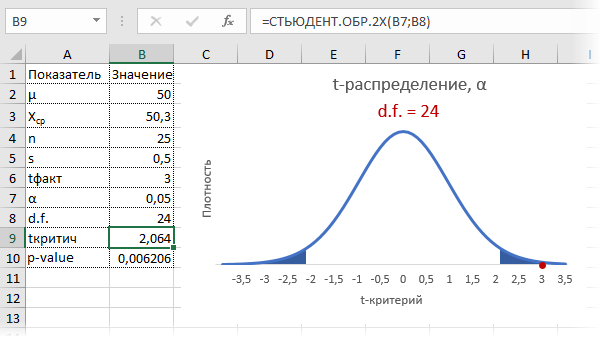
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
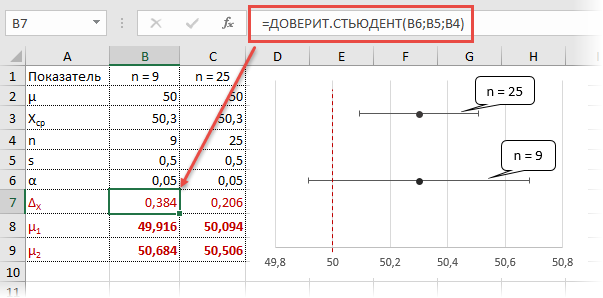
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
В этом руководстве объясняется, как читать и интерпретировать таблицу t-Distribution .
Что такое таблица t-распределения?
Таблица t-распределения — это таблица, которая показывает критические значения t-распределения. Чтобы использовать таблицу t-распределения, вам нужно знать только три значения:
- Степени свободы t-критерия
- Количество хвостов t-теста (односторонний или двусторонний)
- Альфа-уровень t-теста (обычно выбирают 0,01, 0,05 и 0,10).
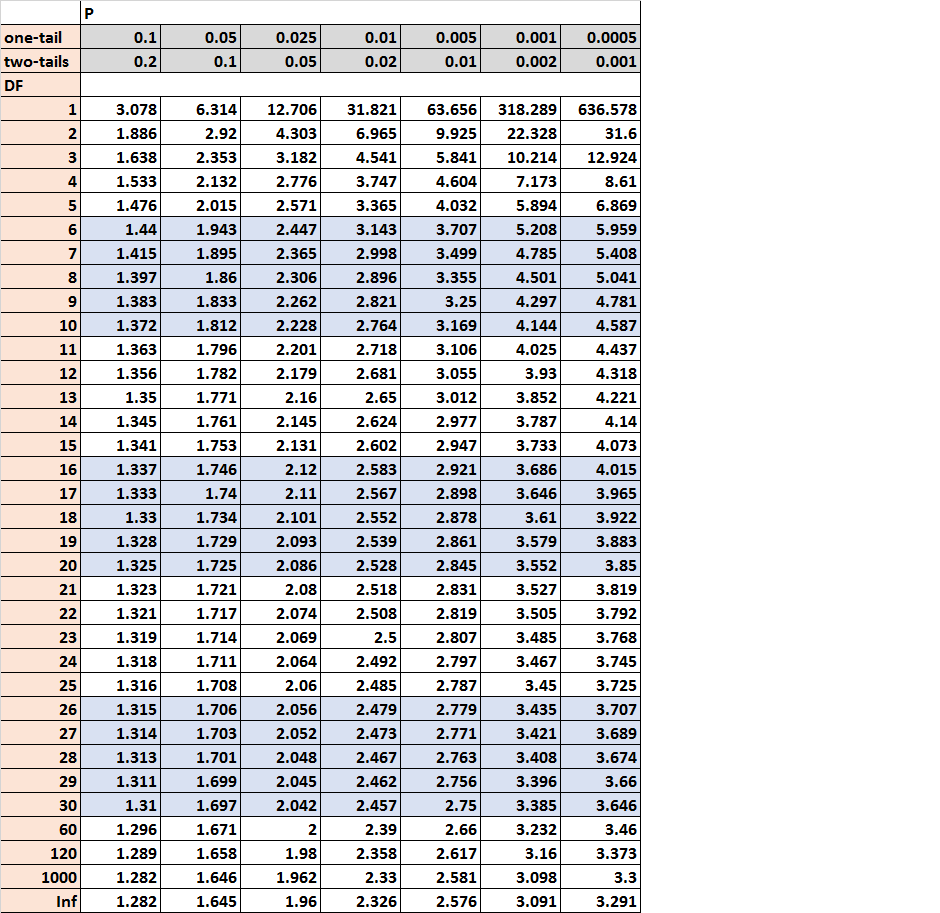
Вот пример таблицы t-Distribution со степенями свободы, указанными в левой части таблицы, и альфа-уровнями, указанными в верхней части таблицы:
Когда вы проводите t-тест, вы можете сравнить статистику теста из t-теста с критическим значением из таблицы t-распределения. Если статистика теста больше критического значения, найденного в таблице, то вы можете отклонить нулевую гипотезу t-критерия и сделать вывод, что результаты теста статистически значимы.
Давайте рассмотрим несколько примеров использования таблицы t-Distribution.
Примеры использования таблицы t-распределения
В следующих примерах показано, как использовать таблицу t-Distribution в нескольких различных сценариях.
Пример № 1: Односторонний t-критерий для среднего
Исследователь набирает 20 субъектов для исследования и проводит односторонний t-критерий для среднего значения, используя альфа-уровень 0,05.
Вопрос: после того, как она проведет свой односторонний t-критерий и получит тестовую статистику t , с каким критическим значением она должна сравнить t ?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 20-1 = 19. Задача также сообщает нам, что она проводит односторонний тест и использует альфа-уровень 0,05, поэтому соответствующее критическое значение в таблице t-распределения равно 1,729 .
Пример № 2: Двусторонний t-критерий для среднего
Исследователь набирает 18 субъектов для исследования и проводит двусторонний t-критерий для среднего значения, используя альфа-уровень 0,10.
Вопрос: После того, как она проведет свой двусторонний t-критерий и получит тестовую статистику t , с каким критическим значением она должна сравнить t ?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 18-1 = 17. Задача также сообщает нам, что она проводит двусторонний тест и использует альфа-уровень 0,10, поэтому соответствующее критическое значение в таблице t-распределения равно 1,74 .
Пример №3: Определение критического значения
Исследователь проводит двусторонний t-критерий для среднего значения, используя размер выборки 14 и альфа-уровень 0,05.
Вопрос: Каким должно быть абсолютное значение ее тестовой статистики t , чтобы она отвергла нулевую гипотезу?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 14-1 = 13. Задача также сообщает нам, что она проводит двусторонний тест и использует альфа-уровень 0,05, поэтому соответствующее критическое значение в таблице t-распределения равно 2,16.Это означает, что она может отклонить нулевую гипотезу, если тестовая статистика t меньше -2,16 или больше 2,16.
Пример №4: Сравнение критического значения с тестовой статистикой
Исследователь проводит правосторонний t-критерий для среднего значения, используя размер выборки 19 и альфа-уровень 0,10.
Вопрос: Тестовая статистика t оказывается равной 1,48. Может ли она отвергнуть нулевую гипотезу?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 19-1 = 18. Задача также сообщает нам, что она проводит правосторонний тест (который является односторонним тестом) и что она использует альфа-уровень 0,10, поэтому соответствующее критическое значение в таблице t-распределения равно 1,33.Поскольку ее тестовая статистика t больше 1,33, она может отклонить нулевую гипотезу.
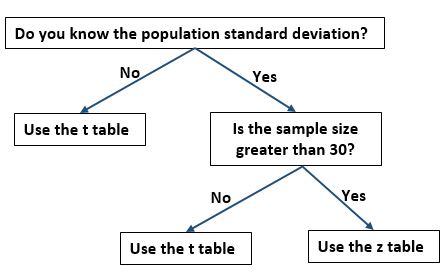
Должны ли вы использовать таблицу t или таблицу z?
Одной из проблем, с которой часто сталкиваются учащиеся, является определение того, следует ли им использовать таблицу t-распределения или таблицу z для нахождения критических значений для конкретной задачи. Если вы застряли на этом решении, вы можете использовать следующую блок-схему, чтобы определить, какую таблицу вам следует использовать:
Дополнительные ресурсы
Полный список таблиц критических значений, включая таблицу биномиального распределения, таблицу распределения хи-квадрат, z-таблицу и другие, см. на этой странице .
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Использование критерия Стьюдента для проверки значимости параметров регрессионной модели
Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:
где P — значение параметра;
Sp — стандартное отклонение параметра.
Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N—k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).
Если вычисленное значение tp выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.
Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.
Конспект курса «Основы статистики»
1. Введение
Генеральная совокупность — множество всех объектов, относительно которых предполагается делать выводы при изучении конкретной задачи.
Выборка — часть генеральной совокупности, которая охватывается экспериментом.
Репрезентативная выборка — выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.
Унимодальное распределение — распределение, имеющее только одну моду (пример: нормальное распределение)
Способы формирования репрезентативной выборки:
Простая случайная выборка (simple random sample)
Стратифицированная выборка (stratified sample)
Групповая выборка (cluster sample)
Типы переменных:
непрерывные (рост в мм)
дискретные (количество публикаций у учёного)
Ранговые (успеваемость студентов)
Гистограмма частот:
Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.
Описательные статистики:
Меры центральной тенденции (узкий диапазон, высокие значения признака):
Мода (mode) — значение во множестве наблюдений, которое встречается наиболее часто.
Медиана (median) — значение признака, которое делит упорядоченное множество пополам.
Среднее значение (mean, среднее арифметическое) — сумма всех значений измеренного признака, делённая на количество измеренных значений.
( используется для среднего значения из выборки, а для генеральной совокупности латинская буква )
Свойства среднего:
Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.
Если каждое значение выборки умножить на определённое число, то и среднее значение увеличится в это число раз.
Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.
Меры изменчивости (широкий диапазон, вариативность признака):
Размах (range) — разность максимального и минимального значения.
При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.
Дисперсия (variance) — средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия генеральной совокупности:
(среднеквадратическое отклонение генеральной совокупности)
(среднеквадратическое отклонение выборки)
Свойства дисперсии:
Квартили распределения и график box-plot
Квартили — три точки (значения признака), которые делят упорядоченное множество данных на четыре равные части.
Box-plot — такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы.
Нормальное распределение
Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.
Стандартизация
Стандартизация или z-преобразование — преобразование полученных данных в стандартную Z-шкалу (Z-scores) со средним и
Правило «двух» и «трёх» сигм
Центральная предельная теорема
Центральная предельная теорема — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.
Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .
Стандартная ошибка среднего — теоретическое стандартное отклонение всех средних выборки размера , извлекаемое из совокупности.
30″ alt=»SE = frac<sqrt>, n>30″ src=»https://habrastorage.org/getpro/habr/upload_files/20c/135/3bc/20c1353bcfedf2ff8851752cf7f49f37.svg»/>
Доверительные интервалы для среднего
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).
Идея статистического вывода
P-значение (P-value) — величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода).
2. Сравнение средних
T-распределение
Если число наблюдений невелико и sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).
Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от
«Форма» распределения определяется числом степеней свободы ().
С увеличением числа распределение стремится к нормальному.
t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.
Сравнение двух средних; t-критерий Стьюдента
Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.
Условия для корректности использования t-критерия Стьюдента:
Две независимые группы
Формула стандартной ошибки среднего:
Формула числа степеней свободы:
Формула t-критерия Стьюдента:
Переход к p-критерию:
Проверка распределения на нормальность, QQ-Plot
Однофакторный дисперсионный анализ
Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.
Незвисимая переменная — номинативная перменная с нескольким градациями, разделяющая наблюдения на группы.
Зависимая перемнная — количественная переменная, по степени выраженности которой сравниваются группы.
1
2
3
Группы:
Нулевая гипотеза:
Альтернативная гипотеза:
Среднее значение всех наблюдений:
Общая сумма квадратов (Total sum of sqares):
Показатель, который характеризует насколько высока изменчивость данных, без учёта разделения их на группы.
Число степеней свободы:
— Межгрупповая сумма квадратов (Sum of sqares between groups)
— Внутригрупповая сумма квадратов (Sum of sqares within groups)
F-значение (основной статистический показатель дисперсионного анализа):
Межгрупповой средний квадрат — усредненное значение межгрупповой суммы квадратов.
При делении значения межгрупповой суммы квадратов на число степеней свободы, полученный показатель усредняется.
Внутригрупповой средний квадрат — отношение внутригрупповой суммы квадратов к числу степеней свободы.
Поэтому формула F-значения часто записывается:
Множественные сравнения в ANOVA
Проблема множественных сравнений:
Чем больше статистических гипотез проверяется на одних и тех же данных, тем вероятнее ошибка первого рода — заключение о наличии различий между группами, тогда как на самом деле верна нулевая гипотеза об отсутствии различий.
Поправка Бонферрони
Самый простой (и консервативный) метод: P-значения умножаются на число выполненных сравнений.
Критерий Тьюки
Критерий Тьюки используется для проверки нулевой гипотезы против альтернативной гипотезы , где индексы и обозначают любые две сравниваемые группы.
Указанные сравнения выполняются при помощи критерия Тьюки, который представляет собой модифицированный критерий Стьюдента:
Отличие от критерия Стьюдента заключается в том, как рассчитывается стандартная ошибка $SE$:
где — рассчитываемая в ходе дисперсионного анализа внутригрупповая дисперсия.
Многофакторный ANOVA
При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.
Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.
Условия применения двухмерного дисперсионного анализа:
Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.
Выборки должны быть независимыми.
Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.
Группы должны иметь одинаковый объем выборки.
АБ тесты и статистика
АБ тестирование — это проведение экспериментов при помощи статистики, пожалуй, самый яркий пример того, зачем статистика нужна в реальной жизни. Этот метод маркетингового исследования заключается в том, что контрольная группа элементов сравнивается с набором тестовых групп, где один или несколько показателей изменены для того, чтобы выяснить, какие из изменений улучшают целевой показатель. Например, мы можем поменять цвет кнопки для регистрации с красного на синий и сравнить, насколько это будет эффективно.
3. Корреляция и регрессия
Понятие корреляции
Корреляция — статистическая взаимосвязь двух или более случайных величин. При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.
Принимает значения [-1, 1]
— показатель силы и направления взаимосвязи двух количественных переменных.
Знак коэффициента корреляции показывает направление взаимосвязи.
Коэффициент детерминации
— показывает, в какой степени дисперсия одной переменной обусловлена влиянием другой переменной.
Равен квадрату коэффициента корреляции.
Принимает значения [0, 1]
Условия применения коэффициента корреляции
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:
Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
Распределения переменных и должны быть близки к нормальному.
Число варьирующих признаков в сравниваемых переменных и должно быть одинаковым.
Коэффициент корреляции Спирмена
Коэффициент ранговой корреляции Спирмена — это количественная оценка статистического изучения связи между явлениями, используемая в непараметрических методах.
Регрессия с одной независимой переменной
Уравнение прямой:
— (intersept) отвечает за то, где прямая пересекает ось y.
— (slope) отвечает за направление и угол наклона, образованный с осью x.
Метод наименьших квадратов
МНК — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов остатков была минимальна.
Формула нахождения остатка:
— остаток
— реальное значение
— значение, которое предсказывает регрессионная прямая
Сумма квадратов всех остатков:
Параметры линейной регрессии:
Гипотеза о значимости взаимосвязи и коэффициент детерминации
Коэффициенты линейной регрессии
Коэффициенты регрессии (β) — это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой.
Коэффициент детерминации
— доля дисперсии зависимой переменной (Y), объясняем регрессионной моделью.
— сумма квадратов остатков
— сумма квадратов общая
Условия применения линейной регрессии с одним предиктором
Линейная взаимосвязь и
Нормальное распределение остатков
Гомоскедастичность — постоянная изменчивость остатков на всех уровнях независимой переменной
Регрессионный анализ с несколькими независимыми переменными
Множественная регрессия (Multiple Regression)
Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависимую.
Требования к данным
линейная зависимость переменных
нормальное распределение остатков
проверка на мультиколлинеарность
нормальное распределение переменных (желательно)
http://www.chem-astu.ru/science/reference/student.html
http://habr.com/ru/post/591023/
11
ГОСУДАРСТВЕННОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ
УНИВЕРСИТЕТ»
Кафедра
«Автоматизированные системы управления»
Эконометрика
и экономико-математические
методы и модели
Методические
указания
к лабораторным и
практическим занятиям для студентов
специальностей
1-25 01 04 «Финансы и кредит»,
1-25 01 08 «Бухгалтерский
учет, анализ и аудит»,
1-25 01 10 «Коммерческая
деятельность»
Часть 1
Могилев 2012
У
004.65
ББК 32.81
Э 11
Рекомендовано к
опубликованию
учебно-методическим
управлением
ГУ ВПО
«Белорусско-Российский университет»
Одобрено кафедрой
«Автоматизированные системы управления»
«20» марта 2012 г., протокол № 7
Составитель: канд.
техн. наук, доц. Т. В. Мрочек
Рецензент канд.
техн. наук, доц. В. А. Широченко
Описаны основные
этапы выполнения лабораторных и
практических работ по первой части
изучаемой дисциплины – эконометрике.
Приведены основные понятия, расчетные
зависимости и примеры выполнения
наиболее распространенных задач по
рассматриваемым темам.
Учебное издание
Эконометрика и
экономико-математические методы
и модели
Ответственный за
выпуск С. К. Крутолевич
Технический
редактор А. Т. Червинская
Компьютерная
верстка И. А. Алексеюс
Подписано в печать . Формат 60х84/16.
Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.-печ. л. .
Уч.-изд. л. . Тираж 66 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего
профессионального образования
«Белорусско-Российский университет»
ЛИ № 02330/375 от 29.06.2004 г.
212000, Г. Могилев, пр. Мира, 43
© ГУ ВПО «Белорусско-Российский
университет», 2012
1 Парная регрессия и корреляция
Цель: определение
характеристик уравнений парной линейной
и нелинейной регрессий, оценка значимости
параметров и корреляции и выбор наилучшего
уравнения регрессии.
1.1 Расчетные формулы
Регрессия –
это модель вида
,
где y
– зависимая
переменная (результативный признак,
функция отклика, эндогенная (внутренняя)
переменная). Термин «внутренний» отражает
тот факт, что значения зависимой
переменной у
определяются
только значениями независимых переменных
x;
х –
независимая переменная (объясняющая
переменная, фактор, входная переменная,
внешняя или экзогенная переменная).
Термин «внешний» говорит о том, что
значения переменных х
определяются
вне рассматриваемой модели, для которой
они являются заданными.
Знак «ˆ»
(«ридж») означает, что между переменными
х и
у
нет строгой функциональной зависимости,
поэтому практически в каждом отдельном
случае величина у
складывается из двух слагаемых:
,
где у
– фактическое (экспериментальное)
значение результативного признака;
–теоретическое
значение результативного признака,
найденное из уравнения регрессии;
–случайная
величина, характеризующая отклонения
фактического значения у
от
.
Случайная величина
i
включает влияние не учтенных в модели
факторов, случайных ошибок и особенностей
измерения [5, с. 44].
В
случае единственной входной переменной
регрессию называютпарной
(простой),
если переменных
две и более –множественной.
В зависимости от
типа выбранного уравнения различают
линейную и
нелинейную
регрессию
(экспоненциальную, логарифмическую и
т. д.).
При изучении
регрессии выполняют следующие этапы:
-
спецификация
уравнения регрессии
и определение параметров регрессии;
-
определение
степени стохастической взаимосвязи
результативного признака и факторов,
проверка общего качества уравнения
регрессии; -
проверка
статистической значимости каждого
коэффициента уравнения регрессии и
определение их доверительных интервалов.
Спецификация
уравнения регрессии – это выбор вида
аналитической зависимости
.
В случае парной регрессии спецификация
осуществляется по графическому
изображению реальных статистических
данных в виде точек в декартовой системе
координат, которое называется
корреляционным
полем
(диаграммой рассеивания) (рисунок 1.1).
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем в большей мере теоретические
значения результативного признака
подходят к фактическим даннымy.
Парная регрессия
применяется, если имеется доминирующий
фактор, который и используется в качестве
объясняющей переменной х.
Простейшей является
линейная
взаимосвязь
между x
и y,
описываемая линейной функцией регрессии
вида
.
Для вычисления
коэффициентов a,
b
используется метод
наименьших квадратов
(МНК), который позволяет получить
такие оценки параметров а
и b,
при которых
сумма квадратов отклонений фактических
значений зависимой переменной у
от теоретических
минимальна, т. е.
Это означает, что
линейная регрессия на диаграмме
рассеивания будет проходить «достаточно
близко» к точкам (xi,
yi).
Теснота
связи изучаемых явлений оценивается
при использовании линейной регрессии
с помощью линейного
коэффициента корреляции
.
Линейный коэффициент
корреляции
принимает значение в пределах от (–1)
до 1, т. е. (–1) < rху
< 1. Чем ближе
к единице,
тем связь теснее.
Качественная
оценка тесноты связи величин x
и y
может быть выявлена на основе шкалы
Чеддока.
Линейный
коэффициент корреляции
характеризует
степень тесноты не всякой, а только
линейной зависимости. При нелинейной
зависимости между явлениями линейный
коэффициент корреляции теряет смысл,
и для измерения тесноты связи применяют
так называемый индекс
корреляции
.
Для оценки
качества подбора линейной регрессии
рассчитывается квадрат линейного
коэффициента корреляции, называемый
коэффициентом
детерминации
,
а для нелинейной регрессии – квадрат
индекса корреляции, называемыйиндексом
детерминации
.
Коэффициент
детерминации характеризует долю
дисперсии
результативного признакаy,
объясняемую регрессией, в общей дисперсии
результативного признака. Чем больше
доля объясненной вариации, тем меньше
роль прочих факторов и тем лучше уравнение
регрессии описывает исходные данные.
Чем ближеR2
к 1, тем лучше
модель описывает (аппроксимирует)
исходные данные, и, значит, ее можно
использовать для оценки качества
построенной модели.
Средняя ошибка
аппроксимации
– среднее
отклонение расчётных значений от
фактических. Построенное уравнение
регрессии считается хорошего качества,
если значение
не превышает
8–10 % [5, с.
107].
Средний коэффициент
эластичности
показывает,
на сколько процентов в среднем изменится
результат у
от своей
средней величины при изменении фактора
х на
1 % от своего среднего значения:
,
где
– первая
производная уравнения регрессии,
характеризующая соотношение приростов
результата у
и фактора х.
После того, как
найдено уравнение линейной регрессии,
проводится:
1) оценка
значимости уравнения в целом с помощью
F-критерия
Фишера;
2) оценка
значимости коэффициентов регрессии с
помощью t-критерия
Стьюдента.
F-критерий
Фишера дает
ответ на вопрос, при каких значениях R2
уравнение
регрессии следует считать статистически
незначимым, что делает необоснованным
его использование. Согласно F-критерию
Фишера, выдвигается «нулевая» гипотеза
Н0
о
статистической
незначимости уравнения регрессии (т.
е. о статистически незначимом отличии
величины F
от нуля).
Если расчетное значение F-критерия
превышает табличное
,
т. е.
,
то гипотеза
Н0
отклоняется
и принимается статистическая значимость
и надежность уравнения регрессии. Если
,
то гипотеза Н0
не отклоняется
и признается статистическая незначимость,
ненадежность уравнения регрессии.
Табличное значение
F-критерия
определяется
по таблицам F-критерия
Фишера при числе степеней свободы
m
(m
– число
параметров при переменных х),
(n
– число наблюдений) и заданному уровню
значимости α.
Уровнем значимости
α
в статистических гипотезах называется
вероятность отвергнуть верную гипотезу.
Уровень значимости α
обычно принимает значения 0,05 и 0,01, что
соответствует вероятности отвергнуть
верную гипотезу 5 и 1 %.
Возможна ситуация,
когда часть вычисленных коэффициентов
регрессии не обладает необходимой
степенью значимости, т. е. значения этих
коэффициентов будут меньше их стандартной
ошибки. В этом случае такие коэффициенты
должны быть исключены из уравнения
регрессии. Поэтому проверка адекватности
построенного уравнения регрессии,
наряду с проверкой значимости коэффициента
детерминации R2,
включает в
себя также и проверку значимости каждого
коэффициента регрессии.
Для оценки
статистической значимости коэффициентов
регрессии применяется t-критерий
Стьюдента,
согласно которому выдвигается «нулевая»
гипотеза Н0
о статистической
незначимости коэффициента уравнения
регрессии (т. е. о статистически
незначимом отличии a
и b
от нуля). Эта
гипотеза отвергается при выполнении
условия
,
при этом принимается статистическая
значимость и надежность проверяемого
коэффициента регрессии, т. е. считается,
что отличие рассматриваемого коэффициента
уравнения регрессии от нуля статистически
значимо. Табличное значениеt-критерия
определяется
по таблице t-критерия
Стьюдента по числу степеней свободы
и заданному уровню значимости α. Расчетные
значения-критерия
для каждого коэффициента регрессии
(-статистики
Стьюдента) представляют собой отношение
оценки коэффициента регрессии к его
стандартной ошибке.
Стандартные
ошибки коэффициентов
линейной регрессии позволяют получить
представление о точности полученных
оценок коэффициентов регрессии
и
,
о том, насколько далеко они могут
отклониться от истинных значений
коэффициентов.
Общая
дисперсия
результативного
признака у
отображает
влияние как основных, так и остаточных
факторов. Остаточная
дисперсия
результативного
признака у
отображает
влияние только остаточных факторов.
Рассчитанные
значения оценок коэффициентов регрессии
являются приближенными, полученными
на основе имеющихся выборочных данных.
Для оценки того, насколько точные
значения оценок коэффициентов могут
отличаться от рассчитанных, осуществляется
построение доверительных интервалов.
Доверительные интервалы определяют
пределы, в которых лежит точное значение
определяемого показателя с заданной
вероятностью
[1,
с. 131].
Доверительные
интервалы для оценок коэффициентов
линейной регрессии рассчитываются по
формулам:
,
,
где
,
– предельные ошибки, рассчитываемые
по формулам
,
.
В таблице 1.1
представлены формулы для вычисления
основных характеристик линейной и
различных нелинейных регрессий.
В
MS
Excel
для построения функции линейной регрессии
используются команда «Добавить линию
тренда» и инструмент анализа «Регрессия».
Таблица 1.1 – Основные
характеристики
линейной и различных нелинейных регрессий
|
Функция |
линейная |
логарифмическая |
степенная |
экспоненциальная |
|
Среднеквадратические |
|
|||
|
Линейный |
(–1) < rху< 1 |
– |
||
|
Индекс корреляции |
– |
|
||
|
Коэффициент детерминации |
|
– |
||
|
Индекс детерминации |
– |
|
||
|
Табличное |
|
|||
|
Расчетное |
|
|||
|
Средняя |
|
|||
|
Коэффициент |
|
|
|
|
|
Общая |
|
|||
|
Остаточная |
|
|||
|
Стандартная ошибка коэффициента |
|
|||
|
Стандартная ошибка коэффициента |
|
|||
|
Расчетные значения
|
a |
|
||
|
b |
|
|||
|
Табличное |
|
Для построения
функций линейной и нелинейной регрессий
используется команда «Добавить линию
тренда». На рабочий лист MS
Excel вводятся
исходные данные, после чего строится
точечная диаграмма, представляющая
собой поле
корреляции (диаграмму
рассеивания). Если щелкнуть правой
кнопкой мыши на любой точке данных и в
контекстном меню выбрать команду
«Добавить линию тренда…», то появится
диалоговое окно. В диалоговом окне на
вкладке «Тип» необходимо щелкнуть по
пиктограмме, например, «Линейная».
Далее необходимо
открыть вкладку «Параметры» и в области
«Название аппроксимирующей (сглаженной)
кривой» выбрать опцию «автоматическое:».
Следует убедиться, что опция «пересечение
кривой с осью Y в точке:» не отмечена.
Далее следует включить опции «показывать
уравнение на диаграмме» и «поместить
на диаграмму величину достоверности
аппроксимации (R^2)»
и щелкнуть на кнопке ОК. После этого
необходимо выделить текст с уравнением
регрессии и значением R2
и перетащить на свободное место диаграммы.
Построить линейное
уравнение регрессии и выполнить расчет
его характеристик можно с помощью режима
Регрессия
модуля Анализ
данных
надстройки «Пакет
анализа» процессора MS
Excel
следующим образом:
1) проверить доступ
к пакету анализа. В главном меню выбирается
Сервис/Надстройки
и устанавливается флажок Пакет
анализа;
2) в главном меню
выбрать Сервис/Анализ
данных/Регрессия;
3) заполнить
диалоговое окно ввода данных и параметров
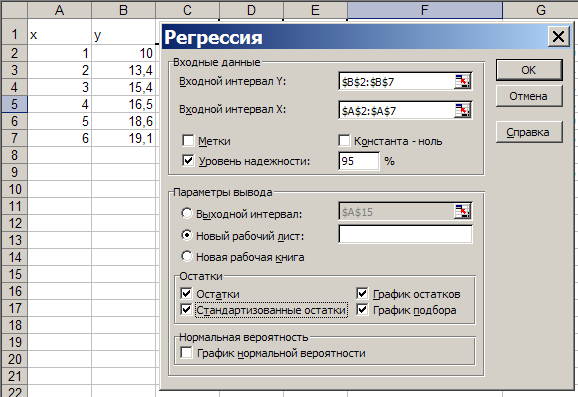
вывода (рисунок 1.2).
В
диалоговом окне режима Регрессия
(см. рисунок 1.2) задаются следующие
параметры.
Входные данные:
– Входной интервал
Y
– вводится
диапазон адресов ячеек, содержащих
значения уi
(ячейки
должны составлять один столбец);
– Входной интервал
X
– вводится диапазон адресов ячеек,
содержащих значения независимых
переменных. Значения каждой переменной
представляются одним столбцом. Количество
переменных – не более 16;
– Метки
– флажок включается, если первая строка
во входном диапазоне содержит заголовок.
В этом случае автоматически будут
созданы стандартные названия;
– константа-ноль
– при
включении этого параметра коэффициент
а =
0;
– уровень
надежности. Данный
флажок устанавливается в активное
состояние, если в поле, расположенное
напротив флажка, необходимо ввести
уровень надежности, отличный от уровня
95 %, применяемого по умолчанию. Принятый
уровень надежности используется для
проверки значимости коэффициента
детерминации R2
и
коэффициентов регрессии
.
Параметры
вывода:
– Выходной
интервал – при
включении активизируется поле, в которое
необходимо ввести адрес левой верхней
ячейки выходного диапазона, который
содержит ячейки с результатами вычислений
режима Регрессия;
– Новый рабочий
лист – при
включении этого параметра открывается
новый лист, в который, начиная с ячейки
А1, вставляются результаты работы режима
Регрессия;
– Новая рабочая
книга – при
включении этого параметра открывается
новая книга, на первом листе которой,
начиная с ячейки А1, вставляются результаты
работы режима Регрессия.
остатки:
– остатки
– при
включении вычисляется столбец, содержащий
невязки
,
;
– стандартизованные
остатки – при
включении вычисляется столбец, содержащий
стандартизованные остатки;
– график
остатков –
при включении выводятся точечные графики
невязки
,
в зависимости
от значений переменных
.
Количество графиков равно числуm
переменных
.
Далее рассмотрены
показатели, объединенные названием
Регрессионная
статистика (см.
ВЫВОД ИТОГОВ к примеру расчета) (рисунок
1.3).
Множественный
R
– коэффициент
корреляции
.
R-квадрат
– коэффициент
детерминации R2.
Нормированный
R-квадрат
– приведенный
коэффициент детерминации R2.
Стандартная
ошибка – оценка
s
для
среднеквадратического отклонения.
Наблюдения –
число
наблюдений п.
Далее рассмотрены
показатели,
объединенные названием Дисперсионный
анализ
(см.
ВЫВОД
ИТОГОВ к примеру расчета) (см. рисунок 1.3).
Столбец df
– это число
степеней свободы, которое для строкиРегрессия
определяется
числом параметров при
переменных х
в уравнении
регрессии и равно т.
Для строки
Остаток число
степеней свободы определяется числом
наблюдений n
и количеством переменных в уравнении
регрессии т + 1:
.
Для строкиИтого
число степеней
свободы определяется суммой чисел
и
.
Столбец SS
– сумма
квадратов отклонений. Для строки
Регрессия –
это сумма квадратов отклонений
теоретических данных от среднего. Для
строки Остаток
– это сумма
квадратов отклонений экспериментальных
данных от теоретических.
Для строки
Итого –
это сумма квадратов отклонений
экспериментальных данных от среднего.
Столбец MS
– дисперсии.
Для строки Регрессия
– факторная
дисперсия, для строки Остаток
– остаточная
дисперсия.
Столбец F –
расчетное значение F-критерия
Фишера
.
Столбец
Значимость
F
– значение
уровня значимости, соответствующее
вычисленному значению
.
Определяется
с помощью функции = FРАСП(Fp;
df(регрессия);
df(остаток)).
Если
значимость
F
меньше уровня значимости α (обычно α =
0,05), то построенная регрессия является
значимой.
Столбец Коэффициенты
– значения
коэффициентов a,
b.
Столбец Стандартная
ошибка – значения
.
t-статистика
– расчетные
значения t-критерия.
Р-значение
– значения
уровней значимости, соответствующие
вычисленным значениям tр.
Определяются с помощью функции =
СТЬЮДРАСП(tр;
n–m–1).
Если
Р-значение
меньше уровня значимости α,
то
принимается гипотеза о значимости
соответствующего коэффициента регрессии.
Нижние 95 % и
Верхние 95 %
– соответственно
нижние и верхние границы доверительных
интервалов для коэффициентов регрессии.
Далее рассмотрены
показатели, объединенные названием
Вывод
остатка
(см. ВЫВОД
ИТОГОВ к примеру расчета) (см. рисунок
1.3).
Столбец «Наблюдение»
содержит номера наблюдений.
Столбец «Предсказанное
y»
содержит значения
,
вычисленные по построенному уравнению
регрессии.
Столбец «Остатки»
содержит значения невязок
,
которые вычисляются как разность между
эмпирическимиу
и теоретическими
значениями результативного признакаy.
Пример –
Зависимость
доли расходов
у на товары
длительного пользования в общих расходах
семьи в процентах от среднемесячных
доходов х
семьи (млн р.)
представлена полем
корреляций
на рисунке 1.1, а [5, с. 85]. Построить
уравнения линейной и логарифмической
регрессий и выбрать регрессию, наилучшим
образом описывающую исходные данные.
На основе рисунка
1.1, а можно выдвинуть гипотезу о том, что
наилучшим образом описывать исходные
данные будет, скорее всего, логарифмическая
функция. Проверим это утверждение.
С помощью команды
«Добавить линию тренда» на
рисунке 1.1, б
построены линии линейного и логарифмического
трендов.
Параметры полученных уравнений регрессий
представлены в таблице 1.2.
По формулам,
представленным в таблице 1.1, рассчитаны
основные характеристики построенных
регрессий. Результаты расчетов
представлены таблицами 1.3 и 1.4.
Результаты
построения линейного уравнения регрессии
и расчета его характеристик с помощью
режима Регрессия
модуля Анализ
данных
надстройки «Пакет анализа» представлены
на рисунках 1.3 и 1.4.
Сравнение
результатов, полученных с помощью
расчетных формул, с результатами
применения инструментальных средств
Excel
показывает их близость, что свидетельствует
о правильном понимании методики
построения линейных регрессионных
уравнений и оценки их качества.
а) б)
а – пары чисел
,
которые представляют собой поле
корреляции; б – графики линейной (1) и
логарифмической (2) регрессий
Рисунок 1.1 – Графики поля корреляций,
линейной и логарифмической регрессий
Таблица 1.2 – Уравнения линейной и
логарифмической регрессий
|
Функция |
линейная |
логарифмическая |
|
a |
9,28 |
9,8759 |
|
b |
1,7771 |
5,1289 |
|
Уравнение |
|
|
Далее необходимо
выбрать регрессию, наилучшим образом
описывающую исходные данные.
Из расчетов видно,
что наименьшая остаточная дисперсия –
в логарифмической функции (0,0811).
Индекс корреляции
= 0,9916превышает значение
линейного коэффициента корреляции
= 0,9742.
При этом 97%
вариации результативного признака y
логарифмической регрессии объясняется
вариацией фактора х,
а 3 % приходится на долю прочих факторов.
Наименьшая средняя
ошибка аппроксимации ,
задающая среднее отклонение расчетных
значений от фактических, содержится в
логарифмической регрессии:
=1,3
(что не выходит за пределы интервала в
8–10 %).
Таким образом,
наилучшим образом описывать исходные
данные будет логарифмическая регрессия,
что подтверждается значениями
,
,
.

1.3 – Исходные данные к расчетам
|
Номер наблюдения |
х |
y |
|
xy |
|
линейная |
|
|
логарифми-ческая |
|
|
|
1 |
1 |
10 |
1 |
10 |
100 |
11,0571 |
1,1175 |
10,5710 |
9,8759 |
0,0154 |
1,2410 |
|
2 |
2 |
13,4 |
4 |
26,8 |
179,56 |
12,8342 |
0,3201 |
4,2224 |
13,4310 |
0,0010 |
0,2312 |
|
3 |
3 |
15,4 |
9 |
46,2 |
237,16 |
14,6113 |
0,6220 |
5,1214 |
15,5106 |
0,0122 |
0,7180 |
|
4 |
4 |
16,5 |
16 |
66 |
272,25 |
16,3884 |
0,0125 |
0,6764 |
16,9861 |
0,2363 |
2,9458 |
|
5 |
5 |
18,6 |
25 |
93 |
345,96 |
18,1655 |
0,1888 |
2,3360 |
18,1305 |
0,2204 |
2,5239 |
|
6 |
6 |
19,1 |
36 |
114,6 |
364,81 |
19,9426 |
0,7100 |
4,4115 |
19,0657 |
0,0012 |
0,1798 |
|
Среднее |
3,5 |
15,5 |
15,1667 |
59,4333 |
249,9567 |
– |
– |
4,5565 |
– |
– |
1,3066 |
Т
1.4 – Результаты расчетов
|
Функция |
линейная |
логарифмическая |
|
|
Среднеквадратическая |
|
||
|
Среднеквадратическая |
|
||
|
Линейный корреляции |
|
– |
|
|
Индекс корреляции |
– |
|
|
|
Коэффициент |
|
– |
|
|
Индекс детерминации |
– |
|
|
|
Табличное значение |
|
||
|
|
|||
|
Функция |
линейная |
логарифмическая |
|
|
Расчетное значение |
|
|
|
|
Средняя ошибка |
|
|
|
|
Коэффициент |
|
|
|
|
Общая дисперсия |
|
||
|
Остаточная признака у |
|
|
|
|
Стандартная коэффициента а |
|
|
|
|
Стандартная коэффициента b |
|
|
|
|
Расчетные
|
a |
|
|
|
b |
|
|
|
|
Табличное Стьюдента |
|
Рисунок 1.2 – Диалоговое окно режима
Регрессия
Рисунок 1.3 – Вывод итогов к расчету

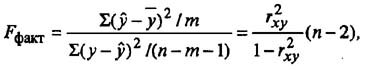
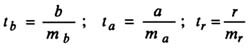
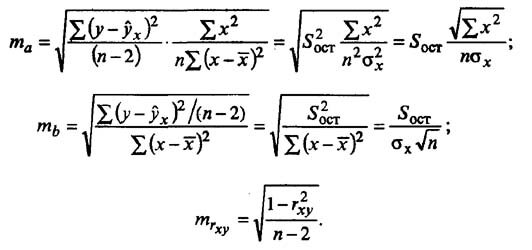
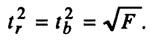

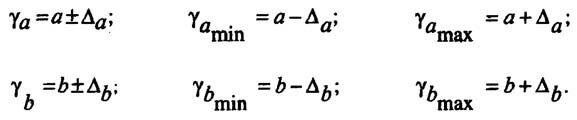
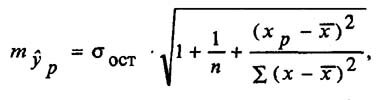
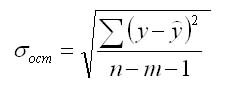
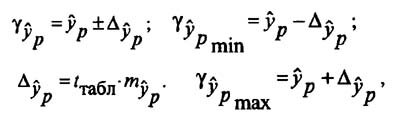
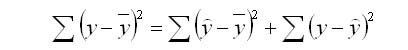
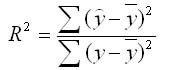
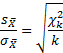
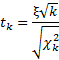






 Окончание таблицы 1.4
Окончание таблицы 1.4 

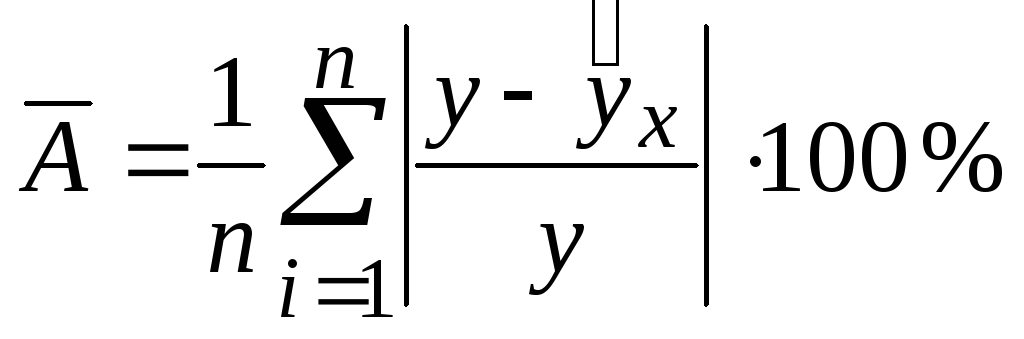 =4,5565
=4,5565 =0,0811
=0,0811