Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ — время движения тела.
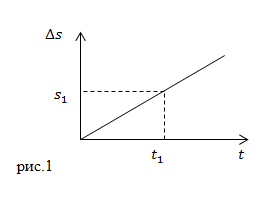
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
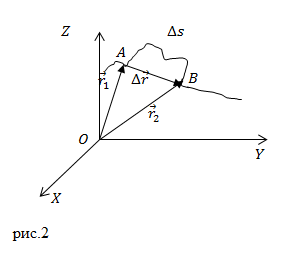
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($Delta overline{r}$).
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ — единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
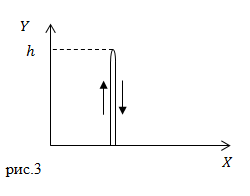
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
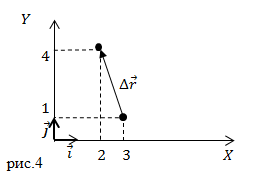
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
Радиус — вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус — вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
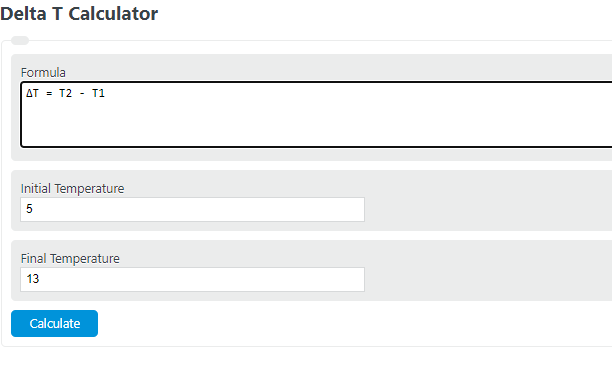
Enter the initial temperature and final temperature of a substance or object to calculate the delta T.
- Mixed Air Temperature Calculator
- Change in Internal Energy Calculator
- Thermal Energy Calculator
Delta T Formula
The following formula is used to calculate delta T.
- Where ΔT is the change in temperature (delta T)
- T2 is the final temperature
- T1 is the initial temperature
To calculate delta T, simply subtract the initial temperature from the final temperature.
Delta T Definition
Delta T, denoted ΔT, is the term and symbol used to describe the change in temperature of a substance, system, or object. the delta in delta T is the term used to describe the change in and the T denotes temperature.
Delta T Example
How to calculate delta T?
- First, determine the initial temperature.
Measure the initial temperature of the material.
- Next, determine the final temperature.
Measure the final temperature of the material over the time period.
- Finally, calculate the delta T.
Calculate the change in temperature by subtracting the initial temperature from the final temperature.
FAQ
What is delta?
Delta is a symbol used in mathematics and science to describe the change in a value. For example ΔT is the change in temperature while ΔP is the change in pressure and so forth.

Привет! Найти это всё очень просто, зная просто-напросто формулы.
Чтоб найти конечную температуру или t2 в физике, надо следовать вот этой формуле: t1+дельта t. Как видишь, всё просто.
t1 — это начальная температура, а дельта t — это изменение температуры.
Чтоб найти t1, надо сделать так: из t2 вычесть дельта t.
А чтобы найти дельту t, надо Q разделить на cm.
Чтобы найти массу, зная лишь объем, надо этот самый известный объем просто умножить на плотность вещества. Плотность можно найти в таблице плотностей, она есть в учебниках, на физике она часто встречается и её разрешают пользоваться.
—
Самое главное, — записывай всё, что диктует тебе учитель. Это важно! Зная формулы, легко решишь то, что тебе надо. Физику понимать надо, её не заучишь как тот же русский язык.
Формула для расчета количества теплоты
Допустим, на нужно узнать, какое количество теплоты получила при нагревании железная деталь. Масса детали $3 space кг$. Деталь нагрелась от $20 degree C$ до $300 degree C$.
Возьмем значение теплоемкости железа из таблицы — $460 frac{Дж}{кг cdot degree C}$. Объясним смысл этой величины: на нагревание куска железа массой $1 space кг$ на $1 degree C$ необходимо затратить количество теплоты, равное $460 space Дж$.
- Масса детали у нас в 3 раза больше, значит, на ее нагрев потребуется в 3 раза большее количество теплоты — $1380 space Дж$
- Температура изменилась не на $1 degree C$, а на $280 degree C$
- Значит, необходимо в 280 раз большее количество теплоты: $1380 space Дж cdot 280 = 386 400 space Дж$
Тогда, формула для расчета количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении примет вид:
$Q = cm(t_2 — t_1)$,
где $Q$ — количество теплоты, $c$ — удельная теплоемкость вещества, из которого состоит тело, $m$ — масса тела, $t_1$ — начальная температура тела, $t_2$ — конечная температура тела.
Чтобы рассчитать количество теплоты, которое необходимо затратить для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость умножить на массу тела и на разность конечной и начальной температур.
Рассмотрим подробнее особенности расчета количества теплоты на примерах решения задач.
Видео
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела, $c_{mu}=c cdot mu$ — молярная теплоемкость, $mu$ – молярная масса вещества, $nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты ($Delta Q$), которое получает тело при увеличении его температуры на величину $Delta t = t_2 — t_1$ можно вычислить как:
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности ($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Определить вещество, лежащее в основе тела, если при нагревании его с 200 до 600К ему передалось 4,*106Дж. Масса тела 40 кг.
Решение
Чтобы решить задачу, необходимо узнать удельную теплоемкость этого вещества, затем — по таблице узнать его название.
C=Q÷mΔT
C=4,*106÷40*400=,25*103Дж/кгК
По таблице находим, что такую удельную теплоемкость имеет олово.
Масса воды в сосуде 800г, температура 60оС. В эту воду помещают лед с температурой -10оС. Какой массы лед был помещен, если термодинамическое равновесие установилось, когда температура воды стала равной 40оС.
Решение
Из таблиц определяем, что удельная теплоемкость воды равна 4,2*103Дж/кгК, льда -2,1*103Дж/кгК. λ льда (удельная теплота плавления) =3,33*105Дж/кг.
Для состояния теплового баланса характерно:
с2m2(to-t2)+λm2+c1m2(t3-to)+c1m1(t3-t1)=
Находим m2:
m2=c1m1(t1-t3)⁄(c2(to-t2)+λ+c1(t3-t))
Подставляя значения, находим величину массы, равную 0,13 кг.
Определить Q, выделившееся при охлаждении 20 л масла, если его температура снизилась с 60оС до 20оС.
Первым делом, для перехода в систему СИ заменяем объем, выраженный в литрах, на единицу м3:20л=,02м3.
Q=cmΔT.
В то же время m=ρV/
Найдя в таблице ρ, высчитываем массу масла: m=90*,02=18кг
Разница температур составила 40оС.
Q=1800*18*40=1296(кДж).
Теги
0 рейтинг
Как найти дельта t зная t1 и t2
- найти
- дельта
- 5 — 9 классы
- физика
Gilfanovar01_zn
в разделе Физика
Всего ответов: 2
0 рейтинг
Приставка дельта означает разницу
t2-t1
Ruslan0177_zn
Начинающий
0 рейтинг
Просто вычисли по такой формуле: t1-t2=▲t
112233445566778811_zn
Начинающий