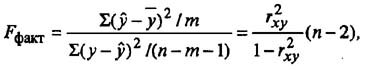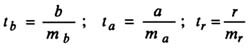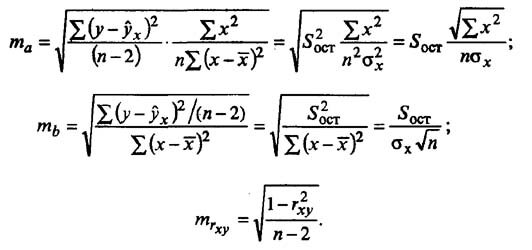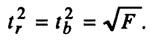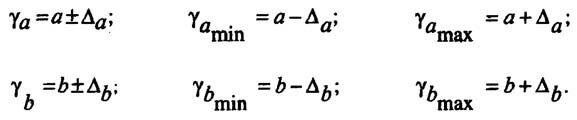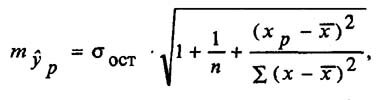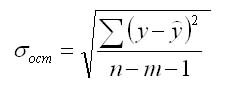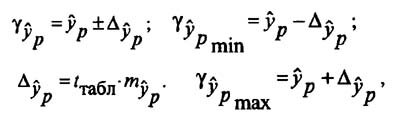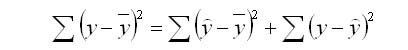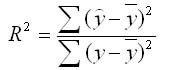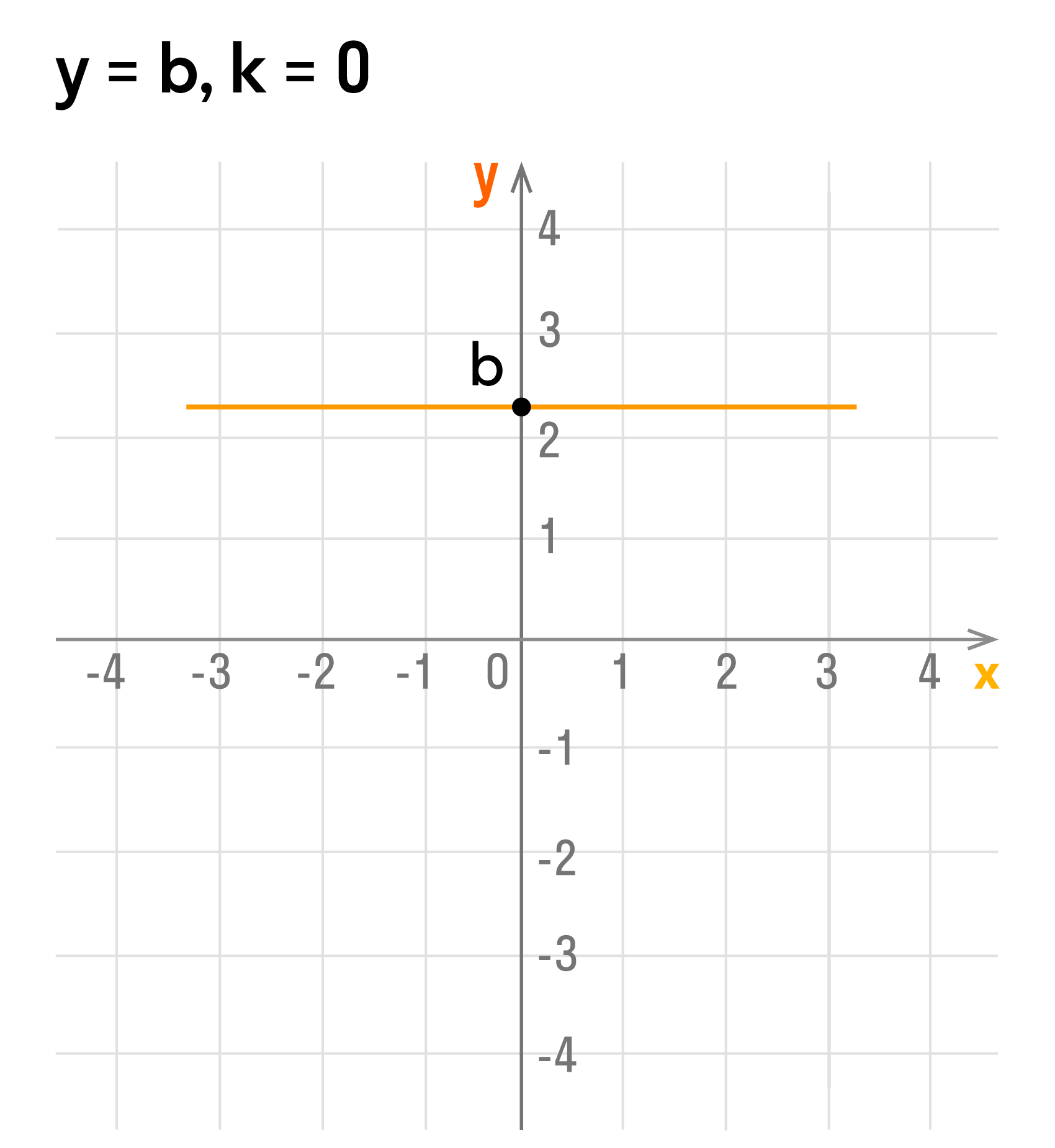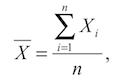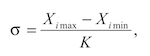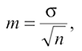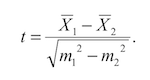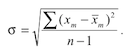Критерий Фишера и Стьюдента
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
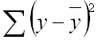
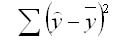
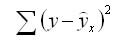
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Любые задачи по эконометрике решаются здесь
Как считать коэффициент Стьюдента в Excel?
Расчет критерия Стьюдента в Excell
- Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)
- Ставим курсор в пустую ячейку
- На панеле инструментов нажимаем кнопку fx (вставить формулу)
- В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень
Что значит коэффициент Стьюдента?
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Что такое табличный коэффициент?
табличный коэффициент. , который соответствует числу измерений в группе, — подставить полученные значения в формулу и произвести необходимые вычисления. — общее число индивидуальных результатов соответственно в экспериментальной и контрольной группах.
Как вычислить число степеней свободы для t критерия Стьюдента?
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t—критерия Стьюдента. Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t—критерия Стьюдента для связных и, очевидно, равных по численности выборок.
Как использовать критерий Стьюдента?
Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.
Как рассчитать критерий Вилкоксона?
Расчет T-критерия Вилкоксона заключается в выполнении следующих шагов:
- Составить список значений испытуемых в первом и во втором замерах.
- Найти разность по каждому замеру, т. …
- Найти значения разностей по модулю.
- Ранжировать полученные на 4-ом шаге значения, по принципу меньшему значения приписывается меньший ранг.
Что показывает т тест?
Критерий Стьюдента (t—тест) — это статистический метод, который позволяет сравнивать средние значения двух выборок и на основе результатов теста делать заключение о том, различаются ли они друг от друга статистически или нет.
Как активировать функцию Ттест?
Чтобы применить функцию ТТЕСТ,
- щелкните по значку Вставить функцию , расположенному на верхней панели инструментов, …
- выберите из списка группу функций Статистические,
- щелкните по функции ТТЕСТ,
- введите требуемые аргументы через точку с запятой или выделите мышью диапазон ячеек,
- нажмите клавишу Enter.
Для чего используется t статистика Стьюдента?
t-критерий Стьюдента для независимых выборок применяется для сравнения средних значений двух независимых между собой выборок. Условия применения: Сравниваемые значения не составляют пару коррелирующих значений Распределение признаков в каждой выборке соответствует нормальному распределению
Что такое число хвостов распределения?
хвосты – число, определяющее, будет ли вычисляемое распределение односторонним или двусторонним (1, если хвост один, и 2, если хвоста два).
Чем отличается критерий Стьюдента от Манна Уитни?
U-критерий Манна—Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей. U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака.
Как оценить погрешность?
Относительная погрешность измерения – это погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%.
Как оценить ошибку измерений?
Для наглядной оценки точности измерения удобно также использовать относительную величину погрешности: εx=δxxизм. Она показывает, насколько погрешность мала по сравнению с самой измеряемой величиной (её также можно выразить в процентах: ε=δxx⋅100%).
В каком критерии используется распределение Стьюдента?
Распределение Стьюдента играет важную роль в статистическом анализе и используется, например, в t-критерии Стьюдента для оценки статистической значимости разности двух выборочных средних, при построении доверительного интервала для математического ожидания нормальной совокупности при неизвестной дисперсии, а также в …
Как вычислить погрешность косвенного измерения?
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм. При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует выражать в одних и тех же единицах! Задание 1.
Как определить достоверность различий?
Основными способами проверки достоверности информации являются:
- сопоставление с рыночными данными (как из сегмента, к которому принадлежит объект оценки, так и с общерыночными закономерностями);
- сопоставление с аналогичными данными из иного источника;
- проверка отсутствия противоречия между частями информации;
Что такое T в статистике?
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Линейная функция
Функция не всегда сразу задана в виде (y=kx+b), иногда такой вид получится только после преобразований. Например, (y=6(x-1)+10x) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим (y=16x-6).
График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
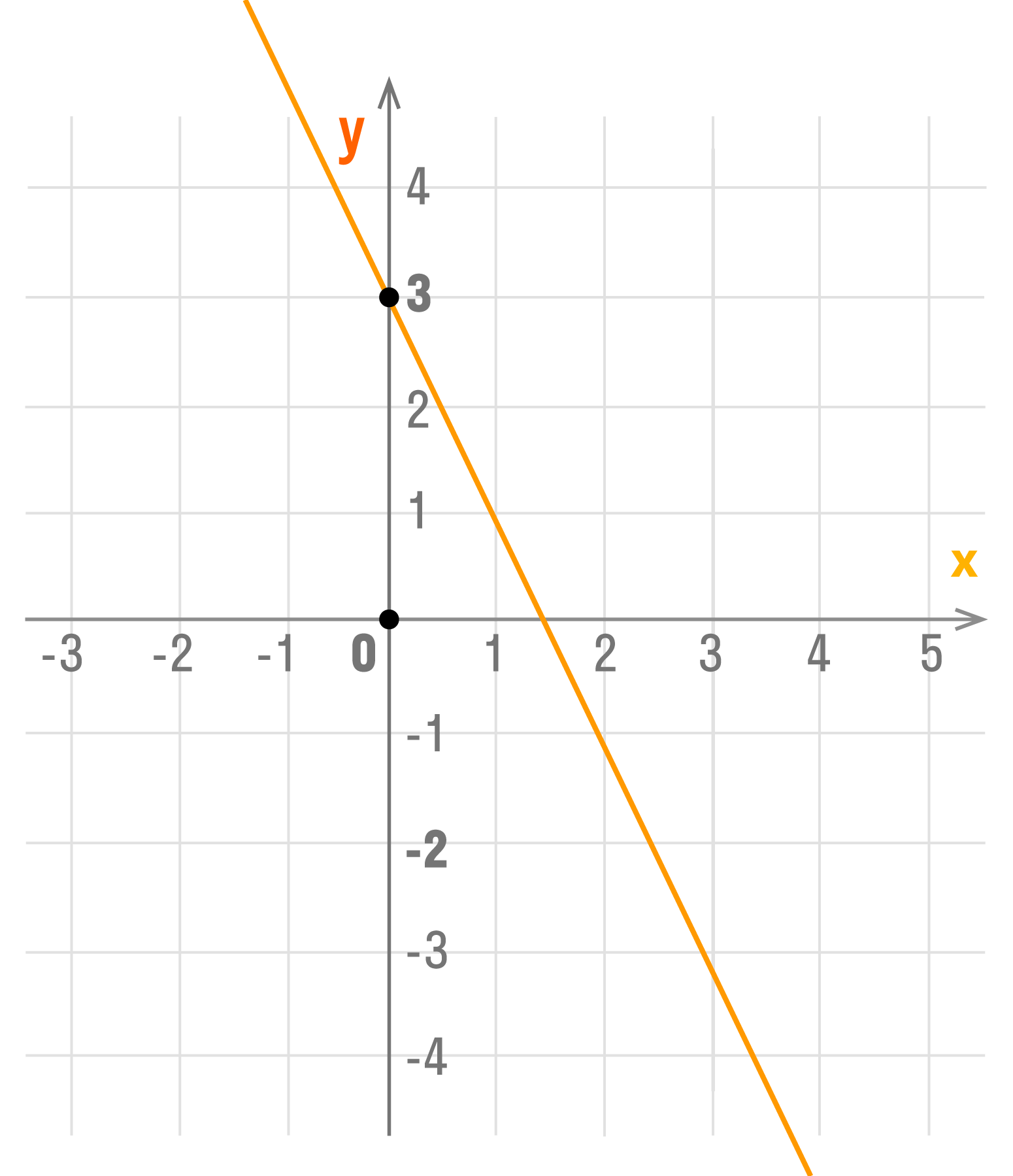
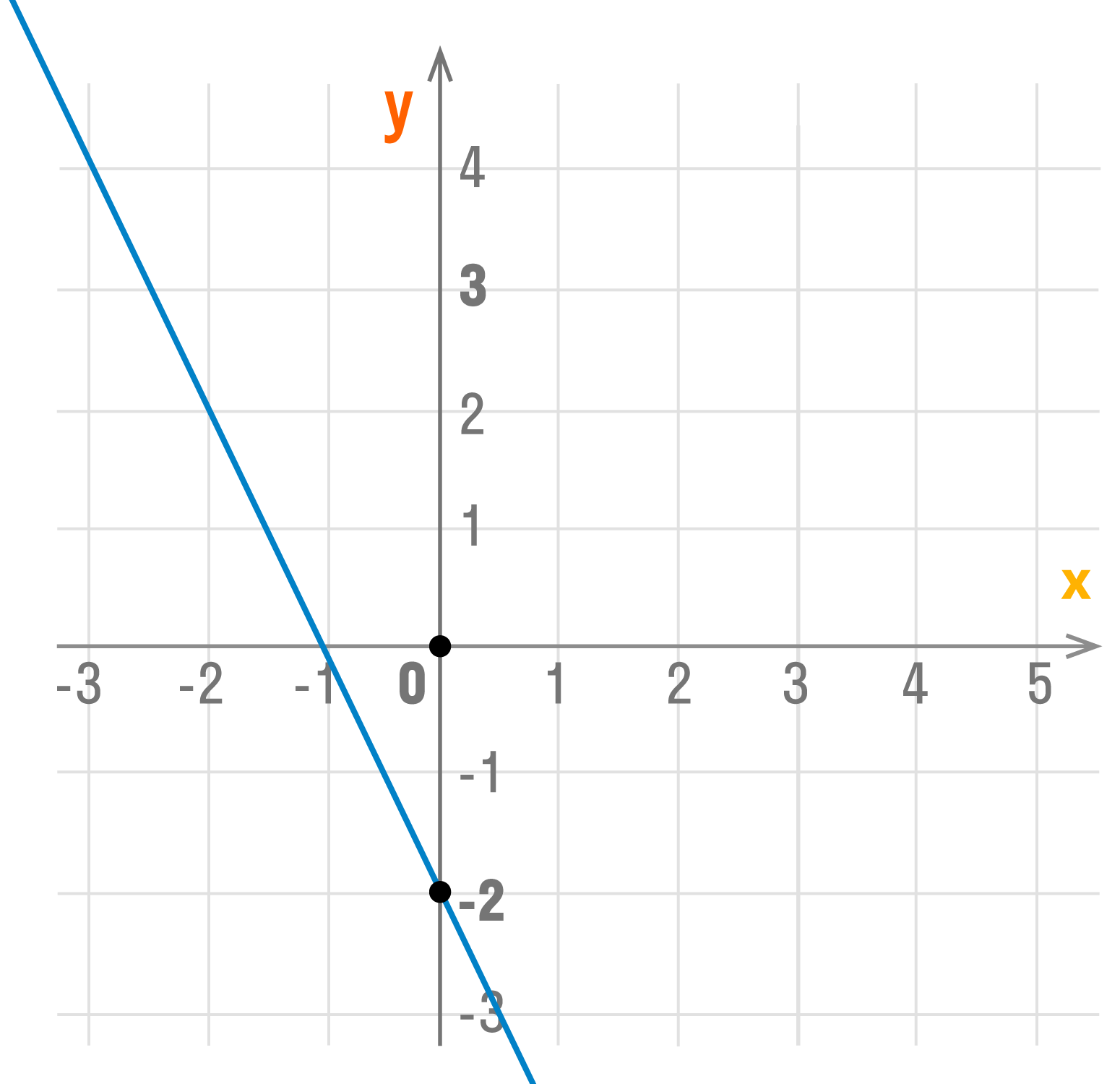
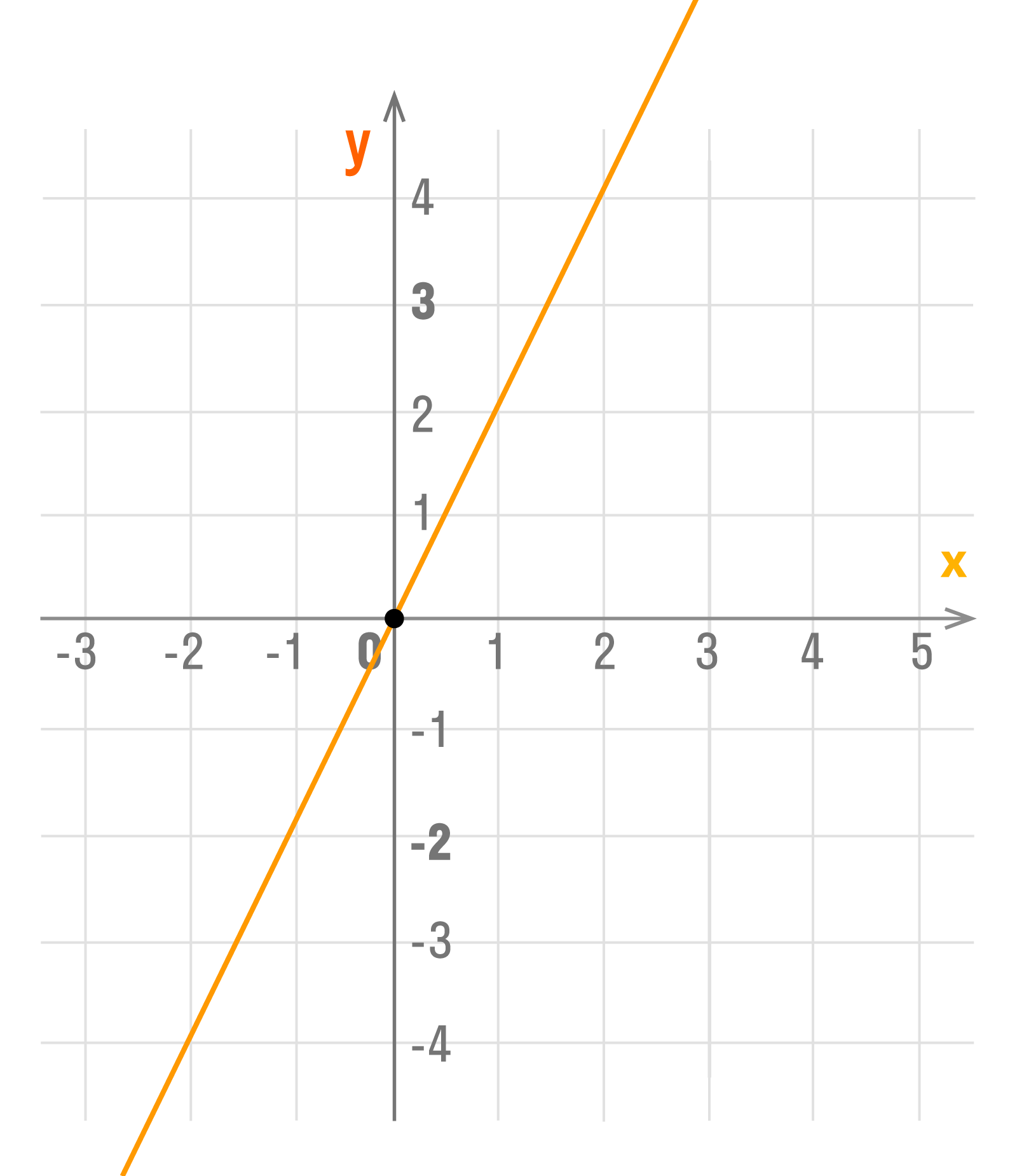
Чтобы в этом убедиться построим графики функций (y=2x), (y=fracx-5), (y=8).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Как меняется график при разных (k)?
Чтобы определить, как влияет на график коэффициент (k), построим несколько функций разными (k): (frac),(-frac),(2),(-2) и (0). При этом во всех функциях сделаем (b) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: (y=fracx), (y=-fracx), (y=2x), (y=-2x), (y=0).
Заметьте, что при (k=2) и (frac) — функция возрастает, а при (k=-2) и (-frac) — убывает. На самом деле:
При любом (k>0) функция возрастает и при любом (k<0) — убывает. Когда же (k=0) — она не возрастает и не убывает, а идет параллельна оси (x) (или совпадает с ней).
Так же можно заметить, чем больше модуль (k), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента (k) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение (k) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях (|k|=frac). То есть на первом графике (k=2),а на втором (k=-frac).
Как меняется график при разных значениях (b)?
Чтобы определить, как (b) влияет на график, построим несколько функций с разными (b): (6), (2), (0), (-3) и (-8). При этом (k) пусть во всех функциях будет равен (2).
Не сложно заметить, что прямая либо поднимается на (b) (если (b>0)) либо опускается на (|b|) если
((b<0)).
Как по графику функции определить значение (b)?
Очень просто — прямая пересекает ось (y) всегда в точке (b). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида (y=kx+b). Установите соответствие между графиками функций и знаками коэффициентов (k) и (b).
A. 

Коэффициенты
| 1) (k>0),(b>0) | 2) (k<0), (b>0) | 3) (k<0), (b<0) | 4) (k>0), (b<0) |
Решение:
А. – функция убывает, поэтому (k<0). Точка пересечения оси (y) и прямой находится выше нуля, значит (b>0). Подходит вариант под цифрой 2).
B. — функция возрастает — (k>0). Точка пересечения оси (y) и прямой находится выше нуля, значит (b>0). Подходит вариант под цифрой 1).
C. – функция убывает — (k<0). Точка пересечения оси (y) и прямой находится ниже нуля, значит (b<0). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Отмечаем точку (b) на оси игреков.
От неё идем вправо на количество клеточек равное знаменателю (k), и вверх на количество клеточек равное числителю (k) (если (k>0)) или вниз на тоже количество (если (k<0)).
Проводим через эти две точки прямую.
Пример: Построить график функции (y=3x+1).
(b=1), поэтому отмечаем точку с этим значением на оси (y)
(k=3), а тройка это тоже самое, что (frac). При этом (k>0). Поэтому идем вправо на единицу и вверх на (3). Ставим точку.
Проводим через эти две точки прямую.
Пример: Построить график функции (y=-frac x-3).
(b=-3) отмечаем точку с этим значением на оси (y).
(k=-frac), (k<0), числитель (1), знаменатель (4). Значит, идем вправо на (4) и вниз на единицу.
Проводим через эти две точки прямую.
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
График линейной функции, его свойства и формулы
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
Понятие линейной функции
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
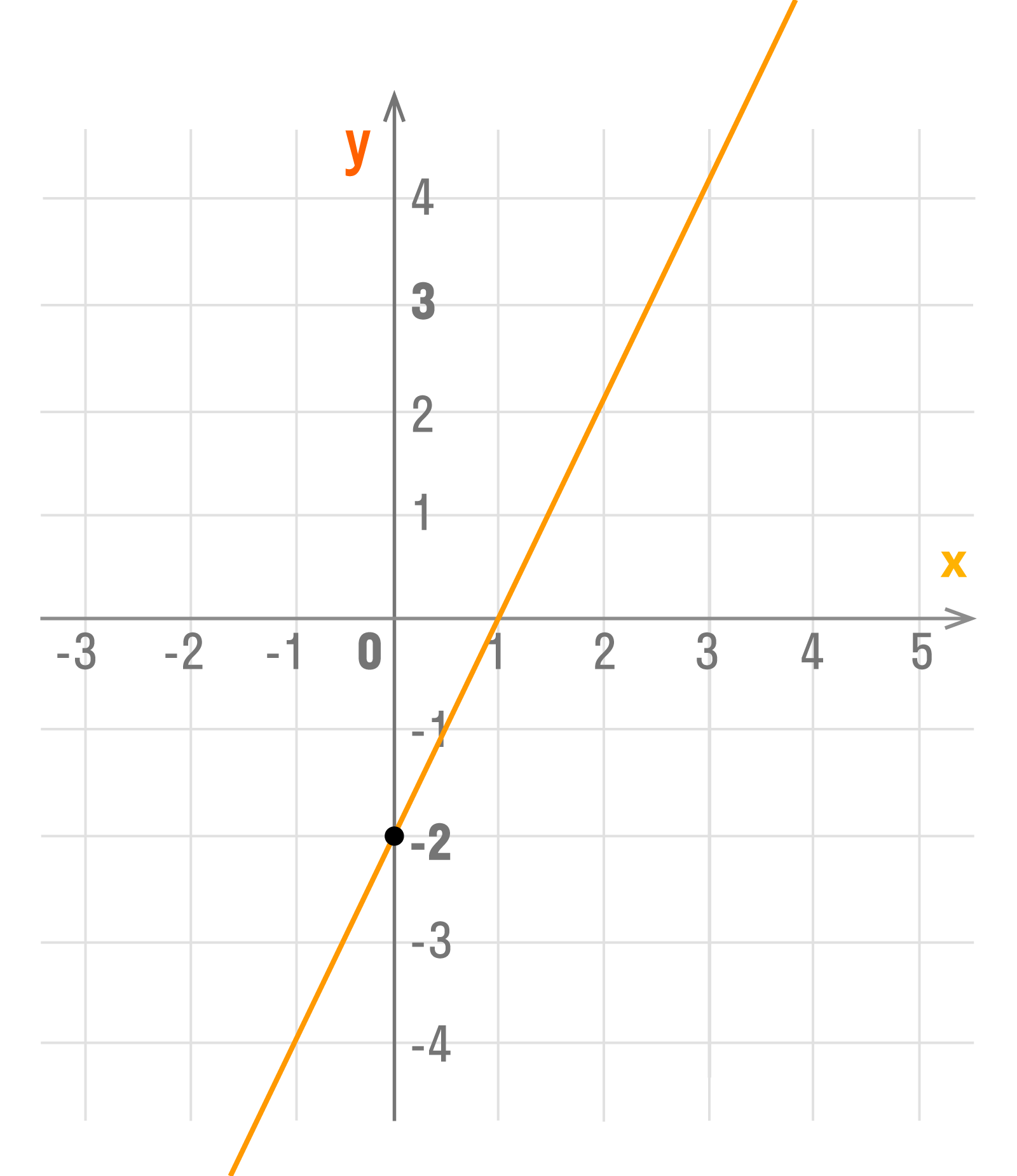
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k < 0.
При k > 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k < 0 функция принимает отрицательные значения на промежутке (−b/k; +∞) и положительные значения на промежутке (−∞; −b/k).
Коэффициент k характеризует угол, который образует прямая с положительным направлением OX. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k < 0 — тупой, если k = 0, то прямая совпадает с осью OX.
Есть два частных случая линейной функции:
Если b = 0, то уравнение примет вид y = kx. Такая функция называется прямой пропорциональностью. График — прямая, которая проходит через начало координат.
- Если k = 0, то уравнение примет вид y = b. График — прямая, которая параллельна оси OX и проходит через точку (0; b).
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k < 0, то график наклонен влево.
Коэффициент b отвечает за сдвиг графика вдоль оси OY:
если b > 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b < 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вниз вдоль оси OY.
Начертим три графика функции:
y = 2x + 3;
y = 1/2x + 3;
y = x + 3.
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
Теперь рассмотрим графики функций:
y = −2x + 3;
y = −1/2x + 3;
y = −x + 3.
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Рассмотрим графики функций:
y = 2x + 3;
y = 2x;
y = 2x − 2.
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k < 0 и b > 0, то график функции y = kx + b выглядит так:
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
Если k > 0 и b < 0, то график функции y = kx + b выглядит так:
Если k < 0 и b < 0, то график функции y = kx + b выглядит так:
Если k = 0, то функция y = kx + b преобразуется в функцию y = b. В этом случае ординаты всех точек графика функции равны b. А график выглядит так:
Если b = 0, то график функции y = kx проходит через начало координат. Так выглядит график прямой пропорциональности:
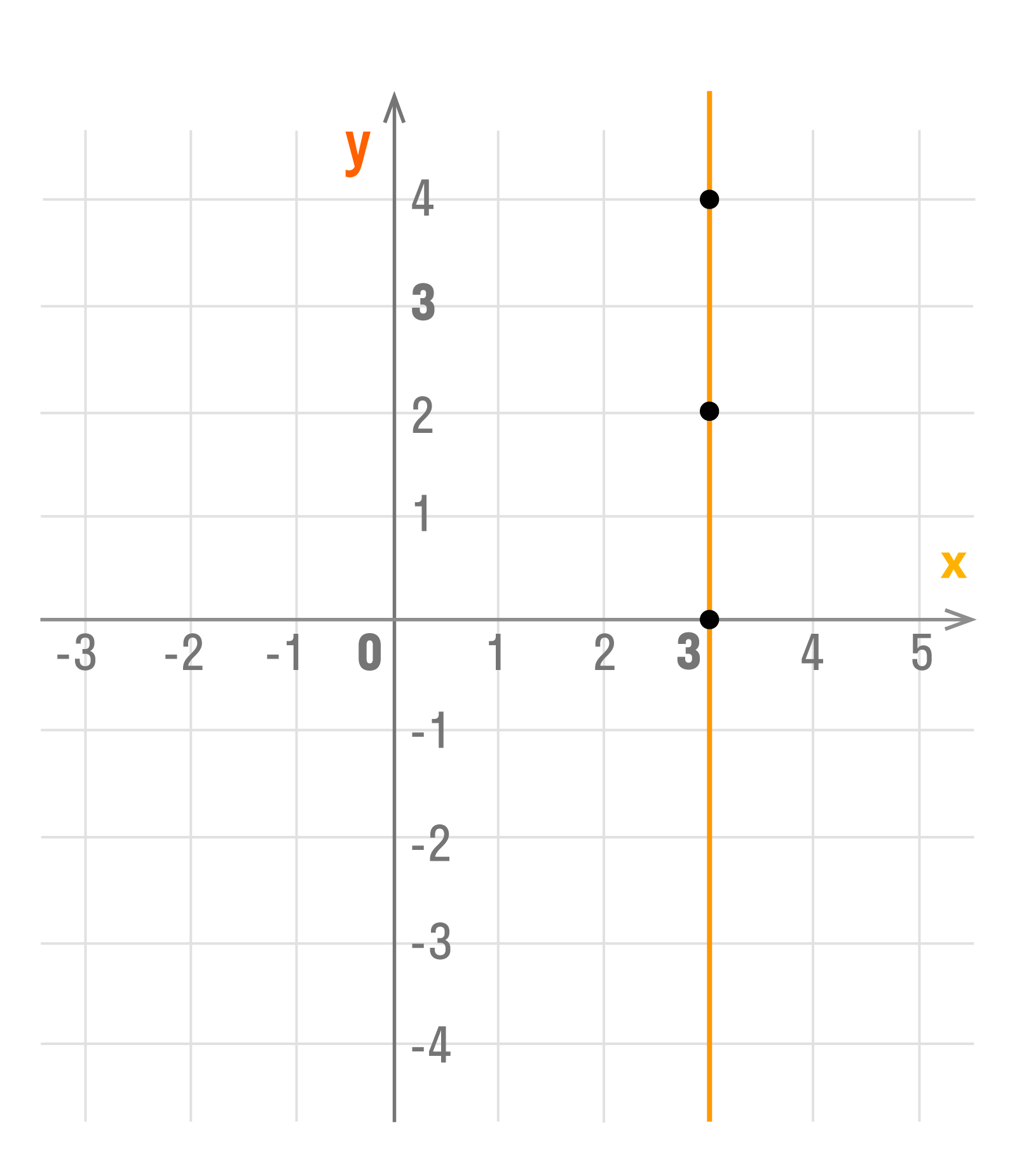
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Числовой коэффициент выражения: определение, примеры
В математических описаниях часто фигурирует термин «числовой коэффициент», например, в работе с буквенными выражениями и выражениями с переменными. Материал статьи ниже раскрывает понятие этого термина, в том числе, на примере решения задач на нахождение числового коэффициента.
Определение числового коэффициента. Примеры
Учебник Н.Я. Виленкина (учебный материал для учащихся 6 классов) задает такое определение числового коэффициента выражения:
Если буквенное выражение является произведением одной или нескольких букв и одного числа, то это число называется числовым коэффициентом выражения.
Числовой коэффициент зачастую называют просто коэффициентом.
Данное определение дает возможность указать примеры числовых коэффициентов выражений.
Рассмотрим произведение числа 5 и буквы a , которое будет иметь следующий вид: 5 · a . Число 5 является числовым коэффициентом выражения согласно определению выше.
В заданном произведении x · y · 1 , 3 · x · x · z десятичная дробь 1 , 3 – единственным числовой множитель, который и будет служить числовым коэффициентом выражения.
Также разберем такое выражение:
7 · x + y . Число 7 в данном случае не служит числовым коэффициентом выражения, поскольку заданное выражение не является произведением. Но при этом число 7 – числовой коэффициент первого слагаемого в заданном выражении.
Пусть дано произведение 2 · a · 6 · b · 9 · c .
Мы видим, что запись выражения содержит три числа, и, чтобы найти числовой коэффициент исходного выражения, его следует переписать в виде выражения с единственным числовым множителем. Собственно, это и является процессом нахождения числового коэффициента.
Отметим, что произведения одинаковых букв могут быть представлены как степени с натуральным показателем, поэтому определение числового коэффициента верно и для выражений со степенями.
Выражение 3 · x 3 · y · z 2 – по сути оптимизированная версия выражения 3 · x · x · x · y · z · z , где коэффициент выражения – число 3 .
Отдельно поговорим о числовых коэффициентах 1 и — 1 . Они очень редко записаны в явном виде, и в этом их особенность. Когда произведение состоит из нескольких букв (без явного числового множителя), и перед ним обозначен знак плюс или вовсе нет никакого знака, мы можем говорить, что числовым коэффициентом такого выражения является число 1 . Когда перед произведением букв обозначен знак минус, можно утверждать, что в этом случае числовой коэффициент – число — 1 .
Далее определение числового коэффициента расширяется с произведения нескольких букв и числа до произведения числа и нескольких буквенных выражений.
К примеру, в произведении — 5 · x + 1 число — 5 будет служить числовым коэффициентом.
По аналогии, в выражении 8 · 1 + 1 x · x число 8 – коэффициент выражения; а в выражении π + 1 4 · sin x + π 6 · cos — π 3 + 2 · x числовой коэффициент — π + 1 4 .
Нахождение числового коэффициента выражения
Выше мы говорили о том, что если выражение представляет собой произведение с единственным числовым множителем, то этот множитель и будет являться числовым коэффициентом выражения. В случае, когда выражение записано в ином виде, предстоит совершить ряд тождественных преобразований, который приведет заданное выражение к виду произведения с единственным числовым множителем.
Задано выражение − 3 · x · ( − 6 ) . Необходимо определить его числовой коэффициент.
Решение
Осуществим тождественное преобразование, а именно произведем группировку множителей, являющихся числами, и перемножим их. Тогда получим: − 3 · x · ( − 6 ) = ( ( − 3 ) · ( − 6 ) ) · x = 18 · x .
В полученном выражении мы видим явный числовой коэффициент, равный 18 .
Ответ: 18
Задано выражение a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 . Необходимо определить его числовой коэффициент.
Решение
С целью определения числового коэффициента преобразуем в многочлен заданное целое выражение. Раскроем скобки и приведем подобные слагаемые, получим:
a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 = = 2 · a 2 — 6 · a — a + 3 — 2 · a 2 + 6 · a — 3 = — a
Работа на результат
Диагностика и методы оценки
В практике физического воспитания существует множество методов и различных тестов, позволяющих объективно оценить состояние физического здоровья каждого школьника. При этом используются как медицинские, физиологические, психолого-педагогические, так и антропометрические подходы. Диагностика физического здоровья включает следующие показатели: антропометрические, физического развития, физической и функциональной подготовленности школьника. Годовая динамика изучаемых показателей является критерием эффективности физического воспитания, врачебно-педагогического контроля и самоконтроля.
Составной частью педагогического мониторинга в системе физического воспитания школьников является методика оценки физического развития и физической подготовленности учащихся, основу которой составляет тестирование. При этом тесты должны быть разносторонними и системными – это способствует поддержанию и повышению интереса учащихся к оценке собственного здоровья и слежению за динамикой его показателей.
Проблема тестирования физической подготовленности человека – одна из наиболее разработанных в теории и методике физического воспитания и спортивной метрологии проблем. Накоплен огромный и самый разнообразный материал, который всегда вызывал и продолжает вызывать к себе большой интерес со стороны не только научных работников, но и учителей физической культуры, тренеров, учащихся, их родителей.
Компьютерное тестирование физического состояния учащихся предполагает обязательное ознакомление учителя с элементарными методами математической статистики. Исходя из реальных возможностей и минимально необходимой объективной информации в условиях школы представляется целесообразным использование простейших методов оценки, не требующих сложной аппаратуры и длительных расчетов, а также больших затрат сил и времени. По результатам фактических измерений в соответствии с методикой исследования выполняется расчет индивидуальных показателей физического развития, физической подготовленности и функциональной подготовленности каждого учащегося, что поможет составить индивидуальную карту физического здоровья школьника.
Проверка делается на выборочной совокупности тестируемых с применением статистических методов обработки данных. Количество учащихся, подлежащих тестированию в каждом классе, зависит от его наполняемости. В окончательную обработку лучше включать данные только тех учащихся, которые прошли полную программу обследования. Чтобы получить однородный материал, иногда исключают самый лучший и самый худший результаты. На основании полученных данных рассчитываются основные статистические параметры отдельно для мальчиков и девочек по всем показателям.
В педагогических исследованиях для определения достоверности различий используется t-критерий Стьюдента, который относится к параметрическим критериям. Следовательно, его использование возможно только в том случае, когда результаты исследования представлены в виде измерений по шкале отношений.
Для осуществления таких измерений используются метрические системы оценок, примерами которых могут быть:
- измерения длины, высоты в принятых единицах, например роста учащихся, длины и высоты прыжков;
- измерения веса ученика или силы кисти;
- время выполнения упражнения: результаты в беге, плавании, лыжных гонках;
- число выполненных действий: количество подтягиваний, попаданий в цель и т.п.
Предположим, вам необходимо сравнить результаты тестирования учащихся параллельных классов или одного и того же класса в начале и конце учебного года. Для того чтобы определить, с какой степенью вероятности мы можем утверждать, что средние величины одного класса существенно отличаются от аналогичных величин другого класса, нужно сделать расчет достоверности различий. Что же для этого необходимо?
1. Вычислить средние арифметические величины для каждого класса в отдельности по следующей формуле:
где Xi– значение отдельного измерения; n – общее число измерений в классе (количество тестируемых). Проставив в формулу фактические значения, получаем среднее арифметическое значение для каждого класса. Следует убедиться в статистической достоверности различий между рассчитанными среднеарифметическими значениями.
2. Вычислить отдельно в каждом классе стандартное отклонение σ по следующей формуле:
где Ximax – наибольший показатель; Ximin – наименьший показатель; K – табличный коэффициент (см. табл. 1).
Таблица 1
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
– |
– |
1,13 |
1,69 |
2,06 |
2,33 |
2,53 |
2,70 |
2,85 |
2,97 |
|
10 |
3,08 |
3,17 |
3,26 |
3,34 |
3,41 |
3,47 |
3,53 |
3,59 |
3,64 |
3,69 |
|
20 |
3,74 |
3,78 |
3,82 |
3,86 |
3,90 |
3,93 |
3,96 |
4,00 |
4,03 |
4,06 |
|
30 |
4,09 |
4,11 |
4,14 |
4,16 |
4,19 |
4,21 |
4,24 |
4,26 |
4,28 |
4,30 |
|
40 |
4,32 |
4,34 |
4,36 |
4,38 |
4,40 |
4,42 |
4,43 |
4,45 |
4,47 |
4,48 |
|
50 |
4,50 |
4,51 |
4,53 |
4,54 |
4,56 |
4,57 |
4,59 |
4,60 |
4,61 |
4,63 |
|
60 |
4,64 |
4,65 |
4,66 |
4,68 |
4,69 |
4,70 |
4,71 |
4,72 |
4,73 |
4,74 |
|
70 |
4,76 |
4,76 |
4,78 |
4,79 |
4,80 |
4,81 |
4,82 |
4,82 |
4,84 |
4,84 |
|
80 |
4,85 |
4,86 |
4,87 |
4,88 |
4,89 |
4,90 |
4,91 |
4,92 |
4,92 |
4,93 |
|
90 |
4,94 |
4,95 |
4,96 |
4,96 |
4,97 |
4,98 |
4,99 |
4,99 |
5,00 |
5,01 |
|
100 |
5,02 |
5,02 |
5,03 |
5,04 |
5,04 |
5,05 |
5,06 |
5,06 |
5,07 |
5,08 |
|
110 |
5,08 |
5,09 |
5,10 |
5,10 |
5,11 |
5,11 |
5,12 |
5,13 |
5,13 |
5,14 |
Порядок вычисления стандартного отклонения:
а) определить отдельно в каждом классе Ximax, Ximin;
б) определить число измерений в каждом классе (n);
в) найти по табл. 1 значение коэффициента K, который соответствует числу измерений в каждом классе. Например, если измерений 18, то для этого в левом крайнем столбце под индексом n находим число 10, а в верхней строке – 8, на пересечении этих строк – 3,64, что соответствует значению коэффициента K при 18 тестируемых;
г) подставить полученные значения в формулу и произвести необходимые вычисления.
3. Вычислить стандартную ошибку среднего арифметического значения m по формуле
когда n<30;
когда n≥30.
Для нашего примера подходит первая формула, так как n<30.
4. Вычислить среднюю ошибку разности по формуле
5. По специальной таблице определить достоверность различий (табл. 2). Для этого полученное значение t сравниваем с граничным значением при 5%-ном уровне значимости (p=0,05) при числе степеней свободы f=n1+n2–2, где n1 и n2 – общее число индивидуальных результатов соответственно в каждом классе. Если окажется, что полученное в ходе тестирования t больше граничного значения (p=0,05), то различия между средними арифметическими значениями двух классов считаются достоверными при 5%-ном уровне значимости. В случае когда полученное t меньше граничного значения (p=0,05), считается, что различия недостоверны и разница в среднеарифметических показателях каждого класса имеет случайный характер.
Таблица 2
| Степень свободы |
p=0,05 | Степень свободы |
p=0,05 | Степень свободы |
p=0,05 |
|---|---|---|---|---|---|
| 1 | 12,71 | 13 | 2,16 | 25 | 2,06 |
| 2 | 4,30 | 14 | 2,15 | 26 | 2,05 |
| 3 | 3,18 | 15 | 2,13 | 27 | 2,05 |
| 4 | 2,78 | 16 | 2,12 | 28 | 2,05 |
| 5 | 2,57 | 17 | 2,11 | 29 | 2,04 |
| 6 | 2,45 | 18 | 2,10 | 30 | 2,04 |
| 7 | 2,37 | 19 | 2,09 | 40 | 2,02 |
| 8 | 2,31 | 20 | 2,08 | 50 | 2,01 |
| 9 | 2,26 | 21 | 2,08 | 60 | 2,00 |
| 10 | 2,23 | 22 | 2,07 | 80 | 1,99 |
| 11 | 2,20 | 23 | 2,07 | 100 | 1,98 |
| 12 | 2,18 | 24 | 2,06 | 120 | 1,98 |
Граничное значение при 5%-ном уровне значимости (p=0,05) определяется следующим образом:
а) вычислить число степеней свободы (f=n1+n2–2);
б) найти по табл. 2 граничное значение (p=0,05) для соответствующей степени свободы (f).
Таким же образом можно проверить достоверность различий среднеарифметических показателей учащихся одного класса в начале и конце учебного года. В данном случае оба цифровых ряда взаимно связаны (повторное измерение в одном и том же классе). Поэтому t рассчитывают другим способом. Сначала определяют разницу между индивидуальными вариантами:
где – среднеарифметическое значение в начале учебного года,
– в конце учебного года.
6. Произвести расчет среднего квадратического отклонения разностей (стандартного отклонения) по формуле
7. Рассчитать среднюю ошибку разности по формуле 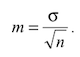
Статистическая достоверность различий:
Таким образом, были рассмотрены два примера, в которых проводилась оценка различий показателей физического развития и физической подготовленности в небольших – до 30 человек – независимых или взаимно связанных группах.
В педагогических исследованиях различия считаются достоверными при 5%-ном уровне значимости, т.е. при утверждении того или иного положения допускается ошибка не более чем в 5 случаях из 100. В случае если расчетное значение t меньше граничного значения t (p=0,05), различия между полученными в исследовании средними арифметическими значениями считаются недостоверными – значит, недостаточно оснований для того, чтобы говорить о положительной динамике результатов учащихся в течение учебного года (p>0,05).
Таблица 3
| Показатели | Оценка в баллах | Границы |
|---|---|---|
| Очень высокий | 7 | Выше x+2σ |
| Высокий | 6 | От x+1σ до x+2σ |
| Выше среднего | 5 | От x-0,5σ до x+1σ |
| Средний | 4 | От x-0,5σ до x+0,5σ |
| Ниже среднего | 3 | От x–1σ до x–0,5σ |
| Низкий | 2 | От x–2σ до x–1σ |
| Очень низкий | 1 | Ниже x–2σ |
Примечание. Для тестов, связанных с бегом на скорость, расчет уровней возможной градации оценок ведется следующим образом: например, очень высокий показатель – 7 баллов, низкий показатель – 2 балла (x–2σ) и т.д.
Для каждого учащегося на основе, разработанной в баллах шкалы оценки, определяется суммарный показатель в зависимости от количества выполненных тестов. В табл. 4 в качестве примера представлены возможные градации суммарной оценки в баллах показателей физического развития и физической подготовленности учащихся.
Таблица 4
| Показатели | Физическое развитие (5 показателей) |
Физическая подготовленность (8 показателей) |
|---|---|---|
| оценка в баллах | оценка в баллах | |
| Очень высокий | 35 | 56 |
| Высокий | 30–34 | 48–55 |
| Выше среднего | 25–29 | 40–47 |
| Средний | 20–24 | 32–39 |
| Ниже среднего | 15–19 | 24–31 |
| Низкий | 10–14 | 16–23 |
| Очень низкий | Меньше 10 | Меньше 16 |
Таким образом, учитель физической культуры, ориентируясь на данные таблицы и индивидуальные показатели учащихся, легко и быстро может определить уровень физического развития и физической подготовленности каждого, темпы прироста результатов за четверть, полугодие и учебный год.
Результаты мониторинговых исследований позволяют получить объективную оценку уровня теоретико-методических знаний учащихся, отслеживать динамику показателей физического развития и физической подготовленности учащихся и тем самым могут использоваться как эффективное средство осуществления индивидуального подхода к физическому воспитанию, поиска путей оптимизации учебного процесса по физической культуре в школе и сохранения здоровья каждого школьника.
Ильдар Латыпов ,
к.п.н., доцент Педагогического института физической культуры, Москва
На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.
Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.
Например,
- $y = textcolor{blue}{5}x + color{green}{10}$ – линейная функция
- $color{blue} k = 5$
- $color{green} b = 10$.
График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.
Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$
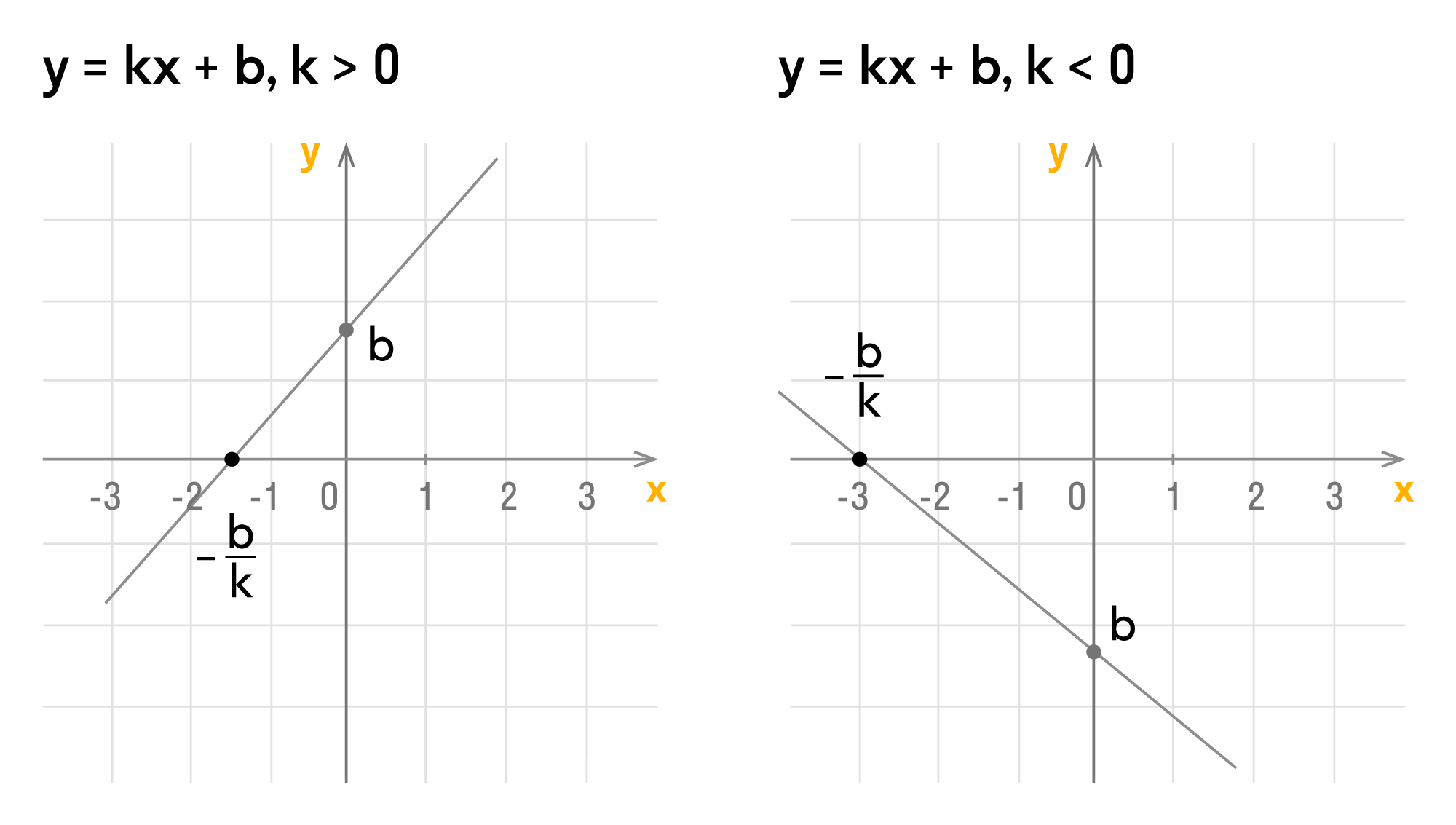
При $k > 0$ угол между графиком и осью $Ox$ меньше $90 degree$ (острый)
При $k < 0$ угол между графиком и осью $Ox$ больше $90 degree$ (тупой)
Коэффициент b
Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.
Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.
- Если $b > 0$, график сдвинут вверх,
- если $b < 0$, то график сдвинут вниз.
На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).
Частные случаи. b = 0
Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.
Подставим в формулу $x = 0$, получим: $$y = k times 0$$
Значит, график будет проходить через начало координат $O(0;0)$.
Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.
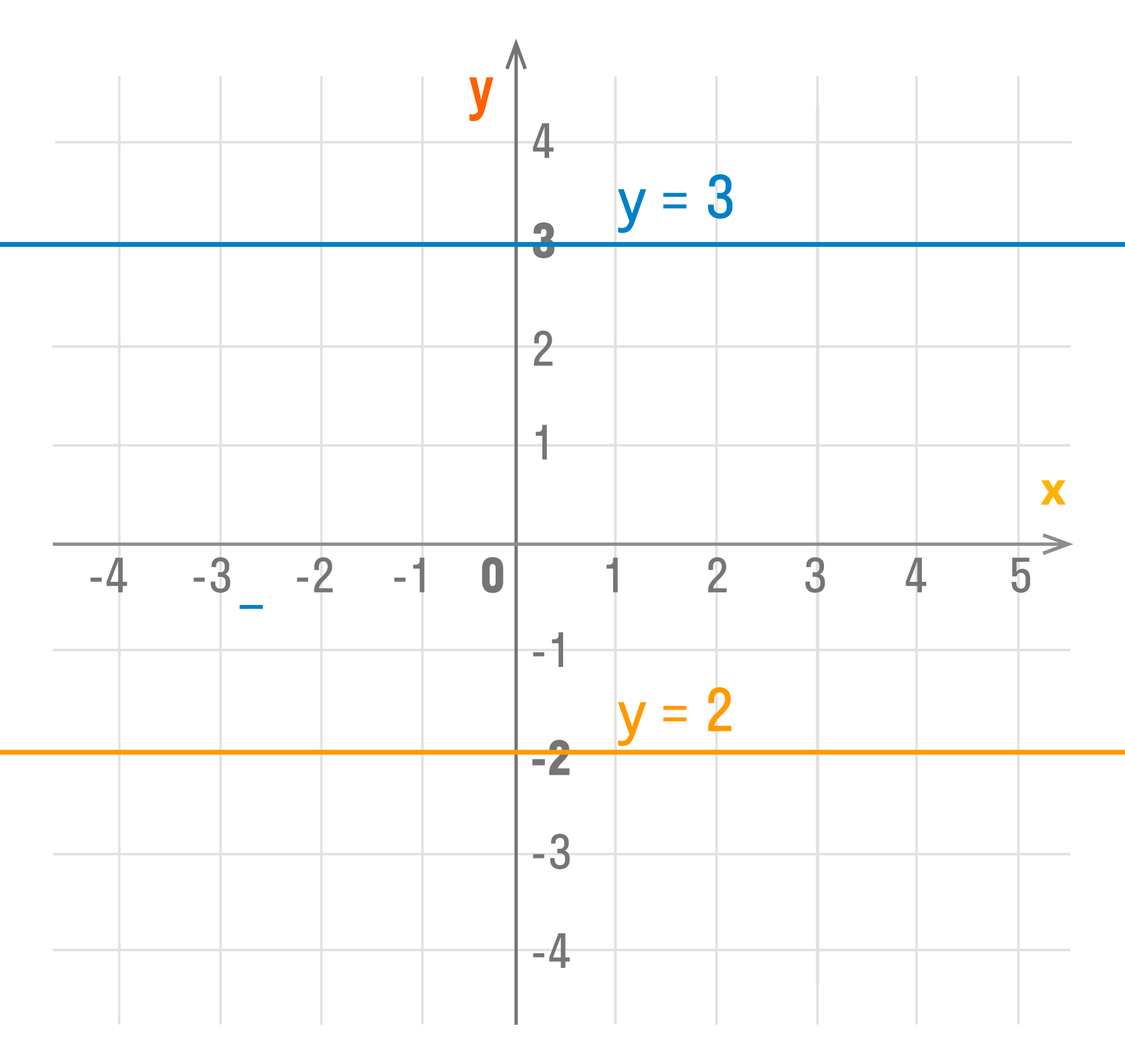
k = 0
Если коэффициент $k = 0$, угол наклона также будет равен $0$.
Функция при этом принимает вид $y = 0 times x + b$, то есть $y = b$.
Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.
Таблица