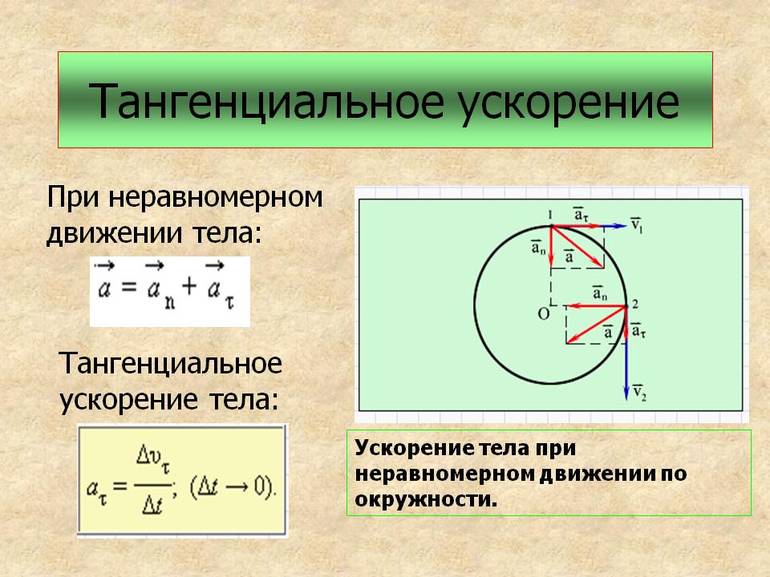
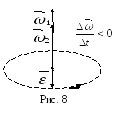Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
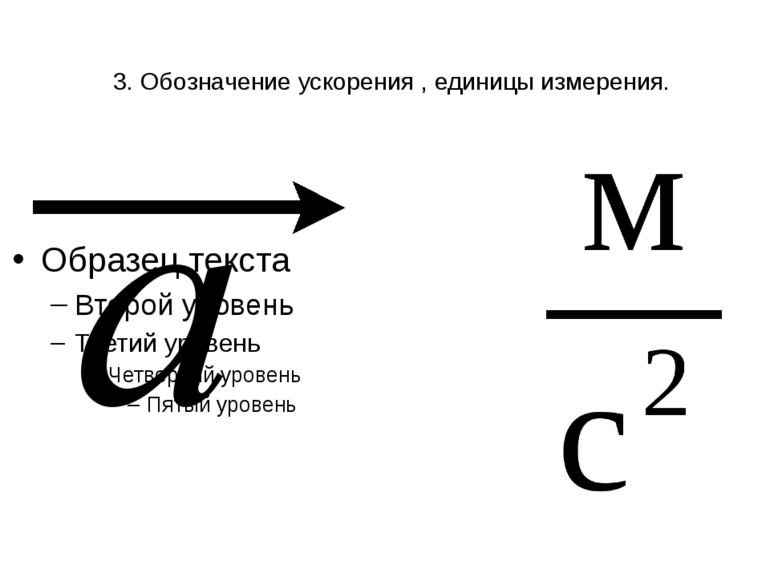
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
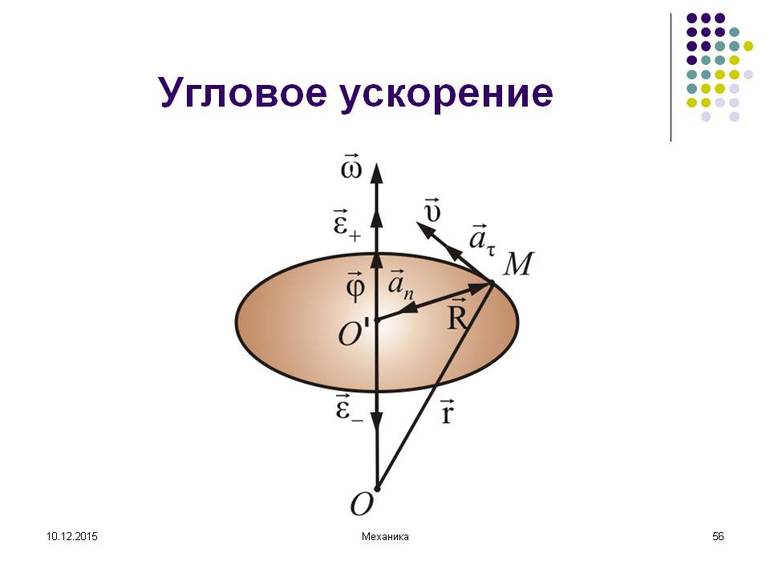
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
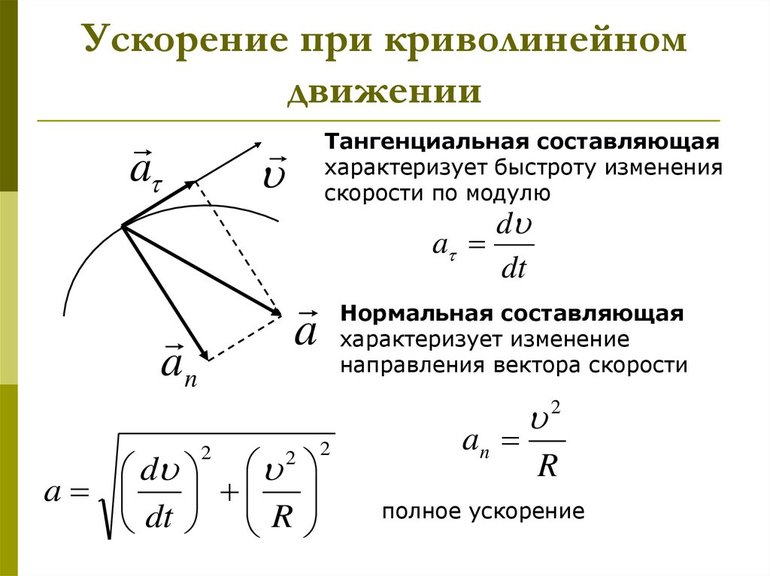
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.
Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2.
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t3. Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м2/с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V2 / R = R * (0,6 * 102 — 1)2 / 0,2 = 696 м/с2. Отсюда полное ускорение будет равняться: a = √ 242 + 6962 = 697 м/с2.
- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V2. В итоге должно получиться выражение: dV / V2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
Движение
тела характеризуется скоростью и
ускорением, которые могут изменяться
во времени. Пусть материальная точка
движется по плоской криволинейной
траектории с переменной по величине и
направлению скоростью (рис. 4). Для
характеристики степени криволинейности
вводится понятие радиуса кривизны в
данной точке траектории.
Радиусом
кривизны
R
траектории
называют радиус окружности, которая
сливается с криволинейной траекторией
на бесконечно малом ее участке.
В данной
точке траектории касательная всегда
перпендикулярна радиусу кривизны.
П
и скорость, и ускорение меняются по
величине и направлению.
Мы знаем,
что ускорение тела при движении есть .
Вектор
скорости
можно представить как произведение
модуля скорости
и некоторого единичного вектора
,
сонаправленного с вектором линейной
скорости
,
направленного по касательной к траектории.
Таким
образом, полное ускорение материальной
точки при криволинейном движении можно
представить в виде суммы двух слагаемых.
Первое слагаемое
.
Вектор
направлен по касательной к траектории
и называется тангенциальным
или касательным ускорением. Его модуль
равен
,
поэтому
характеризует быстроту изменения
скорости криволинейного движения только
по величине, так как вектор
не изменяется.
Следовательно,
можно заключить, что
— тангенциальное ускорение, характеризует
изменение скорости по величине и
направлено по касательной к траектории.
Второе
слагаемое
называется нормальным ускорением.
Так
как вектор
сонаправлен с вектором
,
который определяет изменение направления
вектора линейной скорости, то он
характеризует изменение скорости
криволинейного движения по направлению.
перпендикулярно
скорости, направлено вдоль радиуса
кривизны траектории к центру окружности.
Его называют нормальным, радиальным
или центростремительным ускорением.
Можно
доказать, что
.
Полное
ускорение материальной точки при
криволинейном движении характеризует
быстроту изменения скорости как по
величине, так и по направлению (рис.5).
,
.
4. Угловая скорость и угловое ускорение.
П
тела на некоторый угол можно задать в
виде отрезка, длина которого равна ,
а направление совпадает с осью, вокруг
которой производится поворот. Направление
поворота и изображающего его отрезка
связано правилом правого винта.
В
математике показывается, что очень
малые повороты можно рассматривать как
векторы, обозначаемые символами
или
.
Направление вектора поворота связывается
с направлением вращения тела;
— вектор элементарного поворота тела —
является псевдовектором, так как не
имеет точки приложения.
При
вращательном движении твердого тела
каждая точка движется по окружности,
центр которой лежит на общей оси вращения
(рис. 6). При этом радиус-вектор R,
направленный от оси вращения к точке,
поворачивается за время t
на некоторый угол .
Для характеристики вращательного
движения вводится угловая скорость и
угловое ускорение.
У
гловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:
Угол
в 1 радиан – это центральный угол, длина
дуги которого равна радиусу окружности;
360о
=
2
рад.
Направление
угловой скорости задается правилом
правого винта:
вектор угловой скорости сонаправлен с
вектором
,
то есть с поступательным движением
винта, головка которого вращается в
направлении движения точки по окружности.
Линейная
скорость точки связана с угловой
скоростью:
.
В
векторной форме
.
Если
в процессе вращения угловая скорость
изменяется, то возникает угловое
ускорение.
Угловое
ускорение
– векторная величина, равная первой
производной угловой скорости по времени.
Вектор угловой скорости сонаправлен с
вектором элементарного изменения
угловой скорости
,
происшедшего за время dt:
При
ускоренном движении вектор
параллелен
(рис.
7), при замедленном – противонаправлен
(рис. 8).
Угловое
ускорение возникает в системе только
тогда, когда происходит изменение
угловой скорости, то есть когда линейная
скорость движения изменяется по величине.
Изменение же скорости по величине
характеризует тангенциальное ускорение.
Найдем
связь между угловым и тангенциальным
ускорениями:
.
Изменение
направления скорости при криволинейном
движении характеризуется нормальным
ускорением
:
.
Таким
образом, связь между линейными и угловыми
величинами выражается следующими
формулами:
.
Типы
вращательного движения:
а)
переменное
–
движение, при котором изменяются
и
:
б)
равнопеременное
– вращательное движение с постоянным
угловым ускорением:
;
в)
равномерное
–
вращательное
движение с постоянной угловой скоростью:
.
Равномерное
вращательное движение можно характеризовать
периодом
и частотой вращения
.
Период
– это время, за которое тело совершает
один полный оборот.
,
[T]
= c.
Частота
вращения
– это число оборотов совершаемых за
единицу времени.
,
[]
= c-1.
За
один оборот: ,
,
.
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
В этой статье мы обсудим, как найти тангенциальное ускорение от различных вращательных движений, решая некоторые задачи с примерами.
Тангенциальное ускорение — это изменение тангенциальной скорости объекта на круговой траектории, перпендикулярной центростремительной силе, действующей внутрь.
Как найти тангенциальное ускорение из угловой скорости?
Вычислив изменение переменной угловой скорости во времени, мы можем найти угловое ускорение и, следовательно, тангенциальное ускорение объекта.
Тангенциальное ускорение можно определить, измерив разницу между тангенциальной скоростью, которая равна произведению угловой скорости на радиус кругового пути, пройденного объектом.
Рассмотрим объект, путешествующий с угловая скорость ω по круговой дорожке радиуса ‘r’.
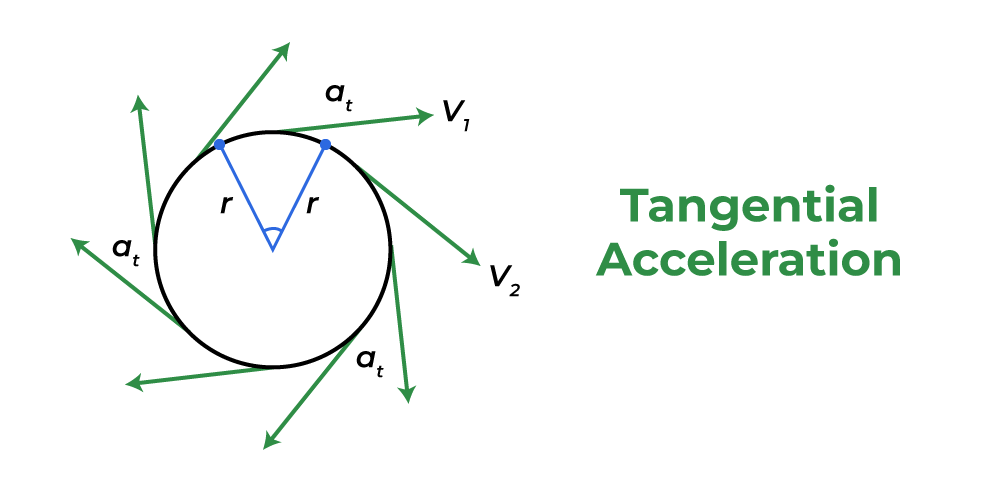
Пусть «s» — смещение объекта за время «t», а «θ» — угол, образованный за счет смещения объекта. Следующий рисунок представляет то же самое.
По геометрии длина дуги s круга, охваченного объектом за время t, будет равна
s = г1 — (XNUMX)
Здесь, в приведенном выше уравнении, есть две переменные. Местоположение объекта смещается по круговой траектории, составляющей угол θ в диапазоне 0–360°.0. Следовательно, мы можем переписать приведенное выше уравнение как
Δs=rΔθ
При делении обеих частей на переменную времени имеем
Δs/θt=rΔθ/Δt
Тангенциальная скорость объекта — это смещение объекта между двумя интервалами времени. Это то же самое, что v=Δs/Δt}; а угловое смещение объекта при изменении времени равно угловой скорости объекта. Следовательно, предыдущее уравнение принимает вид
v=rω — (2)
Где v — тангенциальная скорость
Если ω является угловая скорость объекта, то угловое ускорение объекта будет
α = Δω/ Δt — (3)
Где α — угловое ускорение объекта.
Тангенциальное ускорение частицы — это изменение радиальной скорости объекта во времени, изменяющееся при изменении направления скорости.
Приведенное выше уравнение показывает взаимосвязь между тангенциальным ускорением и угловой скоростью объекта. Тангенциальное ускорение равно отношению изменения угловых скоростей объекта во времени и прямо пропорционально радиусу кругового пути, пройденного объектом.
Подробнее о Угловое ускорение.
Как найти тангенциальное ускорение при круговом движении?
Центростремительная сила удерживает тело в круговом движении, а направление тангенциальной скорости остается перпендикулярным этой силе.
Тангенциальное ускорение при круговом движении — это изменение скорости, вызванное изменением направления углового ускорения объекта.
Рассмотрим объект, движущийся в круговое движение под действием силы равна центростремительной силе.
Ф=Фc
Пусть «r» — радиус окружности, а v и a — радиальная скорость и радиальное ускорение соответственно.
ма=мв2/r
а=в2/ г — (6)
Подставляя уравнение (2) в приведенное выше уравнение, мы имеем
а=rω2 -(Один)
Это радиальное ускорение объекта, а тангенциальное ускорение объекта будет
at=dv/dt=rdω/dt=rα
Где ω — угловая скорость, а
α — угловое ускорение объекта
Полное ускорение объекта при круговом движении будет векторной суммой тангенциального ускорения и радиального ускорения.
А также,
Следовательно,
Как найти тангенциальное ускорение без учета времени?
Компания тангенциальное ускорение зависит от углового ускорение объекта.
Тангенциальное ускорение — это коэффициент изменения тангенциальной скорости, возникающей из-за изменения направления пути объекта во времени.
Ссылаясь на приведенное выше уравнение № (5), мы можем написать
at=rα—(10)
Это уравнение показывает связь между тангенциальной ускорение и угловой ускорение тела не зависит от времени.
Как найти тангенциальное ускорение маятника?
Маятник совершает гармонические колебания, составляющие угол θ по длине струны.
Возвращающая сила, действующая на струну, возвращает маятник в исходное положение, действующее по касательной к дуге. На его основе можно найти тангенциальное ускорение маятника.
Рассмотрим маятник в СГМ. Нить длины «L» прикреплена к грузу массой «m». Пусть ‘s’ будет смещением боба из-за гармонического движения.
По длине струны действует сила, равная mgCosθ, которая компенсируется натяжением струны. Возвращающая сила, действующая на груз, определяется выражением
F=-mgSinθ
ма=-mgSinθ
Для малых углов
а = гθ
Угол θ можно рассчитать, измерив длину дуги и разделив ее на длину струны.
θ = с/л
Следовательно, приведенное выше уравнение становится
а=гс/л
Тангенциальное ускорение маятника равно ускорению свободного падения и перемещению груза на длину нити.
Как найти тангенциальное ускорение с учетом времени?
Тангенциальная скорость будет увеличиваться со временем, если скорость тангенциального ускорения положительна.
Тангенциальное ускорение можно рассчитать, найдя разницу в радиальной скорости объекта, которая, очевидно, меняется, поскольку направление объекта с угловой скоростью продолжает меняться со временем.
Это дается формулой
at=двt/ дт
Где vt это радиальная скорость
Подробнее о Как найти ускорение на графике скорости: задачи и примеры.
Часто задаваемые вопросы
Задача 1: Объект движется с ускорением по окружности радиусом 10 м. Угловая скорость объекта увеличивается до 6 м/с с 4 м/с между временными интервалами в 4 секунды. Вычислите тангенциальное ускорение тела.
Данный: r = 10 м
ω1= 4 м / с
ω2= 6 м / с
Δt=4 сек
Поэтому тангенциальное ускорение равно
=10 х (6-4)/4
=10 х 2/4=5 м/с2
Следовательно, тангенциальное ускорение тела равно 5 м/с.2.
Задача 2: Рассчитайте тангенциальное ускорение и угловое ускорение мяча, движущегося по круговой траектории радиусом 5 метров со скоростью от 2 м/с до 4 м/с за 4 секунды.
Данный: V1= 2 м / с
V2= 4 м / с
Т=4с
Р=5м
Касательное ускорение равно
Поскольку, аt=rα
α = аt/r
α = 0.5 м/с2/5м=0.1 радиан/с2
Компания угловое ускорение мяча 0.1 радиан/с2.
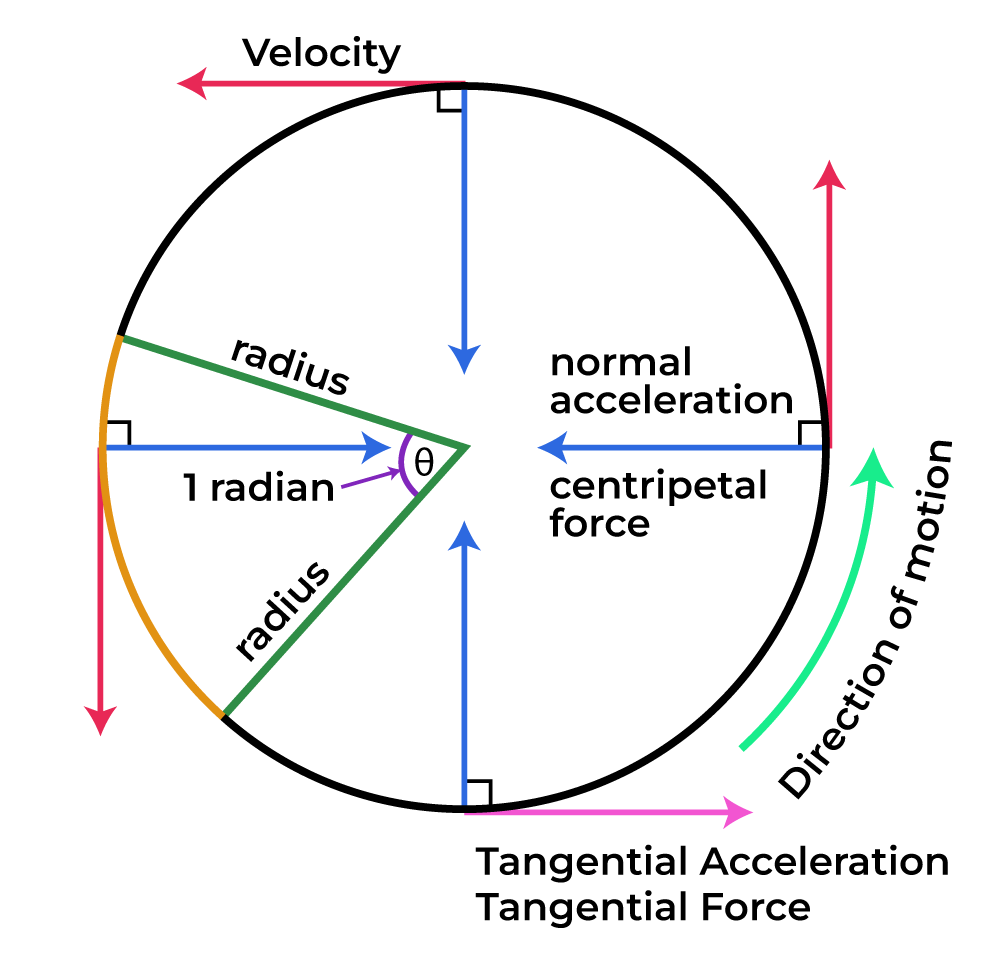
Tangential acceleration is the rate at which a tangential velocity varies in the rotational motion of any object. It acts in the direction of a tangent at the point of motion for an object. The tangential velocity also acts in the same direction for an object undergoing circular motion. Tangential acceleration only exists when an object travels in a circular path. It is positive if the body is rotating at a faster velocity, negative when the body is decelerating, and zero when the body is moving uniformly in the orbit.
Tangential Acceleration
Tangential acceleration is similar to linear acceleration, however, it is only in one direction. This has something to do with circular motion. Tangential acceleration is therefore the rate of change of a particle’s tangential velocity in a circular orbit. It always points to the tangent of the body’s route.
Tangential acceleration works when an object moves in a circular path. Tangential acceleration is similar to linear acceleration, but it is not the same as straight-line linear acceleration. If an item moves in a straight line, it is linearly accelerating.
A car, for example, speeding around a bend in the road. The automobile is accelerating tangentially to the path’s bend.
Also Read: What is Acceleration?
Tangential Acceleration Formula
The tangential acceleration is denoted by the symbol at. Its unit of measurement is the same as linear acceleration, that is, meters per square second (m/s2). Its dimensional formula is given by [M0L1T-2]. Its formula is given by the product of the radius of a circular path and the angular acceleration of the rotating object.
at = r α
where,
- at is the tangential acceleration,
- r is the radius of circular path,
- α is the angular acceleration.
The above expression gives the relation between tangential acceleration and angular acceleration.
Now, in terms of angular velocity and time, the formula is given by,
at = r (ω/t)
where,
- at is the tangential acceleration,
- ω is the angular velocity,
- t is the time taken.
In terms of angular displacement and time, the formula is given by,
at = r (θ/t2)
where,
- at is the tangential acceleration,
- θ is the angular displacement or angle of rotation,
- t is the time taken.
Following are the various cases possible for different values of Tangential Acceleration:
- When at is greater than Zero: The object has an accelerated motion, and the magnitude of velocity will increase with time.
- When at is Less than Zero: The object has a deaccelerated or slow motion, and the magnitude of velocity will decrease with time.
- When at is Equal to Zero: The object has a uniform motion, and the magnitude of velocity will remain constant.
Read More: Uniformly Accelerated Motion
Solved Examples on Tangential Acceleration
Example 1: Calculate the tangential acceleration if an object is undergoing circular motion for radius 5 m and angular acceleration 2 rad/s2.
Solution:
We have,
r = 5
α = 2
Using the formula we get,
at = r α
= 5 (2)
= 10 m/s2
Example 2: Calculate the tangential acceleration if an object is undergoing circular motion for a radius of 12 m and angular acceleration of 0.5 rad/s2.
Solution:
We have,
r = 12
α = 0.5
Using the formula we get,
at = r α
= 12 (0.5)
= 6 m/s2
Example 3: Calculate the angular acceleration if an object is undergoing circular motion for radius 20 m and tangential acceleration 40 m/s2.
Solution:
We have,
r = 20
at = 40
Using the formula we get,
at = r α
α = at/r
= 40/20
= 2 rad/s2
Example 4: Calculate the angular acceleration if an object is undergoing circular motion for radius 2 m and tangential acceleration 20 m/s2.
Solution:
We have,
r = 2
at = 20
Using the formula we get,
at = r α
α = at/r
= 20/2
= 10 rad/s2
Example 5: Calculate the radius if an object is undergoing circular motion for an angular acceleration of 4 rad/s2 and tangential acceleration of 20 m/s2.
Solution:
We have,
α = 4
at = 20
Using the formula we get,
at = r α
r = at/α
= 20/4
= 5 m
FAQs on Tangential Acceleration
Question 1: What are the values of radial and tangential acceleration when the motion of a particle is uniformly accelerated?
Answer:
Even though there is no tangential acceleration, the centripetal acceleration must be present to alter the direction of velocity at all times, and the centripetal acceleration is the net acceleration in this instance. This is an example of uniform circular motion.
Thus, If ar and at represent radial and tangential acceleration then, ar ≠ 0 and at = 0.
Question 2: What is Tangential Acceleration?
Answer:
Tangential acceleration is the rate at which a tangential velocity varies in the rotational motion of any object. It acts in the direction of a tangent at the point of motion for an object.
Question 3: What is the value of Tangential Acceleration in Uniform Circular Motion?
Answer:
The tangential acceleration is zero for uniform circular motion. In a uniform circular motion, angular velocity remains constant thus tangential acceleration = 0.
Read More: Uniform Circular Motion
Question 4: What is the SI Unit of Tangential Acceleration?
Answer:
The SI Unit of Tangential Acceleration is m/s2.
Question 5: What is the relation between Tangential Acceleration and Angular Acceleration?
Answer:
The Tangential Acceleration formula is given by the product of the radius of a circular path and the angular acceleration of the rotating object.
at = r α
where,
- at is the tangential acceleration,
- r is the radius of circular path,
- α is the angular acceleration.
Last Updated :
19 Dec, 2022
Like Article
Save Article
Угловое ускорение – что это?
Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.
Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
- (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
- (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
- (omega=2pinu), где (nu) – числом оборотов в единицу времени.
Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)
Связь между угловой скоростью и нормальным (центростремительным) ускорением
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.
Центростремительное ускорение определяется по формуле:
(a_n=frac{V^2}R),
где (V) – скорость движения, (R) – радиус окружности.
Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})
Итак, формула связывающая эти две величины:
(a_n=omega^2R)
Основные формулы для расчета углового ускорения
Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.
(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)
Угловое ускорение маховика
(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})
Тангенциальное ускорение
Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})