Касательное и нормальное ускорения точки
Касательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению
Проекция ускорения на касательную и на нормаль
Если движение точки задано в векторной или в координатной форме, то часто встречается необходимость определить проекции ускорения на касательную и главную нормаль к траектории точки в том ‘ месте, где в данное мгновение находится точка (рис. 91, а).
При естественной форме определения движения точки сначала определяют проекции ускорения на касательную и на нормаль, а затем уже по этим проекциям находят величину и направление полного ускорения точки.
Проекцию ускорения точки на касательную к ее траектории называют касательным ускорением, или тангенциальным ускорением (от латинского слова tangens—касающийся), и обозначают aN.
Проекцию ускорения на нормаль называют нормальным ускорением и обозначают ar.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. В таком случае над аr и aN ставят стрелку, указывающую на их векторный характер.
Разложение ускорения по касательной и нормали имеет физический смысл: касательная составляющая ускорения направлена по касательной (как и скорость), а потому не может повлиять на направление скорости, но влияет на ее величину; составляющая ускорения по нормали направлена перпендикулярно к скорости, а потому не может повлиять на величину скорости, но влияет на ее направление.
Касательное ускорение равно первой производной от величины скорости по времени:
Касательное ускорение
Пусть точка M движется по траектории, расположенной в плоскости хОу.
Проведем касательную и нормаль к кривой в точке M (рис. 91, б), нанесем на чертеж вектор ускорения 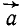
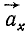
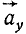
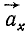
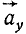
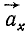
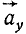
Составляющие ускорения 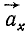
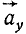
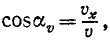
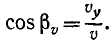
Подставляя значения направляющих косинусов, получаем
По формуле (68) удобно вычислять касательное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Можно дать еще другой изящный вывод формулы (68) тангенциального ускорения, для чего спроецировать на касательную вектор полного ускорения, не раскладывая его предварительно по осям декартовых координат. В самом деле, тангенциальное ускорение равно проекции полного ускорения на касательную (рис. 91, а):
ar = a cos δ,
но угол δ, как внутренний угол треугольника, равен внешнему αа без другого внутреннего αυ, поэтому:
cos δ = cos (αа—aυ) = cos αа cos aυ + sin αа sin aυ
или, так как αа = 90°- βa и aυ = 90°-βυ,
cos δ = cos αа cos aυ + cos βa cos βυ .
Подставляя сюда вместо направляющих косинусов их выражения (67) n (62′), получим
Напомним, что в числителе этой формулы проекции имеют свой знак, а знаменатель определяется по (64), т. е. существенно положителен.
Задача №1
Движение точки задано в декартовых координатах уравнениями:
x=21,2 sin2 t, y=21,2 cos2 t
Определить касательное ускорение точки (см. задачу № 36, стр. 132).
Решение. Дифференцируя уравнения движения, найдем υx = 21,2 sin 2t, υy = -21,2 sin 2t. Определим теперь полную скорость:
Дифференцируя уравнения движения вторично, найдем
αx = 42,2 cos 2t, αy = -42,4 cos 2t.
Касательное ускорение определим по формуле (68):
Ответ. Касательное ускорение равно 60 cos 2t.
Задача №2
Точка M движется в системе координат хОу согласно уравнениям x=r cos πt, y=r sin πt. Найти касательное ускорение точки М.
Решение. Проекции скорости и ускорения на оси координат, а также и полная скорость точки M были уже нами получены при решении задачи № 44 (см. стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):
Ответ. Касательное ускорение равняется нулю.
Для случая задания движения в естественной форме преобразуем формулу (68) следующим образом:
и, сокращая на υ, найдем касательное ускорение
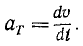
Принимая во внимание (53), можно придать этой формуле несколько иной вид:
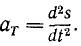
Итак, касательное ускорение—это проекция ускорения точки на касательную к траектории, равная первой производной от величины скорости по времени. Чтобы получить касательное ускорение в векторном выражении, нужно его умножить на единичный вектор касательной:
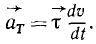
Как уже было сказано, касательное ускорение не может изменить направления скорости, оно характеризует быстроту изменения величины скорости, т. е. соответствует изменению вектора скорости вдоль его направления.
Если с течением времени величина скорости увеличивается, то касательное ускорение направлено в ту же сторону, что и скорость. Такое движение называют ускоренным.
Если же величина скорости уменьшается, то касательное ускорение направлено в сторону, противоположную скорости. Такое движение называют замедленным.
Каждое из этих движений называют переменным движением.
Если величина скорости точки постоянна, то производная 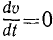
Обратное заключение можно сделать лишь с некоторой оговоркой: если касательное ускорение постоянно равняется нулю, то, следовательно, величина скорости постоянна и движение равномерно; если же касательное ускорение точки равняется нулю не в течение всего рассматриваемого промежутка времени, а только в какое-то мгновение, то движение точки не является равномерным, и равенство 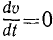
При равномерном движении точки по любой траектории
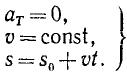
Формулы (70) справедливы только для равномерного движения точки и неприменимы при других движениях.
Равнопеременное движение точки
Из переменных движений точки в задачах наиболее часто встречается равнопеременное движение — такое движение, при котором касательное ускорение остается постоянным.
При равнопеременном движении точки по любой траектории
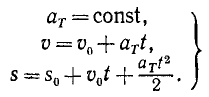
Формулы (71) справедливы только для равнопеременного движения и неприменимы при других движениях. Они даны здесь без вывода и известны из элементарной физики. Вывод этих формул приведен в решении задачи № 48.
Задача №3
Точка А начала двигаться с начальной скоростью υ0= 1 м/сек и с ускорением aT =2 м/сек2. Через одну секунду следом за точкой А по той же траектории с такой же начальной скоростью и с таким же касательным ускорением стала двигаться точка В. Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.
Решение. Определим сначала уравнение движения точек. Нам дано, что
Разделяя переменные и интегрируя, получим
υ = aTt + C1
Постоянную C1 определим из начальных данных:
υ0 = aT . 0 + C1; C1=υ0
Следовательно,
υ = υ0 + aTt.
Написав υ по (53), разделяя переменные и интегрируя, найдем
где
С2 = s0 = 0.
Подставляя вместо υ0 и аT заданные величины, найдем расстояние (в м), пройденное точкой А за время t:
В то же мгновение t расстояние, пройденное точкой В, будет меньше, так как точка В будет находиться в пути лишь t—1 сек. Для точки В
Расстояние между A и B найдем как разность пройденных ими путей:
Это расстояние растет пропорционально времени, хотя точка В во времени не отстает от точки А и каждую точку траектории проходит через 1 сек после того, как через нее прошла точка А.
Графики движения точек А и В изображаются одинаковыми параболами (рис. 92), но парабола, представляющая движение точки В, смещена по оси времени относительно параболы, представляющей движение точки А, на 1 сек вправо. Чтобы определить расстояние (в м) между А и В в какое-либо мгновение, надо восставить перпендикуляр к оси времени в точке, соответствующей этому мгновению, и измерить расстояние по вертикали между параболами. Чтобы определить интервал времени (в сек) между прохождениями точками А и В какой-либо точки К траектории, надо восставить перпендикуляр к оси расстояний в точке, соответствующей расстоянию точки К от начала отсчета, и измерить расстояние по горизонтали между параболами. Графики наглядно показывают, что точка В отстает от точки А по расстоянию, так как А В непрерывно увеличивается, но не отстает по времени, и точка В проходит каждый отрезок траектории за такое же время, как и точка А.
Рис. 92
Ответ. SA— SB = 2t м.
Нормальное ускорение равно отношению квадрата скорости точки к радиусу кривизны траектории:
Нормальное ускорение
Чтобы получить формулы нормального ускорения, мы опять воспользуемся тем, что проекция вектора на ось равна сумме проекций его составляющих на ту же ось, и определим aN как алгебраическую сумму проекций составляющих ax и ay на нормаль к траектории точки. Выберем за положительное направление нормали то, которое получается от поворота положительного направления касательной на прямой угол против хода часов (см. рис. 91) в сторону вогнутости кривой.
Как видно из чертежа (см. рис. 91, б)
aN = ay cos αυ—ax cos βυ.
Подставляем значения (62) направляющих косинусов:
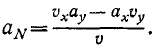
По этой формуле удобно вычислять нормальное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).
Эту же формулу (72) можно получить, спроецировав полное ускорение а на нормаль Mn (рис. 91, а):
aN = a sin δ = a sin (αα—αυ)
или
aN=a (sinαα cos αυ -cos αα sin αυ).
Подставляя эти значения и сокращая на а, получим:
Задача №4
Движение точки задано уравнениями X= 21,2 sin2 t, у= 212 cos2 t. Определить нормальное ускорение точки.
Решение. Дифференцируя эти же уравнения движения при решении задачи № 36 (см. стр. 132), мы уже определили нужные нам величины: υx, υy, υ, ax, ау. Подставляя их в формулу (72), найдем
Ответ. Нормальное ускорение равно нулю.
Задача №5
Точка M движется согласно уравнениям x= r cos πt, y= r sin πt. Найти нормальное ускорение точки М.
Решение. Дифференцируя при решении задачи № 44 (см. стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):
Подставляя все эти величины в формулу (72), найдем
Ответ. Нормальное ускорение равно rπ2.
Чтобы преобразовать формулу (72) для случая, когда движение точки задано в естественной форме, припомним из курса высшей математики выражение кривизны плоской кривой, представленной в параметрической форме уравнениями (58′) и (58″),
Если параметр t означает время, то эту геометрическую формулу можно переписать в обозначениях кинематики:
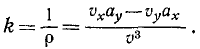
Сравнивая равенства (72) и (73), находим
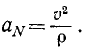
Мы получили положительное значение проекции, следовательно, нормальное ускорение направлено от точки M в положительном направлении оси Mn (см. рис. 91), т. е. в ту сторону от касательной, по которую лежит траектория точки.
Чтобы получить нормальное ускорение в векторном выражении, надо (74) умножить на единичный вектор 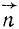
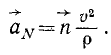
Как уже было сказано, нормальное ускорение не влияет на величину скорости, потому что оно направлено перпендикулярно к скорости. Оно влияет на направление скорости.
Итак, нормальное ускорение—это проекция ускорения точки на нормаль к траектории, направленная в сторону вогнутости, равная квадрату скорости, деленному на радиус кривизны траектории.
Если движение точки прямолинейное, то радиус кривизны траектории (прямой линии) равен бесконечности, а нормальное ускорение равно нулю.
Обратное заключение можно сделать лишь с некоторой оговоркой: если в каждое мгновение данного промежутка времени нормальное ускорение движущейся точки равняется нулю, то точка движется по прямой; если же нормальное ускорение точки не постоянно равно нулю, а только в какое-либо мгновение, то движение точки не а потому
является прямолинейным и равенство 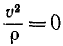
Рис. 93
Величина ускорения точки равна квадратному корню из суммы квадратов касательного и нормального ускорений:
Ускорение при естественном способе задания движения
Если движение точки задано в естественной форме, то проекции ускорения на нормаль и на касательную можно определить по формулам (69) и (74) и по проекциям определить величину полного ускорения точки (см. рис. 91):
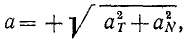
или
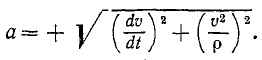
Перед радикалом стоит знак « + », потому что величина ускорения существенно положительна.
Вектор полного ускорения 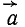
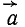
Касательное ускорение направлено по касательной к траектории, а нормальное к центру кривизны траектории, поэтому вектор полного ускорения лежит с той стороны от касательной, с которой расположена траектория точки.
При криволинейном ускоренном движений точки полное ускорение составляет со скоростью острый угол, а при замедленном—тупой.
Вектор ускорения лежит в соприкасающейся плоскости, и проекция ускорения на бинормаль равна нулю:
Разложение ускорения при движении точки по кривой двоякой кривизны. Если кривая не лежит в одной плоскости, то ее называют пространственной кривой, или кривой двоякой кривизны. В каждой точке к кривой можно провести только одну касательную и бесчисленное множество нормалей, расположенных в плоскости, перпендикулярной к касательной и называемой нормальной плоскостью (рис. 94).
рис. 94
Пусть в мгновение t точка занимает на кривой двоякой кривизны положение М. В это мгновение скорость точки направлена по касательной к кривой в точке М. Через эту касательную и через близкую точку M1 (не показанную на чертеже)., в которую движущаяся точка придет в мгновение t + Δt, проведем плоскость и будем стремить Δt к нулю. Тогда точка M1 будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.
Плоскость, проведенную через точку M перпендикулярно к соприкасающейся и к нормальной плоскостям, называют спрямляющей плоскостью.
Нормаль, лежащую в спрямляющей плоскости, называют бинормалью, а нормаль, лежащую в соприкасающейся плоскости,—главной нормалью (главную нормаль плоской кривой обычно называют просто нормалью).
Касательная Mτ главная нормаль Mn и бинормаль Mb пересекаются в точке M под прямыми углами. Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.
Положительные направления на естественных осях примем такими, чтобы трехгранный угол τMnb можно было привести в совпадение с углом xОyz. Касательная Mτ играет роль оси Ох, главная нормаль Mn— оси Oy и бинормаль Mb— оси Oz.
Так как вектор ускорения лежит в соприкасающейся плоскости τМn, а бинормаль Mb перпендикулярна к соприкасающейся плоскости, то проекция ускорения на бинормаль всегда равна нулю (αb = 0), и при проецировании ускорения на три естественные оси мы имеем только две проекции: касательное ускорение и нормальное ускорение.
Таким образом, мы установили, что формулы (69), (69′) и (69″) касательного ускорения, формулы (74) и (74′) нормального ускорения, а также формулы (75) и (75′) полного ускорения, выведенные нами в предположении, что точка движется по плоской траектории, остаются справедливыми для любого движения точки.
Именно потому, что проекция ускорения на бинормаль всегда равна нулю, в формуле (75) величина полного ускорения определяется по двум проекциям, а не по трем, как это имеет место в формуле (66). Приравнивая выражение (66) модуля полного ускорения точки через проекции на неподвижные оси координат его же выражению (75) через проекции на естественные оси, получим для движения точки по любой траектории соотношение
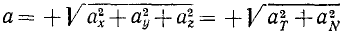
или
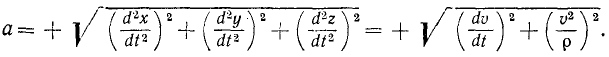
Эти равенства часто бывают полезны при решении задач.
Задача №6
Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями:
Решение. Найдем проекции скорости и ускорения на оси координат:
x=υx=α, χ=ax=0, y = υy = β-gt, y= — g.
Подставляя найденные величины в (68), найдем касательное ускорение
Подставляя те же величины в формулу (72), найдем нормальное ускорение
Нормальное ускорение всегда направлено во внутрь траектории, отрицательный знак получился потому, что в этой задаче естественные оси взяты по левой системе, (ось М,— вправо, ось Mn — вниз), а неподвижные — по правой.
Ответ. 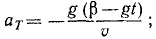
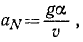
Задача №7
Найти скорость, полное, касательное и нормальное ускорения точки, описывающей фигуру Лиссажу, по уравнениям движения точки, заданным в координатной форме:
х= 3 sin 2t, у = 4 sin 2t.
Решение. Найдем сначала проекции скорости:
υχ = 6 cos 2t, υy = 8 cos 2t.
Затем определим величину полной скорости точки:
Для определения касательного и нормального ускорений определим проекции ускорения на декартовы оси координат, затем найдем полное ускорение и разложим его на касательное и нормальное. Имеем
ax= —12 sin 2t, ay =—16 sin 2t,
Найдем сначала касательное ускорение, для чего продифференцируем по времени полную скорость или воспользуемся формулой (68):
Мы видим, что полное ускорение по величине равно касательному ускорению, т. е. что нормальное ускорение равно нулю. Это возможно только в случае, если траектория — прямая линия. Для проверки можно определить кривизну траектории или найти уравнение траектории. По первому способу имеем
По второму способу найдем 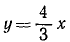
Ответ. υ=10 cos 2t; α = 20 sin 2t; ат= —20sin 2t; αN = 0.
Задача №8
Точка обода колеса, катящегося без скольжения и без буксования по прямолинейному рельсу, движется согласно уравнениям x=r (ct-sin сt), y=r(l — cos ct). Найти нормальное ускорение точки.
Решение. Для решения задачи можно наметить следующий путь: найти проекции скорости, величину полной скорости, проекции ускорения и полное ускорение; затем, продифференцировав по времени величину полной скорости, найти касательное ускорение и, вычитая его геометрически из полного, найти нормальное.
Дифференцируя уравнения движения, найдем
υx= rc (1 —cos ct), υy = rc sin ct.
Далее получаем
Дифференцируя проекции скорости, найдем
ax = rc2 sin ct, ay = rc2 cos ct
полое ускорение
а = rs2
Дифференцируя υ, найдем касательное ускорение:
Вектор aτ перпендикулярен вектору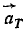
Задачи такого типа быстрее и короче решать с применением формулы (72). По этой формуле непосредственно получаем:
Ответ:
Задача №9
Тяжелое тело, размерами которого можно пренебречь, брошено с большой высоты с горизонтальной скоростью υ0 и движется согласно уравнениям x-υ0t, 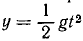
Решение. Определяя из первого уравнения t и подставляя во второе, найдем уравнение траектории:
Траектория—парабола (рис. 95). Дифференцируя уравнения движения по времени, найдем проекции скорости и по ним полную скорость:
В начальное мгновение (t = 0), скорость точки υ = υo, а затем с течением времени величина скорости непрерывно возрастает. Из полученного равенства определим время t, в течение которого тело приобретает скорость у:
Вторично дифференцируя уравнения движения точки, найдем проекции ускорения на оси координат и полное ускорение:
В данном случае тело движется с постоянным по модулю и направлению ускорением, параллельным оси Оу.
Обращаем внимание на то, что, хотя здесь a = const, движение точки не является равнопеременным, так как условием равнопеременного движения является не условие a = const, а условие aт= const. В данном же случае, как мы сейчас увидим, ат непостоянно.
Дифференцируя величину полной скорости по времени или непосредственно по (68), получим касательное ускорение
Подставляя вместо t найденное нами значение, выразим касательное ускорение aт через скорость υ:
Отсюда следует, что в начальное мгновение, когда υ = υ0, aт=0. Затем с увеличением υ величина ат растет и в пределе стремится к полному ускорению g.
Для нахождения нормального ускорения обратимся к (72). Имеем
В начальное мгновение (при t = 0 и υ=v0) aN=g, а затем с увеличением υ аN убывает, стремясь в пределе к нулю.
Ответ. Парабола
Задача №10
Определить радиус кривизны траектории точки в начале движения, если уравнения ее движения имеют вид: x = 2t, y = t2 (t— в cек; х, у— в м).
Решение. Из формулы кривизны (73) имеем
Для получения проекций скорости и ускорения в начальное мгновение продифференцируем уравнения движения и подставим t = 0:
Полную скорость в начальное мгновение определяем по ее проекциям:
Подставляя эти величины в формулу (73), получим ответ.
Ответ. р = 2 м
Задача №11
Через 20 сек после начала движения автомобиль, двигаясь иа закруглении радиуса 400 м, приобрел скорость 108 км/ч. Считая, что величина скорости автомобиля пропорциональна квадрату времени, определить полное ускорение автомобиля в конце 20-й секунды н пройденное за это время расстояние.
Решение. За единицы принимаем метр и секунду. Траектория задана—дорога с закруглением радиуса 400 м, и для решения задачи необходимо определить Уравнение движения автомобиля по траектории. (Применять формулы (71) здесь нельзя, так как при равиоперемениом движении величина скорости пропорциональна времени, а в данной задаче она пропорциональна квадрату времени.)
В условии дано
υ=bt2.
Найдем коэффициент пропорциональности
Выражая скорость по (53) и разделяя переменные, получим
откуда, интегрируя, получаем
Постоянную C определим из начальных данных: в начальное мгновение (t = 0) автомобиль не прошел еще никакого расстояния, а потому C = 0. Дважды дифференцируя по времени полученное уравнение, найдем касательное ускорение
или в конце 20-й секунды
αт=3 м/ceκ2.
Скорость в конце 20-й секунды была 30 м/сек, и по (74)
Полное ускорение в конце 20-й секунды было
Чтобы определить расстояние, пройденное автомобилем за 20 сек, положим в уравнении движения t = 20 сек:
Ответ. а = 3,75 м/сек2, s = 200 м.
- Основные законы динамики
- Колебания материальной точки
- Количество движения
- Момент количества движения
- Приведение системы сил к данной точке
- Система сил на плоскости
- Естественный и векторный способы определения движения точки
- Координатный способ определения движения точки
Содержание:
- Кинематика — основные понятия и определения
- Кинематика точки
- Способы задавания движения точки
- Векторный способ
- Координатный способ
- Натуральный способ
- Связь между различными способами задавания движения точки
- Скорость движения точки
- Определение скорости точки в случае задавания ее движения векторным способом
- Определение скорости точки в случае задавания ее движения координатным способом
- Скорость движения точки в декартовых координатах
- Скорость движения точки в полярных координатах
- Скорость точки с натурального способа задания ее движения
- Годограф скорости точки
- Ускорение движения точки
- Ускорение точки с векторного способа задания ее движения
- Ускорение точки при задании ее движения координатным способом
- Ускорение точки с натурального способа задавания ее движения
- Отдельные случаи движения точки
- Примеры на определение кинематических характеристик движения точки
- Задачи по кинематике с решениями и примерами
- Кинематика точки и её задачи
- Порядок решения задач по кинематике точки
- Примеры решения задач по кинематике точки с решением
- Задания темы К1
- К1.6. Пример решения задания темы К1
- Кинематика — полная лекция с формулами и теорией с примерами
- Кинематика точки
- Траектория и уравнения движения точки
- Координатный способ описания движения точки
- Определение траектории точки при координатном способе описания ее движения
- Определение скорости и ускорения точки при координатном способе описания ее движения
- Порядок решения задач по кинематике точки
- Естественный способ описания движения точки
- Определение скорости и ускорения точки при естественном способе описания ее движения
- Краткие исторические сведенья про развитие кинематики
- Введение в кинематику
- Три способа задания движения точки
- Векторный способ
- Координатный способ
- Натуральный способ
- Скорость движения точки
- Скорость точки в прямоугольной декартовой системе координат
- Скорость точки в полярных координатах
- Скорость точки при натуральном способе заданный движения
- Секторная скорость
- Ускорение точки
- Определение ускорения в прямоугольной декартовой системе координат
- Ускорение точки в полярных координатах
- Ускорение точки при натуральном способе задания движения
- Отдельные случаи движения точки
- Криволинейные координаты. Коэффициенты Ламе
- Скорость и ускорение точки в криволинейных координатах
- Основные понятия кинематики
- Кинематика материальной точки
- Способы задания движения материальной точки
- Векторный способ задания движения материальной точки
- Траектория движения точки
- Скорость движения точки
- Ускорение движения точки
- Координатный способ задания движения материальной точки
- Траектория движения точки
- Скорость движения точки
- Ускорение движения точки
Кинематика — это раздел механики, изучающий математическое описание движения идеализированных тел, без рассмотрения причин движения. Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Кинематика — основные понятия и определения
Кинематикой называется раздел теоретической механики, в котором изучается механическое движение материальных объектов (точек и тел) без связи с причинами, которые вызывают это движение (не учитывается масса подвижного тела и силы, которые вызывают его движение).
Итак, в кинематике изучается механическое движение с геометрической точки зрения. Название «кинематика» происходит от греческого слова «кинема», что означает движение.
Под механическим движением понимается изменение положения одного твердого тела с течением времени по отношению к любому другому телу, которая происходит в пространстве. Это означает, что при изучении движения тела или точки мы должны указать, в отношении которого другого тела рассматриваем движение, то есть связать с последним систему отсчета и считать ее условно неподвижной. Выбор системы отсчета в кинематике произвольный и определяется целью исследования.
Движение одних тел относительно других происходит в пространстве и времени. Пространство в классической механике является абсолютным: оно везде непрерывное, однородное и изотропное , то есть свойства пространства в различных его точках одинаковы, а в каждой точке — одинаковые во всех направлениях.
Геометрические свойства пространства определяются системой аксиом и теорем Евклида. Пространство рассматривается трехмерным, в нем существует понятие о расстоянии между двумя точками или длины отрезка прямой. За единицу длины в системе СІ принято метр (м). Эталон метра был изготовлен в 1795 французским механиком Борда и сохраняется в Севре близ Парижа. Одна из копий международного стандарта метра находится в Палате мер в Москве.
Время в классической механике считается универсальным, то есть одинаковым в любых системах отсчета и независимым от движения одних систем отсчета относительно других. Время является скалярной непрерывно переменной величиной. За единицу времени принимается секунда (с), которая равна примерно 1/86 400 части средней земных суток (земные сутки — это период обращения Земли вокруг собственной оси и равна 24 ч.). При измерении времени в кинематике различают такие понятия, как начальный момент времени, промежуток времени, момент времени. Отсчет времени ведется от некоторого начального момента времени, выбор которого в каждой задачи оговаривается. Время,
проходит между двумя физическими явлениями, называется промежутком времени.
Граница между двумя смежными промежутками времени называется моментом времени.
Понятие об абсолютном пространстве и абсолютное (универсальное) время введено в науку основоположником классической механики И. Ньютоном в знаменитом труде «Математические начала натуральной философии» (1687). Согласно ньютоновской теории пространство и время существуют объективно, независимо друг от друга и не зависят от свойств движущейся материи.
В начале ХХ в. появляется релятивистская механика, основанная на теории относительности. Теория относительности развита в научных трудах Дж. К. Максвелла (1831-1879), Х. А. Лоренца (1853-1928), А. Пуанкаре (1854-1912) и А. Эйнштейна (1879-1955). Принципы теории относительности корне меняют понятие о пространстве и времени. Абстрактному пространству противопоставляется физическое пространство, в котором геометрические свойства пространства и свойства времени сочетаются со свойствами движущейся материи. Время не является универсальным, а имеет «местное» значение. Универсальной постоянной величиной для всех систем является скорость света. Однако
релятивистская механика не исключает классическую механику, а лишь указывает на ее ограниченность и несправедливость ее законов там, где скорость движения тела соизмерима со скоростью света.
Итак, евклидово пространство и универсальное время, принятые в классической механике, лишь приближенно отражают реальные свойства пространства и времени. Однако, как показывает опыт, для тел, скорости движения которых незначительны по сравнению со скоростью света, это приближение дает вполне достаточную для практики точность.
В кинематике используются понятия материальной точки, системы материальных точек, абсолютно твердого тела, которые были введены в статике. Понятие материальной точки и геометрической точки в кинематике совпадают, поскольку масса точки не учитывается. Поэтому в дальнейшем будем употреблять термин «точка». Кроме этих понятий, в кинематике следует различать между собой такие понятия, как перемещение и движение.
Перемещением точки или тела называется переход его в пространстве с одного положения в другое произвольным способом за определенный промежуток времени.
Перемещение полностью определяется начальным и конечным положением точки или тела и промежутком времени. Движением называется переход точки или тела из одного положения в другое определенным способом и в определенной зависимостю от времени. Это означает, что любому положению точки или тела в пространстве соответствует определенный момент времени. Эта связь между положением точки или тела в пространстве и времени определяется законом движения. Если можно определить положение точки или тела в пространстве в любой момент времени, то считается известным закон ее движения.
Основная задача кинематики заключается в том, чтобы, зная закон движения точки или тела, установить основные кинематические характеристики движения. К основным кинематическим характеристикам движения относятся траектории, скорости и ускорения точек тела, а также угловая скорость и угловое ускорение тела. Кинематика делится на кинематику точки и кинематику твердого тела. Изучение кинематики начинается с изучение движения отдельной точки, а затем изучают движение твердого тела.
Кинематика точки
Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.
Способы задавания движения точки
Задать движение точки — это значит установить совокупность таких параметров, с помощью которых можно однозначно определить положение точки в пространстве в любой момент времени.
Движение точки в пространстве можно задать тремя способами: векторным, координатным и натуральным.
Векторный способ
Положение точки в пространстве в каждый момент времени можно определить с помощью
радиус-вектора 
Каждому моменту времени t, а следовательно, и положению точки М, соответствует определенное значение радиусавектора 
функцией времени
Уравнение (2.1) называют векторным уравнением движения точки. Оно одновременно является и уравнением траектории точки М.
Траекторией движения точки называется геометрическое место последовательных
положений подвижной точки в пространстве. В данном случае это будет геометрическое место концов радиус-вектора 


Векторный способ задавания движения точки преимущественно применяется при теоретических исследованиях.
Координатный способ
Положение точки по отношению к любой системе отсчета полностью определяется ее координатами. Если задать координаты точки как известные функции времени в некоторой системе отсчета, то это дает определить ее положение в пространстве в произвольный момент времени. Таким образом задания движения точки называется координатным.
Рассмотрим движение точки в декартовой системе координат. Положение точки М в пространстве будет известным, если задано значение трех ее декартовых координат 

Уравнение (2.2) являются уравнениями движения точки в координатной форме и
одновременно параметрическими уравнениями траектории точки. Исключив параметр t из этих уравнений, получим уравнение траектории движения точки в координатной форме.
Если точка движется в плоскости, то, приняв ее за плоскость
В случае прямолинейного движения точки положения ее определяется одним уравнением
при условии, что ось 
Если движение точки происходит в плоскости, то иногда целесообразно использовать полярную систему координат (рис. 2.3). Для этого из телом отсчета свяжем полярную ось 

Полярный угол φ считается положительным, если его отчисляют от полярной оси 
Координатный способ определения движения точки применяют как во время теоретических исследований, так и при решении конкретных задач.
Кроме декартовой и полярной систем координат в механике часто применяют еще и такие системы, как цилиндрическая и сферическая.
Натуральный способ
Пусть точка М описывает в пространстве некоторую кривую АВ (рис. 2.4), которая является траекторией точки. Для того, чтобы определить положение точки М на траектории в произвольный момент времени, выберем на ней начало отсчета О и установим положительный и отрицательный направления движения.
Тогда положение точки М на траектории однозначно определится криволинейной координатой 
Каждому моменту времени соответствует определенное положение точки М на траектории, а следовательно, и определенное значение дуговой координаты, то есть,
дуговая координата является функцией времени
Уравнение (2.7) выражает закон движения точки М по траектории, но не определяет положение ее в пространстве.
Итак, по натуральному способу определения движения точки положения ее в пространстве задается совокупностью следующих параметров: траекторией точки, началом отсчета дуговой координаты, направлением положительного отсчета дуговой координаты, законом движения по траектории в виде (2.7).
Не следует утотожнюваты значение дуговой координаты с пройденным точкой путем. На рис. 2.5, а точка в начальный момент времени 

Значение дуговой координаты 

Заметим, что функции, которые входят в равенства (2.1), (2.2), (2.5), (2.7), по самой природе движения должны быть однозначными, непрерывными и хотя бы дважды дифференцированными.
Связь между различными способами задавания движения точки
Между различными способами задания движения точки существует взаимосвязь. Установим его между векторным и координатным способами.
Пусть задано векторное уравнение движения точки (2.1), где радиус-вектор 
Тогда координаты точки М равны проекциям радиус-вектора 
Если же, наоборот, задано уравнение (2.2), а нужно составить векторное уравнение, то, введя орты координатных осей
Покажем, что существует связь между координатным и натуральным способами определения движения точки. Пусть движение точки задано уравнениями (2.2), которые одновременно являются и параметрическими уравнениями траектории. Исключив из них параметр t, получим уравнение траектории. Решая, например, последнее уравнение
системы (2.2) по t, получим 
Как известно из аналитической геометрии, линии в пространстве отвечают два уравнения с тремя координатами, то есть уравнение (2.10) являются уравнениями траектории точки в декартовых координатах.
Установим закон движения по траектории. Пусть за промежуток времени dt произошел прирост дуговой координаты dS, равный дифференциала длины дуги S. По известным формулам дифференциальной геометрии элемент дуги dS исчисляется


Тогда
Замечания. В механике производная по времени обозначается точкой над функцией. Например,
Интегрируя выражение (2.11) в промежутке от 
Знак «плюс» или «минус» перед интегралом ставится в зависимости от направления движения точки: если точка движется в сторону выбранного положительного направления отсчета дуговой координаты, то ставится знак «плюс», в противном случае — «минус». Начало отсчета дуговой координаты совпадает с начальным положением точки на траектории.
Скорость движения точки
Одной из основных кинематических характеристик движения точки является ее скорость. Скоростью точки называется векторная величина, которая характеризует в каждый момент времени изменение положения и направление движения точки в данной системе отсчета.
Определим скорость точки при различных способах задания ее движения.
Определение скорости точки в случае задавания ее движения векторным способом
Пусть в момент времени t положение точки М определяется радиусомвектором 





Из рис. 2.7 видно, что 



Введем понятие о средней скорости точки за некоторый промежуток времени. Отношение вектора перемещения 

Вектор 





Итак, вектор скорости точки в заданный момент времени равен первой производной по времени от радиус-вектора точки
Поскольку при 




Единицей измерения скорости в системе СІ является метр в секунду (м / с).
Определение скорости точки в случае задавания ее движения координатным способом
При координатном способе задания движения точки модуль и направление скорости находят через проекции ее на оси координат, согласно следующей теореме: проекции скорости точки на неподвижные оси равны первым производным от соответствующих координат точки по времени.
Скорость движения точки в декартовых координатах
Рассмотрим определение скорости точки в случае задавания ее движения координатным
способом в декартовой системе координат.
Пусть движение точки М задано в системе координат 
Учитывая, что орты 

С другой стороны, разложив вектор скорости 
где 

Сравнивая формулы (2.16) и (2.17), находим
Итак, проекции вектора скорости точки на оси декартовой системы координат равны первым производным по времени от соответствующих координат точки.
Как видно из рис. 2.8, модуль вектора скорости и его направляющие косинусы определяются по формулам
Формулы (2.18) и (2.19) аналитически определяют вектор скорости точки в декартовой системе координат.
Скорость движения точки в полярных координатах
Рассмотрим способ определения скорости точки, когда ее движение задано в полярных координатах уравнениями (2.5). Для этого введем единичные вектора: 
направлен по радиусу ОМ от точки О до точки М, и 


часовой стрелки (рис. 2.9).
Тогда 
Выразим векторы 



Найдем производные по времени от полученных выражений для 
Тогда формула (2.20) принимает вид
Выражение (2.22) является расписанием вектора скорости точки на две составляющие,
которые называются соответственно радиальной 

где
Проекции радиальной и трансверсальной скоростей на оси полярной системы координат, положительные направления которых совпадают с направлениями единичных векторов
и 
В зависимости от знаков производных 

где 

Скорость точки с натурального способа задания ее движения
Определим скорость движения точки, считая, что движение задано натуральным способом, то есть известные траектория движения, начало и направление отсчета дуговой координаты и уравнения движения точки по траектории 

Поскольку дуговая координата является функцией времени, то радиус-вектор 
сложной функцией времени
Если за промежуток времени 






вектор скорости 
Рассмотрим векторную величину
Как известно из дифференциальной геометрии, предел отношения длины дуги до хорды, что стягивает ее, по модулю равен единице, а предельное положение хорды 
где 
Действительно, при 

координаты (рис. 2.10, а), а при 



Учитывая вышеизложенное, формулу (2.27) можно записать в виде
Модуль (величина) скорости
Формула (2.27) определяет вектор скорости точки с натурального способа задания ее движения. Умножив скалярно почленно это равенство на вектор 
или, поскольку
Итак, производная 
траектории и формулу (2.27) можно записать в виде
Алгебраическое значение скорости точки — это проекция вектора скорости на касательную ось. Она определяется формулой (2.30).
Если 




Годограф скорости точки
Пусть точка М движется по криволинейной траектории. скорость точки при этом будет меняться как по величине, так и по направлению. На рис. 2.11, а показан ряд положений точки М на траектории и ее скорости 

Выберем произвольную неподвижную точку 
параллельно самим себе векторы скоростей (рис. 2.11, б).Поскольку вектор 
Итак, годографом скорости называется геометрическое место концов векторов скорости подвижной точки, отложенных от произвольной точки пространства.
Найдем уравнение годографа скорости. Для этого через неподвижную точку 

Радиусом-вектором произвольной точки N на годограф будет вектор скорости 

Параметрические уравнения годографа скорости точки запишем в виде:
Ускорение движения точки
Рассмотрим ускорение точки, которое также является одной из основных кинематических характеристик ее движения. Ускорением точки называется векторная величина, характеризующая изменение вектора скорости точки по величине и направлению с течением времени. Найдем ускорение точки при различных способах задания ее движения.
Ускорение точки с векторного способа задания ее движения
Пусть подвижная точка М в момент времени t имеет скорость 


Найдем прирост 




Отношение прироста вектора скорости 

Формула (2.31) указывает на то, что вектор 


когда соответствующий промежуток времени 
Зависимость (2.32) с учетом (2.15) запишем в виде
Итак, вектор ускорения точки в заданный момент времени равна первой производной по времени от вектора скорости точки, или второй производной по времени от радиус-вектора этой точки.
Установим направление вектора ускорения. Для этого построим годограф вектора скорости на рис. 2.13, б. Вектор среднего ускорения 





Стоит заметить, что приведенный выше способ нахождения направления ускорения представляет лишь теоретический интерес. во время практического решения задач пользуются удобными методами нахождения направления ускорения, которые будут приведены ниже. Единицей измерения ускорения в системе СІ является метр в секунду в
квадрате
Ускорение точки при задании ее движения координатным способом
1. Ускорение движения точки в декартовых координатах
Определим ускорение точки в декартовой системе координат.
Пусть движение точки М задано в системе координат

На основании (2.33) и, учитывая, что векторы 
Разложим вектор 
где 
Сравнивая (2.34) и (2.35), получим
Учитывая (2.18), формулы (2.36) можно записать в виде
Итак, проекции вектора ускорения на декартовы оси координат равны вторым производным по времени от соответствующих координат точки или первым производным по времени от проекций скорости на соответствующие оси.
Модуль вектора ускорения и его направляющие косинусы определяются по формулам
2. Ускорение движения точки в полярных координатах
Пусть движение точки М в плоскости задано в полярных координатах 
Но согласно (2.21)
Учтя выражения этих производных в формуле (2.39) и сведя подобные слагаемые, получим выражение для ускорения точки
Из формулы (2.40) видно, что проекции ускорения на радиальный и трансверсально направления соответственно равны
Поскольку 

Для определения направления вектора ускорения найдем угол γ, образованный вектором 
Ускорение точки с натурального способа задавания ее движения
Прежде чем перейти к определению ускорения точки с натурального способа задания ее движения, напомним некоторые положения дифференциальной геометрии, касающихся теории кривых в трехмерном пространстве.
1. Натуральная система координат
На пространственной кривой АВ, которая является траекторией движения точки, рассмотрим два близкие положение точки 

касательные к кривой, орты которых обозначим соответственно 






ристической плоскостью.
Через точку М перпендикулярно к касательной 

Линия пересечения ристической и нормальной плоскости называется главной нормалью кривой. Плоскость, проведенная через точку М перпендикулярно к главной нормали, называется спрямною плоскостью (плоскость ІІІ на рис. 2.15). Линия пересечения спрямнои и нормальной плоскости называется бинормаллю кривой. Соприкасающаяся, нормальная и спрямна плоскости образуют натуральный трехгранник.
Итак, в каждой точке кривой можно провести три взаимно перпендикулярные направления и принять их за координатные оси: касательную, направленную в сторону увеличения дуговой координаты; главную нормаль, направленную в сторону вогнутости кривой, и бинормаль, направленную перпендикулярно касательной и главной нормали так, чтобы образовывать с ними правую систему осей. Орты этих осей обозначаются соответственно 
2. Кривизна кривой
В п. 2.3.3 было показано, что орт 
Модуль орта 



Проследим, чему равно отношение прироста орта 



Проведем орты 




Разделив 








Определим модуль вектора кривизны 



Угол 




Тогда
С дифференциальной геометрии известно, что предел отношения угла смежности 



Установим направление вектора кривизны 




При приближении точки 

Поскольку вектор кривизны лежит в соприкасающихся плоскости и перпендикулярно к орту 

3. Определение ускорения движения точки. Касательное и нормальное ускорение
Определим ускорение точки с натурального способа задания ее движения. Используя формулы (2.33) и (2.28), получим
Определим, какой смысл имеет вектор 


Поэтому
Учитывая формулы (2.47) и (2.45), выражение (2.46) запишем
Из формулы (2.48) следует, что ускорение состоит из двух векторов. Первое слагаемое 

Второе слагаемое 

Таким образом, полное ускорение точки равна векторной сумме касательного и
нормального ускоренного:
Выясним, который кинематический смысл имеют две составляющие ускорения. Алгебраическое значение касательного ускорения согласно (2.49) и (2.30) можно записать в виде
Как видно из формулы (2.52), касательное ускорение характеризует изменение скорости точки по величине и равна второй производной по времени от дуговой координаты или первой производной по времени от алгебраической величины скорости точки.
Направление касательного ускорения 
Если знак производной совпадает со знаком алгебраической величины скорости
то вектор 





Скалярный множитель в формуле (2.50) есть всегда положительным, поэтому величина (модуль) нормального ускорения равен
Вектор 
Поскольку векторы 

Вектор полного ускорения 


Замечания. Вектор полного ускорения 
Если движение точки задано координатным способом, а необходимо определить ее касательное и нормальное ускорения, то сначала по формулам (2.19) и (2.38) определяют модули скорости и ускорения точки
Формуле (2.52) можно придать другой вид:
или
где знак «плюс» в ответе избирается, если 
Нормальное ускорение точки определяется по формуле (2.54)
Радиус кривизны траектории находим из формулы (2.53):
Зависимости для кинематических характеристик движения точки при различных
способах задания движения сведены в табл. 2.1.
Таблица 2.1
Кинематические характеристики движения точки
Отдельные случаи движения точки
Проследим, как зависит характер движения точки от значений касательного и нормального ускорение.
1. Если во время движения точки в течение некоторого промежутка времени ее нормальное и касательное ускорение равны нулю




2. Если в течение некоторого промежутка времени касательное ускорение точки равно нулю


Найдем уравнение равномерного движения точки. Пусть в начальный момент времени точка находилась на расстоянии 
Интегрируя это уравнение в соответствующих пределах, получим:
Уравнением равномерного движения точки по траектории будет
Замечания. если 
точки неравномерно, а в данный момент времени скорость ее достигает экстремального значения (если 
3. Если во время движения точки в течение некоторого промежутка времени нормальное ускорение точки равно нулю 



Ускорение точки в этом случае 
и 


Если же направления векторов 



разные, то движение точки будет замедленным (рис. 2.18, б). Если 

меняет направление движения на противоположное
4. Если в течение некоторого промежутка времени касательное и нормальное ускорение не равно нулю 

5. Если во время движения точки по траектории касательное и нормальное ускорение не равно нулю 

Найдем уравнение равномерного движения точки по траектории, считая, что в начальный момент времени 

Согласно формуле (2.52)
Разделим переменные величины и проинтегрируем уравнение в пределах, что соответствуют начальном и бегущей положениям точки:
Выражение (2.58) является законом изменения скорости по ровносменного движения точки.
Поскольку 
Проинтегрируем последнее выражение и получим:
откуда
Зависимость (2.59) является уравнением ровносменного движения точки по траектории.
При

Отдельные случаи движения точки в зависимости от ее кинематических параметров
приведены в табл. 2.2.
Таблица 2.2
Отдельные случаи движения материальной точки
Примеры на определение кинематических характеристик движения точки
Задача 2.1. В механизме эллипсограф ползуны А и В соединены между собой линейкой АВ и могут двигаться по двум взаимно-перпендикулярных направлениях (рис. 2.19).
Механизм приводится в движение кривошипом ОС, который вращается с постоянной угловой скоростью ω вокруг точки О.
Найти уравнение траектории, скорость, уравнение годографа скорости и ускорения точки М линейки АВ, если:
Решение. Как было показано выше, для нахождения кинематических характеристик движения точки необходимо иметь уравнение ее движения, заданные одним из способов. В данной задачи уравнения движения точки М непосредственно не заданы, а потому
решения ее необходимо начинать с нахождения этих уравнений.
Составим уравнения движения точки в декартовой системе координат. для этого оси 



Из рис. 2.20 видно, что
Согласно условию задачи 
Для определения уравнения траектории точки М исключим время t из уравнений движения
(Здесь и далее индекс М не пишем)
Обе части этих равенств поднимем к квадрату и почленно добавим.
Получим
Итак, траектории точки М будет эллипс с полуосями а, b.
Для определения скорости точки М в произвольный момент времени используем формулы (2.18) и (2.19). тогда
Направление вектора 
Найдем уравнение годографа скорости по формулам
Исключим из этих уравнений параметр t:
Годографом скорости является эллипс с полуосями 
Ускорение точки М найдем за его проекциями на оси координат по формулам (2.37), (2.38)
Итак, ускорение точки пропорционально ее расстоянию от начала координат OM = r.
Направление вектора ускорения определим за направляющими косинусами
Заметим, что в данной задаче величины 





Задача 2.2. Движение точки задано уравнениями 
Решение. Заданные уравнения движения точки являются параметрическими уравнениями
траектории. Исключим из них время t и получим
Поскольку время 
Итак, траекторией точки является правая ветвь параболы (рис. 2.21). Покажем на ней положение точки М. При 
Модуль скорости точки равен
Ускорение точки определим аналогично по проекциями на оси координат
Величина касательного ускорения по формуле (2.52) равна
Найдем нормальное ускорение точки по формуле
Радиус кривизны траектории в данной точке М по формуле (2.53) равна
Векторы 
Задача 2.3. Точка движется по окружности радиуса R = 20 см по закону
Решение. Как видно из условия задачи, движение точки задано натуральным способом. Алгебраические величины скорости и касательного ускорения равны
При 

Таким образом, полное ускорение точки в данный момент времени равна ее нормальном ускорению
Задача 2.4. Самолет приземляется со скоростью 108 км / ч. Проехав 100 м, он остановился. Считая движение самолета прямолинейным и ровнозамедленным определить его ускорения.
Решение. Поскольку движение самолета ровнозамедленное то касательное ускорение
В данной задачи
Время движения самолета к остановке и пройденный им путь определим, принимая конечные условия движения: при
Тогда
Откуда
Поскольку 
Задачи по кинематике с решениями и примерами
В данной части кроме минимума теоретических знаний, какими должен овладеть студент по кинематике, приводятся примеры решения различных задач, исходные данные в
индивидуального расчетного-графического задания и образец его выполнения.
Задачи расчетно-графического задания охватывают материал следующих тем кинематики:
- — кинематика точки (тема КИ);
- — поступательное и вращательное движения тела (тема К2);
- — плоское движение тела (тема К3);
- — сложное движение точки (тема К4).
Задачи 1,3 и 4 объединены в общие выходные данными.
Графические построения к заданию по кинематике выполняются на листе бумаги формата А3.
Вариант расчетно-графического задания определяется двумя цифрами, которые представляют собой две последние цифры номера зачетной книжки или задаются преподавателем.
Для тем К1, К3 и К4 первая цифра шифра определяет номер варианта в таблице К1, а вторая — в таблице К2. Для темы К2 первая цифра шифра определяет номер рисунка (рис.
К2.2), а вторая — вариант в таблице К3.
Кинематика точки и её задачи
Краткие сведения из теории:
Кинематика — раздел теоретической механики, в котором изучаются геометрические свойства механического движения материальных тел без учета условий и причин, которые вызывают или меняют это движение, то есть без учета масс тел и сил которые действуют на эти тела.
Основной задачей кинематики точки является обозначение ее движения и определения основных характеристик этого движения: траектории, пройденного пути, перемещения, скорости и ускорение в любой момент времени относительно выбранной
системы отсчета.
При координатном способе определения движения точки его кинематические уравнения выражены зависимостью координат точки от времени. В прямоугольной (декартовой) системе координат 
Когда точка движется в плоскости, например, 
Траекторией точки называется линия, которая описывается подвижной точкой в пространстве. Траектория точки выражается уравнением в виде зависимости между ее координатами:
При координатном способе определения движения скорость точки определяется через ее проекции на координатные оси:
а величина (модуль) скорости соответственно равна:
Вектор скорости направлен по касательной к траектории в сторону движения точки. Единицей измерения скорости в системе СИ есть метр в секунду:
Ускорение точки — векторная величина, которая характеризует быстроту изменения скорости со временем.
При координатном способе определения движения точки проекции ускорения точки на координатные оси равны:
Величина (модуль) ускорения вычисляется по формулой:
Единицей измерения ускорения в системе СИ является метр в секунду в квадрате:
Если известна траектория точки и выбрана естественная система координат 




центростремительную) по оси
Тангенциальное ускорение 
При этом, если величины 
и 



Если дифференцировать по времени выражение скорости точки при ее движении в плоскости 
Нормальное 
где 
Полное же ускорение через нормальную и тангенциальную составляющую соответственно равно:
Порядок решения задач по кинематике точки
При решении задач на определение скорости и ускорение точки нужно придерживаться следующего порядка:
1. Выбрать систему координат.
2. Составить уравнение движения точки в выбранной системе координат.
3. Дифференцируя уравнение движения точки определить проекции вектора скорости на оси координат, его величину и направление.
4. Дифференцируя уравнение проекции скорости, определить проекции вектора ускорения на оси координат, его величину и направление.
Примеры решения задач по кинематике точки с решением
Задача 1
Движение точки на плоскости определяется уравнениями:
Определить уравнение траектории и направление движения точки.
Решение. Уравнение траектории указано в параметрической форме, координаты 


Чтобы получить уравнение траектории в координатной форме, то есть в виде зависимости 
Возведем квадрат левые и правые части уравнений движения:
или
Добавим эти уравнения:
Поскольку
Уравнением траектории точки является эллипс с центром в начале системы координат, большая полуось которого равняется 5-ти единицам длины (по оси 

В начальный момент времени 

В начальный момент движения (при росте 


Таким образом, точка будет двигаться за ходом часовой стрелки.
Ответ:
а) уравнение траектории
б) точка движется по ходу часовой стрелки.
Задача 2
В механизме (рис.1) тело ОА (кривошип) вращается вокруг неподвижного шарнира О, а тело В(ползун) движется обратно-поступательно по оси 
Определить уравнение движения и траекторию средней
точки М шатуна и уравнения движения ползуна В, если в начальный момент ползун находился в крайнем правом положении; кривошип ОА вращается с постоянной угловой скоростью
Решение. Для определения траектории точки М изобразим механизм в произвольном положении и составим уравнение ее движения в координатной форме.
Из рис. 1 видно, что:
Поскольку треугольник ОАВ равнобедренный (ОА = АВ), углы АВС и АОС равны между собой и равны
Из треугольника ОАС найдем расстояние OC:

Тогда:
Если учесть числовые данные, то уравнения движения точки М приобретут вид:
Для нахождения траектории точки М возведем уравнение движения к квадрату и добавим:
Учитывая, что 
Таким образом, траекторией точки будет эллипс, одна полуось которого, по оси 

Определим координаты точки В:
Таким образом, уравнение движения ползуна В будет иметь вид:
Ответ:
Задача 3
Точка движется по кругу радиусом R =4 м. Путь в метрах, который проходит точка по траектории, в любой момент времени определяется уравнением:
Определить величину ускорения точки и угол 
равняется 6
Решение. Изобразим траекторию с точкой М в произвольном положении (рис.1).
Скорость 
— к центру круга, а касательное 
Угол 


Найдем величину нормального ускорения:
Функциональные зависимости для скорости и касательного ускорения найдем по уравнению движения точки:
Поскольку для вычисления ускорения надо знать время, когда скорость будет равняться 6 м/с, то из первого уравнения получим:
Величина касательного ускорения:
Тогда:
Полное ускорение точки:
Ответ:
Задания темы К1
Кинематические уравнения движения точки А тела, что движется в плоскости 
Коэффициенты 




Определить: уравнение траектории, скорость, ускорение точки А и радиус кривизны траектории точки в момент времени 
координат 

скорость и ускорение, касательное и нормальное ускорение.
К1.6. Пример решения задания темы К1
Рассмотрим пример при таких исходных данных и коэффициентах:
1. Определение кинематических уровней движения точки А
Подставим значение соответствующих коэффициентов в уравнение (К1.12), тогда:
После вычислений получим:
Полученные выражения и являются искомыми кинематическими уравнениями движения точки А.
2. Определение уравнения траектории точки А
Для определения уравнения траектории удалим из уравнений (1) параметр 

Полученное выражение является уравнением траектории точки А и
представляет собой эллипс с полуосями, по оси 
оси 
Для определения положения точки А на траектории в момент времени 

3. Определение скорости точки А
Поскольку проекция скорости на ось равна производной по времени от соответствующей координаты (К1.4), то:
В момент времени 
Отрицательное значение проекции 


4. Определение ускорения точки А и радиуса кривизны траектории.
Воспользовавшись выражениями (2) определим проекции ускорения точки А на оси 
В момент времени 
Полное ускорение в момент времени
Знаки минус перед значениями проекций 

и 

Из формул (К1.9, К1.11) определим величины тангенциального и нормального ускорения:
По известной скорости 

5. Графические построения
По результатам расчетов строится чертеж (черта К1.2).
Поскольку полученные размеры измеряются в метрах, а на чертеже откладываются в миллиметрах, то постройки выполняются в определенном масштабе (это же касается и отрезков, которые изображают на чертежах векторы скоростей и ускорений). Для этого сначала необходимо определить масштабные коэффициенты длин 
и ускорений
Масштабным коэффициентом 
Отрезок, изображающий определенную величину на чертеже, подбирают произвольно исходя из следующих соображений:
- чертеж должен иметь определенные размеры (не быть очень большим, или очень маленьким);
- по возможности величина масштабного коэффициента должна иметь одну значимую цифру.
По определенными масштабными коэффициентами надо перечислить действительные величины найденных параметров в отрезки, которые будут изображать эти величины на чертеже, и только после этого выполнять построения на чертеже.
Выберем масштабный коэффициент длин 
Выберем любой из этих размеров, например 


При этом отрезки, которые будут изображать на чертеже линейные величины равны:
Выберем масштабный коэффициент скоростей
При решении задачи были найдены скорости:
Выберем любую из этих скоростей, например 


При этом отрезки, которые будут изображать на чертеже составляющие скорости будут равняться:
Выберем масштабный коэффициент ускорений
При решении задачи были найдены ускорения:
Выберем любое из этих ускорений, например



При этом отрезки, которые будут изображать на чертеже составляющие ускорения будут равны:
На чертежах (рис К1.2):
1. С произвольной точки О под прямым углом одна к второй проводим координатные оси 
2. Строим траекторию точки по известным полуосям эллипса 


3. Показываем точку А в момент времени 

4. По известным отрезкам 



5. Определяем скорость точки 
6. По известным отрезкам 



соответствующей оси);
7. Определяем ускорение точки 
8. Изображаем составляющие ускорения 

9. По известным направлением 


Следует помнить , что вектор скорости направлен по касательной траектории точки, а вектор ускорения — в сторону кривизны траектории.
Кинематика — полная лекция с формулами и теорией с примерами
Кинематикой называется раздел теоретической механики, в котором изучается механическое движение тел с геометрической точки зрения, то есть без учета их масс и сил, что на них действуют.
Движение тел в кинематике рассматривают по отношению к некоторой системе координат, которая связана с другим телом, например, с Землей.
Основная задача кинематики заключается в том, что по уравнениям, которые определяют закон движения данного тела, надо найти все кинематические характеристики движения тела (траектории различных точек, их скорости и ускорения).
Кинематика делится на кинематику точки и кинематику твердого тела.
В первом разделе учебного пособия рассматриваются следующие темы кинематики:
- Кинематика точки.
- Поступательное движение тела.
- Вращательное движение тела вокруг неподвижной оси.
- Плоское движение тела.
- Сложное движение точки.
На изучение этих тем отводится восемь занятий.
Кинематика точки
Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.
Траектория и уравнения движения точки
Описать движение точки – это значит указать правило, по которому в любой момент времени 
Различают три способы описания движения точки: координатный; векторный; естественный.
Координатный способ описания движения точки
Положение точки 

Если точка движется, то эти координаты со временем непрерывно меняются.
Таким образом, для описания движения точки достаточно задать функциональные зависимости вида:
Уравнения (1.1) называются уравнениями движения точки в прямоугольных координатах.
Движение точки в плоскости, например 
Для описания прямолинейного движения точки, например, по оси 
Определение траектории точки при координатном способе описания ее движения
Траекторией называется та совокупность точек, через которые последовательно проходит тело во время движения в данной системе отсчета.
Траектория – одна из основных характеристик, которая дает представление о движении в целом. Первым признаком, по которому выполняется распределение движений на разные виды, является траектория.
Определение траектории является одной из важных частей задач механики.
В зависимости от формы траектории движение относят к прямолинейному или криволинейному движению.
Уравнение движения точки 
Для того, чтобы получить уравнение траектории в обычном виде, надо из уравнений движения исключить время 

которое представляет собой уравнение линии на плоскости 
Если исключить время 
Каждое из уравнений системы (1.5) является уравнением некоторой поверхности, а вместе – уравнением траектории, которая представляет собой линию пересечения этих поверхностей.
Определение скорости и ускорения точки при координатном способе описания ее движения
Скорость точки – векторная величина, которая характеризует изменение положения точки в пространстве с течением времени.
Ускорение точки – векторная величина, которая характеризует изменение вектора скорости с течением времени.
В случае координатного способа описания движения точки по известным зависимостям для координат точки (1.1) сначала определяют проекции вектора скорости на координатные оси:
а затем модуль скорости точки:
Направление вектора скорости 
Проекции вектора ускорения на координатные оси соответственно равны:
Модуль вектора ускорения определяется по формуле:
Направление вектора ускорения 
Порядок решения задач по кинематике точки
Решение задач на определение закона движения точки и уравнения ее траектории выполняется в такой последовательности:
- Выбирается неподвижная система координат, начало которой определяют, исходя из условий задачи.
- По условиям задачи в избранной системе координат составляют уравнение движения точки, то есть находят зависимость координат точки от времени.
- Из составленных уравнений движения точки можно определить ее положение в любой момент времени, установить направление ее движения, найти траекторию и т.д.
Если по условию задачи надо определить скорость и ускорение точки, то лучше придерживаться такой последовательности:
- Выбрать систему координат.
- В выбранной системе координат составить уравнения движения (иногда они заданы в условиях задачи).
- По уравнениям движения точки определить проекции скорости на оси системы координат, величину скорости и ее направление.
- Определить проекции ускорения точки на оси системы координат, величину ускорения и его направление.
Примеры решения задач
Задача №1
Движение точки на плоскости определяется уравнениями:
Определить уравнение траектории и направление движения точки.
Решение. Уравнение траектории задано в параметрической форме, координаты 


Чтобы получить уравнение траектории в координатной форме, то есть в виде зависимости 

Возведем в квадрат левые и правые части уравнений движения:
или
Сложим эти уравнения:
Поскольку 
Уравнением траектории точки является эллипс с центром в начале системы координат, большая полуось которого равна 5-ти единицам длины (по оси 


В начальный момент времени 

В начальный момент движения (при росте 


Ответ: а) уравнение траектории 
Задача №2
В механизме (рис.1.3) тело 







Определить уравнение движения и траекторию средней точки 



Решение. Для определения траектории точки 
С рис. 1.3 видно, что:
Поскольку треугольник 




Из треугольника 

а из треугольника 


Тогда:
Если подставить числовые данные, то уравнения движения точки 
Для нахождения траектории точки 
Учитывая, что 
Таким образом, траекторией точки будет эллипс, одна полуось которого, по оси 

Определим координаты точки 
Таким образом, уравнение движения ползуна 
Ответ.
Задача №3
Движение точки 
где 


Определить траекторию точки, величину и направление скорости и величину и направление ускорения в момент времени
Решение. Для определения траектории точки 
Таким образом, уравнение траектории будет иметь вид:
Траекторией точки 
Проекции вектора скорости на оси координат равны:
Модуль вектора скорости:
Проекции вектора ускорения на оси координат равны:
Модуль вектора ускорения:
Из полученных зависимостей следует, что модули скорости и ускорения не зависят от времени, а их проекции на оси являются функциями времени.
Определим для момента времени 
При 
С учетом найденного угла получим:
На рис.1.4 показана траектория точки, положение точки в момент времени 
Составляющие векторы 

Ответ.
Задача №4
Движение точки задано уравнениями:
где 

Определить уравнение траектории, скорость и ускорение точки, как функцию радиуса-вектора
Решение. Уравнение траектории в координатной форме найдем, исключив время из уравнений движения точки.
Сначала уравнение движения преобразуем в вид:
Возведем записанные уравнения к квадрату и вычтем от первого второе:
Таким образом, уравнение траектории точки будет иметь вид:
Определим проекции вектора скорости на координатные оси:
Поскольку по условию задачи:
то
Тогда:
Определим проекции вектора ускорения на координатные оси:
Учитывая, что 
Ответ.
Задачи, которые рекомендуются для самостоятельной работы: 11.2; 11.5; 12.13 [2].
Естественный способ описания движения точки
Естественный способ описания движения точки заключается в следующем.
- Любым способом (уравнением, графически, указанием) задается траектория точки
(рис.1.5) .
- На траектории выбирается некоторая точка
как начало отсчета дуги и положительное направление вдоль траектории (на рис. 1.5 слева направо).
- Положение точки
на траектории однозначно определяется длиной дуги
, которую берут с соответствующим знаком. При движении точки по траектории каждому моменту времени
соответствует определенное значение
.
Таким образом, для определения положения точки на траектории достаточно задать зависимость:
которая называется естественным уравнением движения.
Естественным способом описания движения точки удобно пользоваться в том случае, когда известна траектория точки.
Определение скорости и ускорения точки при естественном способе описания ее движения
В случае естественного способа описания движения точки по известному уравнению движения (1.12) модуль вектора скорости определяют по формуле:
Направлен вектор скорости по касательной к траектории точки в сторону отсчета координаты 

При определении ускорения с точкой 



Ускорение 


По модулю эти ускорения, соответственно, равны:
где 
Нормальное ускорение всегда направлено к центру кривизны (по направлению оси 



Нормальное ускорение характеризует изменение направления скорости с течением времени.
Если траекторией точки является прямая линия, то есть 

Касательное ускорение характеризует изменение скорости по величине с течением времени.
Если точка движется равномерно 

В случае равномерно ускоренного движения точки 
В приведенных формулах 


Примеры решения задач
Задача №1
Точка движется по окружности радиусом 
где 

Определить величину и направление скорости, касательное и нормальное ускорение точки в момент времени
Решение. Для определения модуля скорости найдем производную от 
В момент времени 
Скорость точки направлена по касательной к окружности в сторону, которая противоположная положительному направлению отсчета дуги 
Определим величину касательного ускорения:
В момент времени 
Вычислим величину нормального ускорения в момент времени 
Ответ.
Задача №2
Точка движется по окружности радиусом 
Определить величину ускорения точки и угол 
Решение. Изобразим траекторию с точкой 



Угол 


Найдем величину нормального ускорения:
Функциональные зависимости для скорости и касательного ускорения найдем по уравнению движения точки:
Поскольку для вычисления касательного ускорения надо знать время, когда скорость будет равна 
Величина касательного ускорения:
Тогда:
Полное ускорение точки:
Ответ.
Задача №3
Уравнение движения пальца шарнира 
где 

Определить скорость, касательное и нормальное ускорение пальца.
Решение. Уравнения для определения касательного и нормального ускорения имеют вид:
Таким образом, для определения 




Для вычисления 
Скорость пальца кривошипа будет равна:
Вычислим величину касательного ускорения:
Для определения радиуса кривизны траектории найдем ее уравнение. Чтобы исключить параметр 
Таким образом, траекторией пальца будет окружность радиусом
Величина нормального ускорения 
Ответ.
Задача №4
Уравнения движения материальной точки имеют вид:
где 
Определить касательное и нормальное ускорение точки.
Решение. Касательное ускорение точки определяется по формуле:
При координатном способе описания движения скорость точки через проекции равна:
Подставим выражение для 

где 

Проекции скорости и ускорения на координатные оси определим по формулам для координатного способа описания движения:
Тогда касательное ускорение точки будет равно:
Для определения нормального ускорения воспользуемся полным ускорением точки, которое уже было найдено, исходя из формул координатного способа описания движения.
Поскольку:
то:
Подставив под корень выражение для 
Ответ.
Задача №5
Точка 


Определить, за какое время скорость точки уменьшится вдвое, и какой путь при этом она пройдет.
Решение. Изобразим траекторию с точкой 
Скорость 


Полное ускорение 


По условию задачи:
где 
Поскольку это равенство должно выполняться и в начальный момент времени 
Откуда:
Таким образом, закон изменения полного ускорения точки под время движения будет иметь вид:
Определим функциональные зависимости от скорости для нормального и касательного ускорений точки:
В уравнении для 
Для определения времени движения и пройденного точкой пути воспользуемся зависимостью для касательного ускорения:
Разделим переменные и проинтегрируем это выражение:
где 
Постоянную интегрирования 
Откуда:
Функциональная зависимость для скорости будет иметь вид:

По условию задачи в конечный момент времени 
Тогда время движения точки будет равно:
Для определения пройденного точкой пути воспользуемся уравнениями:
Разделим переменные и проинтегрируем:
где 
Поскольку в начальный момент 
Таким образом, для пути 
За промежуток времени 
Краткие исторические сведенья про развитие кинематики
Появление первых исследований по кинематике связаны с изобретением огнестрельного оружия. Внимание исследователей привлекали вопросы определения траектории полета снаряда, уточнение понятий о неравномерном и криволинейном движении точки. Леонардо да Винчи (1452 1519) первым изучил вопрос о свободном вертикальном падении тяжелого тела. Но только благодаря трудам Г. Галилея (1564 1642) развитие механики непосредственно связывается с запросами тогдашней техники. Г. Галилей ввел понятие об ускорении и доказал, что траекторией движения снаряда, брошенного в пустоте под некоторым углом к горизонту, является парабола. Законы, установленные Г. Галилеем, нашли свое дальнейшее развитие в трудах Э. Торричелли (1608 1647), который получил формулу для определения скорости падение тела. И. Кеплер (1571 1630) установил кинематические законы движения планет. X. Гюйгенс (1629-1695) впервые обратил внимание на возможность разложения ускорения на касательное и нормальное, строгое доказательство которого дал Л. Эйлер (1707 -1783). Л. Эйлеру принадлежат основополагающие исследования по кинематике точки при естественном способе задания движения, по кинематике вращательного движения твердого тела вокруг неподвижной точки. Развитие кинематики системы точек тесно связано с именем Ж. Лагранжа (1736 1813).
Бурный рост машиностроения в XIX в. способствовал новому развитию кинематики как науки. Глубокие исследования по кинематике твердого тела принадлежат французским ученым М. Шалю (1793 1886), Л. Пуансо (1777 1859), Г. Корюлис (1792 1843). В России основателем научной школы по кинематике механизмов был выдающийся математик П. Л. Чебышев (1821 1894). Его научное наследие в этом направлении разрабатывали советские ученые, среди которых отметим Н. И. Мерцалова (1860 1948), И. И. Артоболевского (1905-1978), А. П. Котельникова (1865-1944), Н. Б. Делоне (1856-1931), Д. С. Зерновая (1860-1922), Л. В. Ассура (1878 1920) и др. Н. Е. Жуковскому (1847-1921) принадлежит много работ по теоретической механике, в том числе и по кинематике, в которых широко используются геометрические методы доказательства различных теорем. Глубокие исследования по кинематике провел В. Н. Лигин (1846-1910).
В XX в. развитие авиации, судостроения, ракетной и космической техники, создание роботов-манипуляторов, гибких автоматизированных производств дали новый толчок в развитии кинематики твердых тел и пространственных механизмов. Исследования связаны с именами А. Н. Крылова, А. Ю. Ишлинского, В. М. Кошлякова, Пола, А. П. Бойчука и др.
Введение в кинематику
Кинематикой называется раздел теоретической механики, в котором изучается движение системы материальных точек с геометрической точки зрения, в частности движение абсолютно твердого тела и материальной точки независимо от действующих на них сил.
Кинематику называют также геометрией движения, поскольку в ней рассматриваются геометрические свойства движения. Кинематика изучает зависимости между пространственно-временными характеристиками механического движения. Механические движения, изучаемые в кинематике, происходят в пространстве и времени. Диалектический материализм рассматривает пространство и время как формы существования материи. «Обе эти формы существования материи без материи являются ничем, пустыми представлениями, абстракциями, что существуют только в нашей голове «. Пространство и время неразрывно связаны между собой, их единство проявляется в движении. В. И. Ленин писал: «В мире нет ничего, кроме движущейся материи, и подвижная материя не может двигаться иначе, чем в пространстве и времени «. Понятие же пространства, времени и движущейся материи в классической механике, основанной на законах Ньютона, формально не связаны друг с другом и являются только первым приближением к реальным объективным формам существования материи, которые позже математически строго установлены теорией относительности.
Отметим, что в теоретической механике пространство, в котором происходит движение тел рассматривается как трехмерное, и все измерения выполняются на основании методов евклидовой геометрии. В теоретической механике время считается одинаковым в любых системах отсчета (системах координат), и не зависит от движения этих систем относительно друг друга. Время обозначается буквой 
Промежутком времени называют течение времени между двумя физическими явлениями.
Моментом времени называют границу между двумя смежными промежутками времени.
Начальным моментом времени называют момент времени, с которого начинается отсчет.
Теория относительности привела к новым представлений о пространстве и времени, которые в значительной степени отличаются от представлений классической механики. Вместе с тем, для случаев движения тела со скоростями, значительно меньше
скорость света, трехмерное евклидово пространство и универсальное время являются полноценными и достаточно точными абстракциями реального времени и реального пространства. Следовательно, можно утверждать, что теоретическое и практическое значение классической механики остается огромным и в наше время, поскольку позволяет найти достаточно высокое приближение к объективно существующих реальным формам
бытия, подтверждается современным развитием техники, в частности космонавтики, робототехники и др.
Изучая движение тела, всегда следует знать, относительно какого другого тела, которое называется телом отсчета, рассматривается это движение. Совокупность тела отсчета, с которым связана система координат, и часов называют системой отсчета. Эта система может быть как подвижной, так и условно неподвижной. Точки тела, которые движутся осуществляют в общем случае различные движения. Поэтому в первую очередь возникает необходимость изучить движение отдельных точек тела.
В кинематике нет разницы, какое движение осуществляет выбрана система координат относительно других тел, не входящих в пределы решаемой задачи, однако всегда следует обращать внимание на то, что характер наблюдательного движения во многом зависит от выбора системы координат. Например, поршень двигателя внутреннего сгорания осуществляет относительно корпуса автомобиля прямолинейное, колебательное движение, а относительно дороги, по которой движется автомобиль с постоянной скоростью, — синусоидальный.
В классической механике постулируется наличие системы отсчета, относительно которой пространство однородно и изотропно, а время -однородно.
В этой системе координат изолированная материальная точка может неограниченно долго
находиться в состоянии покоя или равномерного прямолинейного движения. Такую систему отсчета называют инерциальной. Системы отсчета, не имеющие указанных свойств, называют неинерциальными. Все системы отсчета, находящихся в состоянии покоя или движутся поступательно, равномерно и прямолинейно относительно инерциальной системы отсчета, являются также инерциальными.
Движение геометрического образа тела по отношению к выбранной системы отсчета считается известным, если можно определить его положение относительно этой системы в любой произвольный момент времени. Зависимость параметров, характеризующих положение геометрического образа относительно системы отсчета, от времени определяется соответствующими уравнениями, которые называют законом движения тела.
Поскольку движение геометрического образа тела будет известным, когда будет известен закон движения всех его точек, изучению движения любого геометрического образа, предшествует изучению движения одной его точки. Эта логика лежит в основе разделения кинематики на такие разделы, как кинематика точки, кинематика твердого тела и кинематика совокупности твердых тел и точек.
Три способа задания движения точки
Основной задачей кинематики точки являются изучение зависимости между произвольными положениями подвижной точки в пространстве и времени. Эта зависимость определяет закон движения точки. Закон движения точки считается известным, если можно определить положение точки в пространстве в любой момент времени. Для определения положения точки в пространстве выбирают некоторую систему отсчета (систему координат). Линия, которую описывает точка при своем движении, называется траекторией. Если траектория точки — прямая линия, то движение точки называется прямолинейным, если траектория точки кривая, то — криволинейным. Движение точки относительно выбранной системы отсчета считают заданным, если известно, с помощью какого способа можно определить положение точки в любой момент времени. Основными пространственно-временными (кинематическими) характеристиками движения точки являются ее положение, скорость и ускорение. Исходя из этого, основная задача кинематики точки заключается в нахождении способов задания ее положения и методов определения скорости и ускорение. Движение точки можно определить тремя способами: векторным, координатным и натуральным.
Векторный способ
Положение точки можно определить с помощью радиуса- вектора 



Функцию 


Кривую, которую описывает конец любого вектора при условии, что начало его находится
все время в одной и той же точке, называют годографом вектора. Итак, траектория точки является годографом радиус-вектора 
Координатный способ
Этот способ определения движения точки заключается в том, что задаются координаты точки как функции времени (Рис. 7.1):

Между векторным и координатным способами задания движения существует такая связь:

где 

На том же основании, что и 

Уравнение (7.1) является также уравнением траектории точки в параметрической форме. Исключив из уравнения (7.1) параметр 
Если движение точки задано в полярных координатах (рис. 7.2), то в этом случае следует
задать как функции времени координаты 


где 



В трехмерном пространстве применяются также цилиндрические (рис. 7.3) и сферические
(рис. 7.4) координаты. Уравнения движения точки в цилиндрических координатах имеет вид:

В сферических координатах положение точки определяется полярным радиусом 



Переход от декартовых координат к полярным, цилиндрическим, сферическим и наоборот иметь вид (рис. 7.2-7.4): полярные:

цилиндрические:

сферические:

Отметим, что во всех приведенных тут криволинейных координатах
Натуральный способ
Если траектория точки известна заранее (например, траектория движения поезда, трамвая, троллейбуса и т.п.), то для определения закона ее движения в пространстве достаточно задать положение точки на траектории. Поэтому одну из точек 
Приведенное уравнение определяет закон движения точки по траектории. Функция 





Если движение точки задано координатным способом, то пройденный путь определяется
формулою:

поскольку модуль дифференциала дуги:
Уравнения 




Скорость движения точки
Важной характеристикой движения точки является ее скорость. Понятие скорости точки в
равномерном прямолинейном движении относится к элементарным понятиям.
Движение точки называется равномерным, если приращения радиус-вектора точки за одинаковые промежутки времени будут равными между собой. Для равномерного прямолинейного движения:

где 
промежуток времени 


Рассмотрим теперь неравномерное криволинейное движение точки.
Пусть точка М произвольно движется по некоторой кривой и в момент времени 








Направление вектора 

что средняя скорость лишь приближенно отражает характер истинного движения точки.
Чтобы получить скорость 

Следовательно, скорость точки равна первой производной радиус-вектора точки по времени. За единицу скорости берут 1 м/с. Скорости точки можно дать и другое определение. Скоростью точки в некоторый момент времени t называется физическая величина, которая зависит от времени и позволяет приближенно определить перемещение 


Отсюда, ограничившись величинами первого порядка малость и перейдя к пределу, получим формулу (7.13) для скорости.
Скорость точки в прямоугольной декартовой системе координат
Если движение точки задано координатным способом 

где х, у, z — координаты подвижной точки; 

По определению скорости в соответствии с формулой (7.13) имеем:

Подставив в формулу (7.16) значение 

откуда:

Итак, проекции скорости на оси координат равны первым производным по времени
от соответствующих координат точки.
Модуль скорости:

или

Направление скорости находим по направляющим косинусам:

При движении точки ее скорость в общем случае изменяется во времени. Каждому моменту времени соответствует определенный вектор скорости, направленный по касательной к траектории. Рассмотрим ряд положений точки на траектории, обозначив соответствующие значения ее скорости через 


Зная проекции скорости 
получим в параметрической форме уравнения годографа вектора скорости. Исключив
параметр t из этих уравнений, найдем уравнение годографа вектора скорости в явной форме.
Скорость точки в полярных координатах
Если движение точки в плоскости Оху задано в полярных координатах 

Дифференцируя затем х и у, найдем проекции скорости 

где 

При этом модуль скорости:

Выражение для скорости в полярных координатах можно получить и иначе — введением ортов 
Радиус-вектор 




Для определения производной единичного вектора 





Продифференцировав соотношение (7.26) и учитывая, что 


Воспользовавшись соотношением (7.27), подадим выражение для скорости в виде:

Итак, найдены проекции скорости на радиальное 

Спроектировав их на координатные оси с помощью двух соотношений (7.26), получим выражение (7.23).
Скорость точки при натуральном способе заданный движения
Как уже отмечалось, движение точки является заданным в натуральной форме, если известны ее траектория и закон (уравнения) движения по траектории 



Рассмотрим вектор 

Вектор 

Итак, 
С учетом (7.30) получим следующее выражение для скорости при натуральном способе задания движения точки:

Умножив скалярно обе части выражения (7.31) на орт 




Следовательно, вектор скорости точки при натуральном способе задания движения точки, будет иметь вид:

Если 

Секторная скорость
Секторная скорость 







или
Если ввести вектор 


откуда по определению секторной скорости 


или, с учетом (7.13):

Тогда величина секторной скорости:

Понятие секторной скорости впервые ввел И. Кеплер при выводе второго закона
движения планет вокруг Солнца. Второй закон Кеплера имеет место и при движении искусственных спутников вокруг Земли. Согласно этому закону радиусы-векторы планет, проведенные из центра Солнца, описывают за равные промежутки времени равные площади, то есть скорость есть величина постоянная.
Итак, секторная скорость равна половине векторного произведения радиуса-вектора




Площадь сектора 

где 



Пренебрегая величинами второго порядка малости, последней формуле придадим вид:

Поделив обе части этого равенства на 

Последняя формула выражает секторную скорость в полярных координатах и широко используется в небесной механике и при изучении движения искусственных спутников
Земли.
Ускорение точки
Ускорением точки в инерциальной системе отсчета называют меру изменения скорости точки, которая равны производной скорости этой точки по времени.
Рассмотрим два любых близкие положение точки 














Направление вектора 

Переходя в (7.43) к пределу 


С учетом выражения (7.13) формулу ускорения запишем в виде:

Единицей ускорения в 

Определение ускорения в прямоугольной декартовой системе координат
Если движение точки задано координатным способом, то есть уравнениями 



где 

Откуда:

Итак, проекции ускорения на недвижимые оси координат равны первым производным соответствующих проекций скорости по времени на те же оси, или вторым производным, соответствующих координат подвижной точки по времени.
Модуль ускорения и его направляющие косинусы запишем в виде:


Ускорение точки в полярных координатах
Пусть движение точки М в плоскости Оху задано в полярных координатах
(рис. 7.15). Декартовые координаты выражаются через полярные по формулам









Учитывая зависимость между полярными и декартовыми координатами, получим:

Сравнивая соответствующие выражения для 


Модуль ускорения определим по формуле:

Обозначив через 




Заметим, что формулы (7.53) можно также получить непосредственным дифференцированием выражения (7.28) для скорости 
Ускорение точки при натуральном способе задания движения
Предварительно приведем некоторые сведения из дифференциальной геометрии.
Натуральные оси и натуральный трехгранник. Кинематические характеристики движения точки тесно связаны с геометрическими свойствами траектории. Как известно из дифференциальной геометрии, в каждой точке кривой есть три взаимно перпендикулярных направления: касательная, главная нормаль и бинормаль, единичные вектора (или орты) которых обозначим соответственно 





Итак, натуральные оси — это подвижные оси, связанные с подвижной точкой М, образующие правую прямоугольную систему координат (натуральный трехгранник) (рис. 7.16). Плоскость, проходящая через главную нормаль 





Кривизна кривой. Угол, образует дугу 







Предел этого отношения при 


В общем случае кривизна кривой не является постоянной величиной и изменяется от точки
к точке. Величина 
кривизны кривой в этой точке:

Очевидно, что:

Ускорение точки при натуральном способе задания движения определяется по теореме.
Теорема. Полное ускорение точки равно векторной сумме касательного (тангенциального) и нормального ускорений.
Доказательство. Пусть движение точки задано натуральным способом. Тогда вектор скорости подадим в виде (7.33). Учитывая это и соблюдая определения ускорения при векторном способе задания движения точки, получим:

Первое слагаемое является вектором, направленным по касательной 


Как следует из (7.61), касательное ускорение характеризует изменение скорости по величине и равно первой производной от проекции скорости на касательную или второй производной от дуговой координаты по времени. Чтобы определить второе слагаемое, представим его в виде:

Рассмотрим предварительно тождество 





соприкасающихся плоскостях, то вектор 


Определим теперь модуль вектора 



Следовательно:

Таким образом, с учетом (7.62) и (7.63) второе слагаемое выражения (7.60) будет выглядеть так:
и называется нормальным ускорением и обозначается 

Отсюда следует, что нормальное ускорение 
Поскольку составляющие вектора 





что и нужно было доказать.
Модуль полного ускорения:

Направление вектора 


Если движение точки задано координатным способом, то, воспользовавшись выражениями (7.64) и (7.66), нетрудно получить следующее выражение для радиуса кривизны:

Заметим так же, что выражение (7.61) для касательного ускорения, можно представить в таком виде:
С учетом последнего выражения (7.67) для радиуса кривизны можно записать так:

В случае плоского движения, когда 


Если движение задано в полярной системе координат, то можно убедиться, что формулу для кривизны траектории можно записать в виде:

Приведем еще формулу для радиуса кривизны в случае, когда уравнение плоской кривой задано в явной форме

В завершении приведем формулы Френе, которые дают возможность установить связь между ортами 

В параграфе 7.7. выражение (7.30) (рис. 7.12) дает соотношение:
Из последней формулы и выражения (7.63) получим:
Поскольку бинормаль 


Приведенные соотношения и являются формулами Френе.
Отдельные случаи движения точки
Прямолинейное движение. Если во время движения точки нормальное ускорение 



Если при криволинейном движении точки в данный момент времени нормальное ускорение равна нулю 
Равномерное криволинейное движение. Если во время движения точки касательное ускорение равна нулю 


Равномерное прямолинейное движение. Если во время движения точки ее ускорение равно нулю 
Равнопеременное криволинейное движение. Если во время движения точки по некоторой кривой, касательное ускорение будет постоянным по величине 


Найдем скорость и закон движения точки 





Поскольку 

Постоянную интегрирования 


Прямолинейные гармонические колебания точки. Пусть точка движется по прямой, например по оси Ох, и ее расстояние от начала координат меняется по закону:

где 
Движение точки является колебательным между положениями точки 






Пример 1. Найти уравнение траектории, скорость, ускорение и радиус кривизны в момент 
Решение. Уравнение траектории задается в параметрической форме Исключив параметр 

Итак, траекторией точки будет эллипс с полуосями 
Определим модули и направления скорости и ускорения:
При
Аналогично
При 
Радиус кривизны определяется по формуле (7.67):

При
Пример 2. Точка движется по кругу радиусом 

в момент времени
Решение. Поскольку движение точки задано натуральным способом, то скорости точки определяются в виде 



Полное ускорение точки
Пример 3. По заданным уравнениям движения точки найти ее траекторию, скорость, ускорение и радиус кривизны.
Решение. Для нахождения траектории точки возведем х и у в квадрат и добавим их,
тогда получим
Для нахождения скорости и ускорения вычислим сначала их проекции на оси:
Теперь легко вычислить величины скорости и ускорения:
Траектория точки показана на рис. 7.18. Очевидно, что радиус кривизны равен радиусу окружности 

Убедимся в этом с помощью формул. Используем формулу (7.70). В этом случае:

Пример 4. Движимое колесо радиусом 
кривошипа ОА внутри неподвижного колеса радиусом R. Составить уравнение траектории точки М подвижного колеса. Для частного случая 

Решение. Расположим в точке О начало неподвижных осей 

мгновенное значение угла между кривошипом ОА и осью Ох. Поскольку по условиям задачи качения происходит без скольжения, то дуги ВС и CM должны быть равными. Таким образом,

где 
Отметим, что кривошип ОА и движимое колесо вращаются в противоположных направлениях.
Обозначив через 


Подставив в (2) из (1) выражение 

Уравнение (3) представляют собой в параметрической форме уравнения гипоциклоида — кривой, описываемой точкой окружности, катящейся без скольжения внутри второго круга.
Дальнейшее исследование нужно провести для случае 



Дальше получим:
Следовательно, 



Криволинейные координаты. Коэффициенты Ламе
Криволинейными координатами точки называется система независимых параметров, однозначно определяющих ее положение. Обозначим криволинейные координаты через 


Уравнения движения точки в криволинейных координатах будут выглядеть так:

Эти функции должны быть непрерывными и однозначными и хотя бы дважды дифференцируемыми. Пусть радиус-вектор, определяющий положение точки М, которая задана координатами 

Проекции радиус-вектора на оси декартовой системы координат также являются функциями 

Если в функциях (7.75) только одна координата 


Аналогично определяются координатные линии, соответствующие изменению 

В каждой точке пространства пересекаются три координатные линии, касательные к которым в указанной точке, проведенные в сторону увеличения координат, называются координатными осями 
Если в уравнениях (7.75) менять две координаты при фиксированной третий, то полученные поверхности называются координатными. Уравнение координатных поверхностей имеют вид:

Каждое из этих уравнений определяет в соответствии поверхности 
Определим теперь орты 

времени t точка находится в положении 

направленный по касательной к координатной линии 


то
Отсюда единичный вектор
Аналогично можно получить формулы для 



где

Как видно из формул (7.79), 

называются коэффициентами Ламе или дифференциальными параметрами Ламе.
Применяя формулы (7.78), можно определить косинусы криволинейных координатных осей с осями декартовых координат. Действительно, введя единичные вектора декартовых координатных осей 

Будем рассматривать только ортогональные криволинейные координаты, координатные оси которых взаимно перпендикулярны. Условиями ортогональности является равенство нулю скалярных произведений единичных векторов, то есть 

Покажем, что коэффициенты Ламе являются множителями при дифференциалах координат в выражениях дифференциалов дуг соответствующих координатных линий. Действительно, найдем формулу, по которой определяется дифференциал дуг кривой в системе ортогональных координат. Для этого сначала определим элементарное перемещение:

Тогда
или, учитывая ортогональность криволинейных координат (7.81), получим:

поскольку 
На основании полученной формулы легко перейти к определению коэффициентов Ламе. Получим:

Последние выражения можно получить, поочередно предполагая изменение только одной криволинейной координаты и считая две другие фиксированными.
Пример 5. Определить коэффициенты Ламе, если движение точки задано в цилиндрической (рис. 7.3)

Решение. В цилиндрической системе координат получим:
Следовательно, 

Скорость и ускорение точки в криволинейных координатах
На основании (7.13) и с учетом зависимости (7.74) получим следующее выражение для скорости в криволинейных координатах:

Из формулы (7.78) получим
С учетом этих соотношений получим

Это равенство можно рассматривать как разложение скорости по единичным ортах осей
криволинейной системы координат, то есть:

Поскольку рассматривается случай ортогональной криволинейной системы координат,
то модуль скорости находим по формуле:

Для определения ускорения точки в криволинейных координатах найдем сначала проекции вектора ускорения на координатные оси, учитывая соотношение (7.78):

Не тяжело убедиться, что правую часть этих равенств можно представить в виде:

Для дальнейшего преобразования формулы (7.90) получим очевидные тождества, которые вытекают из выражений (7.86) и (7.78):
или

Продифференцировав по времени выражение 

Определив затем из выражения (7.85) частные производные 

Подставив в (7.90) значение 


Преобразуем дальше скалярные произведения 


Подставив соотношения (7.95) в (7.94), найдем проекции ускорений точки на оси криволинейной системы координат:

Введем сокращенное обозначение, согласно (7.88),

окончательно получим:

Отметим, что как будет показано в динамике, выражение 

Пример 6. Движение точки задано в цилиндрической системе координат 
Решение. Учитывая связь декартовых координат с цилиндрическими, получим




откуда
Затем определим ускорение точки. Для этого составив выражение для функции:
Вычислим 

Теперь по формуле (7.98) найдем проекции ускорения на оси заданной криволинейной системы координат:
Пример 7. Найти выражения для скорости и ускорение точки, движение которой задано в сферической системе координат (рис. 7.4).
Решение. Криволинейными координатами в этом случае является
которые связаны следующими соотношениями с декартовыми:
Для выражения коэффициентов Ламе, воспользуемся выражениями (7.79). Для этого найдем сначала частные производные
Подставив эти производные в формулы (7.79), получим:

Дальше по формуле (7.87) получим:

Для нахождения соответствующих проекций ускорения вычислим сначала вспомогательную функцию 

Проведем вспомогательные вычисления согласно операциям формулы (7.98):

Подставив выражения (4) в (7.98), получим:


Выражения (2) и (5) будут решениями этой задачи.
Пример 8. Самолет, который принято за точку, движется относительно земной поверхности, которая принята за сферу радиусом R со скоростью на заданной высоте h так, что ее северная и восточная составляющие соответственно равны 

Решение. Отметим, что ортогональная система криволинейных координат 

Поскольку самолет летит на одной высоте, то очевидно, что 

Пример 9. При условиях задачи 8 найти ускорение самолета относительно неподвижной системы координат 
Решение. С рис. 7.23 видим, что вращение Земли даст дополнительно две составляющие угловые скорости
Что касается угловых скоростей, которые характеризуются криволинейными координатами


поэтому угловые скорости, характеризующих изменения координат 


где 

Итак, для вычисления ускорения самолета в неподвижной системе координат с учетом суточного вращения Земли нужно в формулу примера 7 подставить значение 




Выражения (3) и (4) и будут решением задачи.
Основные понятия кинематики
Кинематика изучает движение материальных объектов как моделей реальных тел (точка, твердое тело, материальная система) с геометрической точки зрения, как геометрических образов, без изложения причин, вызывающих это движение. Такой подход не требует учета инерционных и силовых характеристик: масса и момент инерции, сила и момент силы.
Движение является формой существования материального мира, а механическое движение, простейшая форма движения материи — один из результатов взаимодействия материальных тел. Под ним понимают изменение положения тел в пространстве в течении времени по отношению к другому телу, с которым связана система отсчета.
Пространство, в котором происходит движение геометрических моделей в форме
перечисленных материальных объектов, считается абсолютным, метрические
особенности которого независимы от движения в нем материи в разных точках и
направлениях (однородность и изотропность пространства). Такое пространство
воспринимается как трехмерное, так что каждой точке абсолютного пространства
соответствуют, например, в декартовой системе, три координаты. Единицей измерения пространства в Международной системе единиц СИ является метр (1 м). 1 метр — это
млн. часть длины земного меридиана.
Свойство абсолютного времени — однородность и универсальность, оно одинаково всплывает во всех точках пространства, на всех телах. Поэтому можно
произвольно выбирать начало отсчета времени и измерять интервалы между
отдельными промежутками или моментами времени. Единицей измерения времени является секунда (1 с). 1 секунда — это 
Под абсолютным пространством и временем вводится понятие системы отсчета. Это совокупность системы координат, неизменно связанной с некоторым телом отсчета, и устройством с периодическим процессом для измерения времени (часы).
Во множественном числе систем отсчета, в которых можно постулировать пространство и время как абсолютные, выбираются так называемые инерциальные системы отсчета, в которых изолированная материальная точка может неограниченно долго находиться в состоянии покоя или равномерного и прямолинейного движения под действием системы
уравновешенных сил.
Если некоторая система отсчета служит за инерциальную с заданной степенью точности, то можно указать бесконечное количество инерциальных систем отсчета, движущихся относительно выбранной системы поступательно, равномерно и прямолинейно.
При решении задач небесной механики, исчислении траекторий спутников принимается гелиоцентрическая система отсчета с началом в центре масс Солнечной системы и осями координат, направленными на неподвижные звезды.
При решении многих технических задач по инерциальную принимают за систему отсчета, связанную с центром Земли (геоцентрическая система отсчета).
Движение геометрической модели относительно выбранной системы отсчета считается известным, если можно определить его положение относительно этой системы в любой момент времени. При этом различают момент времени и промежуток времени. Промежуток времени — это течение времени между двумя физическими явлениями. Момент времени — это граница между двумя смежными промежутками времени.
Положение модели относительно данной системы отсчета определяется
соответствующими параметрами, а ее движение — кинематическими уравнениями,
выражают изменение этих параметров как функций времени.
Основная задача кинематики заключается в том, чтобы по известным кинематическим уравнениям движения определить кинематические характеристики этого движения: траектории точек, их линейные скорости и ускорения; угловые скорости и ускорения тела.
Поскольку каждое тело состоит из материальных точек, то естественно начать кинематику по изучению движения материальной точки.
Кинематика материальной точки
Для того, чтобы изучать движение материальной точки, необходимо выбрать способ его задания. Существует несколько способов задания движения материальной точки.
Кинематически задать движение или закон движения точки значит указать такой способ, позволяющий определить положение этой точки относительно данной системы отсчета в любой момент времени.
Способы задания движения материальной точки
Для задания движения материальной точки можно применить один из трех следующих способов:
1. Векторный;
2. Координатный;
3. Натуральный.
Рассмотрим последовательно указанные способы.
Векторный способ задания движения материальной точки
Этот способ нашел широкое применение в теоретических расчетах. Рассмотрим сущность этого способа.
Предположим, что произвольная материальная точка M движется в пространстве по некоторой траектории AB (рис. 2.1). Возьмем в пространстве прямоугольную декартову систему координат Oxyz с единичными векторами (ортами) на соответствующих осях 







где t — время.
Соотношение называется кинематическим уравнением движения материальной точки в векторной форме. Одновременно это выражение можно рассматривать как уравнение траектории движения.
Найдем в принятой системе координат Oxyz величину радиус-вектора 




где x(t), y(t), z(t) — текущие значения координат конца радиус-вектора 
Определим кинематические характеристики подвижной точки М.
Траектория движения точки
Траекторией АВ движения материальной точки М является геометрическое место концов радиус-вектора 
Введем понятие годографа векторной функции 




Скорость движения точки
Вторая кинематическая характеристика — скорость движения материальной точки M, показывает, как быстро и в каком направлении меняется ее положение в пространстве.
Скорость — это векторная величина, характеризующая степень изменения перемещения по времени.
Единица измерения скорости — 

Для определения этой кинематической характеристики рассмотрим движение
материальной точки М. Считаем, что точка М движется по произвольной траектории АВ (рис. 2.1). За некоторый промежуток времени ∆t точка переместилась из положения М в положение M1 (радиус-вектор 



По направлению вектор 

Если рассмотреть границу средней скорости 
Таким образом, при векторном способе задания движения материальной точки ее скорость является первой производной от радиус-вектора точки по времени.
Направление вектора скорости 
Ускорение движения точки
Третья кинематическая характеристика — ускорение движения материальной точки M, показывает, как быстро и в каком направлении меняется ее скорость движения.
Ускорение — это векторная величина, характеризующая степень изменения вектора скорости по времени.
Единица измерения ускорения — 
Определим ускорение материальной точки M. Рассмотрим движение точки по произвольной траектории AB (рис. 2.2). В положении М скорость точки была 







Вектор 

Для получения мгновенного ускорения материальной точки необходимо рассмотреть бесконечно малый промежуток времени (то есть ∆t → 0), а все выражение свести к границе:
Если подставить в значение скорости точки уравнение выше, то будем иметь:
Таким образом, при векторном способе задания движения материальной точки ее ускорение равно первой производной от скорости движения точки по времени, или второй производной от радиус-вектора точки по времени.
Вектор ускорения 
Координатный способ задания движения материальной точки
Этот способ задания движения материальной точки широко используется при решении задач, в технических расчетах.
При таком способе задания движения материальной точки заранее задаются координаты материальной точки как функции времени. Если выбрать в пространстве прямоугольную декартову систему координат Oxyz, то при движении точки M все три ее координаты будут меняться со временем (рис. 2.1). Для того, чтобы знать положение точки в любой момент времени, а также для определения ее кинематических характеристик, необходимо задать выражения этих координат как функции времени:
x = x(t),
y = y(t),
z = z(t).
Эти параметрические уравнения, в которых роль параметра играет время t, является
кинематическими уравнениями движения точки в прямоугольной декартовой системе
координат (или законом движения точки в координатной форме) и определяют суть данного способа.
Следует заметить, что если движение материальной точки осуществляется в одной плоскости xOy, то в уравнениях закон изменения координаты z уже не нужен и уравнение приобретает следующий вид:
x = x(t),
y = y(t),
Если материальная точка совершает прямолинейное движение, то достаточно выбрать одну ось координат, например Ox, совместив ее с направлением движения, тогда это движение будет описано одним уравнением:
x = x(t).
Определим кинематические характеристики движения материальной точки при данном способе задания ее движения.
Траектория движения точки
Уравнения выше фактически являются уравнениями траектории движения материальной точки в параметрической форме, в которых, как было сказано выше, роль параметра играет время t. Для нахождения траектории движения в обычной форме необходимо исключить из уравнений движения время t, то есть получить зависимость между самими координатами. Это можно сделать несколькими способами. Например, подстановкой или подъемом обеих частей уравнений квадрату и почленно добавлением (если уравнения содержат тригонометрические функции).
Пример:
Движение материальной точки осуществляется в плоскости xOy и заданный такими уравнениями:
x = 2t, м,
y = 12t2, м,
Определить траекторию движения точки.
Решение.
Траекторию движения материальной точки можно определить одним из двух способов:
а) задать разные моменты времени и изобразить координаты точки х, у на графике;
б) исключить время t из заданных уравнений движения. Так, из первого уравнения время будет равняться t = 
y = 
Таким образом, траектории движения точки является парабола с вершиной, которая
расположена в начале координат и осью симметрии yO.
Пример:
Движение материальной точки задано уравнениями:
x = 3sin t см,
y = 3cos t см,
где t — в секундах.
Определить траекторию движения точки.
Решение.
Уравнение траектории движения можно определить, если исключить время t с уравнений движения. Перепишем уравнение движения материальной точки следующим образом:
Поднося к квадрату и добавляя отдельно левые и правые части этих выражений, получим:
или
x2 + y2 = 32.
Итак, уравнением траектории движения материальной точки будет уравнения
окружности радиусом R = 3 см с центром в начале координат.
Скорость движения точки
Для определения скорости движения материальной точки при координатном способе задания используем основные положения, которые были полученные при рассмотрении векторного способа задания движения материальной точки. С этой целью, подставив выражение в выражение, получим:
С другой стороны, вектор скорости 
где vx, vy, и vz — проекции вектора скорости на соответствующие оси координат.
Если рассмотреть и сравнить выражения, то можно увидеть, что есть возможность приравнять коэффициенты при единичных векторах 


Таким образом, проекции вектора скорости материальной точки на координатные оси равны первым производным по времени от соответствующих координат.
Если известны проекции вектора скорости на оси координат, то есть возможность составить их геометрически и получить модуль вектора скорости v материальной точки:
Направление вектора скорости 
Зная направляющие косинусы, через арккосинус находят сами углы.
Ускорение движения точки
Для определения ускорения движения материальной точки при координатном способе задания движения ведем себя аналогично, как и в случае определения скорости движения. А именно: значение радиус-вектора 
С другой стороны, вектор ускорения 
Если сравнить уравнения, то можно написать такие соотношения:
Таким образом, проекции вектора ускорения материальной точки на оси координат равны вторым производным по времени от соответствующих координат.
Если известны проекции вектора ускорения на оси координат, то есть возможность составить их геометрически и получить модуль самого вектора:
a = 
Направление вектора 
Используя значение направляющих косинусов, через арккосинус находят сами углы.
Таким образом, при координатном способе задания движения материальной точки, если это движение осуществляется в пространстве, ее скорость 

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Ускорение и его составляющие
В случае неравномерного движения важно
знать, как быстро изменяется скорость
с течением времени. Физической величиной,
характеризующей быстроту изменения
скорости по модулю и направлению,
является ускорение.
Рассмотрим плоское движение, т.е.
движение, при котором все участки
траектории точки лежат в одной плоскости.
Пусть вектор v задает скорость точки А
в момент времени t.
За время t
движущаяся точка перешла в положение
В и приобрела скорость, отличную от
v как по модулю, так и
направлению и равную v1
= v + v.
Перенесем вектор v1
в точку А и найдем v
(рис. 4).
Средним ускорением неравномерного
движения в интервале от t
до t + t
называется векторная величина, равная
отношению изменения скорости v
к интервалу времени t
Мгновенным ускорением а (ускорением)
материальной точки в момент времени
t будет предел среднего
ускорения:
Таким образом, ускорение a
есть векторная величина, равная первой
производной скорости по времени.
Разложим вектор v
на две составляющие. Для этого из точки
А (рис. 4) по направлению скорости v
отложим вектор
,
по модулю равный v1.
Очевидно, что вектор
,
равный
,
определяет изменение скорости за время
t
по модулю:
.
Вторая же составляющая
вектора v
характеризует изменение скорости
за время t
по направлению.
-
Тангенциальное и нормальное ускорение.
Тангенциа́льное
ускоре́ние
— компонента ускорения, направленная
по касательной к траектории движения.
Совпадает с направлением вектора
скорости при ускоренном движении и
противоположно направлено при замедленном.
Характеризует изменение модуля скорости.
Обозначается обычно или (, итд в
соответствии с тем, какая буква выбрана
для обозначения ускорения вообще в
данном тексте).
Иногда
под тангенциальным ускорением понимают
проекцию вектора тангенциального
ускорения — как он определен выше — на
единичный вектор касательной к траектории,
что совпадает с проекцией (полного)
вектора ускорения на единичный вектор
касательной то есть соответствующий
коэффициент разложения по сопутствующему
базису. В этом случае используется не
векторное обозначение, а «скалярное»
— как обычно для проекции или координаты
вектора —
.
Величину
тангенциального ускорения — в смысле
проекции вектора ускорения на единичный
касательный вектор траектории — можно
выразить так:
где
— путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
Если
использовать для единичного касательного
вектора обозначение
,
то можно записать тангенциальное
ускорение в векторном виде:
Вывод
Выражение
для тангенциального ускорения можно
найти, продифференцировав по времени
вектор скорости, представленный в виде
через единичный вектор касательной
:
где
первое слагаемое — тангенциальное
ускорение, а второе — нормальное
ускорение.
Здесь
использовано обозначение
для единичного вектора нормали к
траектории и
— для текущей длины траектории (
);
в последнем переходе также использовано
очевидное
и,
из геометрических соображений,
Центростремительное
ускорение(нормальное) —
часть полного ускорения точки,
обусловленного кривизной траектории
и скоростью движения по ней материальной
точки. Такое ускорение направлено к
центру кривизны траектории, чем и
обусловлен термин. Формально и по
существу термин центростремительное
ускорение в целом совпадает с термином
нормальное ускорение, различаясь скорее
лишь стилистически (иногда исторически).
Особенно
часто о центростремительном ускорении
говорят, когда речь идет о равномерном
движении по окружности или при движении,
более или менее приближенном к этому
частному случаю.
Элементарная
формула
или
где
— нормальное (центростремительное)
ускорение,
— (мгновенная) линейная скорость движения
по траектории,
— (мгновенная) угловая скорость этого
движения относительно центра кривизны
траектории,
— радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая ).
Выражения
выше включают абсолютные величины. Их
легко записать в векторном виде, домножив
на — единичный вектор от центра кривизны
траектории к данной ее точки:
Эти
формулы равно применимы к случаю движения
с постоянной (по абсолютной величине)
скоростью, так и к произвольному случаю.
Однако во втором надо иметь в виду, что
центростремительное ускорение не есть
полный вектор ускорения, а лишь его
составляющая, перпендикулярная траектории
(или, что то же, перпендикулярная вектору
мгновенной скорости); в полный же вектор
ускорения тогда входит еще и тангенциальная
составляющая (тангенциальное ускорение)
,
по направлению совпадающее с касательной
к траектории (или, что то же, с мгновенной
скоростью).
вывод
То,
что разложение вектора ускорения на
компоненты — одну вдоль касательного
к траектории вектора (тангенциальное
ускорение) и другую ортогональную ему
(нормальное ускорение) — может быть
удобным и полезным, довольно очевидно
само по себе. Это усугубляется тем, что
при движении с постоянной по величине
скоростью тангенциальная составляющая
будет равной нулю, то есть в этом важном
частном случае остается только нормальная
составляющая. Кроме того, как можно
увидеть ниже, каждая из этих составляющих
имеет ярко выраженные собственные
свойства и структуру, и нормальное
ускорение содержит в структуре своей
формулы достаточно важное и нетривиальное
геометрическое наполнение. Не говоря
уже о важном частном случае движения
по окружности (который, к тому же,
практически без изменения может быть
обобщен и на общий случай).
Формальный
вывод
Разложение
ускорения на тангенциальную и нормальную
компоненты (вторая из которых и есть
центростремительное или нормальное
ускорение) можно найти, продифференцировав
по времени вектор скорости, представленнный
в виде
через единичный вектор касательной
.
Где
первое слагаемое — тангенциальное
ускорение, а второе — нормальное
ускорение.
Здесь
использовано обозначение
для единичного вектора нормали к
траектории и —
для
текущей
длины траектории (
);
в последнем переходе также использовано
очевидное
.
Далее
можно просто формально назвать член
—
нормальным
(центростремительным) ускорением. При
этом его смысл, смысл входящих в него
объектов, а также доказательство того
факта, что он действительно ортогонален
касательному вектору (то есть что —
действительно вектор нормали) — будет
следовать из геометрических соображений
(впрочем, то, что производная любого
вектора постоянной длины по времени
перпендикулярна самому этому вектору,
— достаточно простой факт; в данном
случае мы применяем это утверждение
для ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

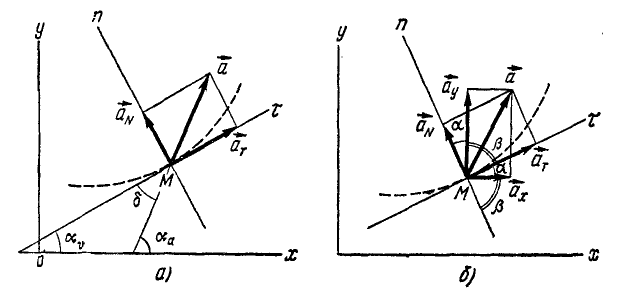
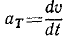
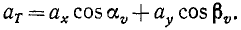
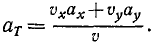
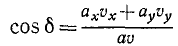
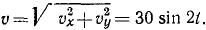
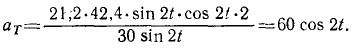
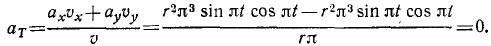
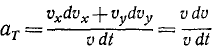
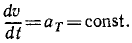
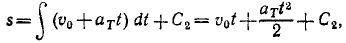
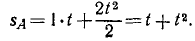
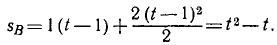
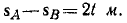
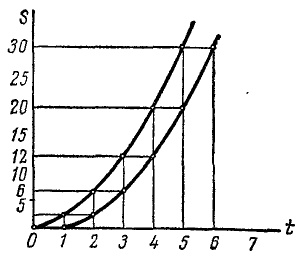
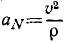
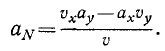
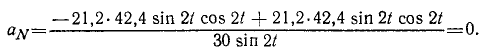
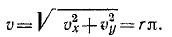
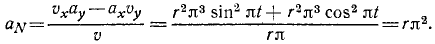
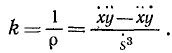
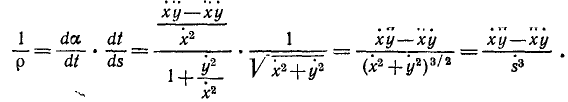
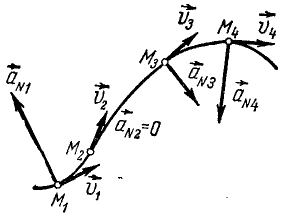
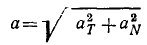
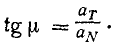
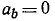
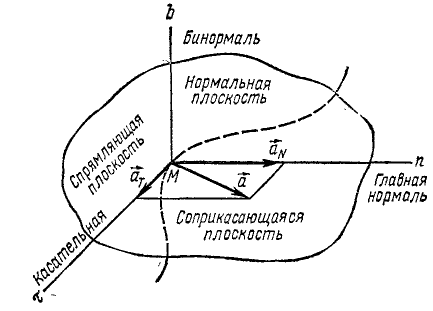
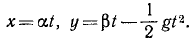
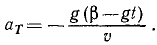
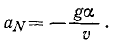
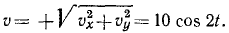
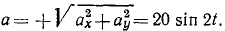
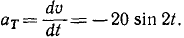
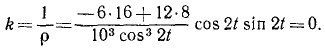
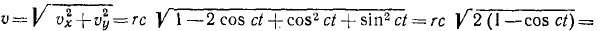
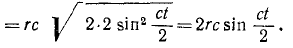
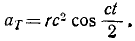
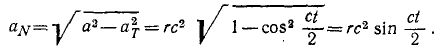
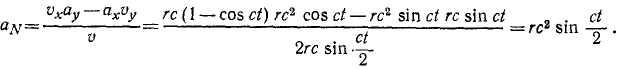
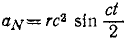
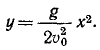
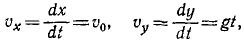
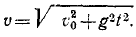
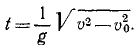
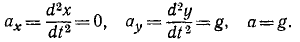
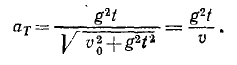
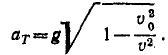
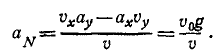
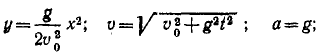
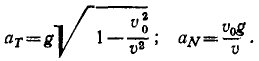
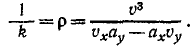
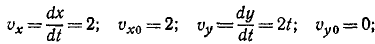
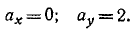
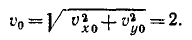
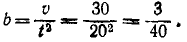
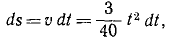
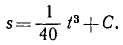
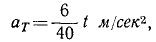
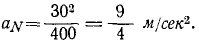
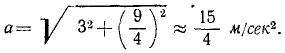
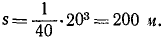














































































































































































































































































































 (рис.1.5) .
(рис.1.5) . как начало отсчета дуги и положительное направление вдоль траектории (на рис. 1.5 слева направо).
как начало отсчета дуги и положительное направление вдоль траектории (на рис. 1.5 слева направо). , которую берут с соответствующим знаком. При движении точки по траектории каждому моменту времени
, которую берут с соответствующим знаком. При движении точки по траектории каждому моменту времени 





































































































































































































































