Как найти тангенс 765 градусов

Примеры:

(tg⁡:30^° =frac{1}{sqrt{3}})
(tg⁡:(frac{π}{3})=sqrt{3})
(tg:⁡2=-2,185…)

Содержание:

• Аргумент и значение
• 
  Тангенс острого угла
• 
  Тангенс числа или любого угла
• 
  Знаки по четвертям
• 
  Связь с другими функциями

Аргумент и значение тангенса

Аргументом тангенса может быть:
— как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.

Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).

Значение тангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)

Тангенс острого угла

Пример:

1) Пусть дан угол и нужно определить тагенс этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить тангенс.

Вычисление тангенса числа или любого угла

Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга:

Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:⁡0=0). Получается: (tg:0=)(frac{sin:⁡0}{cos:⁡0}) (=)(frac{0}{1})(=0).

Ответ: (0).

Пример. Вычислите (tg:(-765^circ)).
Решение:   (tg: (-765^circ)=)(frac{sin:(-⁡765^circ)}{cos:⁡(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin⁡(-765^°)=-frac{sqrt{2}}{2});
(cos⁡(-765^°)=frac{sqrt{2}}{2}) ;
получается (tg(-765^°)= -frac{sqrt{2}}{2} ∶ frac{sqrt{2}}{2}=-1).

Ответ: (-1).

Пример. Вычислите (tg:frac{π}{3}).
Решение:   (tg: frac{π}{3}=)(frac{sin:⁡frac{π}{3}}{cos:⁡frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin⁡(frac{π}{3})=frac{sqrt{3}}{2});
(cos⁡(frac{π}{3})=frac{1}{2}) ;
получается (tg(frac{π}{3})= frac{sqrt{3}}{2} ∶ frac{1}{2}= frac{sqrt{3}}{2} cdot frac{2}{1}=sqrt{3}).

Ответ: (sqrt{3}).

Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.

Пример. Вычислите (tg:frac{π}{4}).
Решение:   
1)Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).

Ответ: (1).

Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:   
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt{3}) (приблизительно (-1,73)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-)(frac{7π}{2}),(-)(frac{3π}{2}),(frac{π}{2}), (frac{5π}{2}), (frac{9π}{2}) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-)(frac{9π}{2}),(-)(frac{5π}{2}),(-)(frac{π}{2}), (frac{3π}{2}), (frac{7π}{2}) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .

Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).

Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ.

Знаки по четвертям

С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.

Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:

— косинусом того же угла: формулой (1+tg^2⁡x=)(frac{1}{cos^2⁡x}) 

— синусом и косинусом того же угла: (tg⁡:x=)(frac{sin:⁡x}{cos⁡:x}) 

— котангенсом того же угла: формулой (ctg⁡:x=)(frac{1}{tg:x}) 
Другие наиболее часто применяемые формулы смотри здесь.

Смотрите также:
Формулы приведения

Задания

Версия для печати и копирования в MS Word

tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.

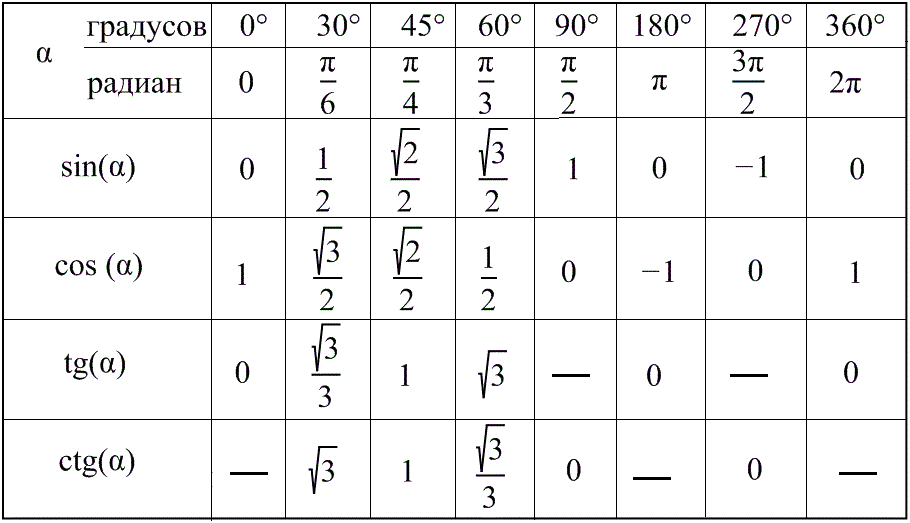
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций

Доп. Инфо:

1. Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
2. Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
3. Таблица синусов, она-же косинусов точная.
4. Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
5. Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
6. Таблица тангенсов, она же котангенсов точная.
7. Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
   Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
8. Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
9. Определение и численные соотношения между единицами измерения углов в РФ.
   Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
10. Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.

Задача 30156 Найдите значение выражения -17tg765°. …